The Structure of the Parallel Electric Field and

The Structure of the Parallel Electric Field and Particle Acceleration During Magnetic Reconnection • J. F. Drake • M. Swisdak • M. Shay University of Maryland • M. Hesse GSFC • C. Cattell University of Minnesota

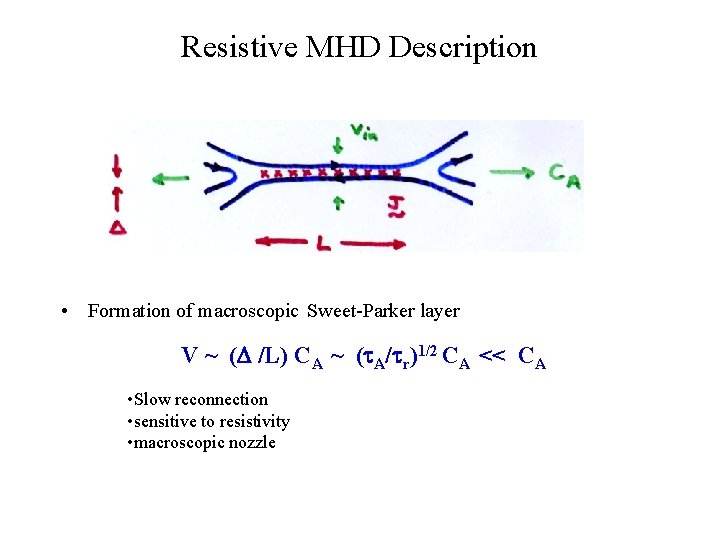
Resistive MHD Description • Formation of macroscopic Sweet-Parker layer V ~ ( /L) CA ~ ( A/ r)1/2 CA << CA • Slow reconnection • sensitive to resistivity • macroscopic nozzle

Overview • MHD model yields reconnection rates to low to explain observations in nature – solar flares – sawtooth crash – magnetospheric substorms • Non-MHD physics at small spatial scales produces fast reconnection – Focus on reconnection with a guide field and the coupling to dispersive kinetic Alfven waves – Structure of the parallel electric field • Some form of anomalous resistivity is often invoked to explain discrepancies – strong electron-ion streaming near x-line drives turbulence and associated enhanced electron-ion drag – Parallel electric field develops structure in the form of electron holes and double layers – Observational evidence in from recent Cluster data

Generalized Ohm’s Law • Electron equation of motion c/ pe Electron inertia c/ pi whistler waves • MHD valid at large scales • Below c/ pi or s electron and ion motion decouple • electrons frozen-in • whistler and kinetic Alfven waves control dynamics • Electron frozen-in condition broken below c/ pe • Non-gyrotropic pressure tensor dominates s kinetic Alfven waves scales

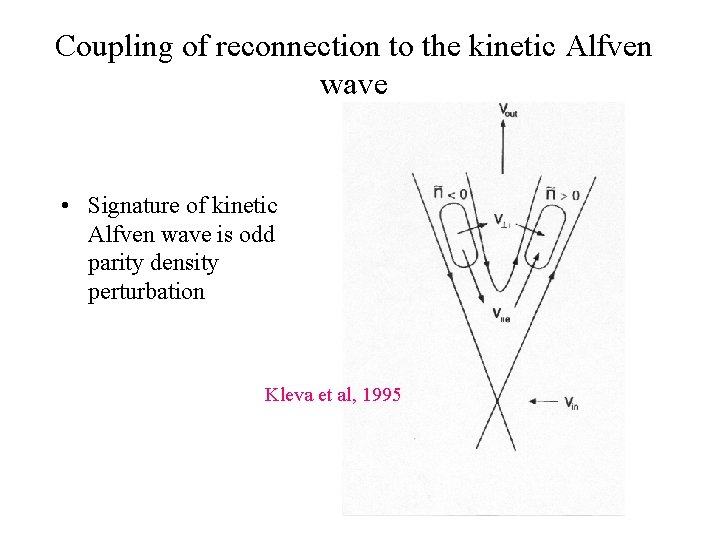
Coupling of reconnection to the kinetic Alfven wave • Signature of kinetic Alfven wave is odd parity density perturbation Kleva et al, 1995

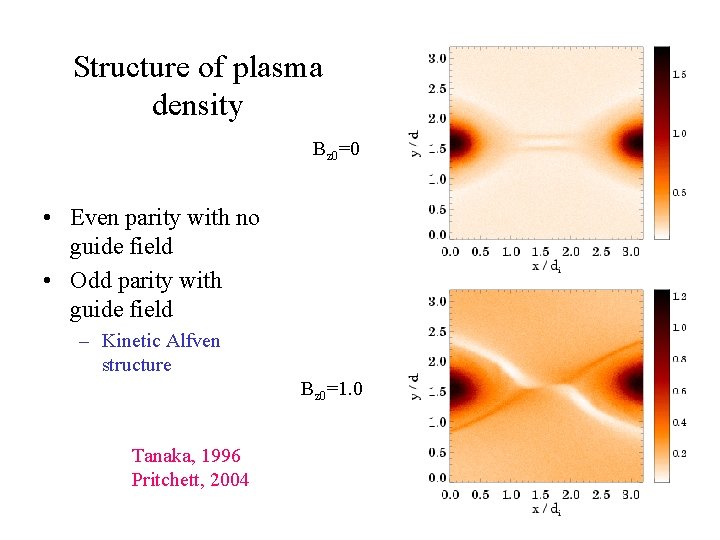
Structure of plasma density Bz 0=0 • Even parity with no guide field • Odd parity with guide field – Kinetic Alfven structure Bz 0=1. 0 Tanaka, 1996 Pritchett, 2004

Conditions for Dispersive waves • Geometry • whistler = = • kinetic Alfven =

Parameter space for dispersive waves • Parameters • For sufficiently large guide field have slow reconnection Rogers, et al, 2001 none kinetic Alfven 1 whistler kinetic Alfven whistler 1 y

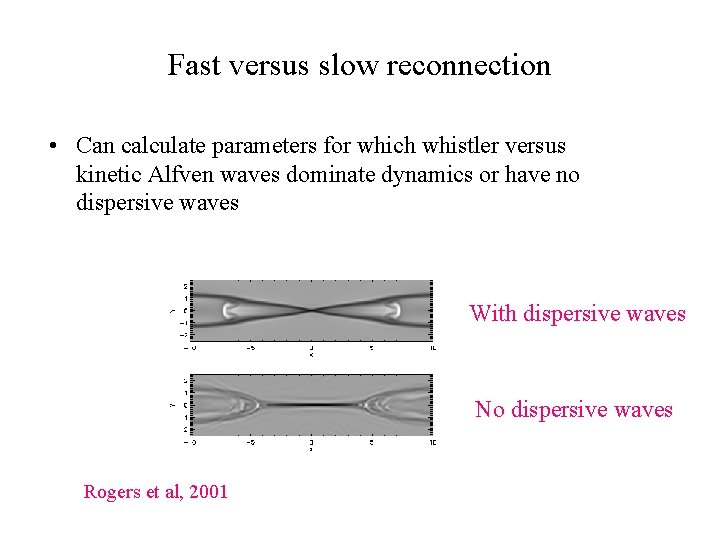
Fast versus slow reconnection • Can calculate parameters for which whistler versus kinetic Alfven waves dominate dynamics or have no dispersive waves With dispersive waves No dispersive waves Rogers et al, 2001

Wave dispersion and the structure of nozzle • Controlled by the variation of the wave phase speed with distance from the x-line – increasing phase speed • Closing of nozzle • MHD case since Bn and CA increase with distance from the x-line - decreasing phase speed • Opening of the nozzle • Whistler or kinetic Alfven waves v ~ B/w

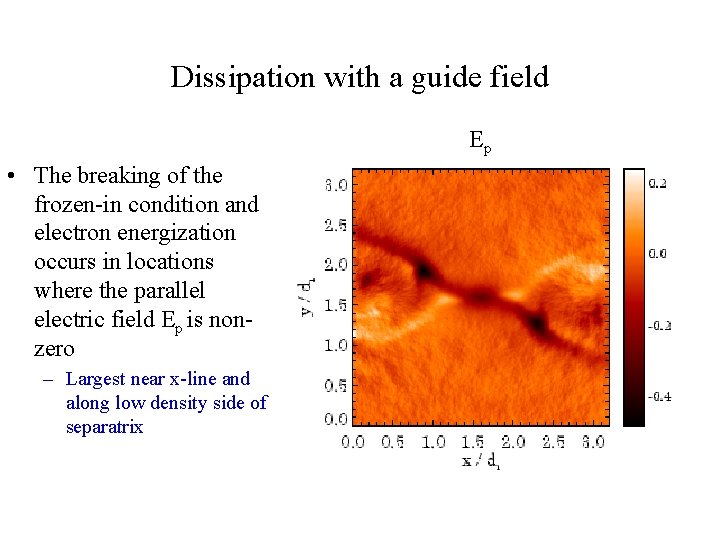
Dissipation with a guide field Ep • The breaking of the frozen-in condition and electron energization occurs in locations where the parallel electric field Ep is nonzero – Largest near x-line and along low density side of separatrix

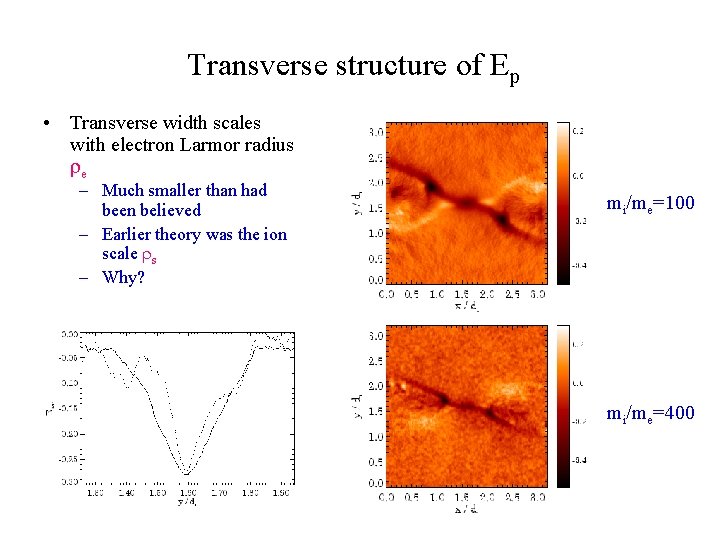
Transverse structure of Ep • Transverse width scales with electron Larmor radius e – Much smaller than had been believed – Earlier theory was the ion scale s – Why? mi/me=100 mi/me=400

Structure of Ep • The structure of Ep is controlled by the development of an electrostatic field that shorts out the parallel inductive electric field • Earlier theories predicted the transverse scale s – incorrect because presumed ions magnetized – For small transverse scales ions are unmagnetized – Transverse scale is es

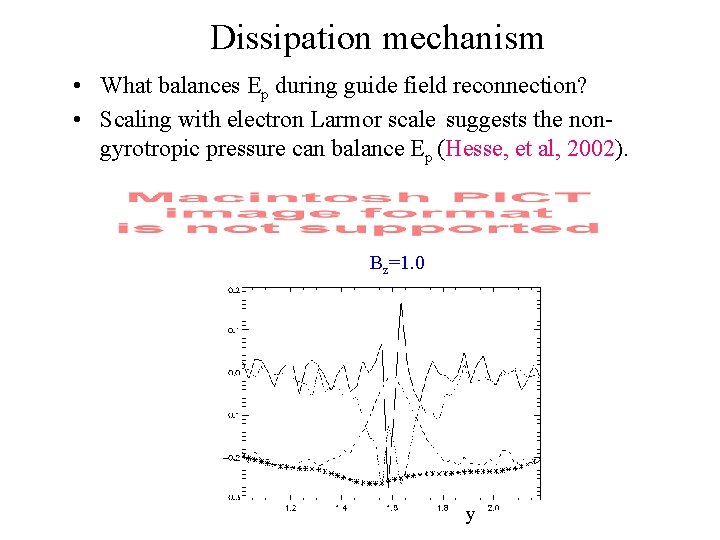
Dissipation mechanism • What balances Ep during guide field reconnection? • Scaling with electron Larmor scale suggests the nongyrotropic pressure can balance Ep (Hesse, et al, 2002). Bz=1. 0 y

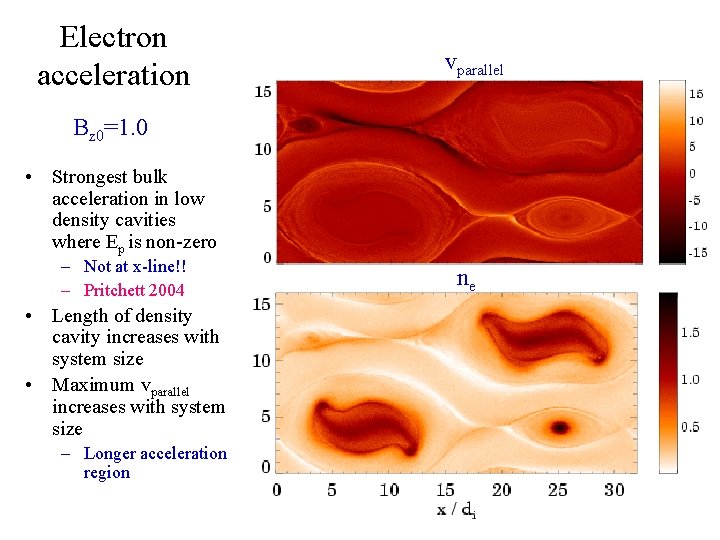
Electron acceleration vparallel Bz 0=1. 0 • Strongest bulk acceleration in low density cavities where Ep is non-zero – Not at x-line!! – Pritchett 2004 • Length of density cavity increases with system size • Maximum vparallel increases with system size – Longer acceleration region ne

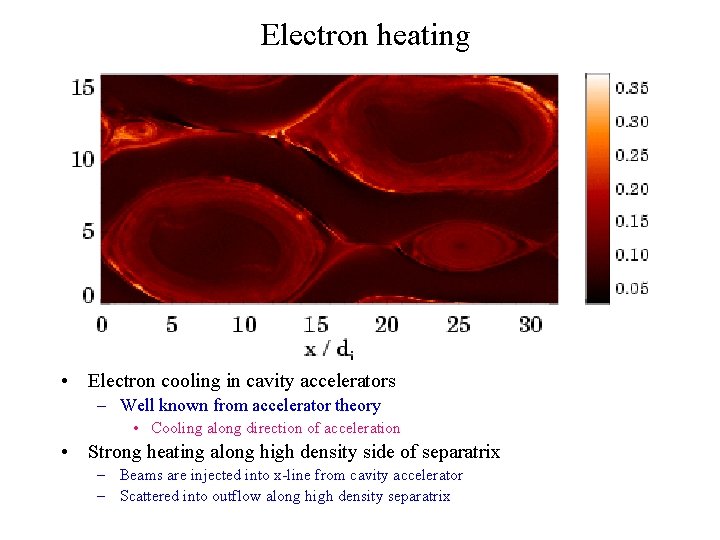
Electron heating • Electron cooling in cavity accelerators – Well known from accelerator theory • Cooling along direction of acceleration • Strong heating along high density side of separatrix – Beams are injected into x-line from cavity accelerator – Scattered into outflow along high density separatrix

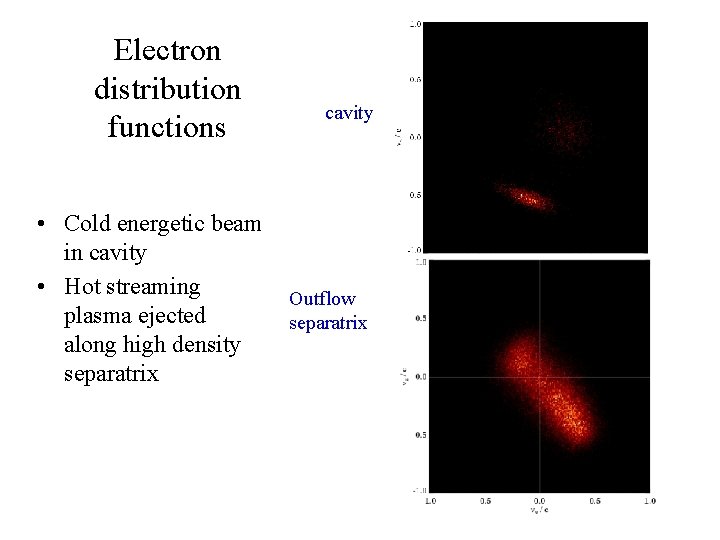
Electron distribution functions • Cold energetic beam in cavity • Hot streaming plasma ejected along high density separatrix cavity Outflow separatrix

Structuring of the Parallel Electric Field during 3 -D Magnetic Reconnection with guide field • Bz=5. 0 Bx, mi/me=100 • Development of strong current layer – Buneman instability evolves into electron holes y x

Formation of Electron holes • Intense electron beam generates Buneman instability – nonlinear evolution into “electron holes” • localized regions of intense positive potential and associated bipolar parallel electric field Ez z B x

Anomalous drag on electrons • Parallel electric field scatter electrons producing effective drag • Average over fluctuations along z direction to produce a mean field electron momentum equation – correlation between density and electric field fluctuations yields drag • Normalized electron drag

Electron drag due to scattering by parallel electric fields • Drag Dz has complex spatial y and temporal structure with positive and negative values • Results not consistent with the quasilinear model • How far along separatrix does turbulence spread? x

Structuring of the parallel electric field along separatrix: 2 -D • Strong electron beams break up Ep into localized structures – Electron holes and double layers – Most intense in density cavities – In 2 -D not near x-line because beams in out-of-plane direction

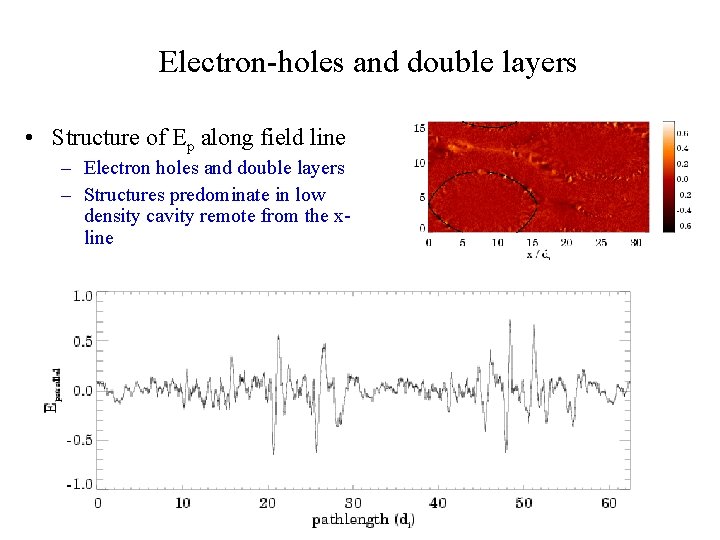
Electron-holes and double layers • Structure of Ep along field line – Electron holes and double layers – Structures predominate in low density cavity remote from the xline

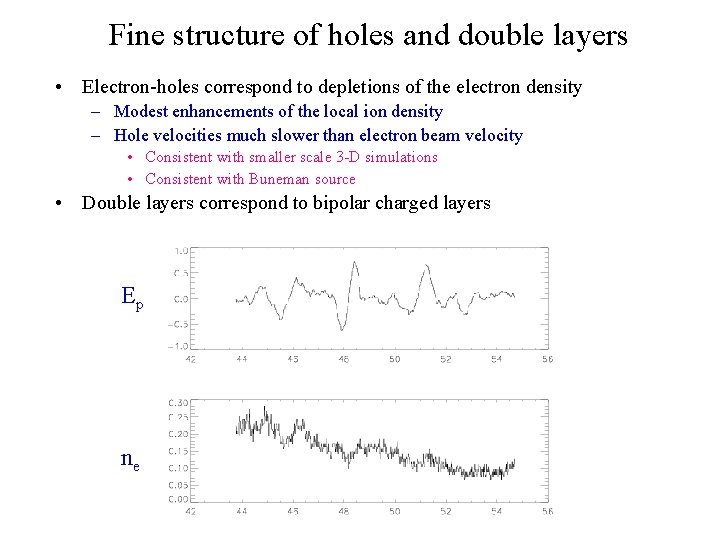
Fine structure of holes and double layers • Electron-holes correspond to depletions of the electron density – Modest enhancements of the local ion density – Hole velocities much slower than electron beam velocity • Consistent with smaller scale 3 -D simulations • Consistent with Buneman source • Double layers correspond to bipolar charged layers Ep ne

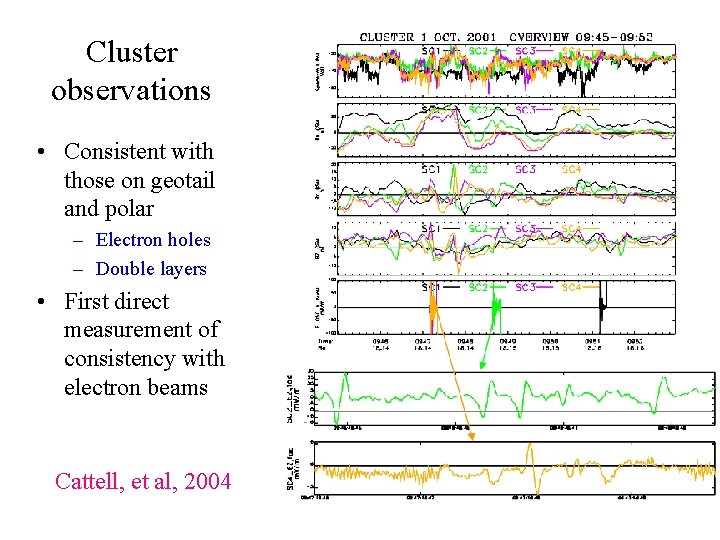
Cluster observations • Consistent with those on geotail and polar – Electron holes – Double layers • First direct measurement of consistency with electron beams Cattell, et al, 2004

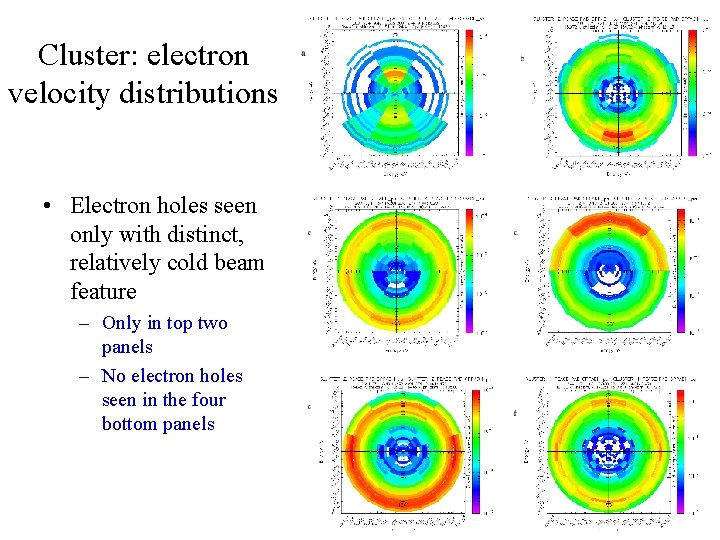
Cluster: electron velocity distributions • Electron holes seen only with distinct, relatively cold beam feature – Only in top two panels – No electron holes seen in the four bottom panels

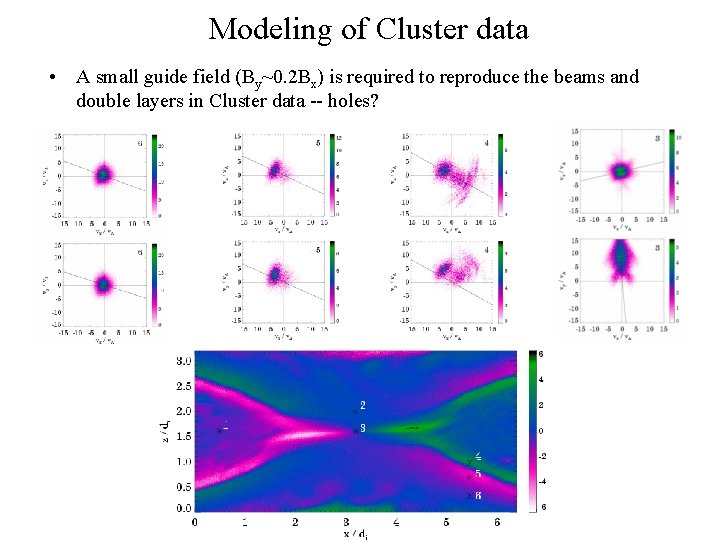
Modeling of Cluster data • A small guide field (By~0. 2 Bx) is required to reproduce the beams and double layers in Cluster data -- holes?

Structure of parallel electric fields in Nature • Electron holes and double layers have long been observed in the auroral region of the ionosphere – Temerin, et al. 1982, Mozer, et al. 1997 – Auroral dynamics are not linked to magnetic reconnection • Observations and theory now suggest that such structures form in essentially all of the boundary layers present in the Earth’s magnetosphere where reconnection takes place – Magnetotail, magnetopause • More generally, evidence is now strong that uniform, largescale parallel electric fields do not exist in Nature – Dissipation always take place in localized non-linear structures – Consequences for understanding particle heating?

Conclusions • Fast reconnection requires either the coupling to dispersive waves at small scales or a mechanism for anomalous resistivity • The kinetic Alfven wave dominates in cases with a large guide field • The transverse scale length of the region where the parallel electric field is non-zero is much smaller than thought previously – Scales with an effective electron Larmor radius

Conclusions (cont. ) • Non-gyrotropic pressure continues to balance the parallel electric field near the x-line (Hesse, et al, 2002) – Consequence of the small spatial scales • Electron acceleration and heating is controlled by a spatially non-local region of depleted electron density (Tanaka, 1997; Pritchett and Coroniti, 2004) – Low density cavity is a region of extended non-zero parallel electric field – An efficient plasma accelerator – Electron heating results from the injection of energetic electrons from this cavity into the x-line

Conclusions (cont. ) • Strong electron beams in the low density cavity produce electron-holes and double layers even in a 2 -D simulation • Electron beams are seen in the magnetotail by Cluster when and only when electron holes and double layers are observed (Cattell, et al, 2004). – Consistent with theory – Consistent with earlier auroral observations – Large-scale parallel electric fields are unlikely to exist in Nature.