The Structure of Scientific Collaboration Networks by M

The Structure of Scientific Collaboration Networks by M. E. J. Newman CMSC 601 Paper Summary Marie des. Jardins January 27, 2009

Outline n n n Overview Social networks Scientific collaboration networks q q n n Properties Data sets Results Conclusions

Overview n n n Computationally analyze scientific collaboration networks Uses actual data sets from online archives Findings: q q small-world property presence of “clustering” power law distribution of #collaborators, #papers different patterns in different fields

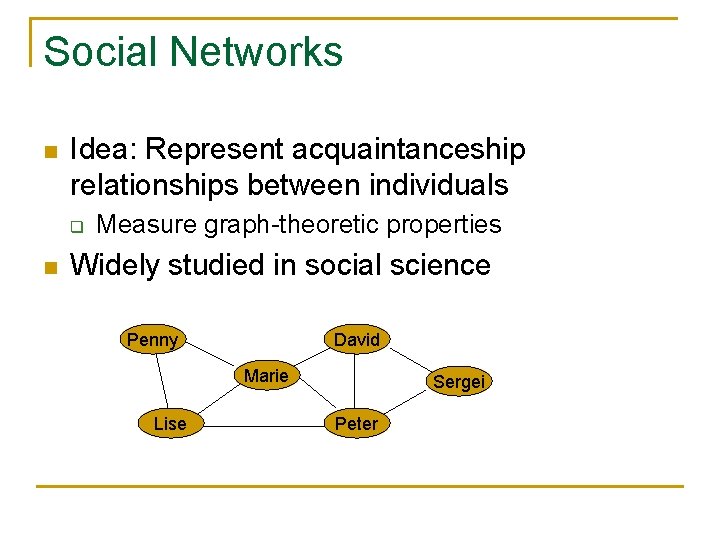
Social Networks n Idea: Represent acquaintanceship relationships between individuals q n Measure graph-theoretic properties Widely studied in social science Penny David Marie Lise Sergei Peter

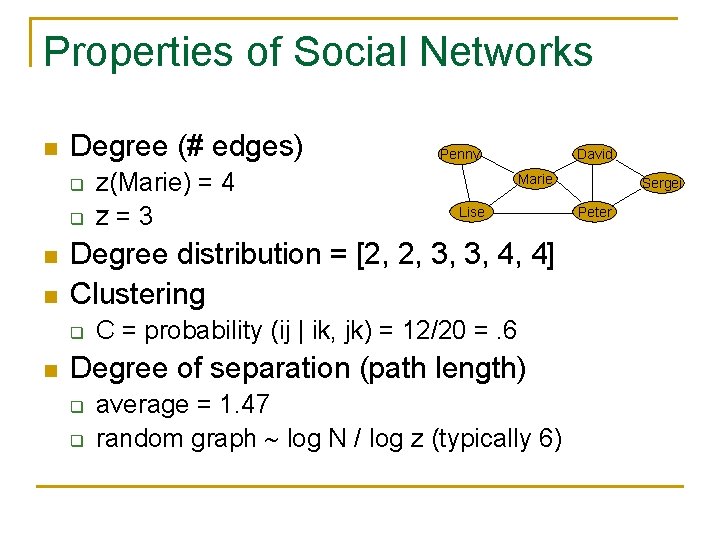
Properties of Social Networks n Degree (# edges) q q n n David Marie Lise Degree distribution = [2, 2, 3, 3, 4, 4] Clustering q n z(Marie) = 4 z=3 Penny C = probability (ij | ik, jk) = 12/20 =. 6 Degree of separation (path length) q q average = 1. 47 random graph log N / log z (typically 6) Sergei Peter

Scientific Collaboration Networks n n Represent co-authorship relationships Data sets: q q n Biomedical research (MEDLINE) Theoretical physics (Los Alamos e-Print Archive (arxiv)) High-energy physics (SPIRES) Computer science (NCSTRL) Papers from 1995 -1999 q 13 K – 2 M papers

Erdös Number n Paul Erdös q q Famous Hungarian mathematician Published over 1400 papers! Erdös Number = co-authorship distance to Erdös Marie’s Erdös Number = ? ?

Counting Authors n Ambiguity in names (first name vs. first initial vs. all initials) q q Two counts: all initials vs. 1 st initial Upper/lower bounds on number of authors

General Properties n n Average number of papers per author: 4 Average number of authors per paper: 3 q n Average number of collaborators: q n Ranges from 4 (high-energy theory) to 173 (SPIRES) Size of largest connected component: q n Max: 1681!! (SPIRES) Ranges from 60% (CS) to 90% (astrophysics) Amount of clustering: q Ranges from 7% (MEDLINE) to 73% (SPIRES)

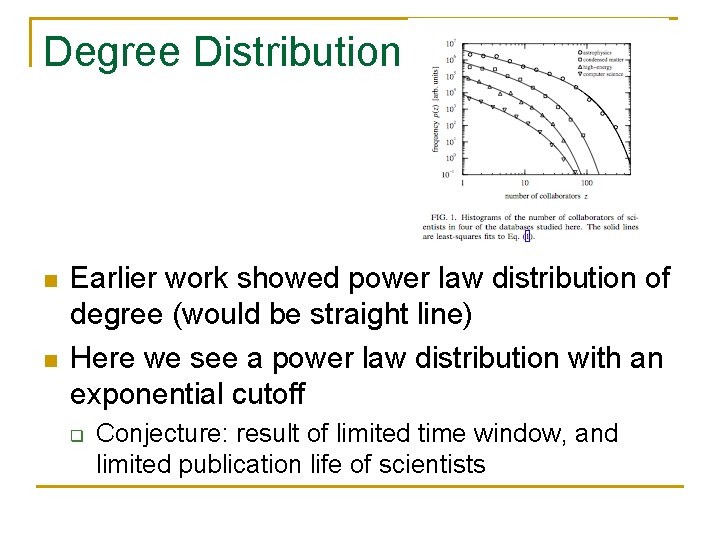
Degree Distribution n n Earlier work showed power law distribution of degree (would be straight line) Here we see a power law distribution with an exponential cutoff q Conjecture: result of limited time window, and limited publication life of scientists

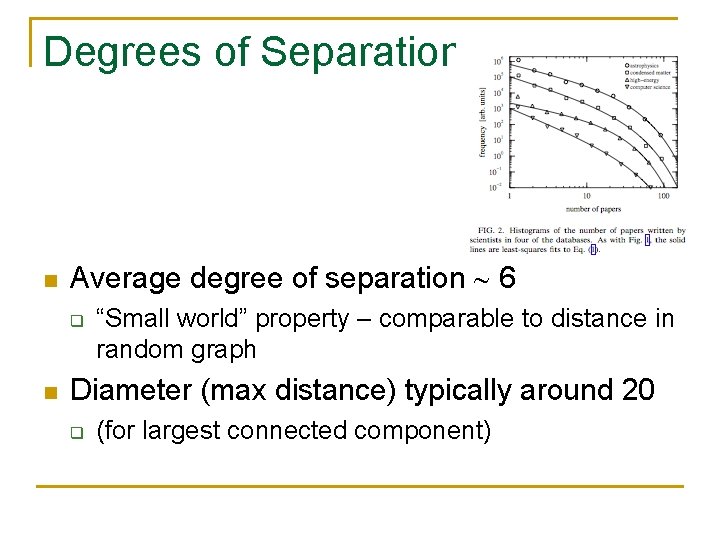
Degrees of Separation n Average degree of separation 6 q n “Small world” property – comparable to distance in random graph Diameter (max distance) typically around 20 q (for largest connected component)

Summary n Scientific collaboration networks q q n Social networks exhibiting interesting structure Lots of available data Key characteristics q q High clustering Small-world property Power-law distribution of #authors, #papers Properties vary across fields