The Structure of Constraint Satisfaction Problems Elitza Maneva

The Structure of Constraint Satisfaction Problems Elitza Maneva, IBM Joint work with: Parikshit Gopalan, U Washington Phokion Kolaitis, IBM Christos Papadimitriou, UC Berkeley

Statistical mechanics and CSPs • Why do we need to look at general CSPs? • How does local combinatorial structure determine global properties of a system? • Note: This talk is not about random problems, but about guaranteed combinatorial properties.
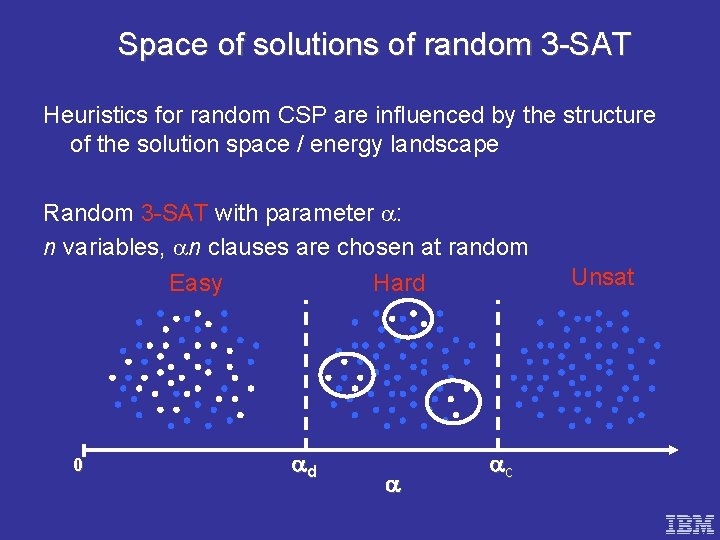
Space of solutions of random 3 -SAT Heuristics for random CSP are influenced by the structure of the solution space / energy landscape Random 3 -SAT with parameter : n variables, n clauses are chosen at random Easy Hard 0 d c Unsat
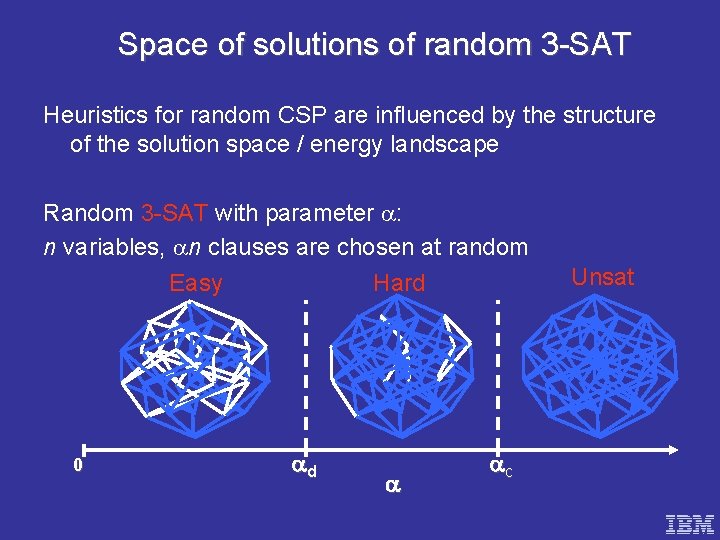
Space of solutions of random 3 -SAT Heuristics for random CSP are influenced by the structure of the solution space / energy landscape Random 3 -SAT with parameter : n variables, n clauses are chosen at random Easy Hard 0 d c Unsat

Clustering in random CSP What is known? 2 -SAT: a single cluster up to the satisfiability threshold 3 -SAT to 7 -SAT: not known, but conjectured to have clusters before the satisfiability threshold 8 -SAT and above: exponential number of clusters [Mezard, Mora, Zecchina `05] [Achlioptas, Ricci-Tersenghi `06]

Plan • Constraint satisfaction problems: – – 3 -SAT 3 -colorability Equations mod 2 (XOR-SAT) General CSP • Computational complexity of CSPs – Boolean variables [Schaefer `78] – Progress on non-Boolean CSP [Bulatov `02], [Hell-Nesetril `90] • The space of solutions of CSPs – Boolean variables: [Gopalan, Kolaitis, Maneva, Papadimitriou `06] – Directions
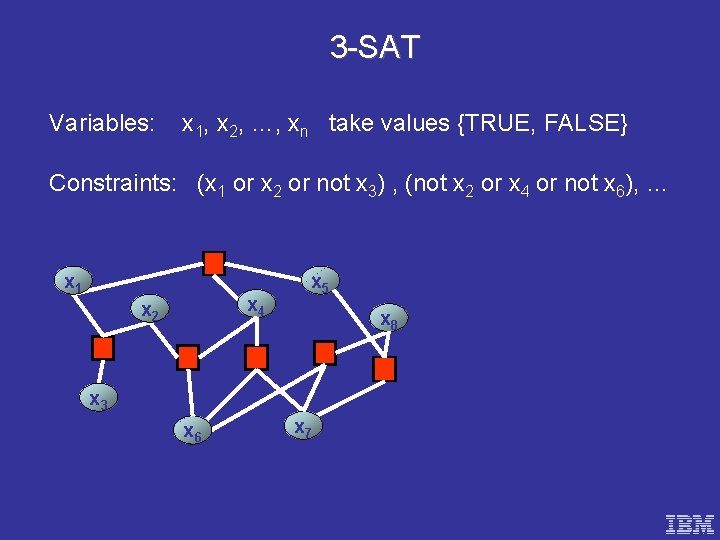
3 -SAT Variables: x 1, x 2, …, xn take values {TRUE, FALSE} Constraints: (x 1 or x 2 or not x 3) , (not x 2 or x 4 or not x 6), … x 1 x 4 x 2 x 5 x 8 x 3 x 6 x 7
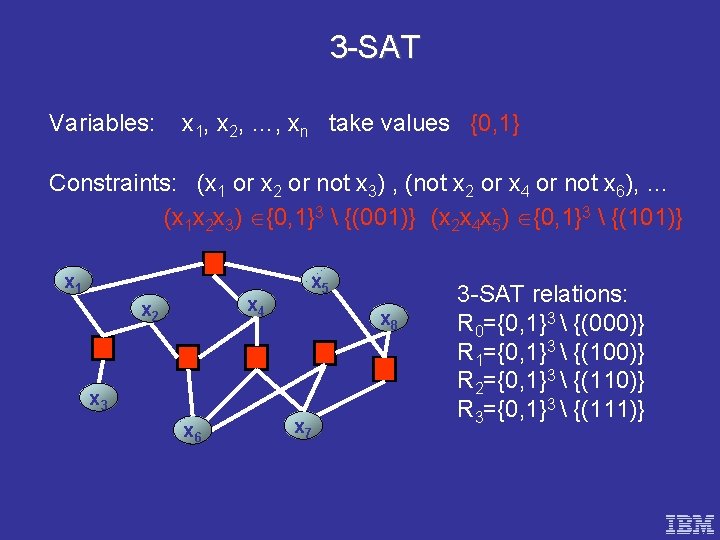
3 -SAT Variables: x 1, x 2, …, xn take values {0, 1} Constraints: (x 1 or x 2 or not x 3) , (not x 2 or x 4 or not x 6), … (x 1 x 2 x 3) {0, 1}3 {(001)} (x 2 x 4 x 5) {0, 1}3 {(101)} x 1 x 4 x 2 x 5 x 8 x 3 x 6 x 7 3 -SAT relations: R 0={0, 1}3 {(000)} R 1={0, 1}3 {(100)} R 2={0, 1}3 {(110)} R 3={0, 1}3 {(111)}
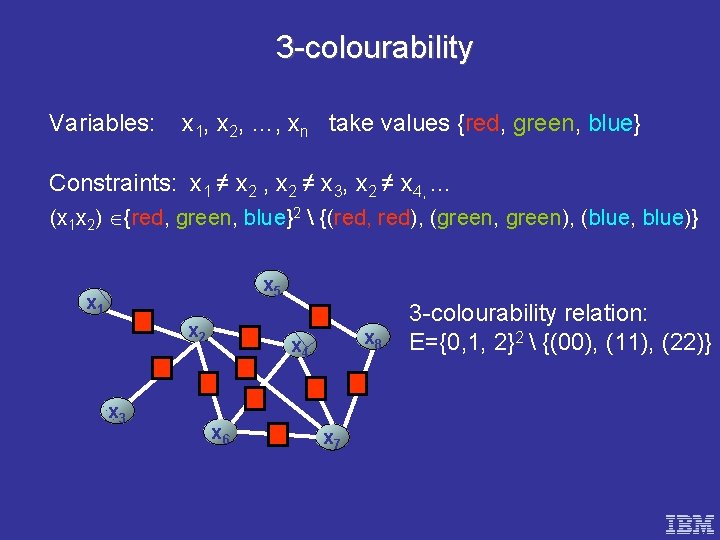
3 -colourability Variables: x 1, x 2, …, xn take values {red, green, blue} Constraints: x 1 ≠ x 2 , x 2 ≠ x 3, x 2 ≠ x 4, . . . (x 1 x 2) {red, green, blue}2 {(red, red), (green, green), (blue, blue)} x 5 x 1 x 2 x 3 x 8 x 4 x 6 x 7 3 -colourability relation: E={0, 1, 2}2 {(00), (11), (22)}
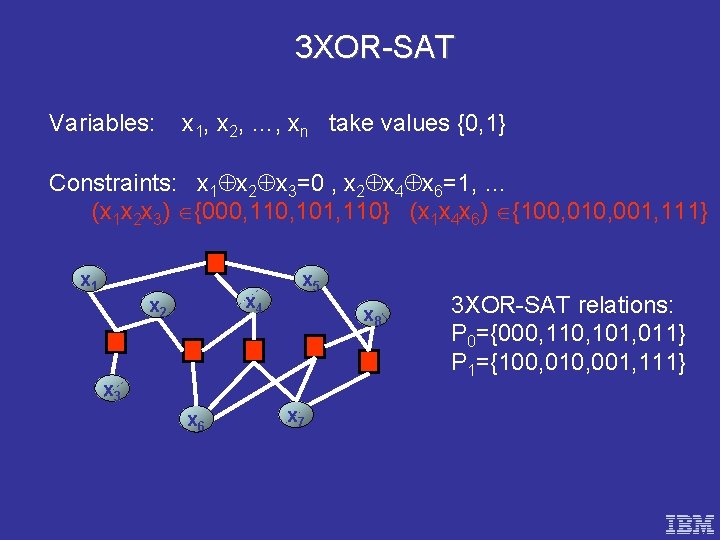
3 XOR-SAT Variables: x 1, x 2, …, xn take values {0, 1} Constraints: x 1 x 2 x 3=0 , x 2 x 4 x 6=1, … (x 1 x 2 x 3) {000, 110, 101, 110} (x 1 x 4 x 6) {100, 010, 001, 111} x 1 x 4 x 2 x 5 x 8 x 3 x 6 x 7 3 XOR-SAT relations: P 0={000, 110, 101, 011} P 1={100, 010, 001, 111}
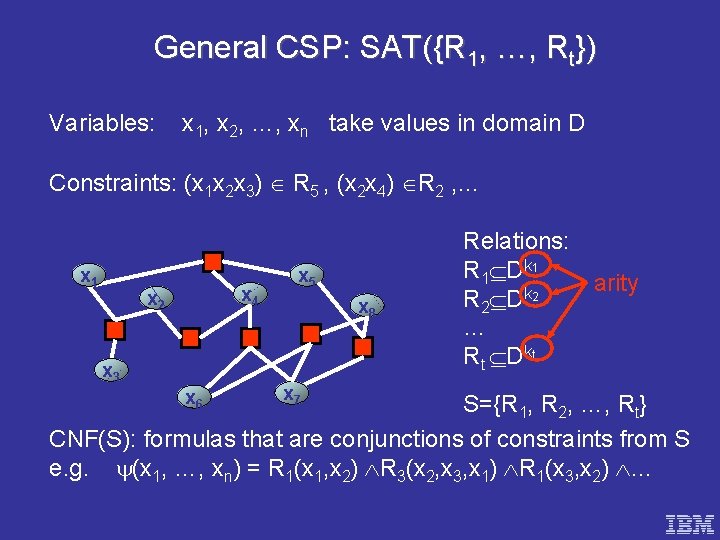
General CSP: SAT({R 1, …, Rt}) Variables: x 1, x 2, …, xn take values in domain D Constraints: (x 1 x 2 x 3) R 5 , (x 2 x 4) R 2 , … x 1 x 4 x 2 x 3 x 6 x 5 x 8 x 7 Relations: R 1 Dk 1 arity k 2 R 2 D … Rt Dkt S={R 1, R 2, …, Rt} CNF(S): formulas that are conjunctions of constraints from S e. g. (x 1, …, xn) = R 1(x 1, x 2) R 3(x 2, x 3, x 1) R 1(x 3, x 2) …

Some easy CSPs • 2 -SAT : – D={0, 1} , S = {relations of arity 2} • Horn-SAT : – D={0, 1}, S = {clauses with at most one positive literal} = = { {0}, {1}, {00, 11}, {01, 10, 00}, {0, 1}3{(110)}, {0, 1}3{(111)} } • dual. Horn-SAT : – D={0, 1}, S = {clauses with at most one negative literal} = = { {0}, {1}, {00, 11}, {01, 10, 11}, {0, 1}3{(100)}, {0, 1}3{(000)} } • SEPOD-3 SAT (Some Easy Problem Of Domain-size 3): – D={0, 1, 3}, S={R}={ { (01), (10), (12), (21) } }
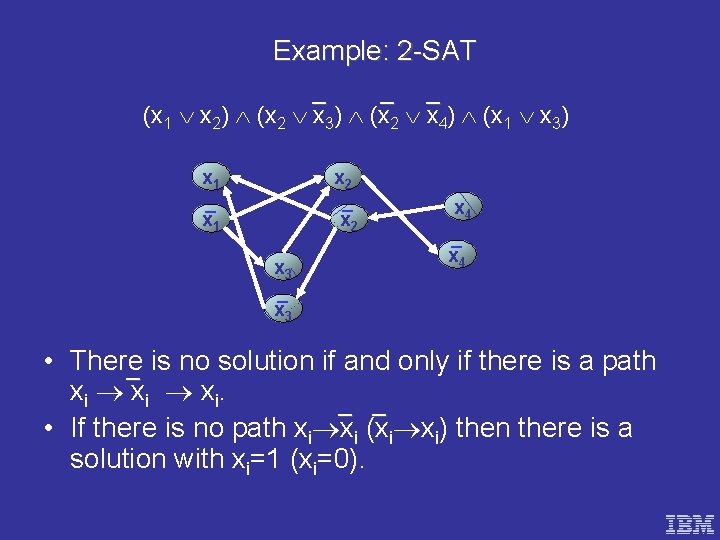
Example: 2 -SAT _ _ _ (x 1 x 2) (x 2 x 3) (x 2 x 4) (x 1 x 3) x 1 _ x 1 x 2 _ x 2 x 3 _ x 3 x 4 _ x 4 • There _ is no solution if and only if there is a path xi xi. _ _ • If there is no path xi xi (xi xi) then there is a solution with xi=1 (xi=0).

Example: Horn-SAT _ _ _ _ (x 1 x 2) (x 3) (x 1 x 2 x 4) (x 3 x 4) (x 2 x 5) (x 1 x 2 x 3) 1 0 • Propagate unit clauses • After no unit clauses are left, assign remaining variables to 0

Plan • Constraint satisfaction problems: – – 3 -SAT 3 -colorability Equations mod 2 (XOR-SAT) General CSP • Computational complexity of CSPs – Boolean variables [Schaefer `78] – Progress on non-Boolean CSP [Bulatov `02], [Hell-Nesetril `90] • The space of solutions of CSPs – Boolean variables: [Gopalan, Kolaitis, Maneva, Papadimitriou `06] – Directions

Complexity of Boolean Satisfiability Given just S={R 1, …, Rt}, can we say if the problem SAT(S) is in P, or NP-complete or neither? Theorem [Schaefer `78] For |D|=2: • SAT(S) is polynomial time if S is s. t. : 1. Every Ri can be written as a 2 -SAT formula. 2. Every Ri can be written as a XOR-SAT formula 3. Every Ri can be written as a Horn-SAT formula 4. Every Ri can be written as a dual. Horn-SAT formula • In all other cases SAT(S) is NP-complete.

How do we recognize that SAT(S) is in P? Can R be written as a 2 -SAT formula? e. g. R(x 1, x 2, x 3) = {011, 101, 001, 100} _ _ = (x 1 x 2) (x 1 x 3) Theorem: A k-ary relation R is expressible as a 2 -SAT formula if and only if it holds that: if (a 1 a 2…ak) R (b 1 b 2…bk) R (c 1 c 2…ck) R , then (maj(a 1 b 1 c 1) maj(a 2 b 2 c 2)…maj(akbkck)) R.

Closure properties of easy Boolean CSPs • For a logical relation R it holds that – R is expressible as a 2 SAT formula if and only if R is closed under maj(a, b, c) – R is expressible as a XOR-SAT formula iff is closed under a b c R – R is expressible as a Horn-SAT formula iff is closed under a b R – R is exprssible as a dual. Horn-SAT formula iff R is closed under a b

3 -SAT and reductions • What about relations expressible as 3 -SAT? • n 2 2 possible solutions sets, 28 (n 3 ) possible 3 -SAT formulas • Schaefer’s Expressibility Theorem If S is such that there are relation in S that are not expressible as 2 -SAT, XOR-SAT Horn, and dual-Horn, then for any relation R {0, 1}k there exists a formula (x 1, …, xk, w 1, …, wr) CNF(S) such that R(x 1, …, xk) = w 1 w 2…wr (x 1, x 2, …, xk, w 1, w 2, …, wr)
Schaefer expressibility A relation R is expressible from set of relations S if there is a CNF(S) formula , s. t. : R (x 1, …, xk) = w 1, … , wt (x 1, …, xk, w 1, …, wt)

3 -SAT and reductions • What about relations expressible as 3 -SAT? • n 2 2 possible solutions sets, 28 (n 3 ) possible 3 -SAT formulas • Schaefer’s Expressibility Theorem If S is such that there are relation in S that are not expressible as 2 -SAT, XOR-SAT Horn, and dual-Horn, then for any relation R {0, 1}k there exists a formula (x 1, …, xk, w 1, …, wr) CNF(S) such that R(x 1, …, xk) = w 1 w 2…wr (x 1, x 2, …, xk, w 1, w 2, …, wr) • Corollary: Under the above conditions for S, SAT(S) is at least as hard as 3 -SAT.
![What about other CSPs? • [Bulatov `02] If |D|=3 SAT(S) is either in P What about other CSPs? • [Bulatov `02] If |D|=3 SAT(S) is either in P](http://slidetodoc.com/presentation_image/29c18df399432458e582444f387c7313/image-22.jpg)
What about other CSPs? • [Bulatov `02] If |D|=3 SAT(S) is either in P or NPcomplete (and characterized by closure properties). • [Hell-Nesetril `90] If R is a binary relation SAT({R}) is in P if R is a bipartite graph, NP-compete otherwise. • |D| ≥ 4: open What closure properties guarantee the existence of a polynomial time algorithm?

Plan • Constraint satisfaction problems: – – 3 -SAT 3 -colorability Equations mod 2 (XOR-SAT) General CSP • Computational complexity of CSPs – Boolean variables [Schaefer `78] – Progress on non-Boolean CSP [Bulatov `02], [Hell-Nesetril `90] • The space of solutions of CSPs – Boolean variables: [Gopalan, Kolaitis, Maneva, Papadimitriou `06] – Directions

Space of solutions 11111 00000 n-dimensional hypercube

Space of solutions 11111 00000
Space of solutions 11111 00000
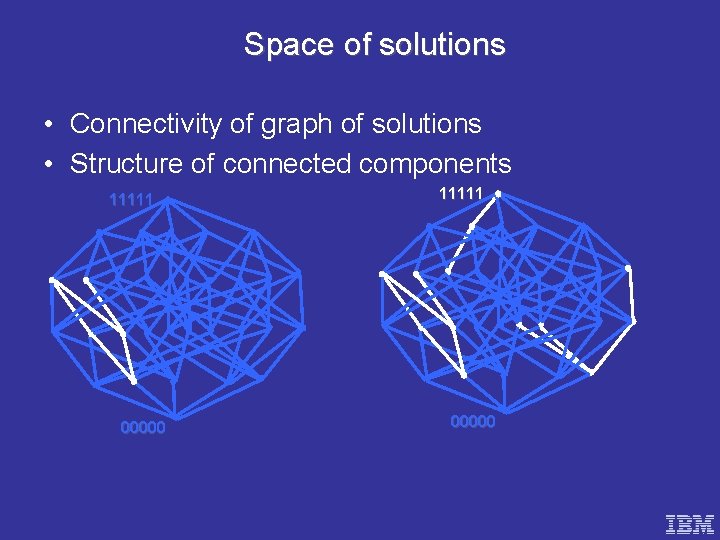
Space of solutions • Connectivity of graph of solutions • Structure of connected components 11111 00000

Our dichotomy • Computational problems – st-CONN: Are two given solutions connected? – CONN: Is the solution graph connected? • Structural property – Possible diameter of components Tight CSP Non-tight CSP st-CONN in P PSPACE-complete CONN in co-NP PSPACE-complete diameter linear exponential SAT P and NP-complete

Our dichotomy Tight CSP Non-tight CSP st-CONN in P PSPACE-complete CONN in co-NP PSPACE-complete diameter linear exponential specific graphs “any” graph expressiveness

Tight Problems S={R 1, . . , Rt}. CSP(S) is • OR-free if for every Ri Ri cannot express OR by substituting constants • NAND-free if for every Ri Ri cannot express NAND by substituting constants • Component-wise 2 -SAT if for every Ri every connected component of Ri is a 2 -SAT formula
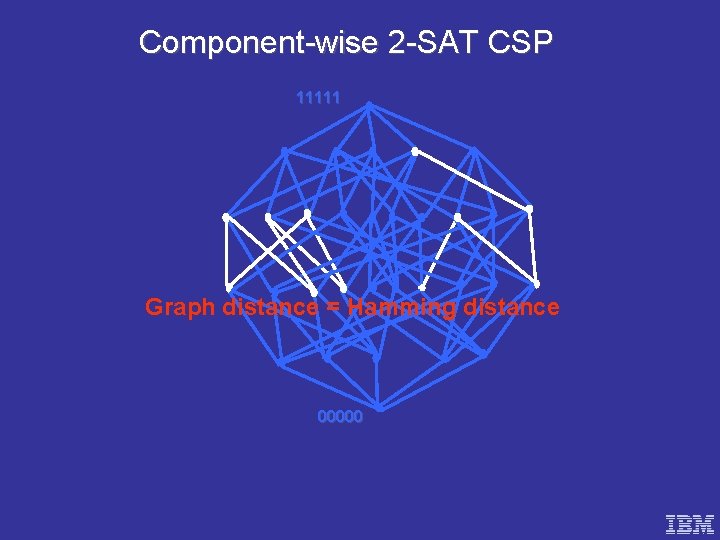
Component-wise 2 -SAT CSP 11111 Graph distance = Hamming distance 00000
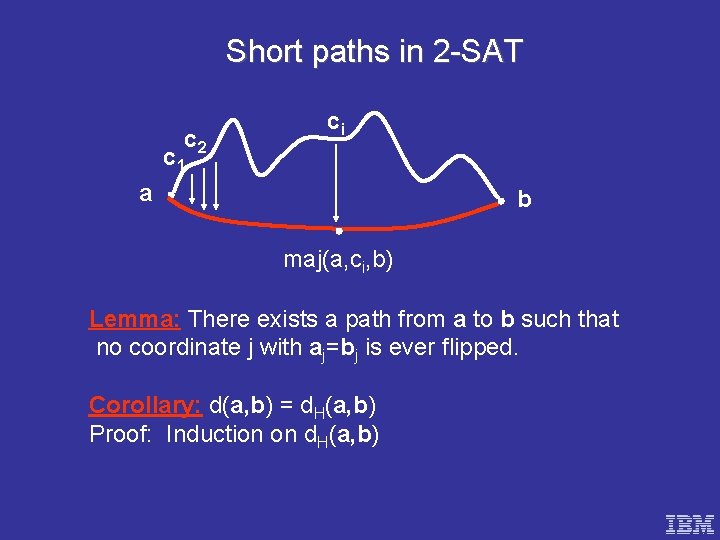
Short paths in 2 -SAT c 2 ci c 1 a b maj(a, ci, b) Lemma: There exists a path from a to b such that no coordinate j with aj=bj is ever flipped. Corollary: d(a, b) = d. H(a, b) Proof: Induction on d. H(a, b)
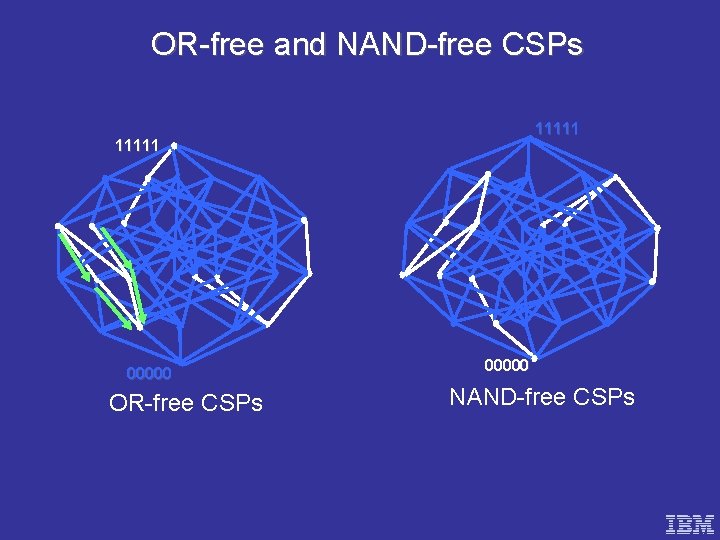
OR-free and NAND-free CSPs 11111 00000 OR-free CSPs 00000 NAND-free CSPs

Our dichotomy Tight CSP CONN in co. NP st-CONN in P diameter linear expressiveness specific graphs Non-tight CSP

Large diameter 3 -SAT formula 11 10 01 • 1(x 1, x 2)=(x 1 x 2) 00 • 2(x 1, x 2, x 3, x 4)= (x 3 x 4) 1(x 1, x 2) x 3 x 4=(11) x 3 x 4=(10) x 3 x 4=(01) x 3 x 4=(00)

Large diameter 3 -SAT formula 11 10 01 • 1(x 1, x 2)=(x 1 x 2) 00 • 2(x 1, x 2, x 3, x 4)= (x 3 x 4) 1(x 1, x 2) x 3 x 4=(11) x 3 x 4=(10) x 3 x 4=(01) x 3 x 4=(00)

Large diameter 3 -SAT formula 11 10 01 • 1(x 1, x 2)=(x 1 x 2) 00 _ _ • 2(x 1, x 2, x 3, x 4)= (x 3 x 4) 1(x 1, x 2) . (x 3 x 4 x 1) (x 3 x 4 x 2) x 3 x 4=(11) x 3 x 4=(10) x 3 x 4=(01) x 3 x 4=(00)

Large diameter 3 -SAT formula 11 10 01 • 1(x 1, x 2)=(x 1 x 2) 00 _ _ • 2(x 1, x 2, x 3, x 4)= (x 3 x 4) 1(x 1, x 2) . (x 3 x 4 x 1) (x 3 x 4 x 2) x 3 x 4=(11) x 3 x 4=(01) x 3 x 4=(10) x 3 x 4=(00) • k(x 1, …, x 2 k) is a path from s to t of length ≥ 2 k • k+1(x 1, …, x 2 k+2) = (x 2 k-1 x 2 k) k(x 1, …, x 2 k) X 2 k-1 x 2 k=(11) X 2 k-1 x 2 k=(10) X 2 k-1 x 2 k=(01)

Large diameter 3 -SAT formula 11 10 01 • 1(x 1, x 2)=(x 1 x 2) 00 _ _ • 2(x 1, x 2, x 3, x 4)= (x 3 x 4) 1(x 1, x 2) . (x 3 x 4 x 1) (x 3 x 4 x 2) x 3 x 4=(11) x 3 x 4=(01) x 3 x 4=(10) x 3 x 4=(00) • k(x 1, …, x 2 k) is a path from s to t of length ≥ 2 k k • k+1(x 1, …, x 2 k+2) = (x 2 k-1 x 2 k) k(x 1, …, x 2 k) _ _. (x 2 k-1 x 2 k (xi=si)) i=1 path of length ≥ 2 X 2 k-1 x 2 k=(11) 2 k X 2 k-1 x 2 k=(10) X 2 k-1 x 2 k=(01)
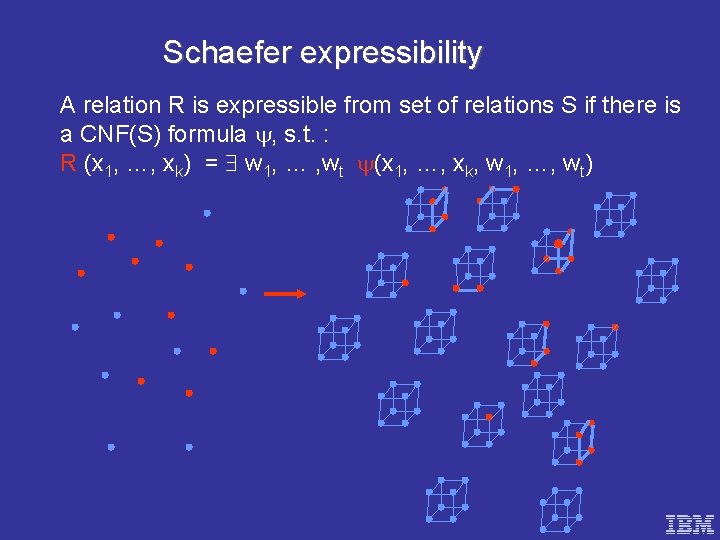
Schaefer expressibility A relation R is expressible from set of relations S if there is a CNF(S) formula , s. t. : R (x 1, …, xk) = w 1, … , wt (x 1, …, xk, w 1, …, wt)

Faithful expressibility A relation is faithfully expressible from set of relations S if there is a CNF(S) formula , s. t. : (x 1, …, xn) = w 1, … , wt (x 1, …, xn, w 1, …, wt)

Faithful expressibility A relation is faithfully expressible from set of relations S if there is a CNF(S) formula , s. t. : (x 1, …, xn) = w 1, … , wt (x 1, …, xn, w 1, …, wt)

Proof for the hard side of the dichotomy Lemma: For 3 -SAT (a) Exist formulas with exponential diameter (b) CONN and st-CONN are PSPACE-complete Lemma: Faithful expressibility: (a) preserves diameter up to a polynomial factor (b) Is a poly time reduction for CONN and st-CONN Faithful Expressibility Theorem: If S is not tight, every relation is faithfully expressible from S.

Faithful expressibility A relation is faithfully expressible from set of relations S if there is a CNF(S) formula , s. t. : (x 1, …, xn) = w 1, … , wt (x 1, …, xn, w 1, …, wt) and (1) For every a {0, 1}n with (a)=1, the graph of solutions of (a, w) is connected. (2) For every a, b {0, 1}n with (a)= (b)=1, |a-b|=1, there exists w s. t. (a, w)= (b, w)=1

Faithful Expressibility Theorem : If S is not tight, every relation is faithfully expressible from S. Proof in 4 steps. Step 0: Express 2 -SAT clauses. • Some relation can express OR (NAND). • Other 2 -SAT clauses by resolution: _ _ _ (x 1 x 2) = w (x 1 w) (w x 2)

Faithful Expressibility Theorem : If S is not tight, every relation is faithfully expressible from S. Proof in 4 steps. Step 1 : Express a relation where some distance expands. Use R which is not component-wise bijunctive. (x 1 x 3) =
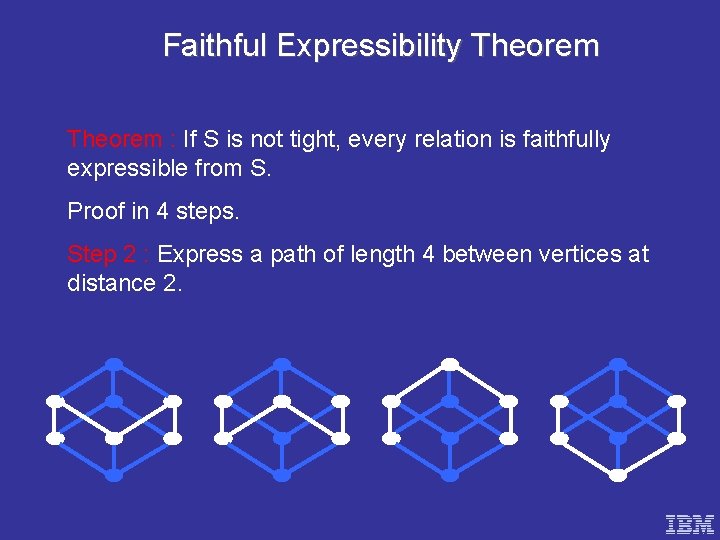
Faithful Expressibility Theorem : If S is not tight, every relation is faithfully expressible from S. Proof in 4 steps. Step 2 : Express a path of length 4 between vertices at distance 2.

Faithful Expressibility Theorem : If S is not tight, every relation is faithfully expressible from S. Proof in 4 steps. Step 3: Express all 3 -SAT clauses from such paths. [Hearne-Demaine ‘ 02]

Faithful Expressibility Theorem : If S is not tight, every relation is faithfully expressible from S. Proof in 4 steps. Step 4: Express all relations from 3 -SAT clauses.

Directions • Can we extend this result to larger domains? (Also determine the complexity of the satisfiability problem for larger domains. ) • Study the structure of the space of assignments (energy landscape) i. e. not just solutions, but near solutions. • Weaken the notion of connectivity. • What are the properties of the solution space of random instances of different Boolean CSP? Which Boolean CSPs have a clustered phase?

Thank you
![Other dichotomy results on Boolean CSP Counting solutions [Creignou-Hermann `96] Inverse satisfiability [Kavvadias-Sideri `98] Other dichotomy results on Boolean CSP Counting solutions [Creignou-Hermann `96] Inverse satisfiability [Kavvadias-Sideri `98]](http://slidetodoc.com/presentation_image/29c18df399432458e582444f387c7313/image-52.jpg)
Other dichotomy results on Boolean CSP Counting solutions [Creignou-Hermann `96] Inverse satisfiability [Kavvadias-Sideri `98] Unique satisfiability [Juban `99] Approximability [Creignou `95] [Khanna-Sudan-Trevisan-Williamson `01], Minimal satisfiability [Kirousis-Kolaitis `03] Propositional abduction [Creignou-Zanuttini `06]
- Slides: 52