The strange world of Quantum Mechanics It is

The strange world of Quantum Mechanics “It is impossible for both The Ultimate Answer and the Ultimate Question to be known about in the same universe, as they will cancel each other out and take the Universe with them, to be replaced by something even more bizarre. . ” 1

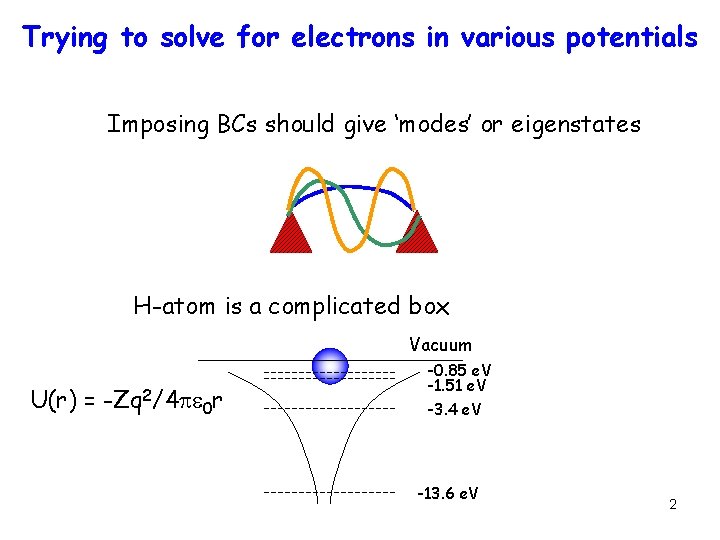
Trying to solve for electrons in various potentials Imposing BCs should give ‘modes’ or eigenstates H-atom is a complicated box Vacuum U(r) = -Zq 2/4 pe 0 r -0. 85 e. V -1. 51 e. V -3. 4 e. V -13. 6 e. V 2

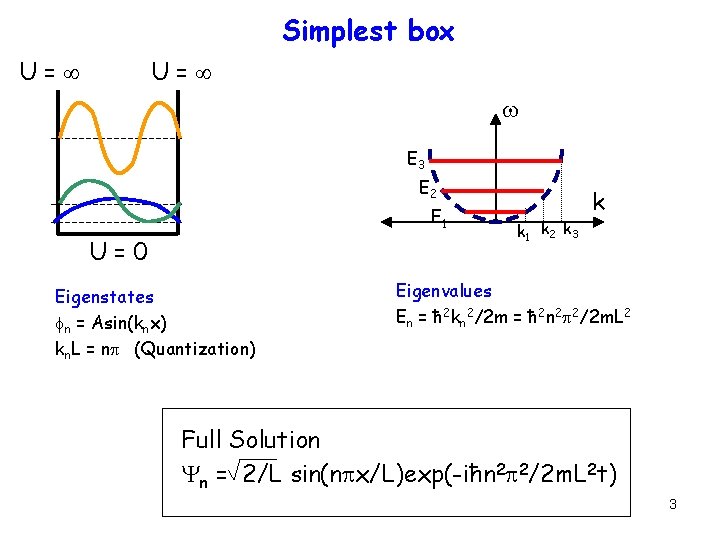
Simplest box U= w E 3 E 2 E 1 U=0 Eigenstates fn = Asin(knx) kn. L = np (Quantization) k 1 k 2 k 3 k Eigenvalues En = ħ 2 kn 2/2 m = ħ 2 n 2 p 2/2 m. L 2 Full Solution Yn = 2/L sin(npx/L)exp(-iħn 2 p 2/2 m. L 2 t) 3

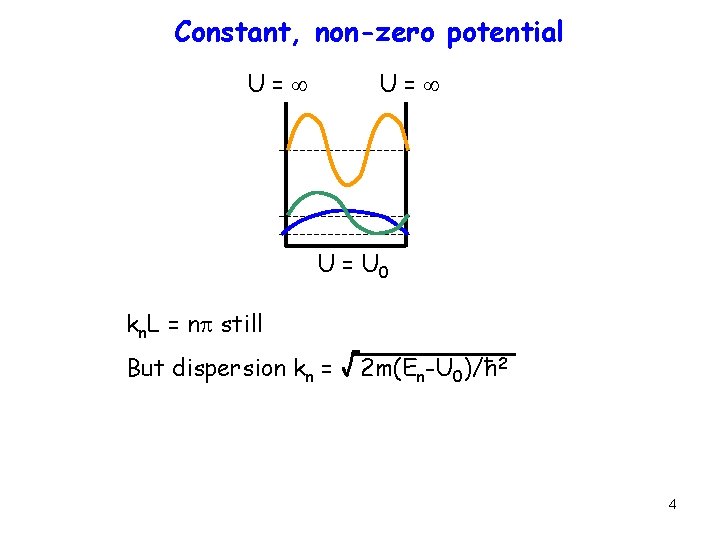
Constant, non-zero potential U= U = U 0 kn. L = np still But dispersion kn = √ 2 m(En-U 0)/ħ 2 4

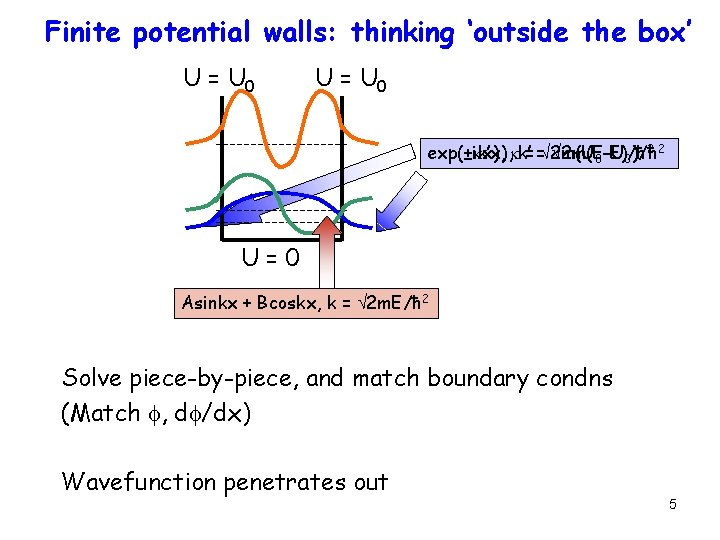
Finite potential walls: thinking ‘outside the box’ U = U 0 22 exp(±ik’x), kk’= = 2 m(U exp(±kx), 2 m(E-U 0 -E)/ħ 0)/ħ U=0 Asinkx + Bcoskx, k = 2 m. E/ħ 2 Solve piece-by-piece, and match boundary condns (Match f, df/dx) Wavefunction penetrates out 5

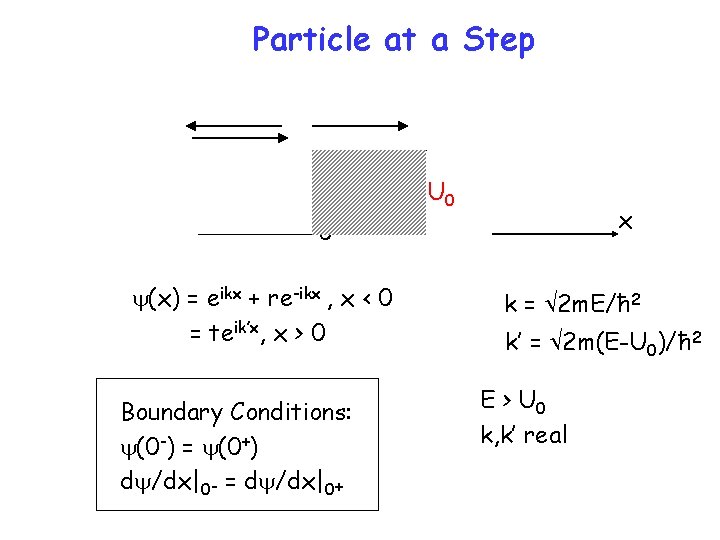
Particle at a Step U 0 x 0 y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 Boundary Conditions: y(0 -) = y(0+) dy/dx|0 - = dy/dx|0+ k = 2 m. E/ħ 2 k’ = 2 m(E-U 0)/ħ 2 E > U 0 k, k’ real

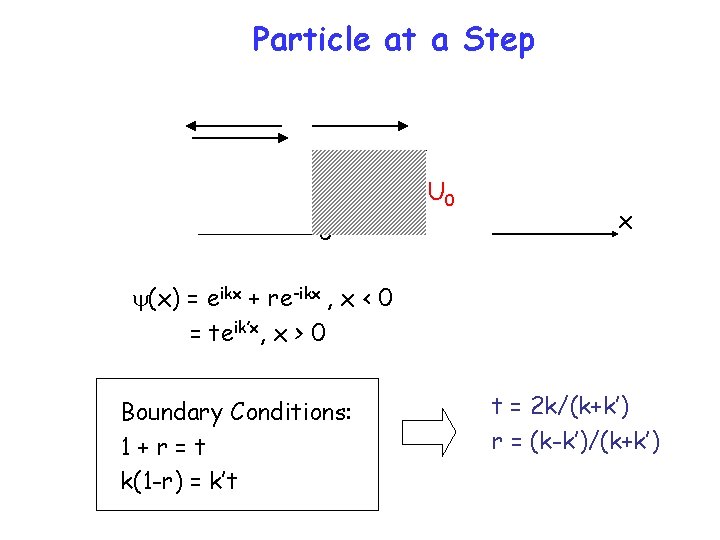
Particle at a Step U 0 0 x y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 Boundary Conditions: 1+r=t k(1 -r) = k’t t = 2 k/(k+k’) r = (k-k’)/(k+k’)

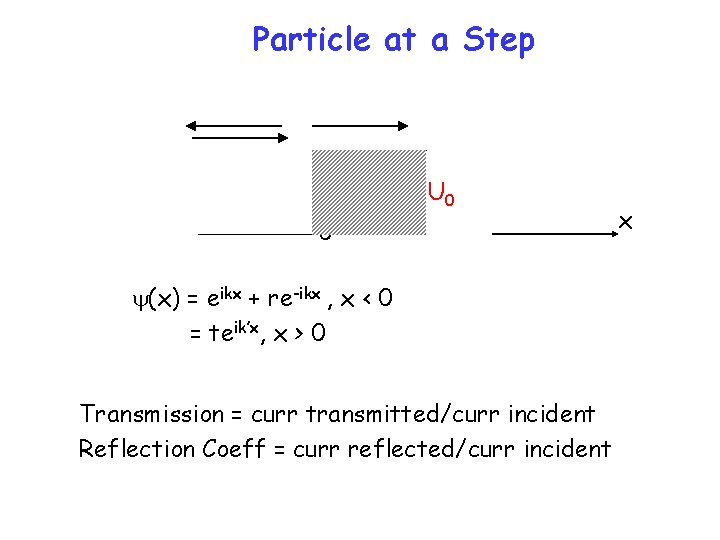
Particle at a Step U 0 0 y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 Transmission = curr transmitted/curr incident Reflection Coeff = curr reflected/curr incident x

Particle at a Step U 0 0 y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 Free particle J = ħk/m|y 0|2, y 0: amplitude (More correctly, J = Re(ħk/m|y 0|2), in case k is complex) Thus, T = Re(k’|t|2/k), R = |r|2 x

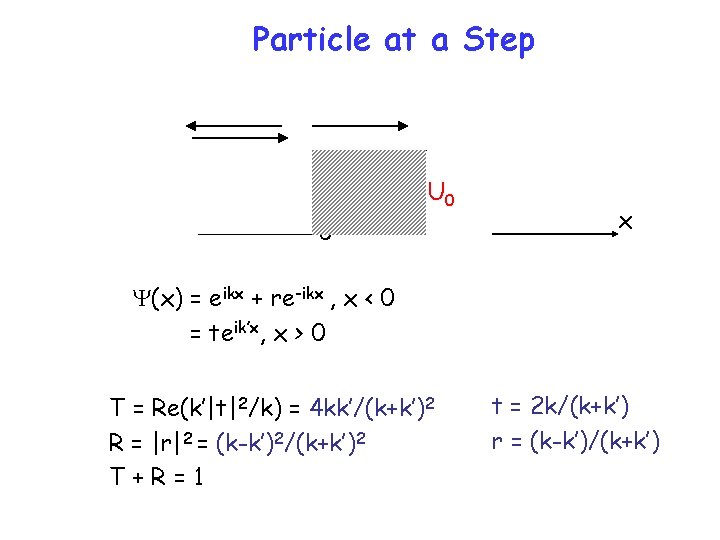
Particle at a Step U 0 0 x Y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 T = Re(k’|t|2/k) = 4 kk’/(k+k’)2 R = |r|2 = (k-k’)2/(k+k’)2 T+R=1 t = 2 k/(k+k’) r = (k-k’)/(k+k’)

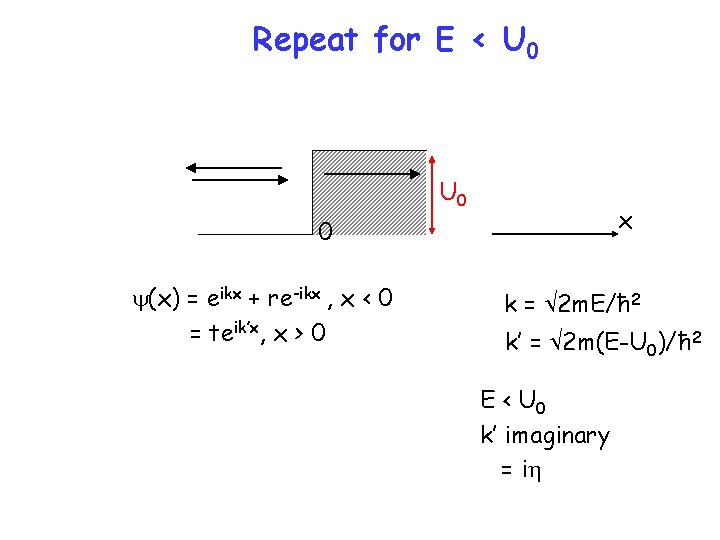
Repeat for E < U 0 x 0 y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 k = 2 m. E/ħ 2 k’ = 2 m(E-U 0)/ħ 2 E < U 0 k’ imaginary = ih

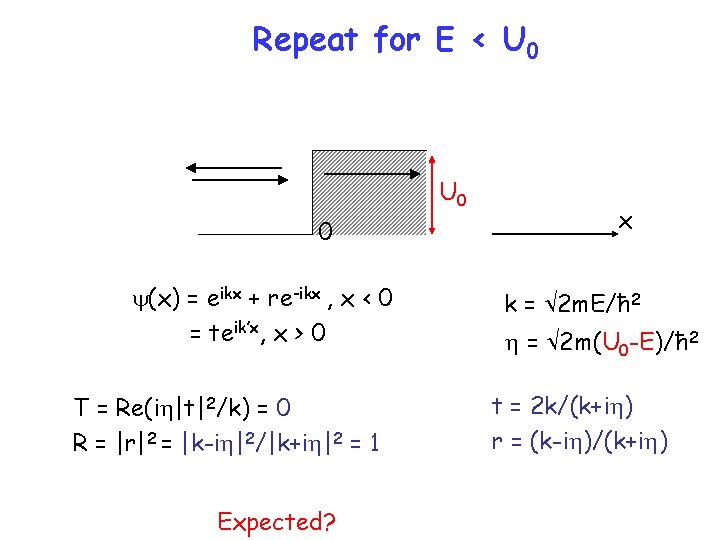
Repeat for E < U 0 0 y(x) = eikx + re-ikx , x < 0 = teik’x, x > 0 T = Re(ih|t|2/k) = 0 R = |r|2 = |k-ih|2/|k+ih|2 = 1 Expected? x k = 2 m. E/ħ 2 h = 2 m(U 0 -E)/ħ 2 t = 2 k/(k+ih) r = (k-ih)/(k+ih)

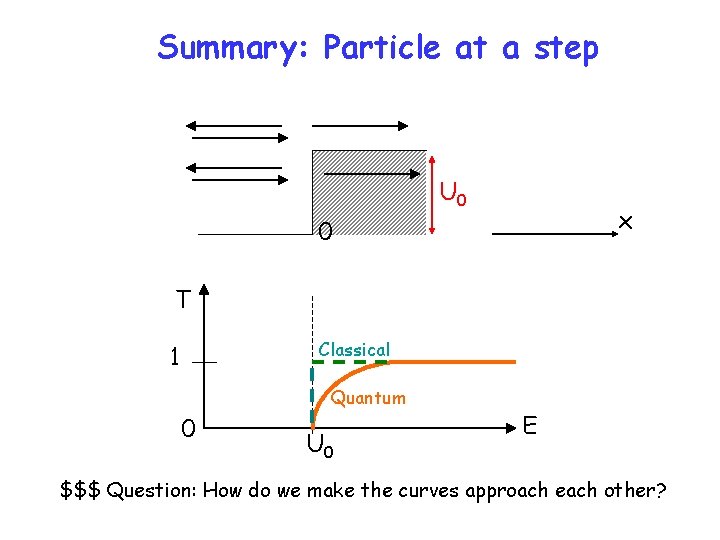
Summary: Particle at a step U 0 x 0 T Classical 1 Quantum 0 U 0 E $$$ Question: How do we make the curves approach each other?

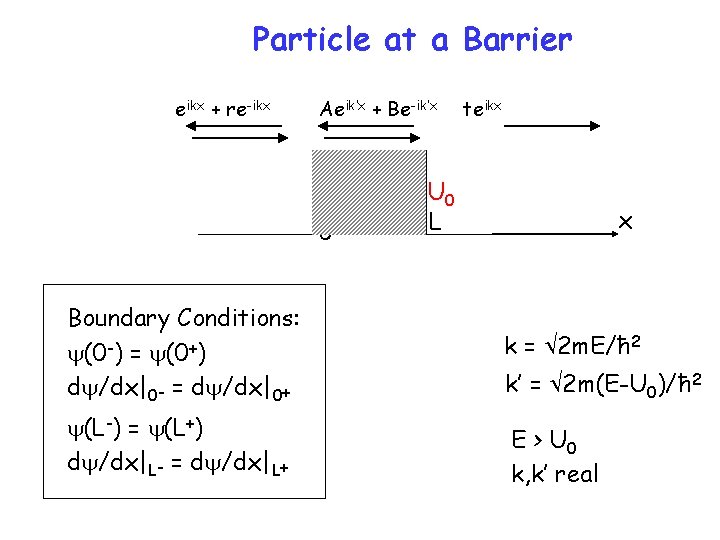
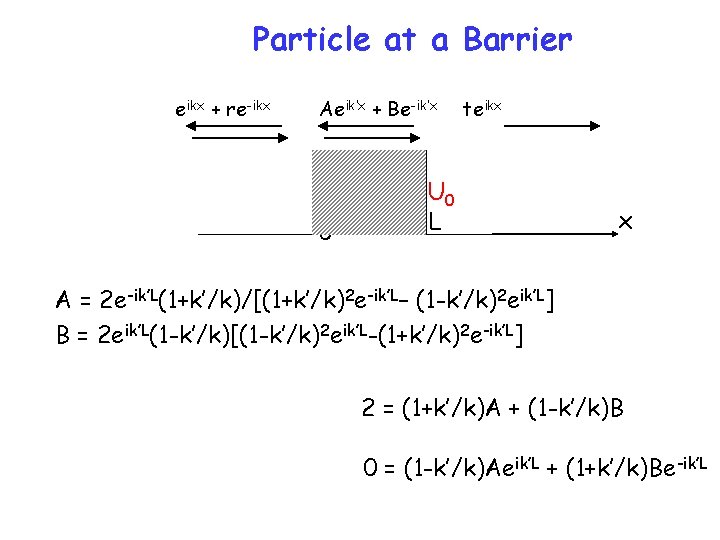
Particle at a Barrier eikx + re-ikx Aeik’x + Be-ik’x 0 teikx U 0 L x Boundary Conditions: y(0 -) = y(0+) dy/dx|0 - = dy/dx|0+ k = 2 m. E/ħ 2 y(L-) = y(L+) dy/dx|L- = dy/dx|L+ E > U 0 k, k’ real k’ = 2 m(E-U 0)/ħ 2

Particle at a Barrier eikx + re-ikx Aeik’x + Be-ik’x 0 1+ r = A + B k(1 -r) = k’(A-B) Aeik’L + Be-ik’L = teik. L k’(Aeik’L – Be-ik’L) = kteik. L U 0 L teikx x 2 = (1+k’/k)A + (1 -k’/k)B 0 = (1 -k’/k)Aeik’L + (1+k’/k)Be-ik’L

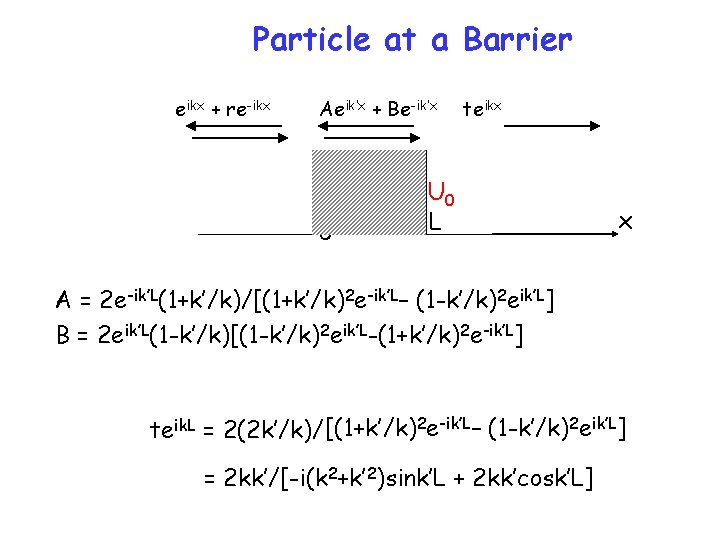
Particle at a Barrier eikx + re-ikx Aeik’x + Be-ik’x 0 teikx U 0 L x A = 2 e-ik’L(1+k’/k)/[(1+k’/k)2 e-ik’L– (1 -k’/k)2 eik’L] B = 2 eik’L(1 -k’/k)[(1 -k’/k)2 eik’L-(1+k’/k)2 e-ik’L] 2 = (1+k’/k)A + (1 -k’/k)B 0 = (1 -k’/k)Aeik’L + (1+k’/k)Be-ik’L

Particle at a Barrier eikx + re-ikx Aeik’x + Be-ik’x 0 teikx U 0 L x A = 2 e-ik’L(1+k’/k)/[(1+k’/k)2 e-ik’L– (1 -k’/k)2 eik’L] B = 2 eik’L(1 -k’/k)[(1 -k’/k)2 eik’L-(1+k’/k)2 e-ik’L] teik. L = 2(2 k’/k)/ [(1+k’/k)2 e-ik’L– (1 -k’/k)2 eik’L] = 2 kk’/[-i(k 2+k’ 2)sink’L + 2 kk’cosk’L]

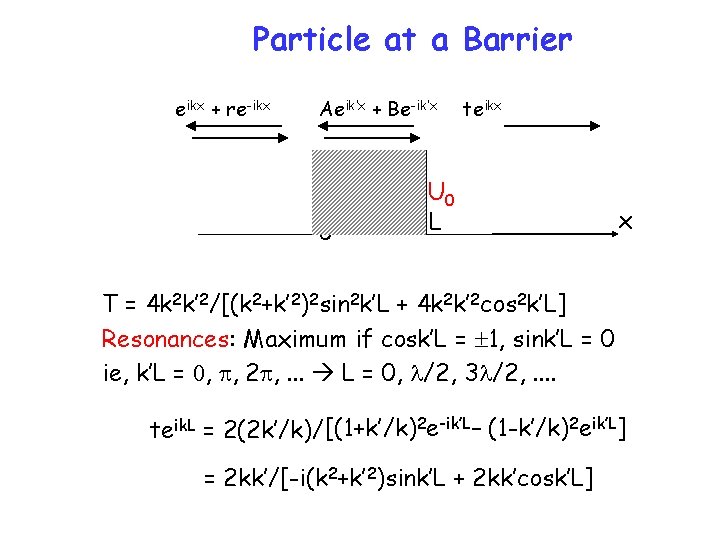
Particle at a Barrier eikx + re-ikx Aeik’x + Be-ik’x 0 teikx U 0 L x T = 4 k 2 k’ 2/[(k 2+k’ 2)2 sin 2 k’L + 4 k 2 k’ 2 cos 2 k’L] Resonances: Maximum if cosk’L = 1, sink’L = 0 ie, k’L = 0, p, 2 p, . . . L = 0, l/2, 3 l/2, . . teik. L = 2(2 k’/k)/ [(1+k’/k)2 e-ik’L– (1 -k’/k)2 eik’L] = 2 kk’/[-i(k 2+k’ 2)sink’L + 2 kk’cosk’L]

More obvious if it’s a well eikx + re-ikx Aeik’x + Be-ik’x 0 teikx U 0 L ie, k’L = 0, p, 2 p, . . . L = 0, l/2, 3 l/2, . . Represent Resonances, with E > U 0 (They would be bound states if E < U 0) Here k = 2 m(E-U 0)/ħ 2 k’ = 2 m. E/ħ 2 x

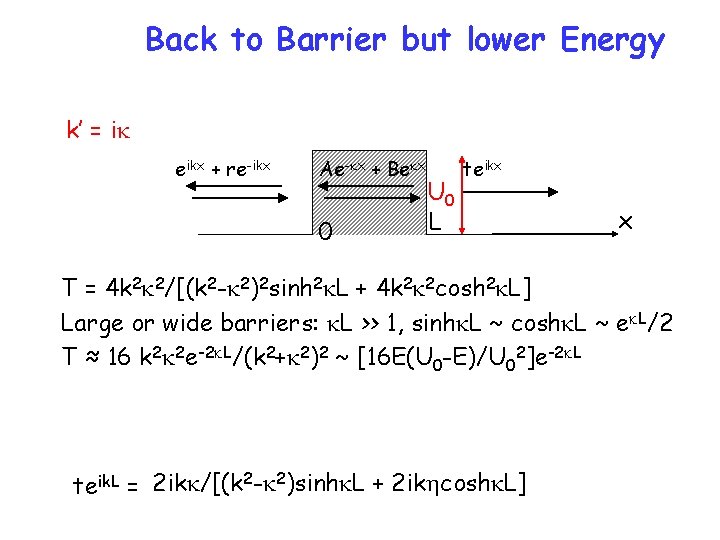
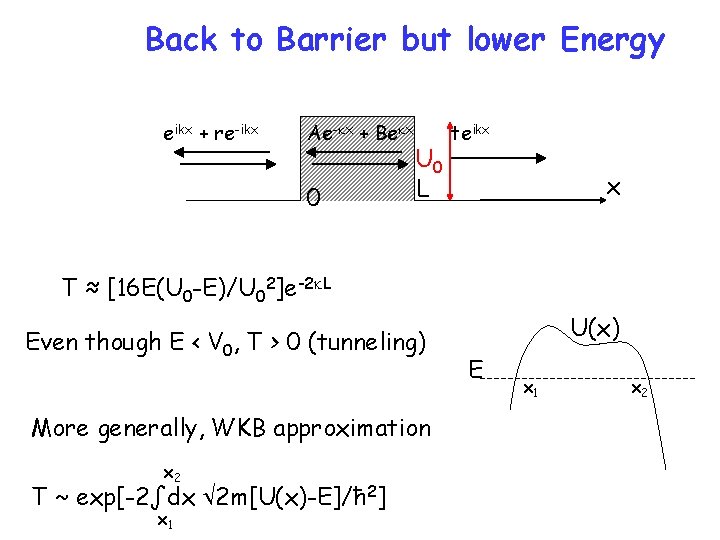
Back to Barrier but lower Energy k’ = ik eikx + re-ikx Ae-kx + Bekx 0 U 0 L teikx x T = 4 k 2 k 2/[(k 2 -k 2)2 sinh 2 k. L + 4 k 2 k 2 cosh 2 k. L] Large or wide barriers: k. L >> 1, sinhk. L ~ coshk. L ~ ek. L/2 T ≈ 16 k 2 k 2 e-2 k. L/(k 2+k 2)2 ~ [16 E(U 0 -E)/U 02]e-2 k. L teik. L = 2 ikk/[(k 2 -k 2)sinhk. L + 2 ikhcoshk. L]

Back to Barrier but lower Energy eikx + re-ikx Ae-kx + Bekx 0 U 0 L teikx x T ≈ [16 E(U 0 -E)/U 02]e-2 k. L Even though E < V 0, T > 0 (tunneling) More generally, WKB approximation x 2 T ~ exp[-2∫dx 2 m[U(x)-E]/ħ 2] x 1 U(x) E x 1 x 2

Example: Tunneling x 2 T ~ exp[-2∫dx 2 m[U(x)-E]/ħ 2] x 1 Well Barrier • • Alpha particle decay from nucleus Source-Drain tunneling in MOSFETs Single Electron Tunneling Devices (SETs) Resonant Tunneling Devices (RTDs)

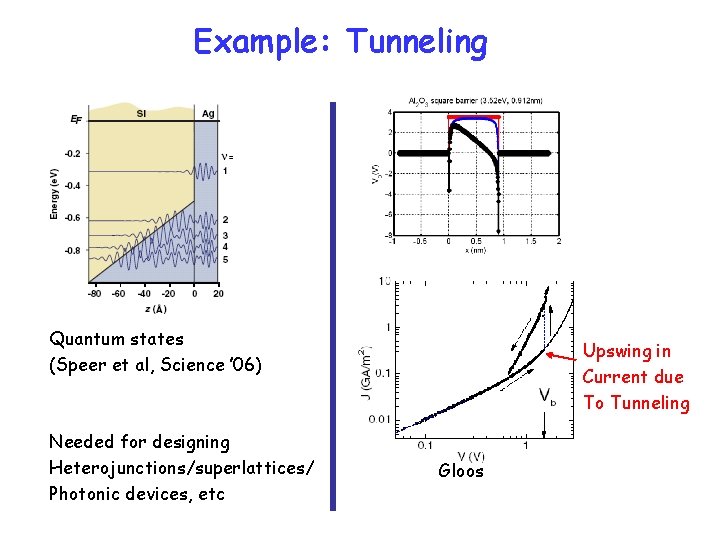
Example: Tunneling Quantum states (Speer et al, Science ’ 06) Needed for designing Heterojunctions/superlattices/ Photonic devices, etc Upswing in Current due To Tunneling Gloos

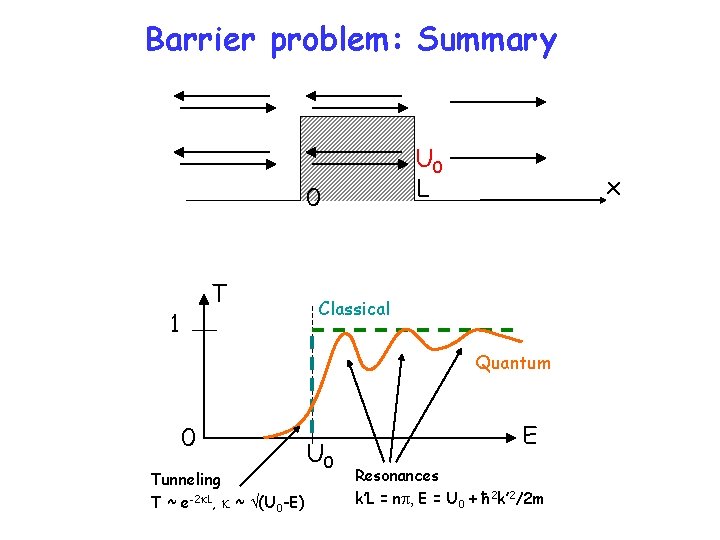
Barrier problem: Summary U 0 L 0 T 1 x Classical Quantum 0 Tunneling T ~ e-2 k. L, k ~ (U 0 -E) U 0 E Resonances k’L = np, E = U 0 + ħ 2 k’ 2/2 m