The Standard Normal Distribution Standard Normal Distribution What

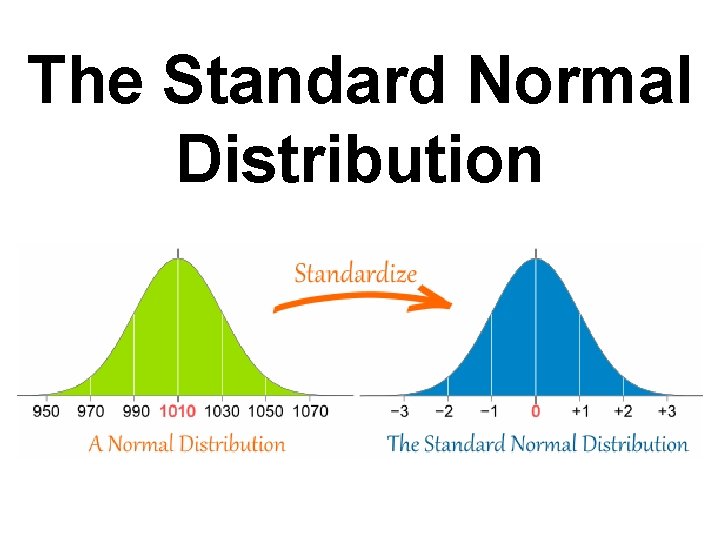
The Standard Normal Distribution

Standard Normal Distribution What does this mean? The shape of the normal curve depends on the values of the mean, and the standard deviation. To save time calculating probabilities for every combination, the curve is standardized; mean becomes 0 (μ=0) standard deviation becomes 1 (σ=1) Special tables provide probabilities for a Standard Normal Curve.

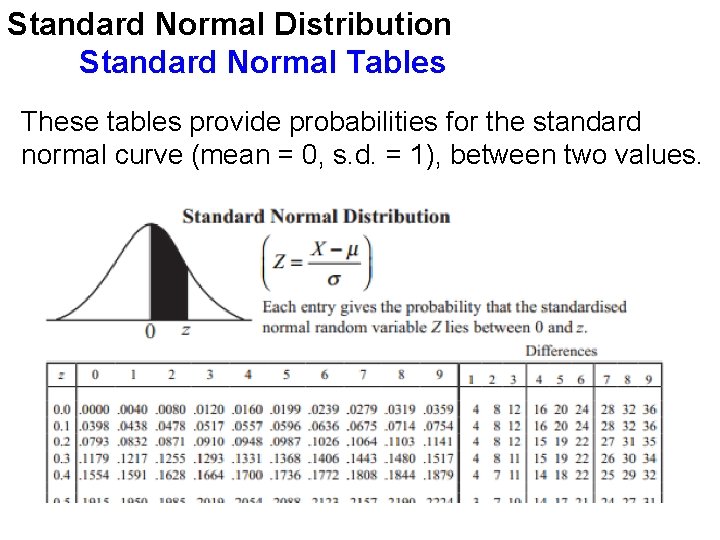
Standard Normal Distribution Standard Normal Tables These tables provide probabilities for the standard normal curve (mean = 0, s. d. = 1), between two values.

Standard Normal Distribution What is a ‘z’ value? For a standardised normal distribution, the ‘z’ value refers to the number of standard deviations away from the mean. i. e. a z value of 0. 8 means that X is 0. 8 standard deviations away from the mean.

Standard Normal Distribution Standard Normal Tables These tables give the area under the Standard Normal curve between 0 and a value ‘z’. This area is equal to the probability of a value lying between 0 and z. Example Find the probability that Z lies between 0 and 1. 9. i. e. P(0 < Z < 1. 9) The area shaded = 0. 4713 (from tables)

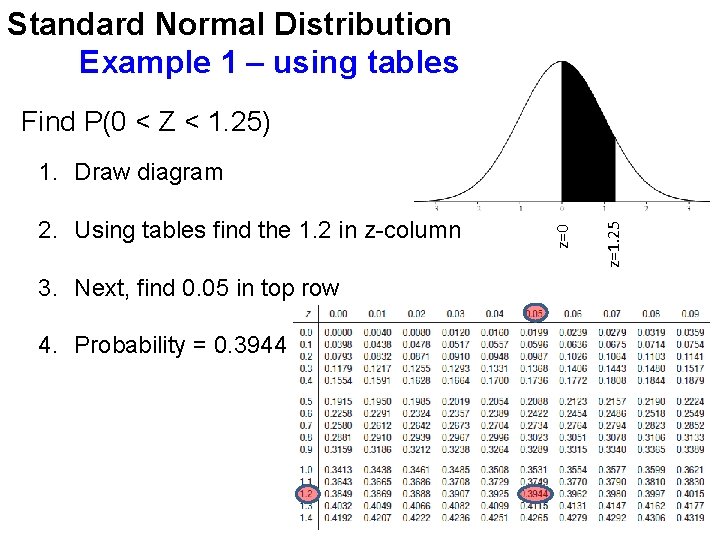
Standard Normal Distribution Example 1 – using tables Find P(0 < Z < 1. 25) 3. Next, find 0. 05 in top row 4. Probability = 0. 3944 z=1. 25 2. Using tables find the 1. 2 in z-column z=0 1. Draw diagram

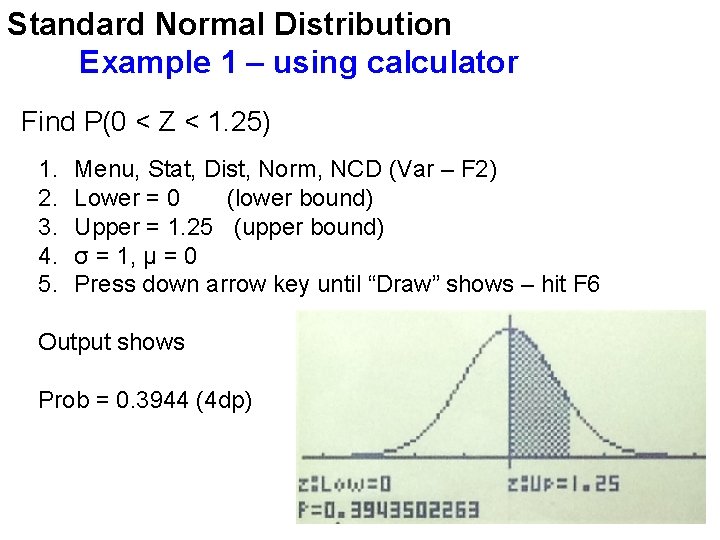
Standard Normal Distribution Example 1 – using calculator Find P(0 < Z < 1. 25) 1. 2. 3. 4. 5. Menu, Stat, Dist, Norm, NCD (Var – F 2) Lower = 0 (lower bound) Upper = 1. 25 (upper bound) σ = 1, μ = 0 Press down arrow key until “Draw” shows – hit F 6 Output shows Prob = 0. 3944 (4 dp)

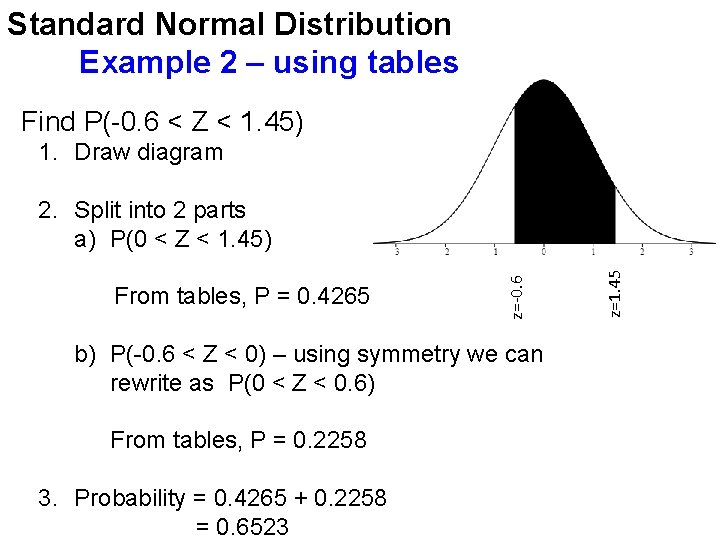
Standard Normal Distribution Example 2 – using tables Find P(-0. 6 < Z < 1. 45) 1. Draw diagram b) P(-0. 6 < Z < 0) – using symmetry we can rewrite as P(0 < Z < 0. 6) From tables, P = 0. 2258 3. Probability = 0. 4265 + 0. 2258 = 0. 6523 z=1. 45 From tables, P = 0. 4265 z=-0. 6 2. Split into 2 parts a) P(0 < Z < 1. 45)

Standard Normal Distribution Example 2 – using calculator Find P(-0. 6 < Z < 1. 45) 1. 2. 3. 4. 5. Menu, Stat, Dist, Norm, NCD Lower = -0. 6 (lower bound) Upper = 1. 45 (upper bound) σ = 1, μ = 0 Press down arrow key until “Draw” shows – hit F 6 Output shows Prob = 0. 6522 (4 dp)