The Stale of a System Is Completely Specified

















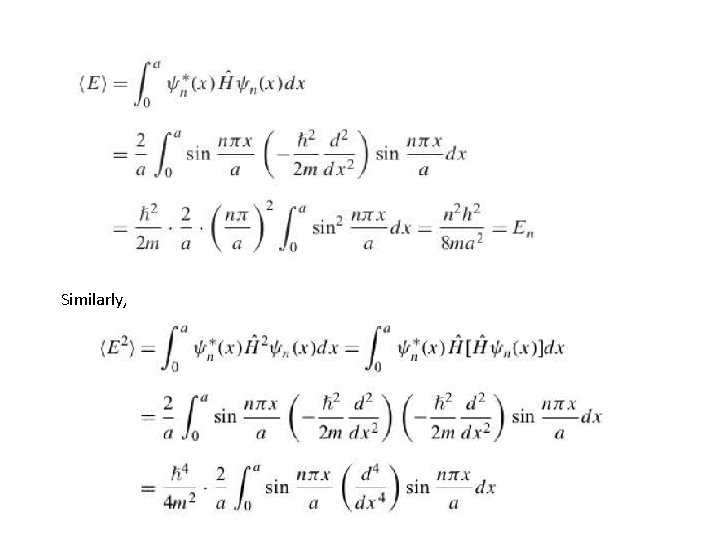






















- Slides: 41

The Stale of a System Is Completely Specified by lts Wave Function Ø Classical mechanics deals with quantities called dynamical variables, such as position, momentum, angular momentum, and energy. Ø A measurable dynamical variable is called an observable. Ø The classical-mechanical state of a one-body system at any particular time is specified completely by the three position coordinates (x, y, z) and the three momenta or velocities ( x , y , z ) at that time.

The Postulates and General Principles of Quantum Mechanics Postulate 1 The state of a quantum-mechanical system is completely specified by a function (r, t) that depends on the coordinates of the particle and on time. This function, called the wave function or state function, has the important property that *(r, t)dxdydz is the probability that the particle lies in the volume element dxdydz located at r at time t. Ø If there is more than one particle, say two, then we write

Because the square of the wave function has a probabilistic interpretation, it must satisfy certain physical requirements. For example, a wave function must be normalized, so that in the case of one particle, for simplicity, we have

We let n x /a be z

and thus the above wave functions are normalized. In addition to being normalized, or at least normalizable, we require that (r, t) and its first spatial derivative be single-valued, continuous, and finite. We summarize these requirements by saying that (r, t) must be well behaved.



In quantum mechanics, we deal only with linear operators. An operator is said to be linear if where c 1 and c 2 are (possibly complex) constants. Clearly, the "differentiate" and "integrate" operators are linear because and The "square" operator, SQR, on the other hand, is nonlinear because

Postulate 2 To every observable in classical mechanics there corresponds a linear operator in quantum mechanics. Consider an eigenvalue problem with a two-fold degeneracy

Classical-Mechanical Observables and Their Corresponding Quantum. Mechanical Operators



Generally, an operator will have a set of eigenfunctions and eigenvalues, and we indicate this by writing

As a specific example, consider the measurement of the energy. The operator corresponding to the energy is the Hamiltonian operator, and its eigenvalue equation is


SOLUTION: The normalization integral of (x) is elementary:

In other words, show that the only values of the energy that can be observed are the energy eigenvalues, SOLUTION: The operator that corresponds to the observable Eis the Hamiltonian operator, which for a particle in a box is The average energy is given by
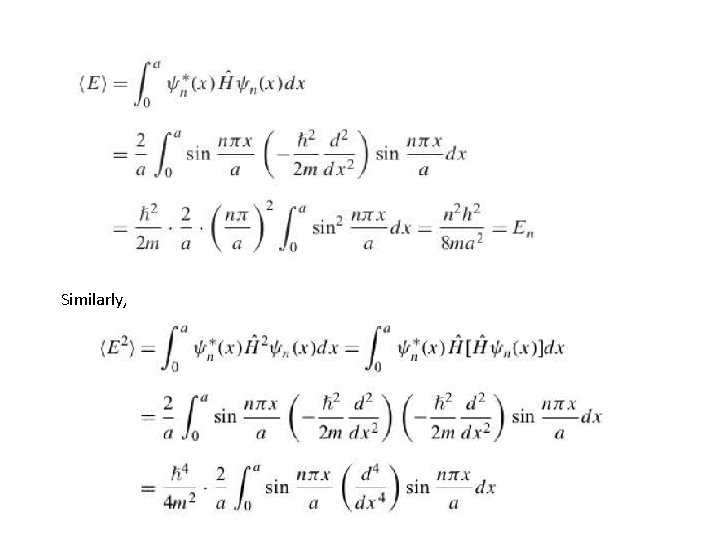
Similarly,

The Commutator of Two Operators

if For example





If two operators do not commute, then their corresponding observable quantities do not have simultaneously well-defined values Quantum-Mechanical Operators Must Be Hermitian Operators In an equation, we have multiply from the left by * and integrate to obtain

take the complex conjugate of Equation where the equality a* = a recognizes that a is real. Multiply from the left by and integrate Equating the left sides of Equations 4. 25 and 4. 27 gives The operator A must satisfy Equation 4. 28 to assure that its eigenvalues are real. An operator that satisfies Equation 4. 28 for any well-behaved function is called a Hermitian operator. Thus, we can write the definition of a Hermitian operator as an operator that satisfies the relation

Eq. 1 Postulate 1’ To every observable in classical mechanics there corresponds a linear; Hermitian operator in quantum mechanics. Consider the operator A = d / dx. Does A satisfy Equation 4. 29? Let's substitute A = d/ dx into Equation 4. 29 and integrate by parts:

For a wave function to be normalizable, it must vanish at infinity, and so the first term on the right side here is zero. Therefore, we have For an arbitrary function f (x), d/dx does not satisfy Equation 4. 29 and so is not Hermitian.


Thus, Equation 4. 29 is satisfied, and the kinetic energy operator is Hermitian.

Consider the two eigenvalue equations We multiply the first of Equations by m*, and integrate then we take the complex conjugate of the second, multiply by n, and integrate to obtain

By subtracting Equations, we obtain Because A is Hermitian When n = m, the integral is unity by normalization and so we have Now if the system is nondegenerate, and

A set of eigenfunctions that satisfies the condition in Equation 4. 42 is said to be orthogonal. The particle in a box is a nondegenerate system. The wave functions for this system are

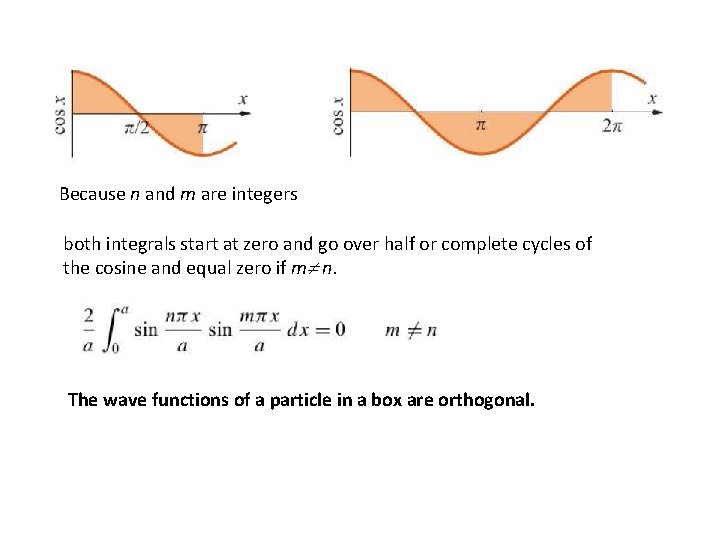
Because n and m are integers both integrals start at zero and go over half or complete cycles of the cosine and equal zero if m n. The wave functions of a particle in a box are orthogonal.

When n = m in Equation cos 0 = 1, The second integral on the right side vanishes and so we have

A set of functions that are both normalized and orthogonal to each other is called an orthonormal set. We can express the condition of orthonormality by writing The symbol nm occurs frequently and is called the Kronecker delta The eigenfunctions of a particle constrained to move on a circular ring of radius a are


Suppose that two operators A and B have the same set of eigenfunctions, so that we have Equations 4. 50 imply that the quantities corresponding to A and B have simultaneously sharply defined values. According to Equations 4. 50, the values that we observe are an and bn. if two operators have the same set of eigenfunctions, then they necessarily commute.

Postulate 5 The wave function or state function of a system evolves in time according to the timedependent Schrodinger equation H does not contain time explicitly, and in this case we can apply the method of separation of variables and write

If H does not contain time explicitly, then the left side of Equation 4. 70 is a function of x only and the right side is a function oft only, and so both sides must equal a constant. If we denote the separation constant by E , then Equation 4. 70 gives time-independent Schrodinger equation
