The stabilizing token ring in three bits Mohamed

The stabilizing token ring in three bits Mohamed G. Gouda F. Furman Haddix Presented by: Marc Segal

Self-stabilizing Systems • States of a system are partitioned into legal illegal states • Every state that is reachable from a legal state is legal • The system is stabilizing iff starting from any state the system will reach a legal state in a finite number of state transitions. Illegal states Legal states

Unidirectional Stabilizing Token Rings • The legal states: – there is exactly one token • The illegal states: – No token exists – There is more than one token T T T

Unidirectional Stabilizing Token Rings • The legal states: – there is exactly one token • The illegal states: – No token exists – There is more than one token T T T

Reminder: Dijkstra’s algorithm • Dijkstra presented three algorithms for a selfstabilizing token ring: – Dijkstra’s 1 st algorithm : every processor is a k-state machine, k>N-2 – Dijkstra’s 2 nd algorithm : 4 states – Dijkstra’s 3 rd algorithm : 3 states • However, Dijkstra’s 2 nd & 3 rd algorithms are bidirectional. • Is there a deterministic self-stabilizing token ring algorithm that uses less states ? • Particularly, is there a deterministic selfstabilizing token ring algorithm that uses a number of states that is not dependent on the number of processors ?

A 1 -bit algorithm ? • Let’s attempt to design a 1 -bit self-stabilizing token ring algorithm • We would like the algorithm to: – Create a new token when there is no circulating token – Reduce the number of tokens when there is more than one token – Be fair: the token must circulate • Some Notations: – – Every process has a boolean state variable t. We denote the variable t of process Pi by t. i is can be read and written by process Pi t. i can be read by process Pi+1

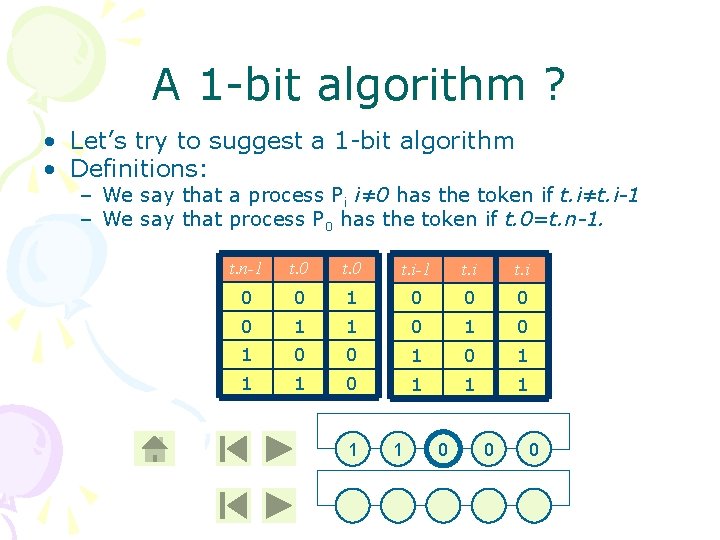
A 1 -bit algorithm ? • Let’s try to suggest a 1 -bit algorithm • Definitions: – We say that a process Pi i≠ 0 has the token if t. i≠t. i-1 – We say that process P 0 has the token if t. 0=t. n-1 t. 0 t. i-1 t. i 0 0 1 1 0 1 0 0 1 1 1 0 0 0

A 1 -bit algorithm ? • By defining token possession differently for P 0 and the other processes we ensure that there will always be at least one token. • But what about multiple tokens ? How do we reduce the number of tokens? • Let’s differentiate between two types of tokens: – If a process Pi has a token and t. i=true we say that it has a T-token. – If a process Pi has a token and t. i=false we say that it has an F-token. • Our goal is to allow T-tokens to move freely, while limiting the movement of F-tokens

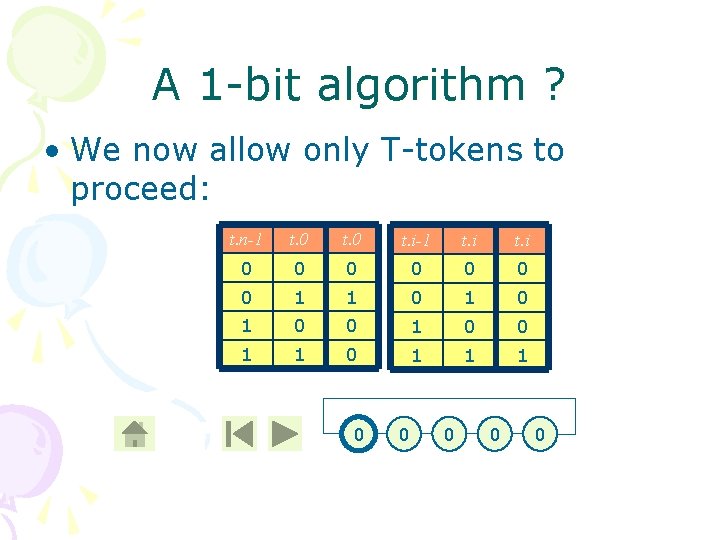
A 1 -bit algorithm ? • We now allow only T-tokens to proceed: t. n-1 t. 0 t. i-1 t. i 0 0 0 0 1 1 0 1 1 1 0 0 0

A 2 -bit algorithm? • We’d still like F-tokens to be able to proceed, only slower than T-tokens. • We introduce a new state variable: ready. • A node can pass an F-token to its neighbor only if it its ready variable is true. • If a node has an F-token and its ready variable is false, it turns it on.

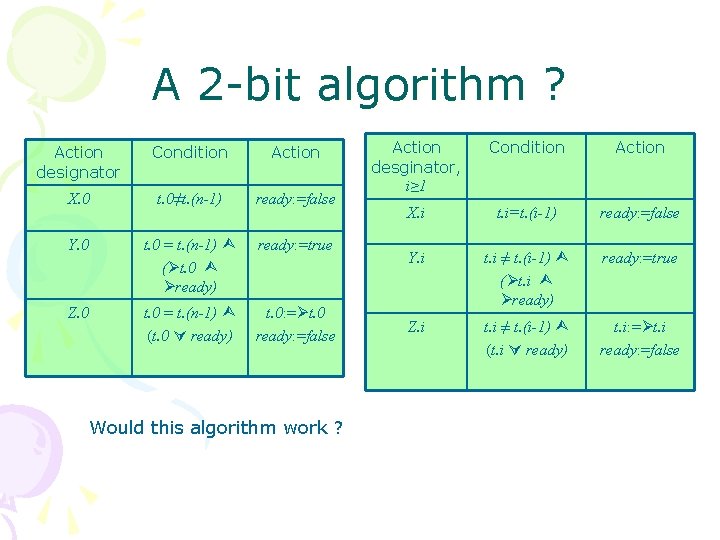
A 2 -bit algorithm ? Action designator Condition Action X. 0 t. 0≠t. (n-1) ready: =false Y. 0 t. 0 = t. (n-1) ( t. 0 ready) ready: =true Z. 0 t. 0 = t. (n-1) (t. 0 ready) t. 0: = t. 0 ready: =false Would this algorithm work ? Action desginator, i≥ 1 Condition Action X. i t. i=t. (i-1) ready: =false Y. i t. i ≠ t. (i-1) ( t. i ready) ready: =true Z. i t. i ≠ t. (i-1) (t. i ready) t. i: = t. i ready: =false

2 -bit Algorithm Operation Simulation P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 P 9 t ready Reset P 0 P 1 Set P 2 F Next P 3 P 4 P 5 P 6 P 7 P 8 P 9

2 -bit algorithm conclusions • An F-token must execute two actions each time it proceeds from one process to the next. • A T-token needs only execute one. • This doesn't work ! • The scheduler may allow processes that hold F-tokens to execute two actions, for each action it allows a process that holds a T-token. • What schduler would this algorithm work with ?

The 3 -bits algorithm Definitions • Every process has three boolean variables: – e – determines if the process has an enabler – t – determines if the process has a token – ready • A process can make a move only if it has an enabler. – Process P 0 has an enabler if e. 0=e. (n-1) – Process Pi , i≠ 0 has an enabler if e. i≠e. (n-1) • Similiarly: – Process P 0 has a token if t. 0=t. (n-1) – Process Pi , i≠ 0 has a token if t. i≠t. (n-1) • If a process Pi has a token and t. i=true we say that it has a T -token. • If a process Pi has a token and t. i=false we say that it has an F-token.

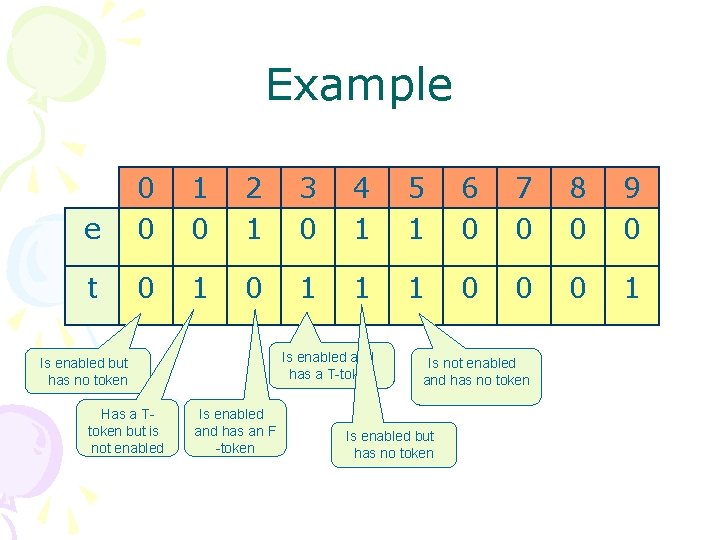
Example e 0 0 1 0 2 1 3 0 4 1 5 1 6 0 7 0 8 0 9 0 t 0 1 1 1 0 0 0 1 Is enabled and has a T-token Is enabled but has no token Has a Ttoken but is not enabled Is enabled and has an F -token Is not enabled and has no token Is enabled but has no token

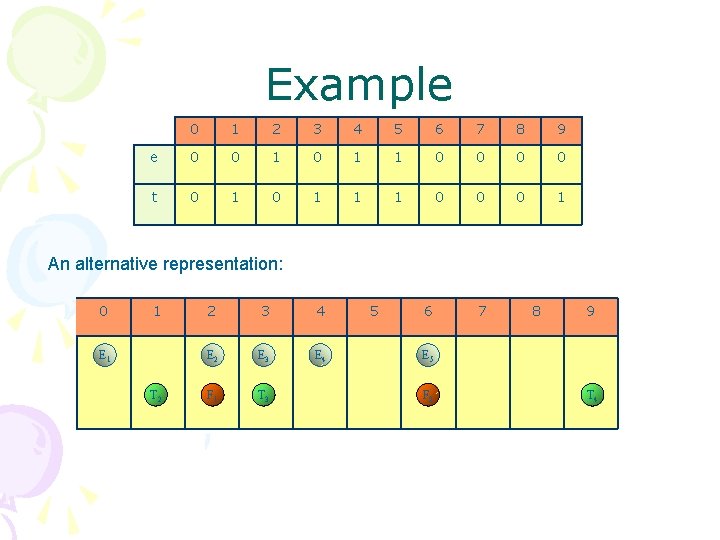
Example 0 1 2 3 4 5 6 7 8 9 e 0 0 1 1 0 0 t 0 1 1 1 0 0 0 1 An alternative representation: 0 1 E 1 T 2 2 3 4 E 2 E 3 E 4 F 1 T 3 5 6 7 8 9 E 5 F 2 T 4

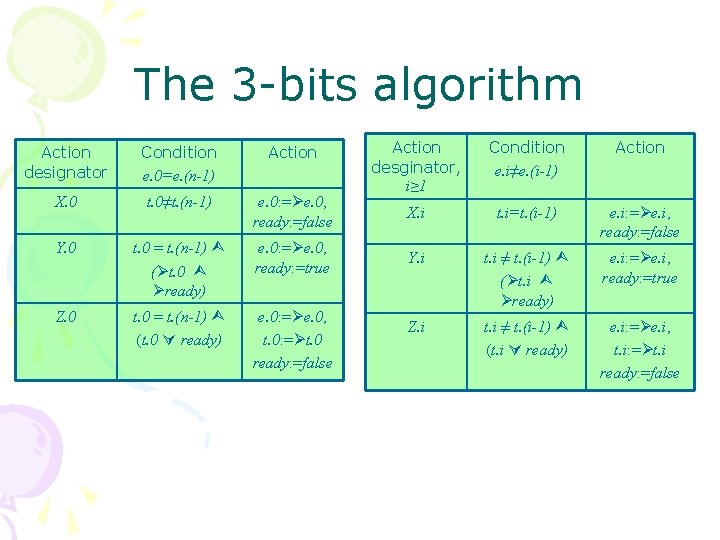
The 3 -bits algorithm Action designator Condition e. 0=e. (n-1) Action X. 0 t. 0≠t. (n-1) e. 0: = e. 0, ready: =false Y. 0 t. 0 = t. (n-1) ( t. 0 ready) e. 0: = e. 0, ready: =true Z. 0 t. 0 = t. (n-1) (t. 0 ready) e. 0: = e. 0, t. 0: = t. 0 ready: =false Action desginator, i≥ 1 Condition e. i≠e. (i-1) Action X. i t. i=t. (i-1) e. i: = e. i, ready: =false Y. i t. i ≠ t. (i-1) ( t. i ready) e. i: = e. i, ready: =true Z. i t. i ≠ t. (i-1) (t. i ready) e. i: = e. i, t. i: = t. i ready: =false

The 3 -bits algorithm Action designator Condition Action X. i has enabler & doesn’t have token pass enabler ready: =false Y. i has enabler & has an F-token & ready pass enabler ready: =true Z. i has enabler & (has a T-token or (has an F-token and ready=true) ) pass enabler pass token ready: =false

The 3 -bits algorithm Action designator Condition Action X. i has enabler & doesn’t have token pass enabler ready: =false Y. i has enabler & has an F-token & ready pass enabler ready: =true Z. i has enabler & (has a T- token or (has an F token and ready=true) ) pass enabler pass token ready: =false • An X action allows the enabler to pass from process Pi to process Pi+1 when Pi does not have a token • A Y action allows the enabler to pass from process Pi to process Pi+1 when Pi has an Ftoken and its variable ready is false. The variable ready becomes true in this action. • A Z action allows the enabler to pass from process Pi to process Pi+1 when Pi has an Ftoken and its variable ready is true or when it has a T-token. The variable ready becomes false in this action.

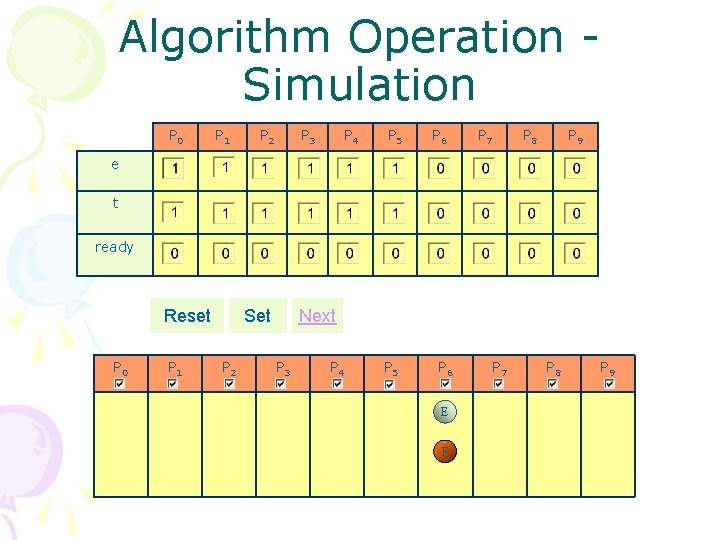
Algorithm Operation Simulation P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 P 9 e t ready Reset P 0 P 1 Set P 2 Next P 3 P 4 P 5 P 6 E F P 7 P 8 P 9

3 -bit Algorithm Observations S H • In every state: • Enablers can proceed freely • T-Tokens can proceed only when they are joined by an enabler. • F-Tokens may only proceed if they are joined by an enabler and the ready flag is not raised – There is at least one enabler – There is at least one token – In every one of the X, Y, Z actions the enabler is passed to the next process – Once a T-Token is joined by an enabler it will “ride” that enabler until it is inverted or annihilated – This is meant to limit the number of hops an F-token rides the enabler to one hop. • Token Inversion • Annihilation: – When a T-token is passed from process Pn-1 to process P 0 it becomes an F-token – When an F-token is passed from process Pn-1 to process P 0 it becomes a T-token – Enabler annihilation occurs when two enablers collide – Token annihilation occurs when two tokens collide – If there is more than one enabler and more than one process makes a move in each step, enabler annihilation may never occur – That is not true for tokens, which is why the algorithm is self stabilizing. . .

Proof of Stabilizaiton S H System Model • Ring state – A state S of the ring is defined by one value for every variable in every process. – A legal state is a state in which there is only one token. • Enabled Process – A Process is enabled if it has an enabler. • Enabled Action • – An action (X, Y or Z) is enabled for a process if the action’s condition is true. – Exactly one action is enabled for each enabled process. Transition – (S, S’) is a transition of the ring if S’ is generated from S by execution a subset of the enabled actions in S. – A distributed scheduler. • Computation – C=S 1 , S 2 , . . . is a computation of the ring if: • Every Si is a state of the ring. • for every pair Si , Si+1 (Si, Si+1) is a transition.

Proof of Stabilization Lemma 1 • • • Definition: We say that a process Pi is e-different if e. i≠e. (i-1) mod n Definition: We say that a process Pi is t-different if t. i≠t. (i-1) mod n Definition: For every state S of an n size ring we define: • Lemma 1: For every state S, Ne-different(S), Nt-different(S) are even e-different 0 1 e-different 1 1 e-different 0 1 S H

Proof of Stabilization S H 0 1 Lemma 1 • • • Definition: We say that a process Pi is e-different if e. i≠e. (i-1) mod n Definition: We say that a process Pi is t-different if t. i≠t. (i-1) mod n Definition: For every state S of an n size ring we define: • Lemma 1: For every state S, Ne-different(S), Nt-different(S) are even 0 1 1 0 1 T 1 1 • If the number of e-different processes in T is even then e. n-1=e. 0 The total number of e-different processes is even • If the number of e-different processes in T is odd then e. n-1≠e. 0 The total number of e-different processes is even

Proof of Stabilization S H Lemma 2 • Definition: For a state S of the ring, we define: • Lemma 2: For every state S or the ring Ntokens(S), Nenablers(S) are odd. • Case 1: Ne-different(S)=0 Only process that has an enabler Nenablers(S)=1 e=0 e=0 e=0

Proof of Stabilization S H Lemma 2 • Definition: For a state S of the ring, we define: • Lemma 2: For every state S of the ring Ntokens(S), Nenablers(S) are odd. • Case 2: Ne-different(S)>0 and P 0 is e-different Is e-different but doesn’t have an enabler e=0 e=0 e=0 e=1 Is e-different and has an enabler e=0 Is e-different and has an enabler Nenablers(S)=Ne-different(S)-1 which is odd by lemma 1 e=0 e=1 Is e-different and has an enabler

Proof of Stabilization S H Lemma 2 • Definition: For a state S of the ring, we define: • Lemma 2: For every state S of the ring Ntokens(S), Nenablers(S) are odd. • Case 3: Ne-different(S)>0 and P 0 is not e-different Is not e-different but has an enabler e=1 e=0 e=0 Is e-different and has an enabler e=1 e=0 Is e-different and has an enabler e=0 e=1 Is e-different and has an enabler Nenablers(S)=Ne-different(S)+1 which is odd by lemma 1

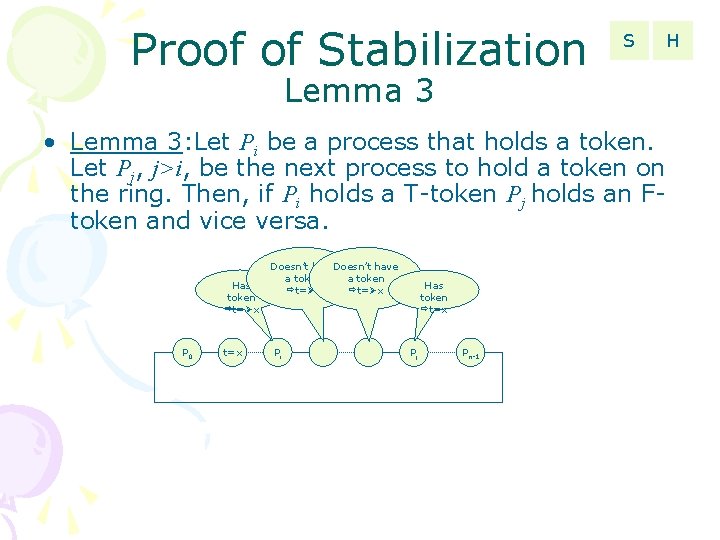
Proof of Stabilization S Lemma 3 • Lemma 3: Let Pi be a process that holds a token. Let Pj, j>i, be the next process to hold a token on the ring. Then, if Pi holds a T-token Pj holds an Ftoken and vice versa. Has token t= x P 0 t=x Doesn’t have a token t= x Pi Has token t=x Pj Pn-1 H

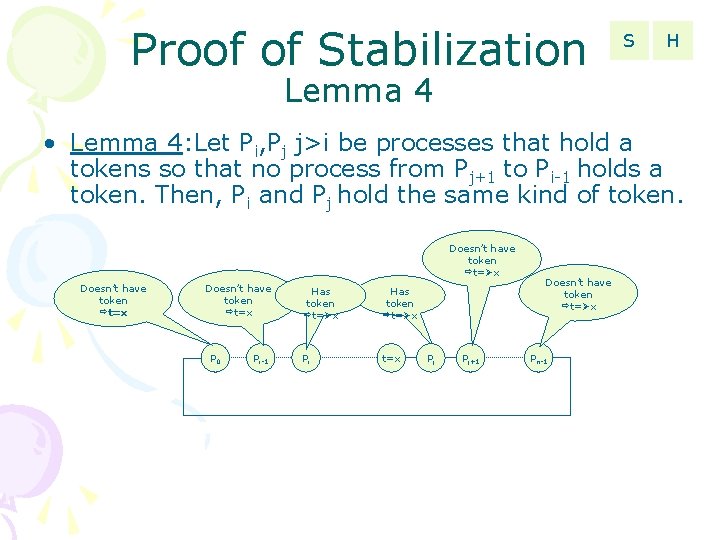
Proof of Stabilization S H Lemma 4 • Lemma 4: Let Pi, Pj j>i be processes that hold a tokens so that no process from Pj+1 to Pi-1 holds a token. Then, Pi and Pj hold the same kind of token. Doesn’t have token t= x Doesn’t have token t=x P 0 Pi-1 Has token t= x Pi t=x Pj Pj+1 Doesn’t have token t= x Pn-1

Proof of Stabilization S Lemma 5 • Lemma 5: For every transition (S, S’): – Nenablers(S’) ≤ Nenablers(S) – Ntokens(S’) ≤ Ntokens(S) Proof: Let Pi be a process that has an enabler in S’ and doesn’t have an enabler in S. Let k be the minimal number for which Pi-k does not execute an action in the transition (S, S’). notan have Doesn’t Must execute an enabler action in (S, S’) in S’ P 0 Pi-k Executes an action Has an action no enabler in S Doesn’t execute in (S, S’) any action in (S, S’) Pi Pn-1 For every process that gains an enabler there is a process that loses an enabler. The proof for tokens is identical. H

Proof of Stabilization S H Lemma 6 • Lemma 6: Every computation of the algorithm is infinite. Proof: A finite computation ends with a state in which no action is enabled. A process that has an enabler in some state has exactly one enabled action. By lemma 2 , the number of enablers in any state is odd. Specifically, the number of enablers cannot be zero.

Proof of Stabilization S H Lemma 7 • Lemma 7: In every computation C, every process has at least one action which is executed infinitely many times. Proof: C is an infinte computation, but the number of processes is finite. There is a process Pi that executes at least one action infinitely many times in C. Assume by contradiction, that Pi-1 executes a finite number of actions in C. Let’s examine a suffix of C in which Pi-1 doesn’t execute any action. e=x Can’t change, no action is executed P 0 Pi-1 In order for Pi to be enabled again must change value of e Eventually is enabled e= x After executing an action e= x=x Pi Contradiction Pn-1

Proof of Stabilization S Lemma 7 • Lemma 7: In every computation C, every process has at least one action which is executed infinitely many times. Proof: For Pi to get enabled again after it executes an action, Pi-1 must execute an action. Pi-1 executes an infinite number of actions. This is true for every Pi, therefore all processes execute infinitely many actions. H

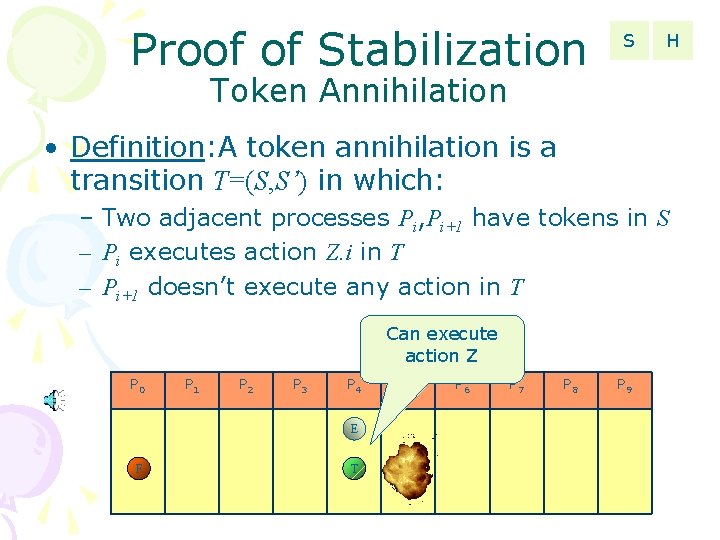
Proof of Stabilization S H Token Annihilation • Definition: A token annihilation is a transition T=(S, S’) in which: – Two adjacent processes Pi, Pi+1 have tokens in S – Pi executes action Z. i in T – Pi+1 doesn’t execute any action in T Can execute action Z P 0 P 1 P 2 P 3 P 4 P 5 E F T F P 6 P 7 P 8 P 9

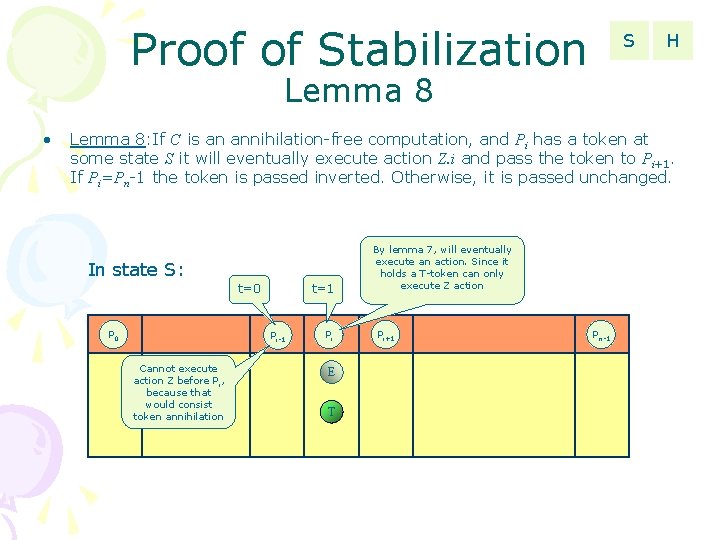
Proof of Stabilization S H Lemma 8 • Lemma 8: If C is an annihilation-free computation, and Pi has a token at some state S it will eventually execute action Z. i and pass the token to Pi+1. If Pi=Pn-1 the token is passed inverted. Otherwise, it is passed unchanged. In state S: t=0 P 0 t=1 Pi-1 Cannot execute action Z before P i, because that would consist token annihilation Pi E T By lemma 7, will eventually execute an action. Since it holds a T-token can only execute Z action Pi+1 Pn-1

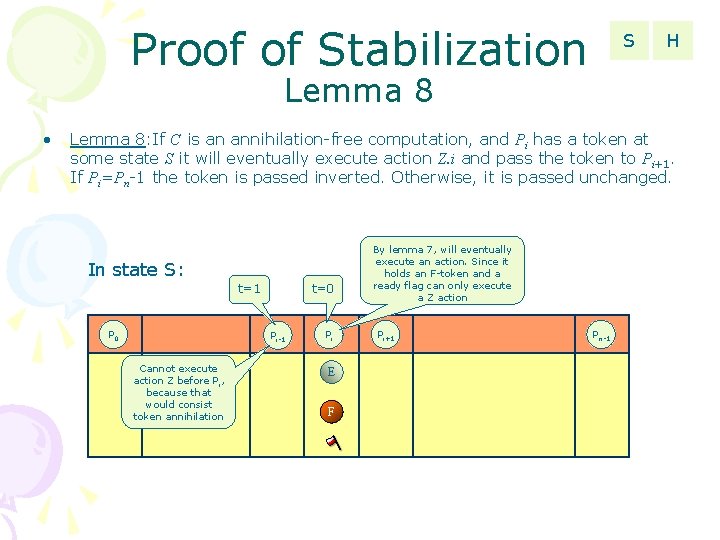
Proof of Stabilization S H Lemma 8 • Lemma 8: If C is an annihilation-free computation, and Pi has a token at some state S it will eventually execute action Z. i and pass the token to Pi+1. If Pi=Pn-1 the token is passed inverted. Otherwise, it is passed unchanged. In state S: t=1 P 0 t=0 Pi-1 Cannot execute action Z before P i, because that would consist token annihilation Pi E F By lemma 7, will eventually execute an action. Since it holds an F-token and a ready flag can only execute a Z action Pi+1 Pn-1

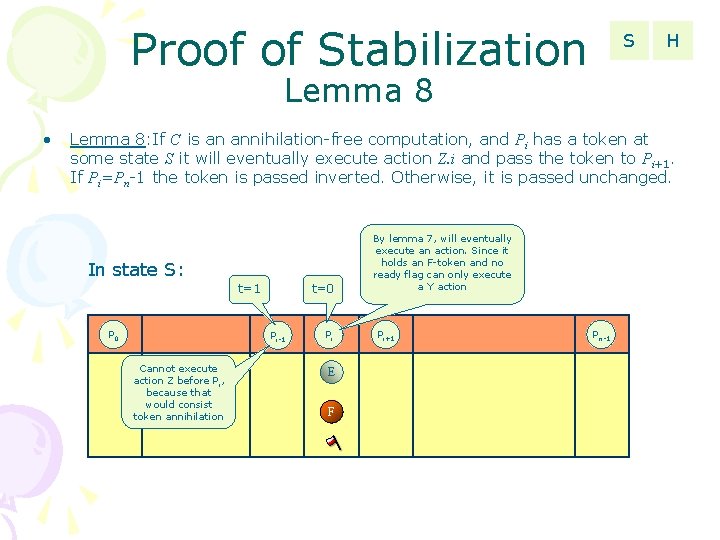
Proof of Stabilization S H Lemma 8 • Lemma 8: If C is an annihilation-free computation, and Pi has a token at some state S it will eventually execute action Z. i and pass the token to Pi+1. If Pi=Pn-1 the token is passed inverted. Otherwise, it is passed unchanged. In state S: t=1 P 0 t=0 Pi-1 Cannot execute action Z before P i, because that would consist token annihilation Pi E F By lemma 7, will eventually execute an action. Since it holds an F-token and no ready flag can only execute a Y action Pi+1 Pn-1

Proof of Stabilization S H Lemma 9 • Lemma 9: In an annihilation-free computation C, if some process Pi has a token at some state, then eventually it passes the token unchanged from one process to the next until it reaches Pn-1. From Pn-1 it is eventually passed inverted to P 0. and the cycle continues. Proof: By continous activation of lemma 8.

Proof of Stabilization S H Lemma 10 • Lemma 10: Every annihilation-free computation C has an infinite suffix C’ such that in every state S in C’, every process Pi has either ready. i=false or ready. i=true and Pi has an F-token Proof: We consider a suffix C’ in which every process has already executed at least one action. We examine state S: If last action was either X or Z then ready=false Can’t execute Z action, after Pi Because C is annihilation-free P 0 Pi-1 Pi If last action was Y then ready=true and had an Ftoken when it exectued it Pn-1

Proof of Stabilization S H Lemma 11 • Lemma 11: Every annihilation-free computation C has an infinite suffix such that the following conditions are satsified: – If an F-token is passed from Pi-1 to Pi in a transition (S, S’) then ready. i=false in S’ – If a T-token is passed inverted from Pn-1 to P 0 in a transition (S, S’), then ready. 0=false in S’ Proof: We examine a suffix C’ as in lemma 10. Let (S, S’) be a transition in C’ in which an F-token is passed from Pi-1 to Pi. Has no token Ftoken (lemma 3) P 0 Pi-1 E F Pi Pi+1 Pn-1 ready=false (lemma 10)

Proof of Stabilization S H Lemma 11 • Lemma 11: Every annihilation-free computation C has an infinite suffix such that the following conditions are satsified: – If an F-token is passed from Pi-1 to Pi in a transition (S, S’) then ready. i=false in S’ – If a T-token is passed inverted from Pn-1 to P 0 in a transition (S, S’), then ready. 0=false in S’ Proof: We examine a suffix C’as in lemma 10. Let (S, S’) be a transition in C’ in which an F-token is passed from Pi-1 to Pi. P 0 Pi-1 Pi E E F T Must execute action or token will be Pi+1 annihilated Pn-1

Proof of Stabilization S H Theorem 1: Every computation C has an infinite suffix in which each state is legal. Proof: Let C be an arbitrary computation of the ring. – By lemma 6, C is infinite. – By lemma 5, The numbers of tokens and enablers in C are non-increasing. – Let C’ be a suffix of C so that in every state there are exactly t tokens, and e enablers. – Let C’’ be a suffix of C’ that satisfies the conditions in lemma 11

Proof of Stabilization Theorem 1 • • S We assume by contradiction that t>1. Let S be the first state of C’’ By lemma 3, there must be a T-token in S By lemma 9, the T-token will be passed unchanged until it reaches Pn-1 and then will be passed inverted to P 0 • By lemma 11, after the T-token is passed to P 0 , ready. 0=false • Let S 0 be the state after the T-token is passed to P 0 • Since a token cannot be passed without an enabler, P 0 has an enabler in S 0 H

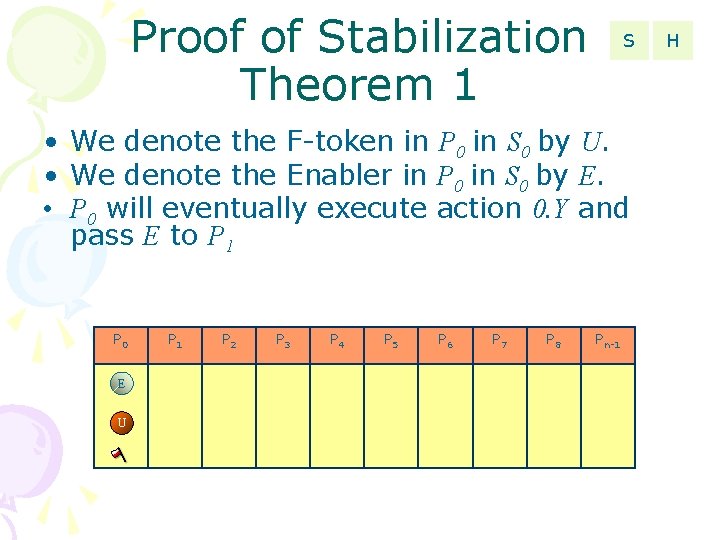
Proof of Stabilization Theorem 1 S • We denote the F-token in P 0 in S 0 by U. • We denote the Enabler in P 0 in S 0 by E. • P 0 will eventually execute action 0. Y and pass E to P 1 P 0 E U P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 Pn-1 H

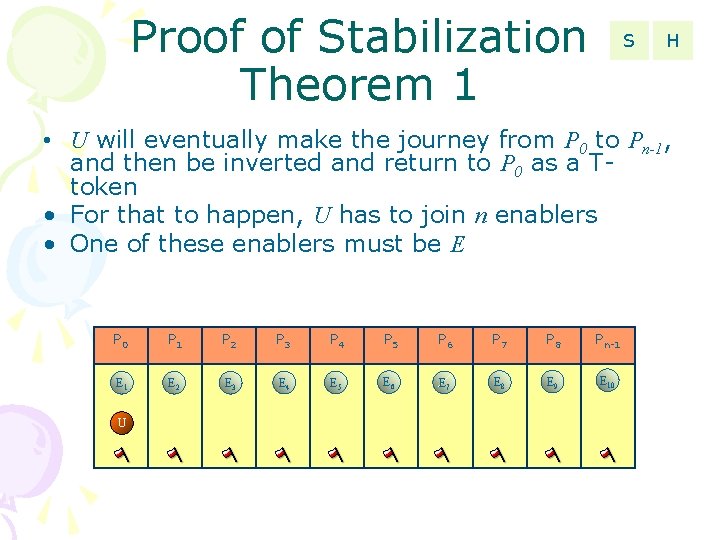
Proof of Stabilization Theorem 1 S H • U will eventually make the journey from P 0 to Pn-1, and then be inverted and return to P 0 as a Ttoken • For that to happen, U has to join n enablers • One of these enablers must be E P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 Pn-1 E 2 E 3 E 4 E 5 E 6 E 7 E 8 E 9 E 10 U

Proof of Stabilization Theorem 1 S • We examine the ring after S 0: H – Since t>1, by lemma 3, there must be a least another Ttoken and another F-token on E’s path. – Let the first T-token after U be V – Let the first F-token after V be W P 0 P 1 P 2 P 3 P 4 P 5 P 6 E U V W P 7 P 8 Pn-1

Proof of Stabilization Theorem 1 S • • H An enabler can’t race past a T-token In order to join U, E must first join V Once E joins V, it will carry V until it is inverted, then drop it at P 0 But then, W will have been inverted too and will stand between E and U • For E to reach U it must join W first. If it does it will carry it all the way to U. • That would cause U and W to be annihilated. Contradiction. • Therefore, t=1. P 0 P 1 P 2 P 3 P 4 P 5 P 6 E V U W V W P 7 P 8 Pn-1

Discussion • What is the time complexity for stabilization ? • Are all the 8 states necessary ? Is it possible to do with less states?