The spin Hall effect The quantum AHE and

The spin Hall effect The quantum AHE and the SHE The persistent spin helix Shou-cheng Zhang, Stanford University Les Houches, June 2006

Credits Collaborators: • Andrei Bernevig (Stanford) • Taylor Hughes (Stanford) • Shuichi Murakami (Tokyo) • Naoto Nagaosa (Tokyo) • Xiaoliang Qi (Tsinghua and Stanford) • Congjun Wu (Stanford and KITP/Santa Barbara) • Yongshi Wu (Utah)

The spin Hall effect

Can Moore’s law keep going? Power dissipation=greatest obstacle for Moore’s law! Modern processor chips consume ~100 W of power of which about 20% is wasted in leakage through the transistor gates. The traditional means of coping with increased power per generation has been to scale down the operating voltage of the chip but voltages are reaching limits due to thermal fluctuation effects.

Spintronics • The electron has both charge and spin. • Electronic logic devices today only used the charge property of the electron. • Energy scale for the charge interaction is high, of the order of e. V, while the energy scale for the spin interaction is low, of the order of 10 -100 me. V. • Spin-based electronic promises a radical alternative, namely the possibility of logic operations with much lower power consumption than equivalent charge based logic operations. • New physical principle but same materials! In contrast to nanotubes and molecular electronics.

Manipulating the spin using the Stern-Gerlach experiment • Problem of using the magnetic field: • hard for miniaturization on a chip. • spin current is even while the magnetic field is odd under time reversal => dissipation just as in Ohm’slaw.

Relativistic Spin-Orbit Coupling • Relativistic effect: a particle in an electric field experiences an internal effective magnetic field in its moving frame • Spin-Orbit coupling is the coupling of spin with the internal effective magnetic field

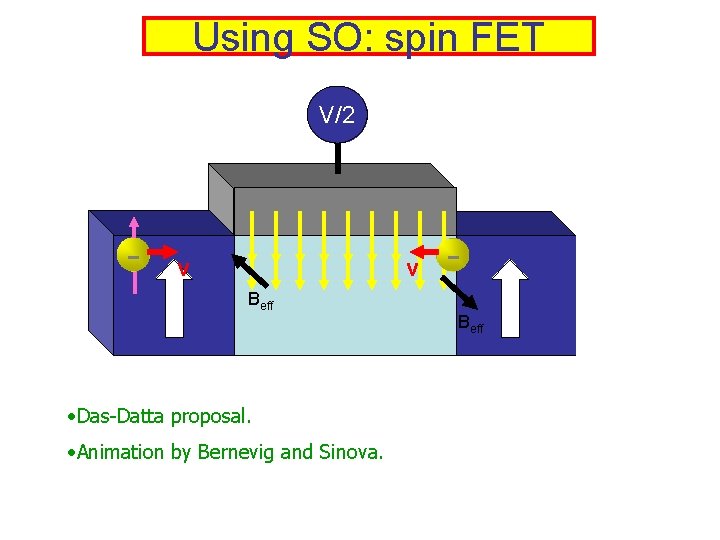
Using SO: spin FET V/2 V - v v Beff • Das-Datta proposal. • Animation by Bernevig and Sinova. Beff

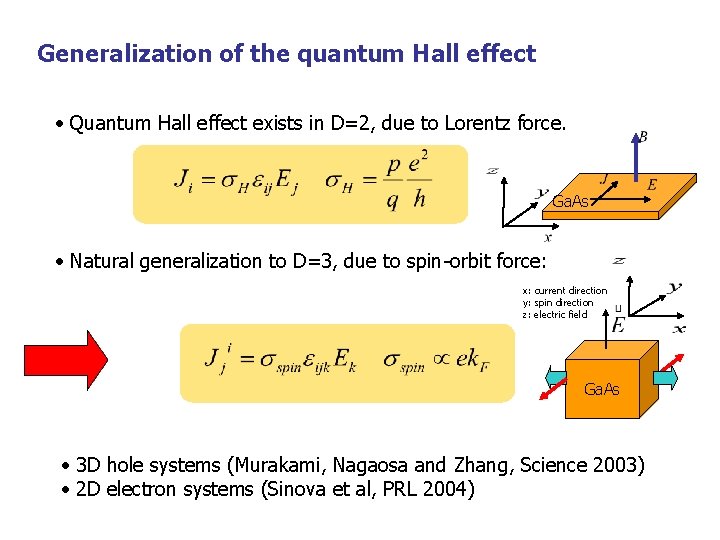
Generalization of the quantum Hall effect • Quantum Hall effect exists in D=2, due to Lorentz force. Ga. As • Natural generalization to D=3, due to spin-orbit force: x: current direction y: spin direction z: electric field Ga. As • 3 D hole systems (Murakami, Nagaosa and Zhang, Science 2003) • 2 D electron systems (Sinova et al, PRL 2004)

Valence band of Ga. As S S P P 3/2 P 1/2 Luttinger Hamiltonian ( : spin-3/2 matrix, describing the P 3/2 band)

Unitary transformation Diagonalize the first term with a local unitary transformation Helicity basis : gauge field in k!

Local gauge field in k space Adiabatic transport = potential V does not cause inter-band transitions only retain the intra-band matrix elements Abelian approximation = retain only the intra-helicity matrix elements

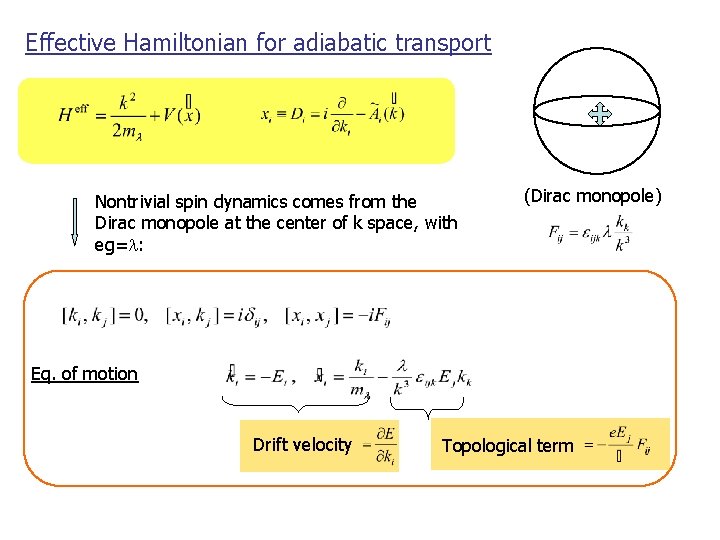
Effective Hamiltonian for adiabatic transport Nontrivial spin dynamics comes from the Dirac monopole at the center of k space, with eg=l: (Dirac monopole) Eq. of motion Drift velocity Topological term

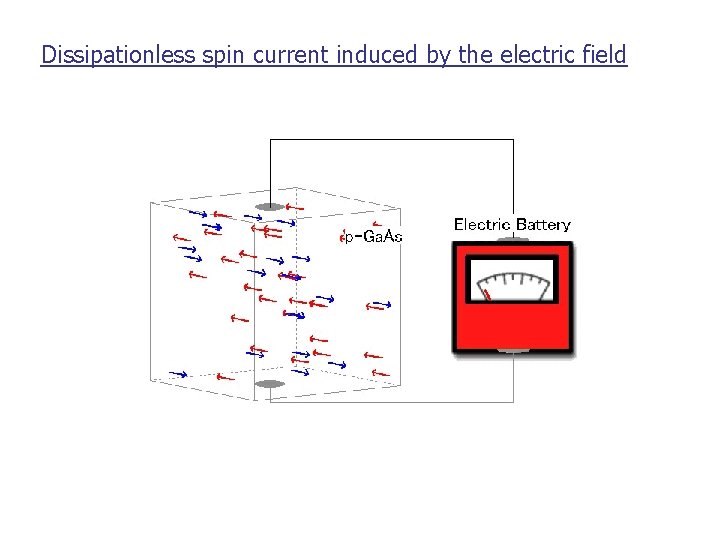
Dissipationless spin current induced by the electric field

The intrinsic spin Hall effect • Key advantage: • electric field manipulation, rather than magnetic field. • dissipationless response, since both spin current and the electric field are even under time reversal. • Topological origin, due to Berry’s phase in momentum space similar to the QHE. • Contrast between the spin current and the Ohm’s law: Energy (e. V) Bulk Ga. As

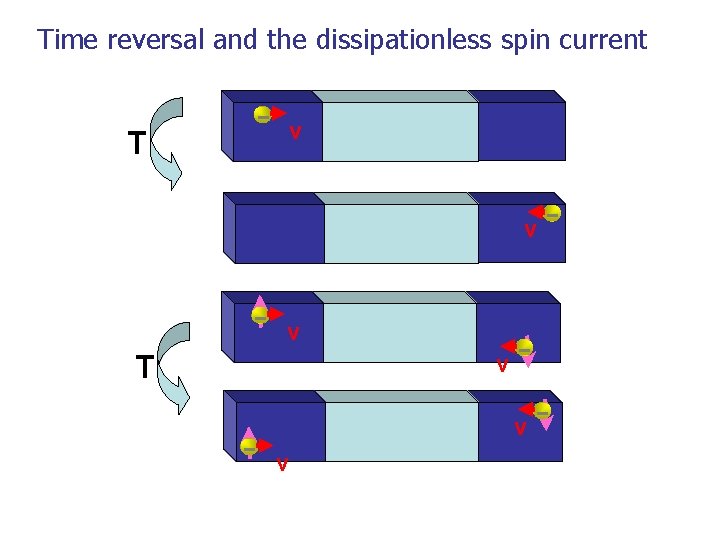
Time reversal and the dissipationless spin current T - v v - v T v - v v - -

Effect due to disorder Luttinger model: + spinless impurities ( -function pot. ) Intrinsic spin Hall conductivity (Murakami et al. (2003)) Vertex correction vanishes identically! 2 DHG Bernevig+Zhang (PRL 2004) Rashba model: + spinless impurities ( -function pot. ) Intrinsic spin Hall conductivity (Sinova et al. (2004)) + Vertex correction in the clean limit (Inoue, Bauer, Molenkamp(2003))

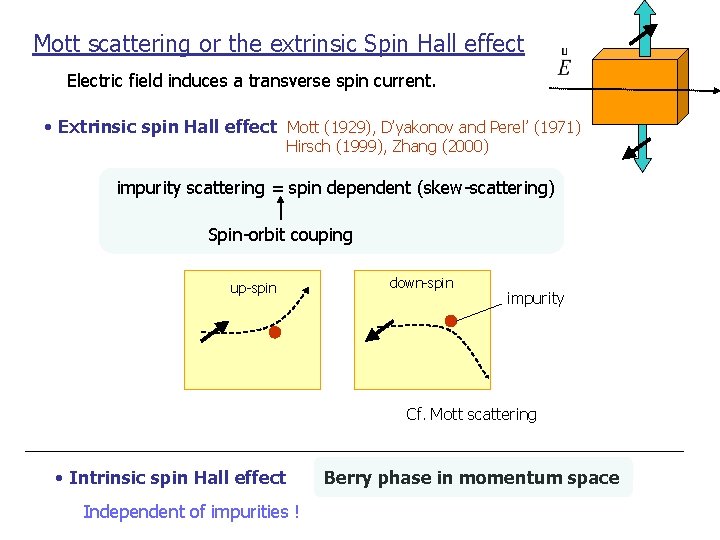
Mott scattering or the extrinsic Spin Hall effect Electric field induces a transverse spin current. • Extrinsic spin Hall effect Mott (1929), D’yakonov and Perel’ (1971) Hirsch (1999), Zhang (2000) impurity scattering = spin dependent (skew-scattering) Spin-orbit couping up-spin down-spin impurity Cf. Mott scattering • Intrinsic spin Hall effect Independent of impurities ! Berry phase in momentum space

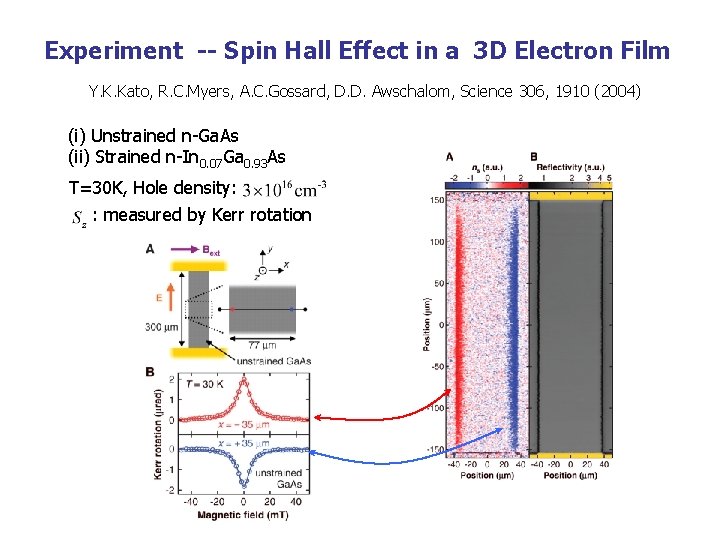
Experiment -- Spin Hall Effect in a 3 D Electron Film Y. K. Kato, R. C. Myers, A. C. Gossard, D. D. Awschalom, Science 306, 1910 (2004) (i) Unstrained n-Ga. As (ii) Strained n-In 0. 07 Ga 0. 93 As T=30 K, Hole density: : measured by Kerr rotation

Experiment -- Spin Hall Effect in a 3 D Electron Film Y. K. Kato et al. , Science (2004) • • unstrained Ga. As -- no strain spin-orbit coupling strained In. Ga. As -- no crystal orientation dependence extrinsic quantum spin hall calculation (Engel, Rashba, Halperin) sign mismatch? but right ballpark value It should be extrinsic! Bernevig, Zhang, cond-mat (2004) • Dresselhaus term is relevant, opposite sign. It could be intrinsic! • Dresselhaus term is small, but induced SHE is not small. • For Dresselhaus term the vertex correction does not cancel the intrinsic SHE. • Dirty limit : SHE suppressed by some factor, which is roughly

Experiment -- Spin Hall Effect in a 2 D Hole Gas J. Wunderlich, B. Kästner, J. Sinova, T. Jungwirth, PRL (2005) • LED geometry • Circular polarization • Clean limit : much smaller than spin splitting • vertex correction =0 (Bernevig, Zhang (2004)) • should be intrinsic

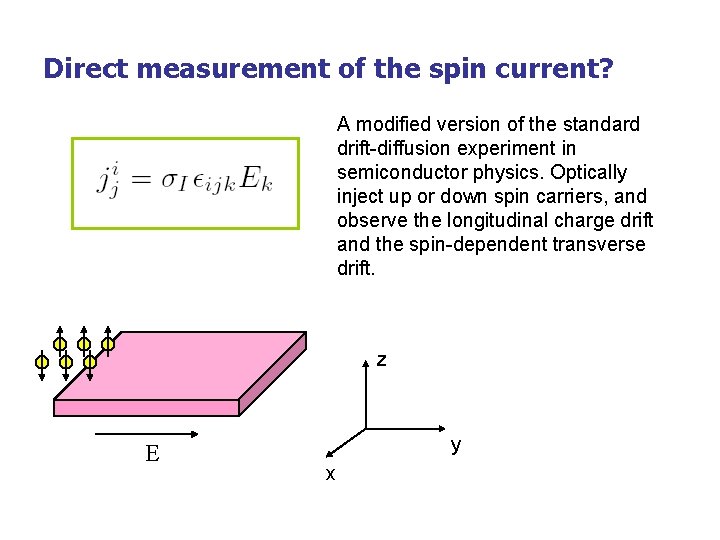
Direct measurement of the spin current? A modified version of the standard drift-diffusion experiment in semiconductor physics. Optically inject up or down spin carriers, and observe the longitudinal charge drift and the spin-dependent transverse drift. z E y x

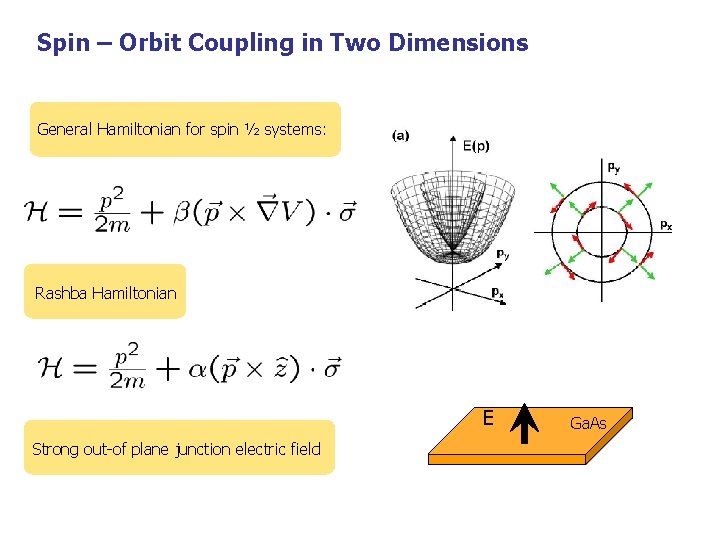
Spin – Orbit Coupling in Two Dimensions General Hamiltonian for spin ½ systems: Rashba Hamiltonian E Strong out-of plane junction electric field Ga. As

Transport In Spin ½ Systems: Two Dimensions • Upon momentum integration continuity equations: • Rashba coupling (2 D Asymmetric Quantum Wells): Burkov Nunez and Mac. Donald; Mishchenko, Shytov and Halperin

Rashba SO Coupling: 2 D Photon Bernevig, Yu and Zhang, PRL 95, 076602 (2005) Spin-Orbit Coupling Maxwell’s Equations

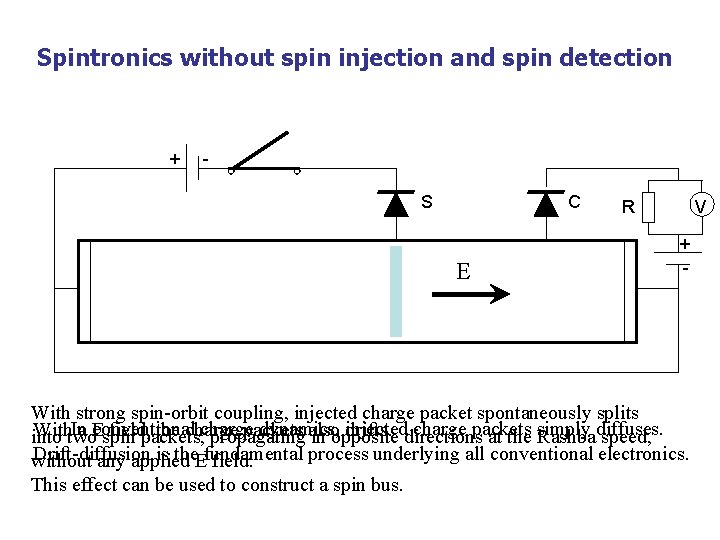
Spintronics without spin injection and spin detection + S C E R V + - With strong spin-orbit coupling, injected charge packet spontaneously splits Ina E conventional charge dynamics, injected charge packets Withtwo field, the charge packets also drifts. directions into spin packets, propagating in opposite at the simply Rashbadiffuses. speed, Drift-diffusion is the. Efundamental process underlying all conventional electronics. without any applied field. This effect can be used to construct a spin bus.

Conclusions • Spin Hall effect is a profoundly deep effect in solid state physics, Natural generalization of the Hall effect and quantum Hall effect. • Natural extensions of the spin Hall effect: orbitronics, spintronics without Spin injection and spin detection, quantum spin Hall effect. • Need close interaction among theory, experiments and materials science. • Frontier of science and technology.