The Spi Calculus A Calculus for Cryptographic Protocols




















- Slides: 21

The Spi Calculus A Calculus for Cryptographic Protocols Presented By Ramesh Yechangunja

Introduction Developed by Martin Abadi and Andrew D. Gordon at the Systems Research Center, it is an extension of the Pi Calculus with cryptographic primitives designed for describing and analyzing cryptographic protocols.

Features • Reliance on the powerful scoping constructs of the pi calculus • Radical definition of the environment as an arbitrary spi calculus process • Representation of security properties, both integrity and secrecy, as equivalences

Basics • Channels may be restricted, so that only certain processes may communicate on them. (Similar to CSP) • The scope of the restriction may change during computation. This is termed scope extrusion. (Different from the earlier process calculi)

• An output process ā‹N›. P is ready to output on channel a. If an interaction occurs, term N is communicated on a and then process P runs. • An input process a(x). P is ready to input from channel a. If an interaction occurs in which N is communicated on a, then process P[N/x] runs.

• A composition P|Q behaves as processes P and Q running in parallel. • A restriction (vn)P is a process that makes a new, private name n, and then behaves as P. • A pair splitting process let (x, y) = M in P behaves as P[N/x][L/y] if term M is the pair (N, L). Otherwise, the process is stuck.

In addition spi calculus introduces primitives for shared-key cryptography • The term {M}N represents the ciphertext obtained by encrypting M under the key N. • The process case L of {x}N in P attempts to decrypt the term L with the key N. If L is a ciphertext of the form {M}N, then the process behaves as P[M/x]. Otherwise, the process is stuck.

A first cryptographic example Consider two principals A and B that share a key KAB with a public channel c. AB. The protocol is simply that A sends a message M under KAB to B, on c. AB. Message 1 A→B: {M}K on c. AB AB In the spi calculus, we write A(M) ≜ c. AB ‹{M}K › AB

- B ≜ c. AB(x). case x of {y}K in F(y) Inst(M) ≜ (v. K)(A(M)|B) AB Security properties are expressed as equivalences. We use the following specification: A(M) ≜ c. AB ‹{M}K › Bspec(M) ≜ c. AB(x). case x of {y}K in F(M) Instspec(M) ≜ (v. KAB)(A(M)|Bspec(M)) AB AB

- We obtain the properties: Authenticity: Inst(M) ≃ Instspec(M), for all M Secrecy: Inst(M) ≃ Inst(M’) if F(M) ≃ F(M’), for all M, M’

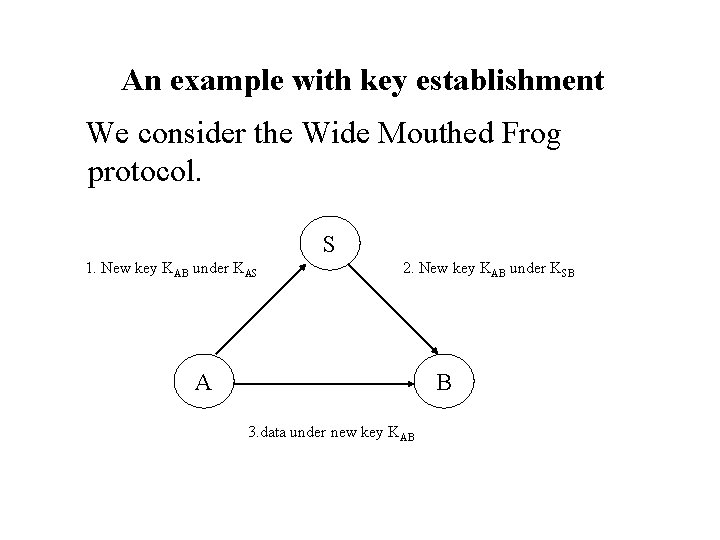
An example with key establishment We consider the Wide Mouthed Frog protocol. S 1. New key KAB under KAS 2. New key KAB under KSB A B 3. data under new key KAB

The protocol is Message 1 A→S: {KAB}K on c. AS Message 2 S→B: {KAB}K on c. SB Message 3 A→B: {M}K on c. AB AS SB AB In the spi calculus, we can express it as: A(M) ≜ (v. KAB)( c. AS ‹{KAB}K ›. c. AB ‹{M}K ›) S ≜ c. AS(x). case x of {y}K in c. SB ‹{y}K › B ≜ c. SB(x). case x of {y}K in c. AB(z). case z of {w}y in F(w) Inst(M) ≜ (v. KAS) (v. KSB)( A(M)|S|B) AS AB AS SB SB

A complete authentication example ( with a flaw) Consider a system with a server and n other principals. Each principal has an input channel which is public, namely, C 1, C 2, …, Cn and Cs. The server shares a pair of keys with each other principal, Ksi and Kis. We extend the previous example to this n+1 principals: Message 1 A→S: A, {B, KAB}K on c. S Message 2 S→B: {A, KAB}K on c. B Message 3 A→B: A, {M}K on c. B AS SB AB

An instance of the protocol is determined by a choice of parties and by the message sent i. e. an instance I is the triple (i, j, M). i – source address j - destination address Given an instance (i, j, M), the following process corresponds to role of A: Send(i, j, M) ≜ (v. K)(c. S ‹(i, {j, K}K )›| cj ‹(i, {M}K)›) i. S The following process corresponds to the role of B: Recv(j) ≜ cj(ycipher). case ycipher of {x. A, xkey}K in cj(z. A, zcipher). [x. A, z. A] case zcipher of {zplain }x in F(x. A, j, zplain) Sj key

The server S is the same- for all instances: S ≜ cj(x. A, xcipher). i 1. . n[x. A is i] case xcipher of {x. B, xkey}K in j 1. . n[x. B is j] cj ‹ {x. A, xkey}K › where i 1. . k Pi is the k-way composition P 1 |…|Pk i. S Sj Finally we define a whole system, parameterized on a list of instances of the protocol: Sys(I 1, …, Im) ≜ (v. Ksi )(v. Kis) (Send(I 1) |…| Send(Im) | !S !Recv(1) |…| !Recv(n) )

- Unfortunately, the protocol is vulnerable to a replay attack that invalidates the authenticity. An attacker can replay messages of one instance and get them mistaken for messages of the other instance.

A complete authentication example (repaired) The previous protocol is improved by adding nonce handshakes as protection against replay attacks. The new protocol is: Message 1 A→S: A on c. S Message 2 S→A: NS on c. A Message 3 A→S: A, {A, A, B, K , NS }K on c. S Message 4 S→B: * on c. B Message 5 B→S: NB on c. S Message 6 S→B: {S, A, B, K , NB }K on c. B Message 7 A→B: A, {M }K on c. B AB AS SB

- In spi calculus, nonces are represented as newly created names. Send(i, j, M) ≜ c. S ‹i›| ci (xnonce). (v. K)(c. S ‹(i, {i, i, j, K, xnonce}K )›| cj ‹(i, {M}K)›) i. S S ≜ c. S(x. A). i 1. . n[x. A is i] (v. NS) (ci ‹NS›| c. S(x’A, xcipher). [x’A is i] case xcipher of {y. A, z. A, x. B, xkey, xnonce}K in j 1. . n[y. A is i][z. A is i][x. B is j][xnonce is NS] (cj ‹*›| c. S (ynonce). cj ‹{S, i, j, xkey, ynonce}K ›)) i. S Sj

- Recv(j) ≜ cj(w). (v. NB) (c. S ‹NB›| cj(ycipher). case ycipher of {x. S, x. A, x. B, xkey, ynonce} K in j 1. . n[x. S is S][x. A is i][x. B is j][ynonce is NB] cj(z. A, zcipher). [ z. A is x. A] case zcipher of {zplain }x in F(i, j, zplain)) Sj key Sys(I 1, …, Im) ≜ (v. Ksi )(v. Kis) (Send(I 1) |…| Send(Im) | !S !Recv(1) |…| !Recv(n) )

- The authenticity property is obtained: Sys(I 1, …, Im) ≃ Sysspec(I 1, …, Im) for any instances I 1, …, Im This holds good because of the nonces. Secrecy: Sys(I 1, …, Im) ≃ Sysspec(J 1, …, Jm) if each pair (I 1, J 1 ), … (Im, Jm) is indistinguishable.

Conclusion • Harder to write protocols but very detailed. • Main advantage is its formal precision • May not be a good tool for finding flaws but yields more convincing proofs of correctness • Protocols prone to attacks are developed without explicit specifications for an attacker. Such precise treatments have not been done before.