The SpaceFilling Efficiency of Urban Form in Izmir

The Space-Filling Efficiency of Urban Form in Izmir: A Historical Perspective Using GIS and Fractal Dimension April 29 th – 30 th, 2011 9 th Meeting of AESOP Thematic Group on “Complexity and Planning” “Self-Organizing and Spatial Planning” Istanbul, TURKEY Gizem Erdoğan, Mc. P Department of City and Regional Planning Pamukkale University Denizli, Turkey K. Mert Cubukcu, Ph. D Department of City and Regional Planning Dokuz Eylul University Izmir, Turkey

Background “Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. ” Mandelbrot (1983)

$Background First introduction of fractals by Mandelbrot (1977) meaning: “irregular and fragmented patterns around$

Background First introduction of fractals by Mandelbrot (1977) meaning: “irregular and fragmented patterns around us, (…) a new geometry of nature”

Background Fractal Dimension (developed by Hausdorff, 1913 and Besicovitch): D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space.

Background Fractals are spatial objects whose geometric characteristics include scale dependence, irregularity, and self-similarity (Shen, 2002)

Background Fractal dimensions of the built-up urban areas is an efficient gateway for describing the urban spatial system and the urban morphology. Spatial fractal theory could be used to analyze the urban physical form and growth processes.

Literature Recent research has demonstrated that the urban form can not be fully described by Euclidean geometry, but rather be treated as fractals (Batty and Longley, 1987; Benguigui and Daoud, 1991; Batty and Xie, 1996; 1999; Shen 1997; 2002). Fractal dimension can avoid disadvantage of scale.

$Literature The fractal dimension is expected to increase as the city becomes increasingly dense,$

Literature The fractal dimension is expected to increase as the city becomes increasingly dense, using the space more efficiently (Ball, 2004).

$Literature The efficiency of urban form can well be measured using fractal dimensions of$

Literature The efficiency of urban form can well be measured using fractal dimensions of the built-up urban areas. Fractal Dimension, D, is not a whole number and it is usually between 1 and 2. 1 2 less efficient space filling more efficient space filling

$Literature Batty and Longley, for example, shows that the fractal dimension of London has$

Literature Batty and Longley, for example, shows that the fractal dimension of London has increased from 1. 32 to 1. 79 between the years 1820 and 1962, indicating a better form of spatial organization and more efficient spacefilling. Lee (1989) analyzed the relationship between urban population and built-up areas in the U. S. in 1960, 1970, and 1980. Çubukçu and Çubukçu (2009), analyzed space-filling efficiency of Safranbolu, Turkey in time series in 1976 and 2007 as 1. 712 and 1. 80 respectively.

Aim To examine the urban space-filling efficiency of a Izmir Metropolitan Area, Turkey, using fractal dimension for five different time periods including 1951, 1963, 1987, 1996 and 2000 using GIS.

Data Izmir is Turkey's third most populous city with 3. 370. 866 (TUİK, 2010) with over 3, 500 years of recorded urban history. and the country's second-largest port city after Istanbul. İzmir has a typical urban growth pattern as an example for Turkey urbanization history where reconstruction was not common until the 1950 s.

Data The data is collected for the İzmir Metropoliten Area for the years 1951, 1963, 1996 and 2000. The data used in the study were derived from the digital and hardcopy aerial photographs and satellite images available from the Municipality of Izmir. Map of 1987 is from Landsat 5 (1, 2, 3), map of 1996 from Landsat 7 (1, 2, 3).

Data is: l scaled l georeferenced l vectorized l Re-rasterized Using Photohop version 6, and then scaled, registered, and vectorized using GIS software, Arc. GIS 9. Calculated using fractal analysis software, Fractalyse.

Data

Analysis Following Batty and Longley (1994) and Shen (1997) and Çubukçu (2009), the box-counting method is applied to estimate fractal dimensions for the five time periods. Box-counting method compute the number of cells cover an object, with grid size and repeat the process changing the box size to obtain a dataset. Regular grid over an object and by counting the number of occupied cells.

$Analysis The estimated fractal dimension D is derived by estimated slope of the log(n(s))$

Analysis The estimated fractal dimension D is derived by estimated slope of the log(n(s)) and log(1/s) graph (Shen, 2002): log(n(s)) = log(U) + Dlog(1/s) + εs D : fractal dimension log(U) : constant (U is builted area) s : the box size εs : the error term

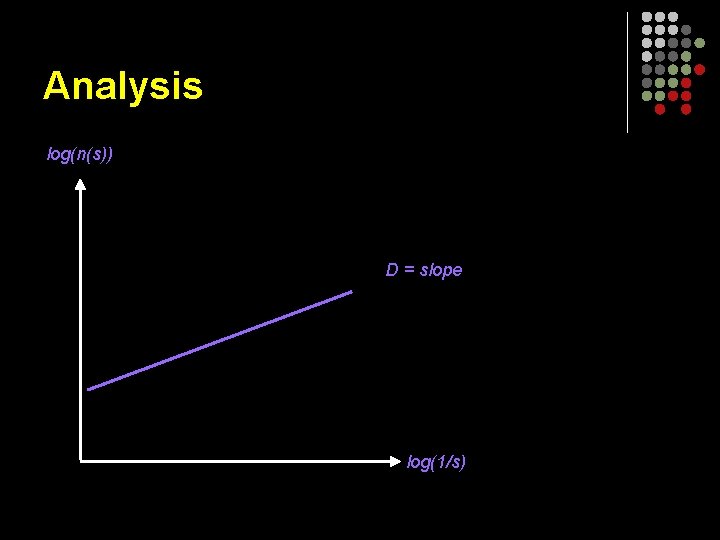
Analysis log(n(s)) D = slope log(1/s)

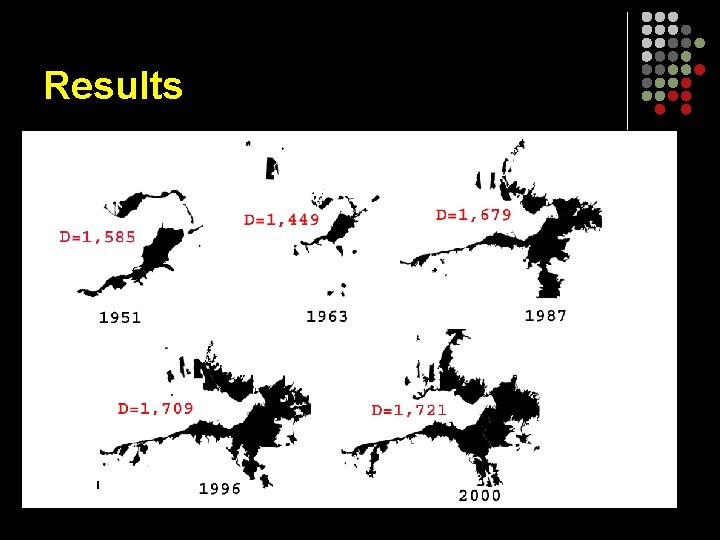
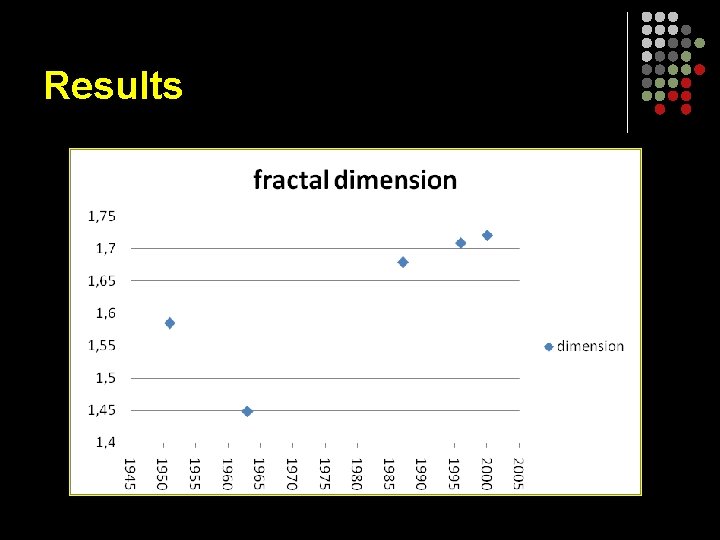
Results

Conclusion The results are parallel to the claims in the literature. The city of İzmir has moved from a less efficient spatial organization and space-filling to a more efficient one between the years 1960 and 2000. The fall from 1, 585 to 1, 449 between 1951 and 1963 can be explained by the first urban spill over as a result of rural to urban migration in the 1950 s.

Caveats l l Data for the years 1951 and 2000 are applied. More time periods (especially 1963 and 1996) should be considered. Methods other than box counting should be applied to generalize resutls.