THE SIMPLEX ALGORITHM Step 1 The objective row

THE SIMPLEX ALGORITHM Step 1 The objective row is scanned and the column containing the most negative term is selected (pivotal column) - indicate with an arrow. Step 2 Divide the value term in each row by the entry in the pivotal column ( -values). The pivot (element) is that which yields the least (non-negative) result. Indicate the pivotal row with an arrow and circle the pivot.

Step 3 Divide the whole pivotal row by the pivot (this leaves the number 1 in place of the pivot) and change the basic variables. Step 4 The aim now is to get zeros everywhere else in the selected column. This is done by adding to each row, multiples of the new pivotal row. The new rows form the next tableau. (You should now have zeros in the pivotal column except for a one where the pivot was) Step 5 Steps 1 to 4 are repeated until the objective row contains no negative elements. At this point, the objective has been attained.

Step 6 To “decode” the information, read down the “basic variable” column, the number in the value column gives the value of that variable. The value of all other variables not present in the final tableau is zero. This is the optimal solution. This will appear meaningless until we illustrate it with an example

Maximise the function Introduce slack variables as follows: 2 x + y + 1 r + 0 s = 32 x +y + 0 r + 1 s = 18 f – 80 x – 70 y + 0 r + 0 s =0 This can be set out in a table as follows:

Step 4 2 Step 3 1 Objective The Divide aim now the value is 70 y to get term zeros in each everywhere row by 32 the else entry in the f 80 x 2 x x + y + 1 r 0 r + + 0 s 0 s 1 s = = 18 0 Divide The theobjective whole pivotal row is row scanned by theand pivot the(this column leaves the function selected pivotal column. ( This -values). is done The by pivot adding (element) to each row, is that number containing 1 in place the ofmost the pivot) negative andterm change is selected the basic multiples which yields of the new least pivotal (non-negative) row. The new result. rows. Indicate form the variables. (pivotal column) - indicate with an arrow. next thetableau. pivotal row with an arrow and circle the pivot. (You insthe pivotal columnθexcept b. v should x nowyhave zeros r Value values for a one where the pivot was) x 12 0. 5 1 0 32 16 32/2 = 16 r s f 01 -80 0 0. 5 1 -30 -70 -0 0. 5 40 0 18 2 1280 0 18/1 R 2 –=R 1 18 Don’t do this for the R 3 + 80 R 1 objective row

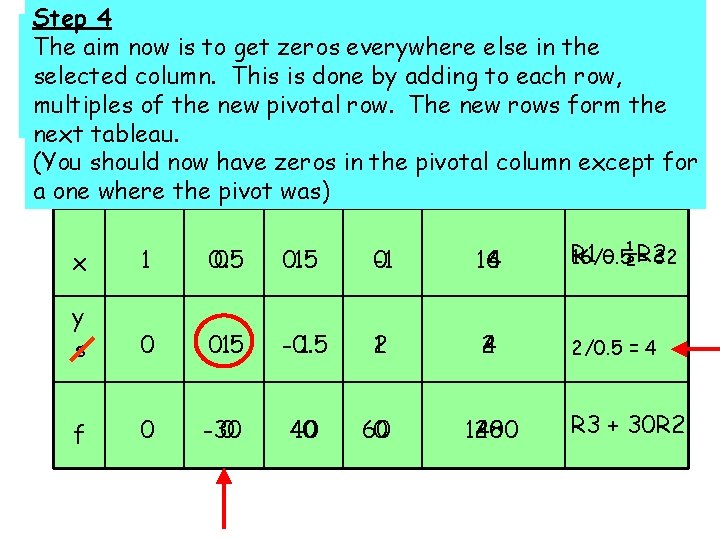
Step 5 2 4 Step 3 Step 1 the following tableau: We now have Steps The Divide aim 1 to now the 4 are isvalue torepeated get term zeros in until each everywhere the rowobjective by the elseentry inrow thein contains the Divide The the whole objective pivotal rowrow is scanned by the pivot and the (this column leaves the no pivotal selected negative column elements. (This -values). is done. The by adding pivot (element) to each row, is that numbercontaining 1 in place the of the most pivot) negative and change term isthe selected basic Atwhich multiples this point, yields of the the new objective least pivotal (non-negative) has row. been Theattained. new result. rows Indicate form the variables. (pivotal column) - indicate with an arrow. next thetableau. pivotal row with an arrow and circle the pivot. (You should now have zeros in the pivotal column except for θ values b. v x y r s Value a one where the pivot was) x 1 0. 5 0 0. 5 1 0 -1 16 14 R 1 - ½R 2 16/0. 5 = 32 y s 0 0. 5 1 --0. 5 1 1 2 2 4 2/0. 5 = 4 f 0 -30 0 40 10 60 0 1280 1400 R 3 + 30 R 2

Step 6 Step 5 To “decode” the information, read down the “basic We now have the following tableau: Steps 1 to 4 are repeated until the objective row contains variable” column, the number in the value column gives the no negative elements. value of that variable. At this point, the objective has been attained. The value of all other variables not present in the final tableau is zero. Also r = s = 0 This is the optimal solution. b. v x y r s Value x 1 0 1 -1 14 x = 14 y 0 1 -1 2 4 y=4 f 0 0 10 60 1400 No f = 1400 negatives