The Simple Linear Regression Model Specification and Estimation

Expenditure by households of a given income on food

Economic Model • Assume that the relationship between income and food expenditure is linear:

Econometric model • Combines the economic model with assumptions about the random nature of

Writing the model with an error term • An observation can be decomposed into

Assumptions of the simple linear regression model

The error term • Unobservable (we never know E(y)) • Captures the effects of

The least squares principle • Fitted regression and predicted values: • Estimated residuals: •

Least Squares Estimates • When data are used with the estimators, we obtain estimates.

Expected value of b 2 Estimator for b 2 can be written: Taking expectations:

Comparing the least squares estimators with other estimators Gauss-Markov Theorem: Under the assumptions SR

The probability distribution of least squares estimators • Random errors are normally distributed: –

Estimating the variance of the error term

Estimating the variances and covariances of the LS estimators

Slides: 19

Download presentation

The Simple Linear Regression Model Specification and Estimation Hill et al Chs 3 and 4

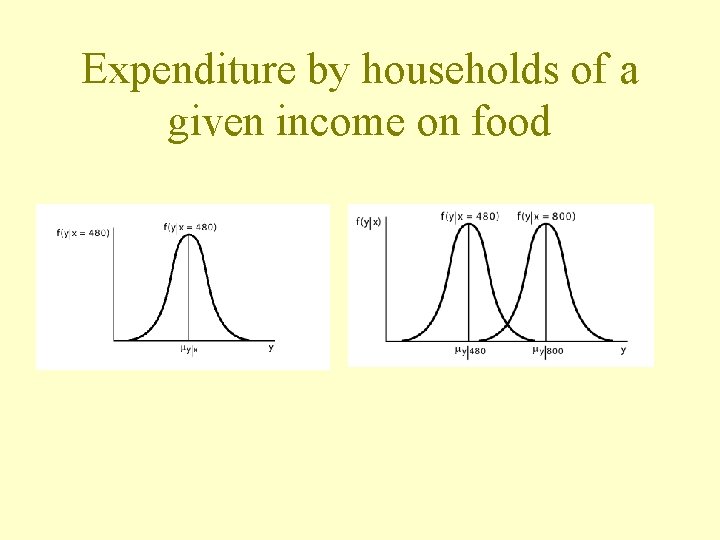
Expenditure by households of a given income on food

Economic Model • Assume that the relationship between income and food expenditure is linear: • But, expenditure is random: • Known as the regression function.

Econometric model

Econometric model • Combines the economic model with assumptions about the random nature of the data. • Dispersion. • Independence of yi and y j. • xi is non-random.

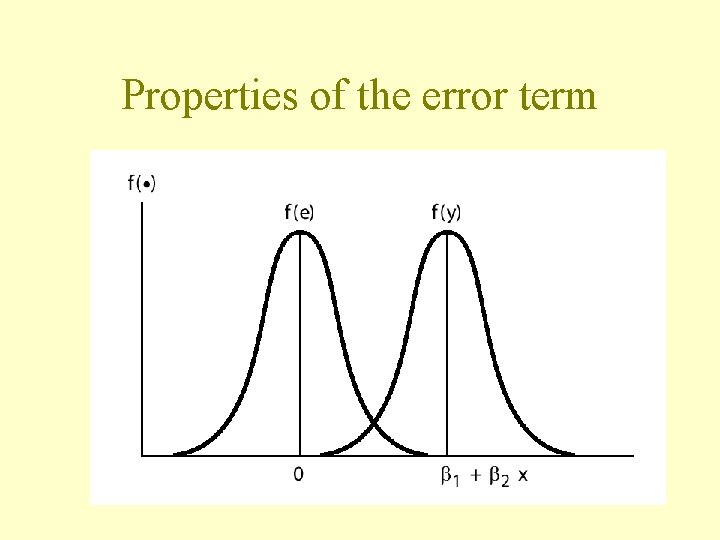
Writing the model with an error term • An observation can be decomposed into a systematic part: – the mean; • and a random part:

Properties of the error term

Assumptions of the simple linear regression model

The error term • Unobservable (we never know E(y)) • Captures the effects of factors other than income on food expenditure: – Unobservered factors. – Approximation error as a consequence of the linear function. – Random behaviour.

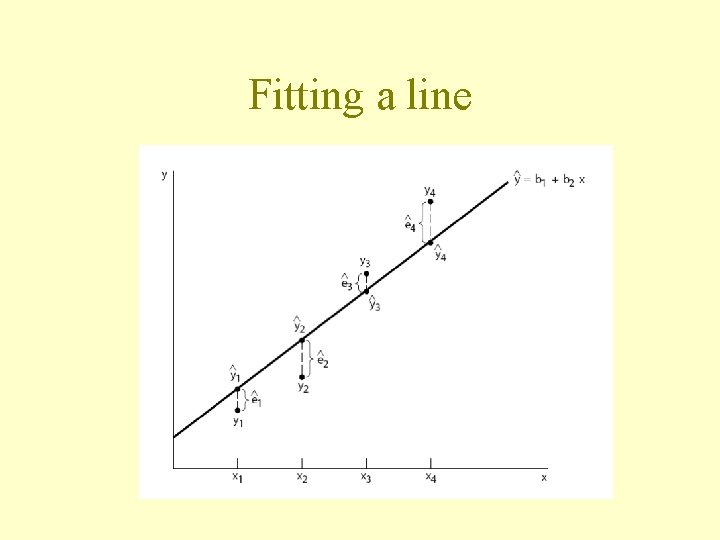
Fitting a line

The least squares principle • Fitted regression and predicted values: • Estimated residuals: • Sum of squared residuals:

The least squares estimators

Least Squares Estimates • When data are used with the estimators, we obtain estimates. • Estimates are a function of the yt which are random. • Estimates are also random, a different sample with give different estimates. • Two questions: – What are the means, variances and distributions of the estimates. – How does the least squares rule compare with other rules.

Expected value of b 2 Estimator for b 2 can be written: Taking expectations:

Variances and covariances

Comparing the least squares estimators with other estimators Gauss-Markov Theorem: Under the assumptions SR 1 -SR 5 of the linear regression model the estimators b 1 and b 2 have the smallest variance of all linear and unbiased estimators of 1 and 2. They are the Best Linear Unbiased Estimators (BLUE) of 1 and 2

The probability distribution of least squares estimators • Random errors are normally distributed: – estimators are a linear function of the errors, hence they a normal too. • Random errors not normal but sample is large: – asymptotic theory shows the estimates are approximately normal.

Estimating the variance of the error term

Estimating the variances and covariances of the LS estimators