The SI System of Measurement le Systme International


































































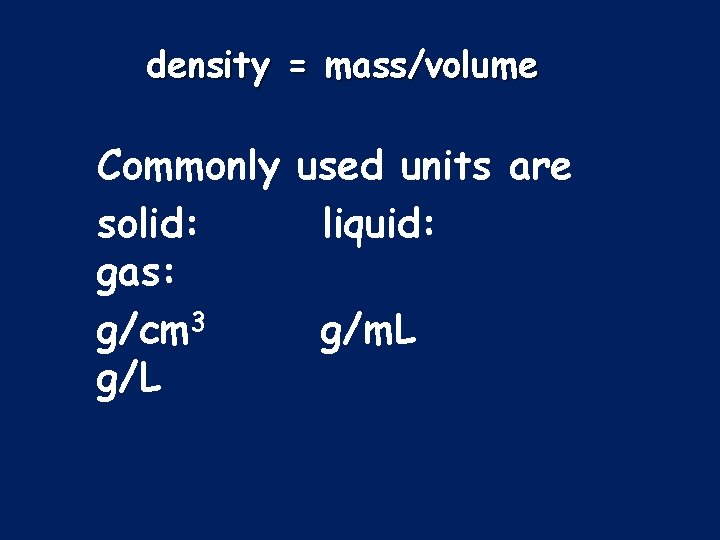







- Slides: 101

The SI System of Measurement (le Système International, SI)

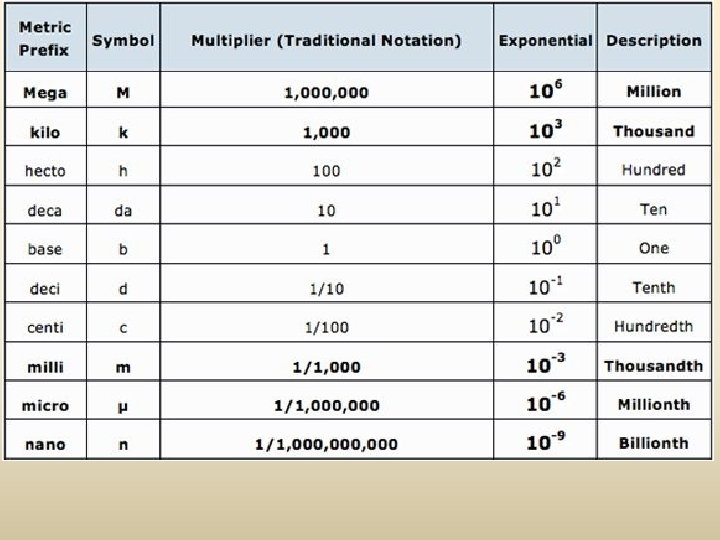
The Fundamental SI Units (le Système International, SI)

The Nature of Measurement A Measurement is a quantitative observation consisting of TWO parts Part 1 - number Part 2 - scale (unit) Examples: 20 grams 73 miles / hour 6. 63 x 10 -34 Joule·seconds

Record this measurement Type your answer in the chat.

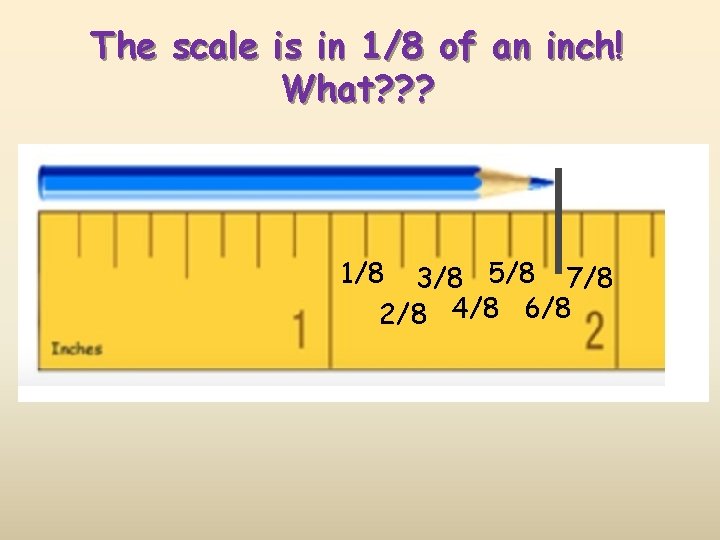
The scale is in 1/8 of an inch! What? ? ? 1/8 3/8 5/8 7/8 2/8 4/8 6/8

Record this measurement Type your answer in the chat.

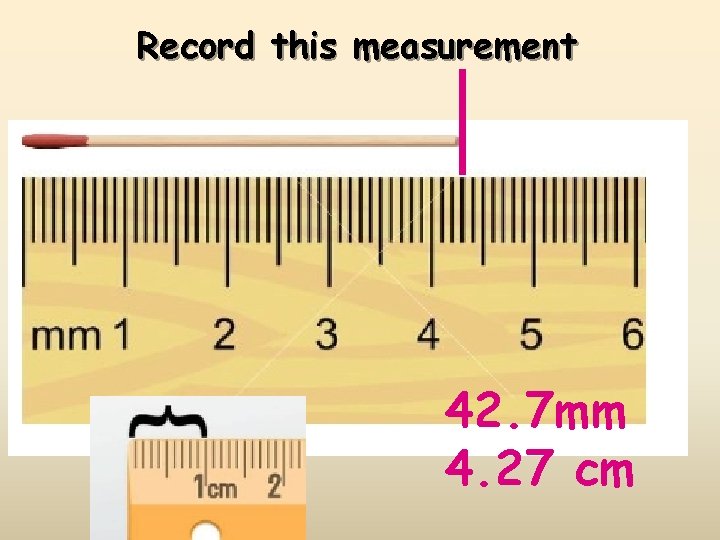
Record this measurement 42. 7 mm 4. 27 cm

Measurements will always have some level of uncertainty. The last digit of a measurement always expresses this uncertainty. When recording a measurement, always express ONE (and only ONE) estimated digit.

Uncertainty and Significant Figures Cartoon courtesy of Lab-initio. com

Uncertainty in Measurement A digit that must be estimated is called uncertain. A measurement always has some degree of uncertainty.

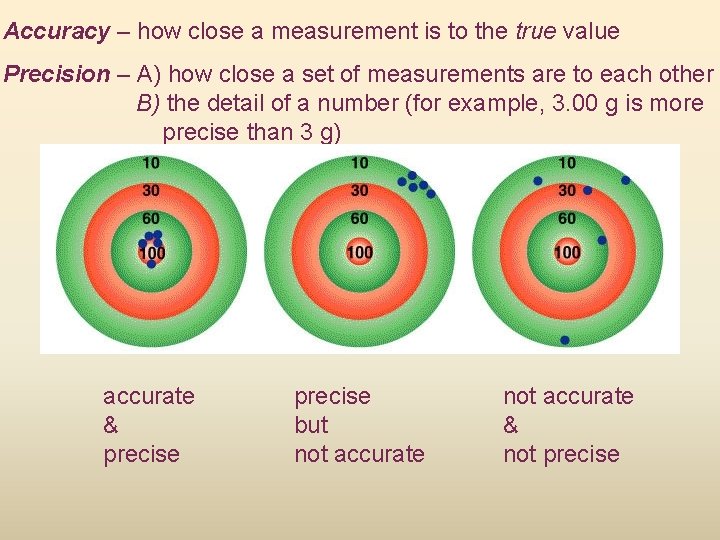
Accuracy – how close a measurement is to the true value Precision – A) how close a set of measurements are to each other B) the detail of a number (for example, 3. 00 g is more precise than 3 g) accurate & precise but not accurate & not precise

Significant Figures ~Fast fingers~

Rules for Counting Significant Figures (Sig. Figs)- Details Nonzero count as integers always significant figures. 3456 has 4 significant figures

Sig. Figs – ZERO Details Leading zeros never count as significant figures. 0. 0486 has 3 significant figures 0. 00000486 has 3 significant figures

Sig. Figs – ZERO Details Captive zeros always count as significant figures. 16. 07 has 4 significant figures

Sig. Figs – ZERO Details Trailing zeros are significant only if the number has a decimal point 9. 300 has 4 significant figures 2500 has 2 significant figures

Sig. Figs Exact numbers & equivalent statements have an infinite number of significant figures. 8 apples 1 inch = 2. 54 cm exactly

Can you summarize the rules for Sig. Figs?

Sig Fig Practice #1 How many significant figures are in each of the following measurements? 24 m. L 2 significant figures 3001 g 4 significant figures 0. 0320 m 3 3 significant figures 6. 4 x 104 molecules 2 significant figures 560 kg 2 significant figures

Sig Fig Practice #2 How many significant figures in each of the following? 1. 0070 m 5 sig figs 17. 10 kg 4 sig figs 100, 890 L 5 sig figs 3. 29 x 103 s 3 sig figs 0. 0054 cm 2 sig figs 3, 200, 000 ns 2 sig figs

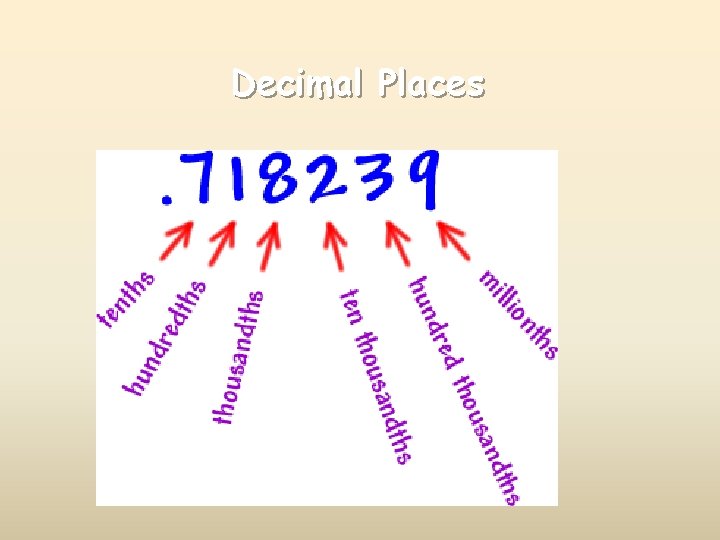
Decimal Places

Significant Figures – Mathematical Operation Rules for Addition or Subtraction The answer cannot have more digits to the right of the decimal point than any of the original numbers. (Answer must match the least precise number in the question. ) 89. 332 +1. 1 90. 432 Shows the thousandths place Only shows the tenth place Answer must match the least precise used, so round off to the tenth place: 90. 4 3. 70 -2. 9133 0. 7867 Shows the hundredth place Shows the ten thousandths place Answer must match the least precise used, so round off to the hundredth place: 0. 79

Significant Figures - Mathematical Operation Rules for Multiplication or Division The number of significant figures in the result is set by the original number that has the smallest number of significant figures. (The answer must match the least # of sigfigs in the question. ) 4. 51 x 3. 6666 = 16. 536366 = 16. 5 3 sig figs round to 5 sig figs 3 sig figs 6. 8 ÷ 112. 04 = 0. 0606926 = 0. 061 round to 2 sig figs 5 sig figs 2 sig figs

Rules for Significant Figures in Mathematical Operations Multiplication and Division: Number of sig figs in the result equals the number in the least precise measurement used in the calculation. 6. 38 x 2. 0 = = 12. 76 rounded to correct # of sigfigs: 13 (2 sig figs)

Sig Fig Practice #3 Calculation Calculator says: Answer 3. 24 m x 7. 0 m 22. 68 m 2 100. 0 g ÷ 23. 7 cm 3 4. 219409283 g/cm 3 4. 22 g/cm 3 23 m 2 0. 02 cm x 2. 371 cm 0. 04742 cm 2 0. 05 cm 2 710 m ÷ 3. 0 s 236. 6666667 m/s 240 m/s 1818. 2 lb x 3. 23 ft 5872. 786 lb·ft 5870 lb·ft 1. 030 g ÷ 2. 87 m. L 2. 9561 g/m. L 2. 96 g/m. L

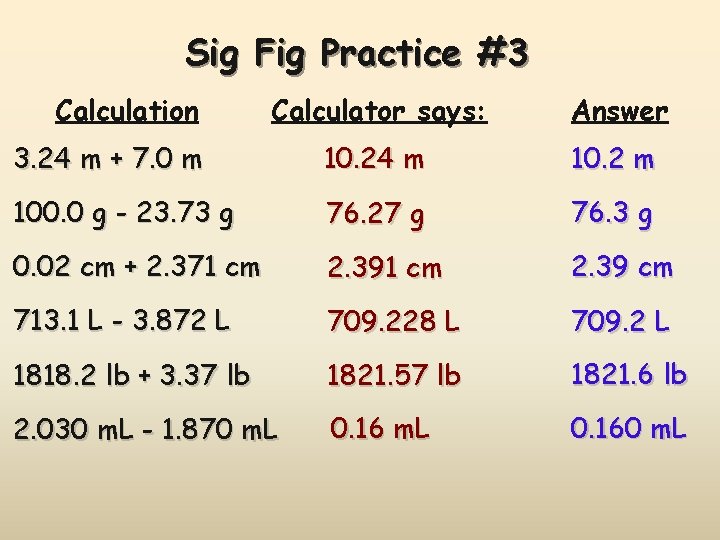
Sig Fig Practice #3 Calculation Calculator says: Answer 3. 24 m + 7. 0 m 10. 24 m 10. 2 m 100. 0 g - 23. 73 g 76. 27 g 76. 3 g 0. 02 cm + 2. 371 cm 2. 39 cm 713. 1 L - 3. 872 L 709. 228 L 709. 2 L 1818. 2 lb + 3. 37 lb 1821. 57 lb 1821. 6 lb 2. 030 m. L - 1. 870 m. L 0. 160 m. L

Significant Figures Exact Numbers from definitions or numbers of objects are considered to have an infinite number of significant figures. (They will not Limit the number of sigfigs in our answer. ) The average of 3 measured lengths (in m); 6. 64, 6. 68 and 6. 70? 6. 64 + 6. 68 + 6. 70 = 20. 02 3 3 = 6. 67333 = 6. 673 cm = 7 cm Because 3 is an exact number. We knew there were exactly 3 measurements. That 3 supplies an infinite amount of sigfigs.

SCIENTIFIC NOTATION

Scientific Notation In science, we deal with some very LARGE numbers: 1 mole = 60220000000000 atoms In science, we deal with some very SMALL numbers: Mass of an electron = 0. 000000000000000091 kg

Imagine the difficulty of calculating the mass of 1 mole of electrons! 0. 000000000000000091 kg x 60220000000000 atoms ? ? ? ? ? ? ? ? ?

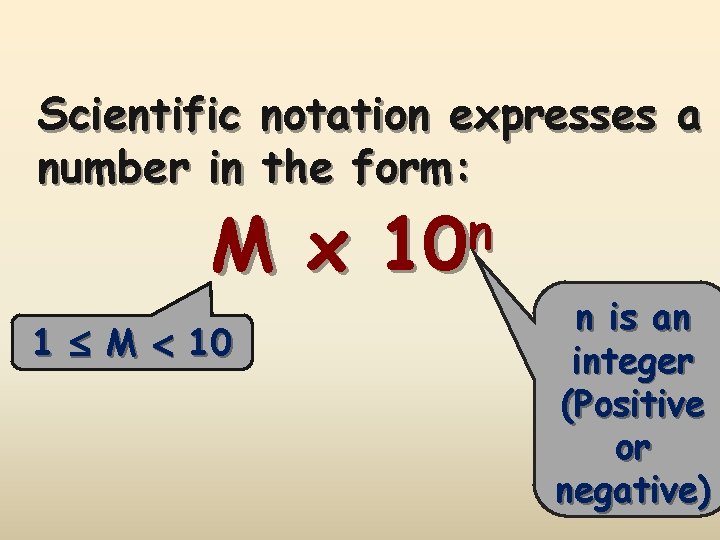
Scientific Notation: A method of representing very large or very small numbers in the form: n M x 10 1 M 10 Examples for M Correct: 7 Correct: 1. 2 Correct: 5. 003 Not correct: 0. 9 Not correct: 12. 1 Examples for n Correct: 2 ni sa Correct: -3 i nte n Correct: 6 (ca ger Not correct: p 2. 5 n o b s itiv e Not correct: -0. 003 neg ve ati or ve)

How to convert a regular # to scientific notation . 2 500 000 9 8 7 6 5 4 3 2 1 Step #1: Insert an understood decimal point for the regular number Step #2: Decide where the decimal must end up so that M will be in the correct format Step #3: Count how many places you bounce the decimal point so that M will be in the correct format Step #4: Re-write in the form M x 10 n

2 500 000 2. 5 x 9 10 The exponent is positive because the decimal form of the number we started with was greater than 1.

0. 0000579 1 2 3 4 5 Step #1: Insert an understood decimal point Step #2: Decide where the decimal must end up so that M will be in the correct format Step #3: Count how many places you bounce the decimal point so that M will be in the correct format Step #4: Re-write in the form M x 10 n

0. 0000579 5. 79 x -5 10 The exponent is negative because the decimal form of the number we started with was less than 1.

Right? Left? +? -? 2. 5 x 6 10

Right? Left? +? -? 2 x -3 10

Right? Left? +? -? Don’t worry about lefts and rights. • If the number value is big, the exponent will be positive. • If the number value is small, the exponent will be negative.

Scientific notation expresses a number in the form: M x 1 M 10 n is an integer (Positive or negative)

Practice Questions Rewrite the number in scientific notation 45000 4 4. 5 x 10

Practice Questions Rewrite the number in scientific notation 7, 560, 000 (those are commas) 6 7. 56 x 10

Practice Questions Rewrite the number in scientific notation 0. 000003277 -6 3. 277 x 10

Practice Questions Rewrite the number in scientific notation 0. 621 -1 6. 21 x 10

Practice Questions Rewrite the number in scientific notation 8920 3 8. 92 x 10 ALL sigfigs must be rewritten in the scientific notation.

Practice Questions Rewrite the number in scientific notation 1455. 0 3 1. 4550 x 10 ALL sigfigs must be rewritten in the scientific notation.

Stretch Break!

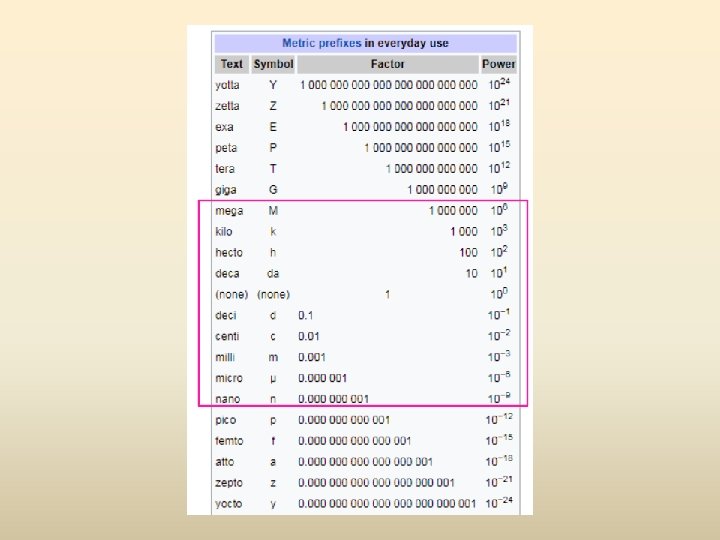
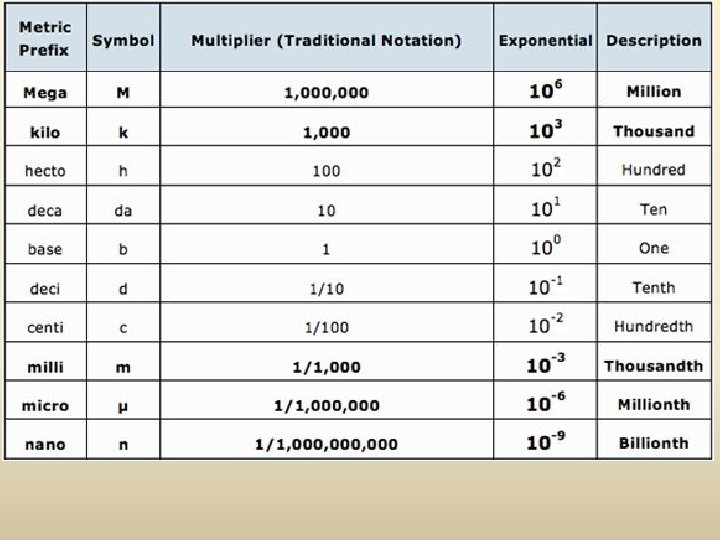
Metric System Prefixes



M K H D U D C M mn King Henry Died Unexpectedly Drinking Chocolate Milk

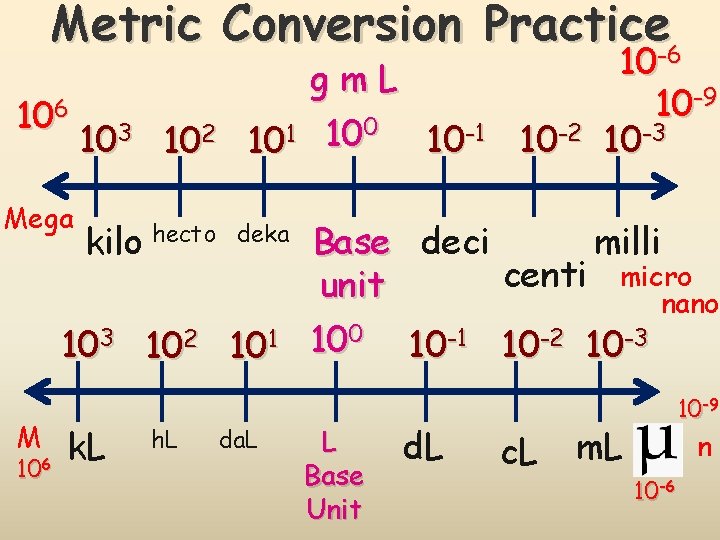
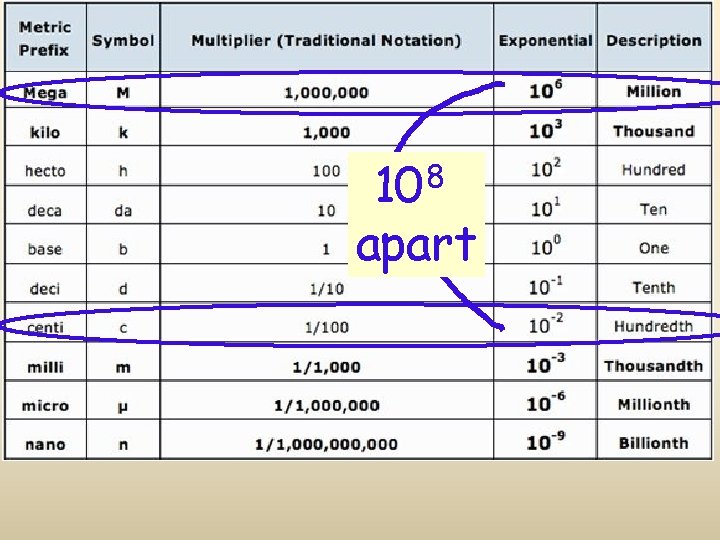
Metric Conversions 103 102 101 g m L kilo hecto deka Base k h da unit 10 -1 10 -2 10 -3 deci centi milli d c m Conversions in the metric system are merely a matter of moving a decimal point. The “base unit” means the you have a quantity (grams, meters, Liters, etc without a prefix.

Metric Conversion Practice-6 106 Mega 103 102 kilo hecto gm. L 0 1 10 10 -1 10 -2 10 deka 103 102 101 M 106 k. L h. L da. L 10 10 -9 10 -3 Base deci milli centi micro unit nano 100 10 -1 10 -2 10 -3 L Base Unit d. L c. L 10 -9 m. L n 10 -6

Metric Conversions 103 102 101 g m L 10 -1 10 -2 10 -3 kilo hecto deka Base deci centi milli unit 1 2 3 18. L 18. liters = 18, 000. m. L Example #1: Convert 18 liters to milliliters 18 liters = 18000 m. L Stay consistent with sigfigs. You must rewrite the same number of sigfigs.

Metric Conversions 103 102 101 g m L kilo hecto deka Base unit 450. mg = 0. 450 g 10 -1 10 -2 10 -3 deci centi milli 3 2 1 450. mg Example #2: Convert 450 milligrams to grams 450 mg = 0. 45 g Stay consistent with sigfigs. You must rewrite the same number of sigfigs.

Metric Conversions 103 102 101 g m L 10 -1 10 -2 10 -3 kilo hecto deka Base deci centi milli unit 2 3 1 4 5 6 20 kg = 20, 000 mg Example #3: Convert 20 kilograms to milligrams


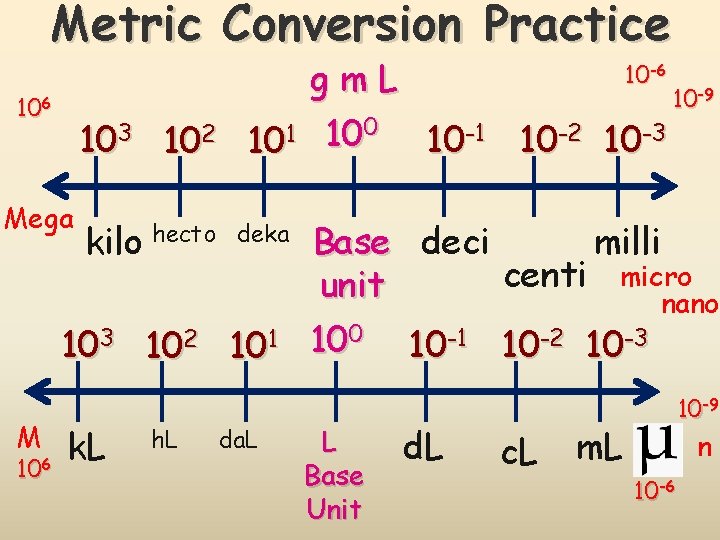
Metric Conversion Practice gm. L 10 -9 0 1 10 10 -1 10 -2 10 -3 10 10 -6 103 102 Mega kilo hecto deka 103 102 101 M 106 k. L h. L da. L Base deci milli centi micro unit nano 100 10 -1 10 -2 10 -3 L Base Unit d. L c. L 10 -9 m. L n 10 -6

micro symbol (a lowercase Mu)

Dimensional Analysis Method of Metric Conversion How many m. L are in 1. 632 L? 1. Determine which unit conversion factor(s) are needed • Always relate the smaller unit to 1 of the larger unit • As in m. L vs. L, 1000 m. L are in 1 L 2. Carry units through calculation 3. If all units cancel except for the desired unit(s), then the problem was set up correctly. 4. Round to proper number of sigfigs. 1 L = 1000 m. L (this statement has infinite sigfigs!) 1000 m. L 1. 632 L x = 1632 m. L 1 L 2 1 L L 1. 632 L x = 0. 001632 1000 m. L

Equivalent Units Practice cm vs. mm • Always relate the smaller unit to 1 of the larger unit • cm is the larger unit, mm is the smaller unit • Equivalent statement would be 1 cm = 10 mm (they are 103 102 101 100 1 10 away) 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

Equivalent Units Practice mm vs. hm • Always relate the smaller unit to 1 of the larger unit • hm is the larger unit, mm is the smaller unit • Equivalent statement would be 1 hm = 100000 mm (they are 105 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

Equivalent Units Practice km vs. mm • Always relate the smaller unit to 1 of the larger unit • km is the larger unit, mm is the smaller unit • Equivalent statement would be 1 km = 1000000 mm (they are 106 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

L vs. d. L Equivalent Units Practice • Always relate the smaller unit to 1 of the larger unit • L is the larger unit, d. L is the smaller unit • Equivalent statement would be 1 L = 10 d. L (they are 101 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

cg vs. kg Equivalent Units Practice • Always relate the smaller unit to 1 of the larger unit • kg is the larger unit, cg is the smaller unit • Equivalent statement would be 1 kg = 100000 cg (they are 105 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

Got it? ?

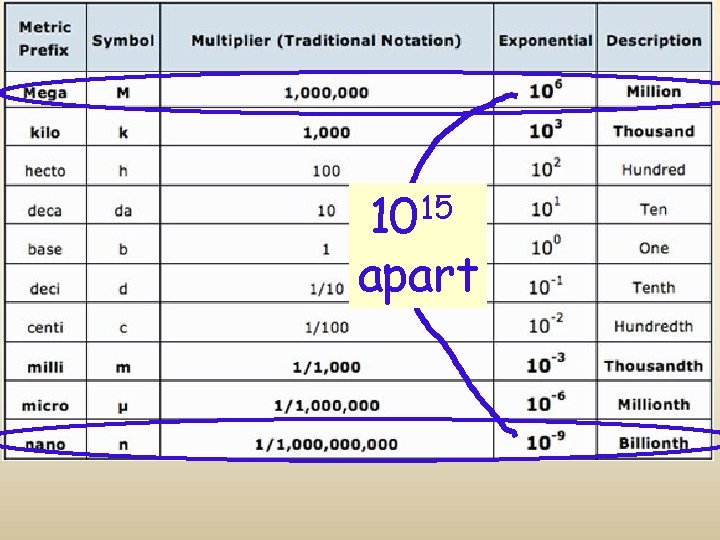
Equivalent Units Practice Mg vs. ng • Always relate the smaller unit to 1 of the larger unit • Mg is the larger unit, ng is the smaller unit • Equivalent statement would be • Type your answer in the chat! 1 Mg = 100000000 ng (they are 1015 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

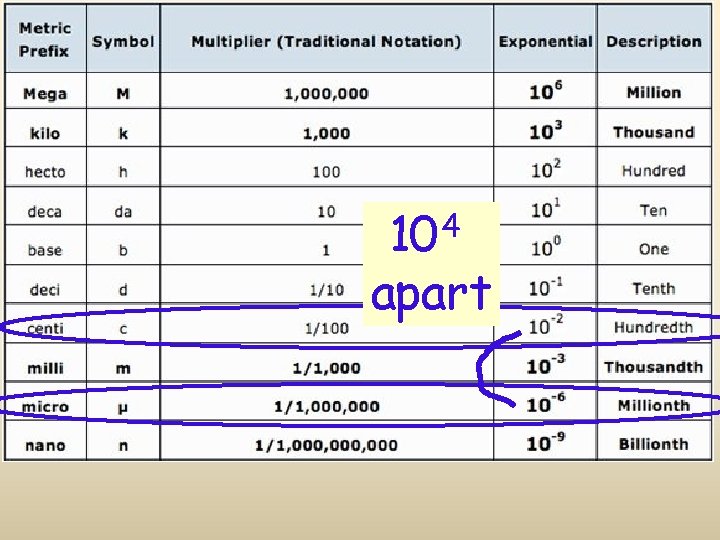
15 10 apart

NOW… You got it? ?

Equivalent Units Practice Ѽg vs. �g • Always relate the smaller unit to 1 of the larger unit 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

Equivalent Units Practice µm vs. cm • Always relate the smaller unit to 1 of the larger unit • Type your answer in the chat! • cm is the larger unit, µm is the smaller unit • Equivalent statement would be 1 cm = 10000 µm (they are 104 away) 103 102 101 100 10 -1 10 -2 10 -3 hecto kilo deka deci centi milli Base

104 apart

Dimensional Analysis Method of Solving Problems 1. Determine which unit conversion factor(s) are needed • Always relate the smaller unit to 1 of the larger unit 2. Carry units through calculation 3. If all units cancel except for the desired unit(s), then the problem was set up correctly. 4. Round to proper number of sigfigs. How many g are in 355 kg? 1 kg = 1000 g (this equivalent statement has infinite sigfigs!) 1000 g 355 kg x 1 kg = 355000 g

The speed of sound in air is about 343 m/s. What is this speed in miles per hour? meters to miles seconds to hours 1 mi = 1609 m EXACTLY 1 min = 60 s EXACTLY 343 m x 1 mi x 60 s s 1609 m 1 min 1 hour = 60 min EXACTLY 60 min mi x = 767 hour 1. Determine which unit conversion factor(s) are needed 2. Carry units through calculation 3. If all units cancel except for the desired unit(s), then the problem was solved correctly. 4. Round to proper number of sigfigs.

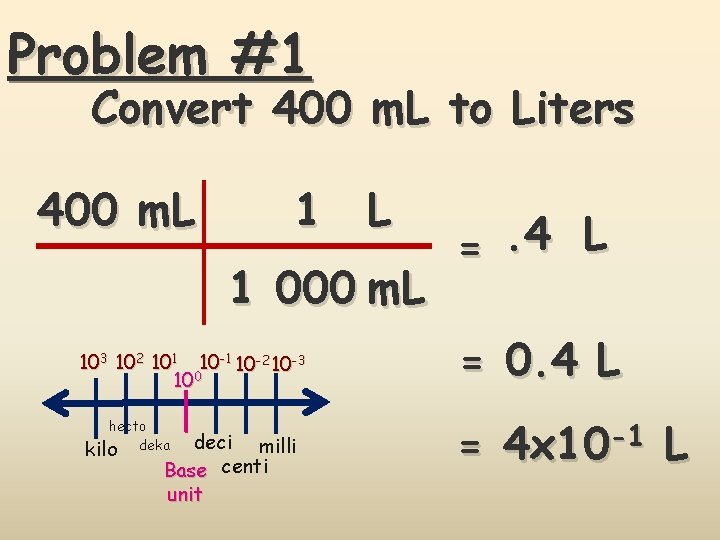
Problem #1 Convert 400 m. L to Liters 400 m. L 1 000 m. L 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit =. 4 L = 0. 4 L = 4 x 10 -1 L

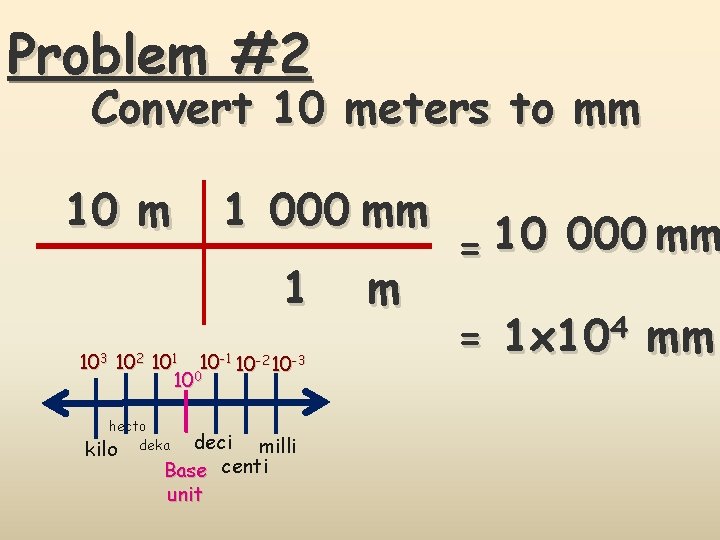
Problem #2 Convert 10 meters to mm 10 m 1 000 mm 1 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit m = 10 000 mm = 1 x 104 mm

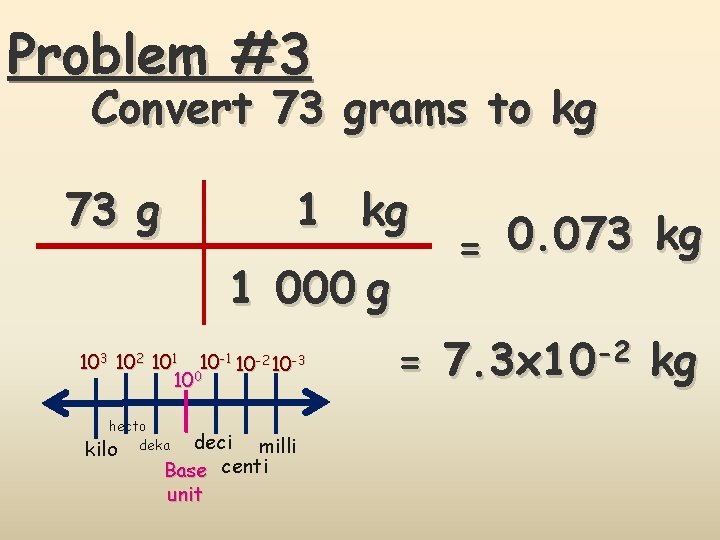
Problem #3 Convert 73 grams to kg 1 kg 73 g 1 000 g 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 0. 073 kg = 7. 3 x 10 -2 kg

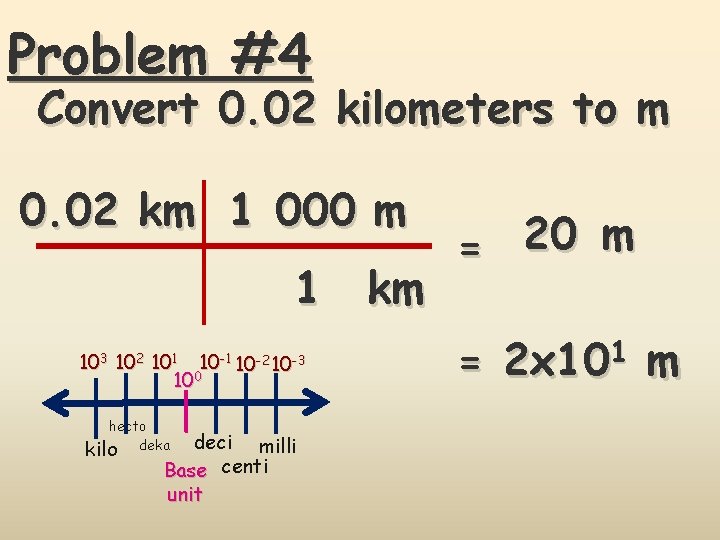
Problem #4 Convert 0. 02 kilometers to m 0. 02 km 1 000 m 1 km 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 20 m = 2 x 101 m

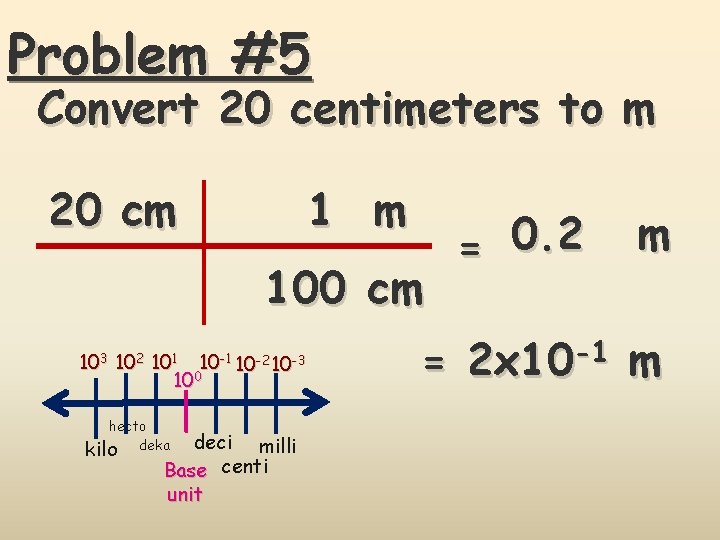
Problem #5 Convert 20 centimeters to m 1 m 20 cm 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 0. 2 m = 2 x 10 -1 m

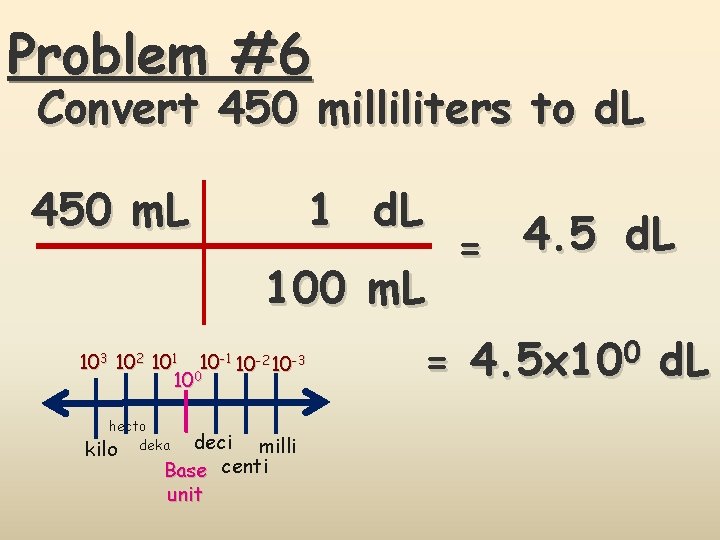
Problem #6 Convert 450 milliliters to d. L 1 d. L 450 m. L 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 4. 5 d. L = 4. 5 x 100 d. L

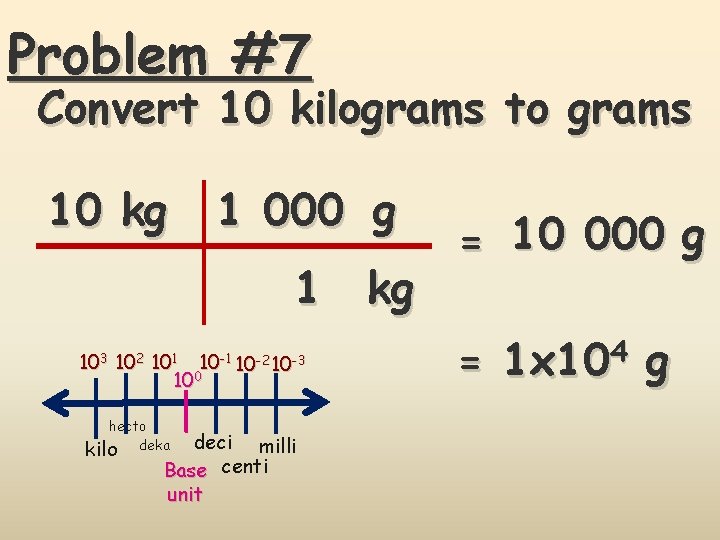
Problem #7 Convert 10 kilograms to grams 10 kg 1 000 g 1 kg 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 10 000 g = 1 x 104 g

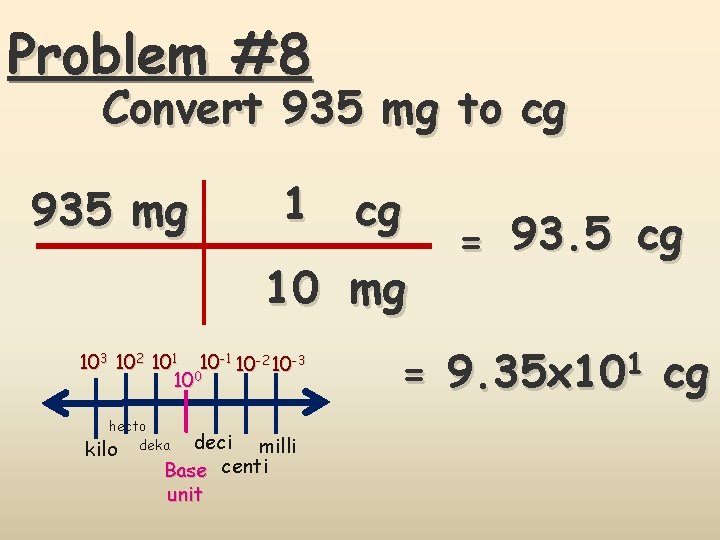
Problem #8 Convert 935 mg to cg 935 mg 1 cg 10 mg 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 93. 5 cg = 9. 35 x 101 cg

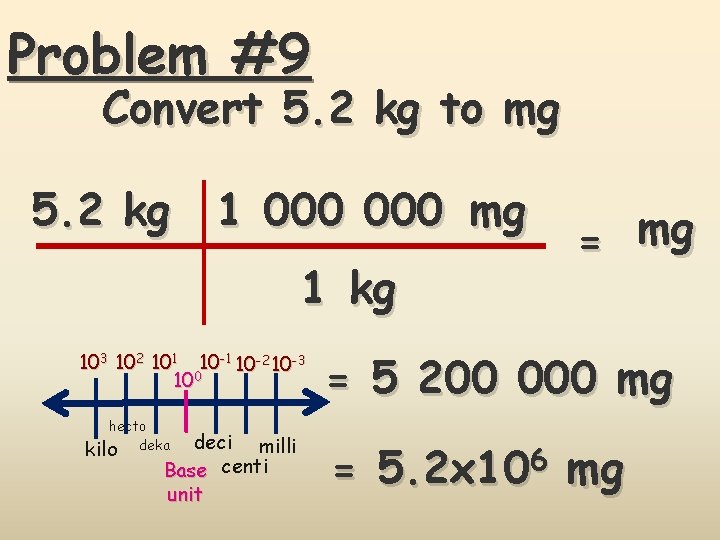
Problem #9 Convert 5. 2 kg to mg 5. 2 kg 1 000 mg 1 kg 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = mg = 5 200 000 mg = 5. 2 x 106 mg

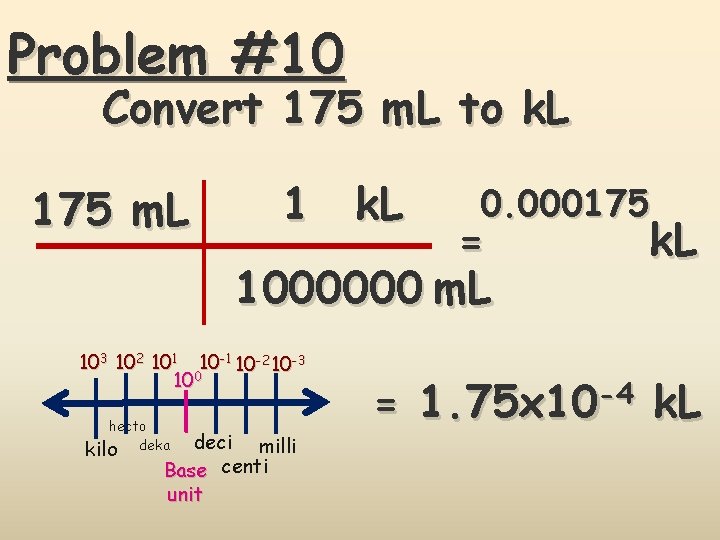
Problem #10 Convert 175 m. L to k. L 175 m. L 1 k. L = 1000000 m. L 103 102 101 10 -2 10 -3 100 hecto kilo deka 0. 000175 deci milli Base centi unit k. L = 1. 75 x 10 -4 k. L

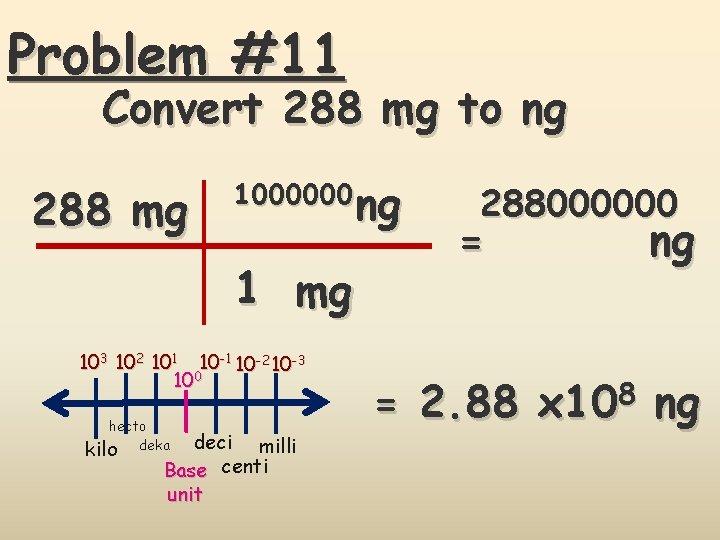
Problem #11 Convert 288 mg to ng 288 mg 1000000 ng ng 1 mg 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit 288000000 = ng = 2. 88 x 108 ng

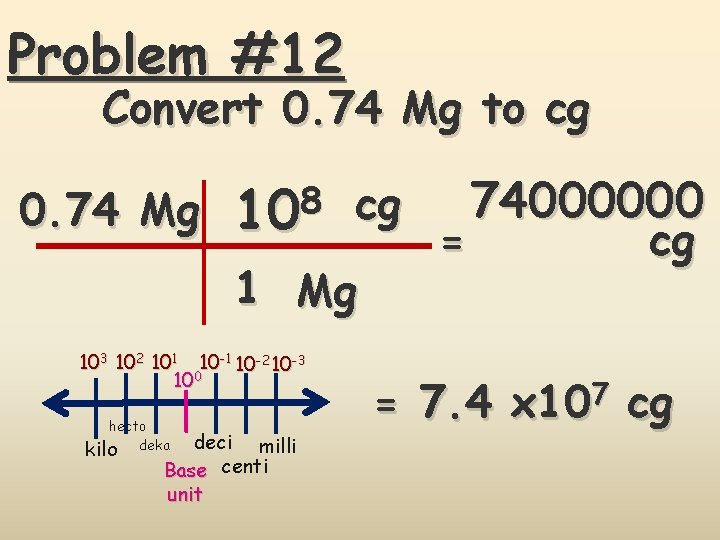
Problem #12 Convert 0. 74 Mg to cg 0. 74 Mg 8 10 cg 1 Mg 103 102 101 10 -2 10 -3 100 hecto kilo deka deci milli Base centi unit = 74000000 cg = 7. 4 x 107 cg

8 10 apart

Derived SI units derived unit a unit that can be obtained from combinations of fundamental units.


Where do urban bears live? Hint: mass over volume

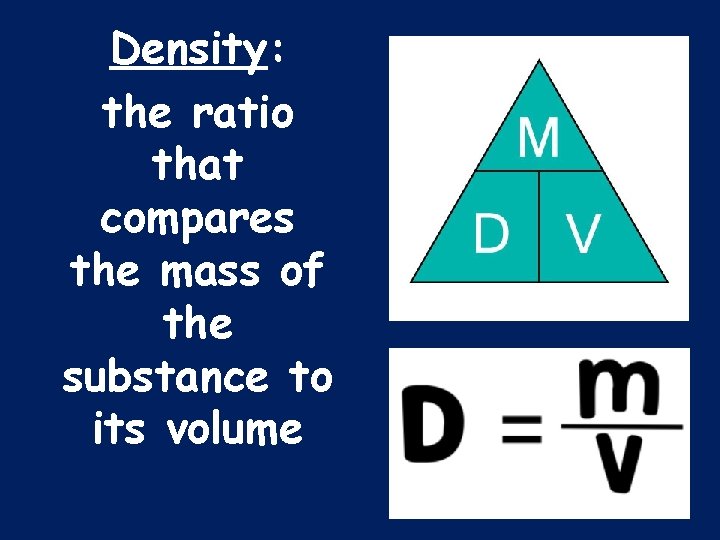
Density: the ratio that compares the mass of the substance to its volume

Draw a picture of a cube that is 1 cm x 1 cm below: 1 cm What is the volume of this box? Volume = lwh Volume = (1 cm) 1 cm (1 cm) Volume = 1 cm 3 If you fill the box with water, what is the volume of the water?

Milliliter (m. L): 1 m. L = 1 cm 3 = 1 cc What does cc mean? cubic centimeter

Important fact to memorize is 1 m. L of pure water = 1 g The density of pure water is 1. 00 g/m. L
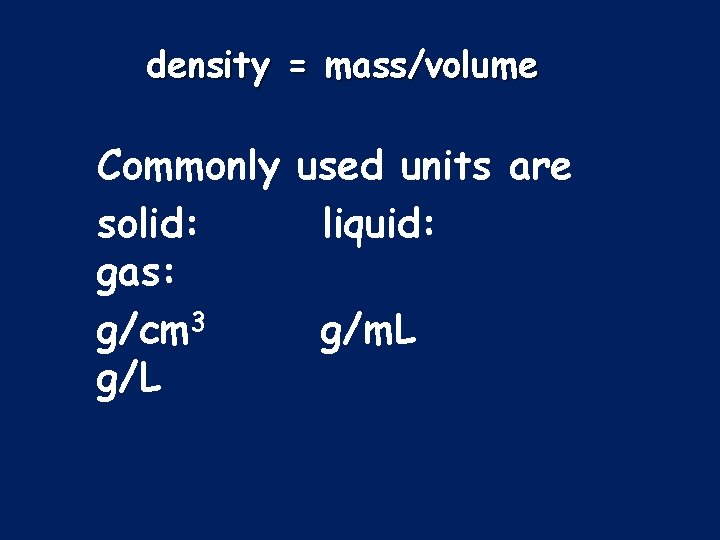
density = mass/volume Commonly used units are solid: liquid: gas: g/cm 3 g/m. L g/L

Example 36: Find the density of a piece of Al with a volume of 4. 0 cm 3 and a mass of 10. 8 g. d = m/v d = 10. 8 g/ 4. 0 cm 3 (yes, you must show units in your work) 2. 7 g/cm 3

Example 157: A 40. 0 cm 3 sample of quartz has a density of 2. 65 g/cm 3. What is the mass of the quartz sample? d = m/v Rearrange your equation first! m = d x v m = 2. 65 g/cm 3 x 40. 0 cm 3 m = 106 g

Example 2056: The density of a sample of cork is 0. 24 g/cm 3. What is the volume of this sample if it has a mass of 36. 2 g? d = m/v Rearrange equation! v = m/d v = __36. 2 g_ 0. 24 g/cm 3 V = 150 cm 3 (2 sigfigs!)

Diagram: of a cube Now, draw that picture that is 1 cm x 1 cm again. 1 cm What is the volume of this box? 1 cm 3 or 1 m. L If you fill the box with water, what is the MASS of the water? 1 g

1 cm Fun facts. What would be the mass of the cube if it were filled with aluminum? 2. 7 g gold? ? 19. 3 g Air? 0. 00119 g Mercury (Hg)? One of the heaviest liquids known.

WATER AND DENSITY Water has a density of ~1 g/m. L. 1 m. L of water has a mass of 1 gram. Mass of 10 m. L of water? 10 g Volume of 25 g of water? 25 m. L Water is densest at 4ºC, therefore, ice floats.

That’s the end of the content for Unit 1: Science 101