THE SHELL MODEL A brief introduction D S

THE SHELL MODEL A brief introduction D S Judson

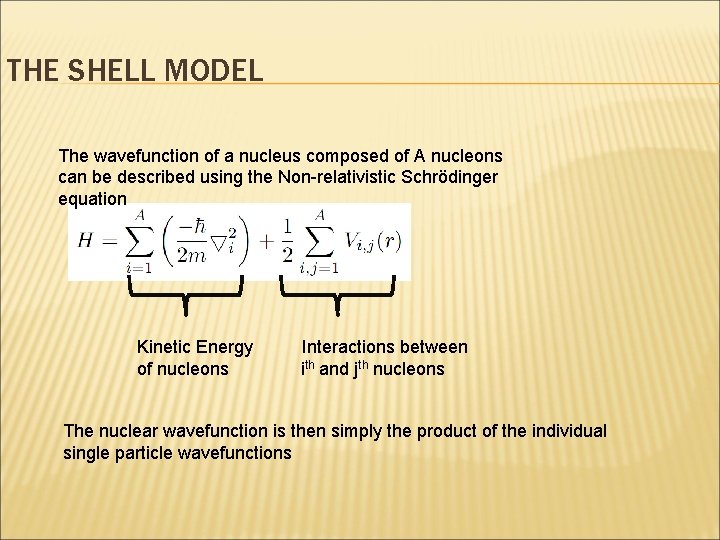
THE SHELL MODEL The wavefunction of a nucleus composed of A nucleons can be described using the Non-relativistic Schrödinger equation Kinetic Energy of nucleons Interactions between ith and jth nucleons The nuclear wavefunction is then simply the product of the individual single particle wavefunctions

THE SHELL MODEL In practice, the Schrödinger equation is not much use for describing the nuclei we are typically interested in looking at The nucleus is a finite, many body problem Such a calculation is far too computationally intensive Interactions between nucleons are not fully understood Analytical solution not possible for A >~ 16 - full scale sd shell calculations are possible Even if the calculations could be performed, the results would be so complex they

THE SHELL MODEL To allow a useful description of the nuclear wavefunction to be developed, a number of simplifications / assumptions have to be made. • Assume a spherical inert closed shell core which plays no role in low energy excitations • Assume higher lying orbitals play no role either • The low energy properties of the nucleus are then determined by the valence nucleons • Reduce the multi-nucleon interactions to an average, attractive, central potential E. g. Woods-Saxon potential • Assume nucleons undergo independent motion within this potential

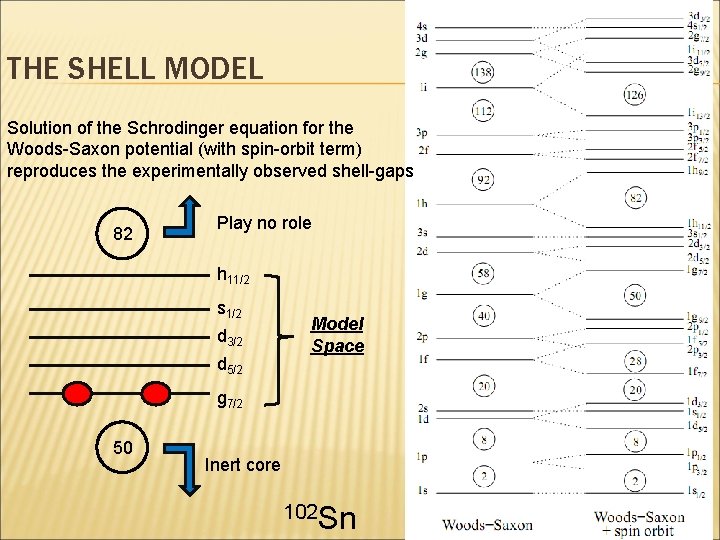
THE SHELL MODEL Solution of the Schrodinger equation for the Woods-Saxon potential (with spin-orbit term) reproduces the experimentally observed shell-gaps 82 Play no role h 11/2 s 1/2 d 3/2 d 5/2 Model Space g 7/2 50 Inert core 102 Sn

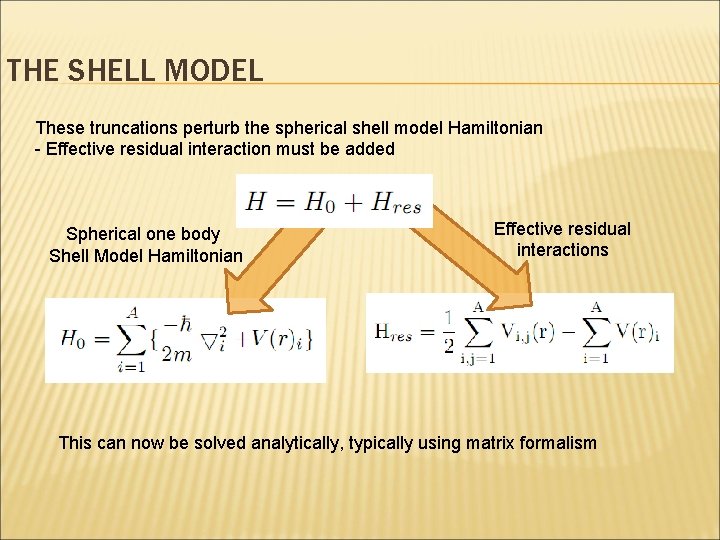
THE SHELL MODEL These truncations perturb the spherical shell model Hamiltonian - Effective residual interaction must be added Spherical one body Shell Model Hamiltonian Effective residual interactions This can now be solved analytically, typically using matrix formalism

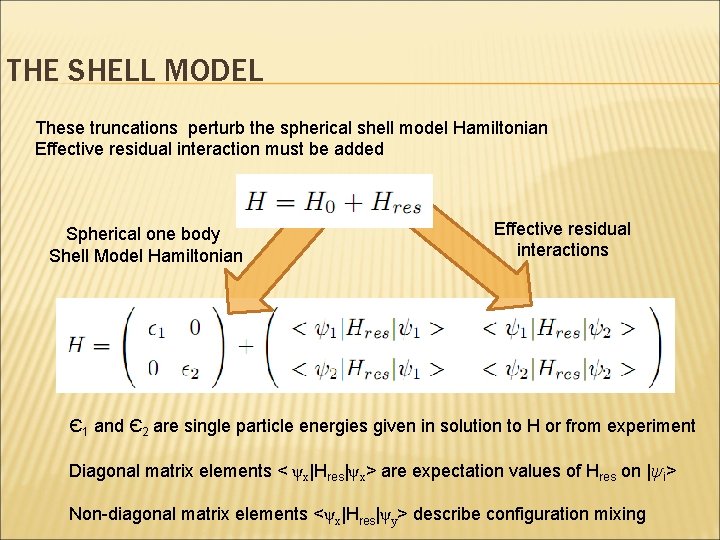
THE SHELL MODEL These truncations perturb the spherical shell model Hamiltonian Effective residual interaction must be added Spherical one body Shell Model Hamiltonian Effective residual interactions Є1 and Є2 are single particle energies given in solution to H or from experiment Diagonal matrix elements < ψx|Hres|ψx> are expectation values of Hres on |ψi> Non-diagonal matrix elements <ψx|Hres|ψy> describe configuration mixing

THE SHELL MODEL The resultant matrix is diagonalised to determine eigenvalues / eigenvectors • Eigenvalue give the energy of the state • Eigenvectors describe the wavefunction of the state A numerical example Calculate the energy of the first two 0+ states in 42 Ca • Assume can be described as a closed core of 40 Ca + 2 valence neutrons • Assuming a restricted model space of 1 f 7/2 and 2 p 3/2 orbitals The (ν 2 f 7/2) and (ν 2 p 3/2) Jπ = 0+ states are the basis vectors |ψi> 50 Restricte d Model Space g 9/2 p 1/2 f 5/2 p 3/2 f 7/2 20 Full Model Space

THE SHELL MODEL The resultant matrix is diagonalised to determine eigenvalues / eigenvectors • Eigenvalue give the energy of the state • Eigenvectors describe the wavefunction A numerical example. . . Calculate first two 0+ states in 42 Ca • Assume can be described as a closed core of 40 Ca + 2 valence neutrons • Assuming a model space of 1 f 7/2 and 2 p 3/2 orbitals The (ν 2 f 7/2) and (ν 2 p 3/2) Jπ = 0+ are the basis vectors |ψi> S. P. Es and matrix elements are taken from fpd 6 interaction Shell Model Hamiltonian (Single particle energies) Effective interactions (matrix elements) Diagonalisation gives Elevel and wavefunctions

THE SHELL MODEL 3. 118 0+ 5. 639 -2. 521 0+ 42 Ca Nu. Shell uses the Lanczos method of diagonalisation which is slightly quicker!

THE SHELL MODEL The ‘three pillars’ of the shell model 1) A ‘good’ (realistic) model space 2) Effective interactions adapted to the model space 3) A code that makes it possible to solve these equations Difficulties • Effective interactions / matrix elements are derived for nuclei near closed shells • Nuclei far from closed shell exhibit structure effects not accounted for in model • Single particle energies are not well known away from closed shells • The more valence nuclei, the larger the matrix to be diagonalised, the harder the calculation computationally • The larger the model space the larger the matrix also

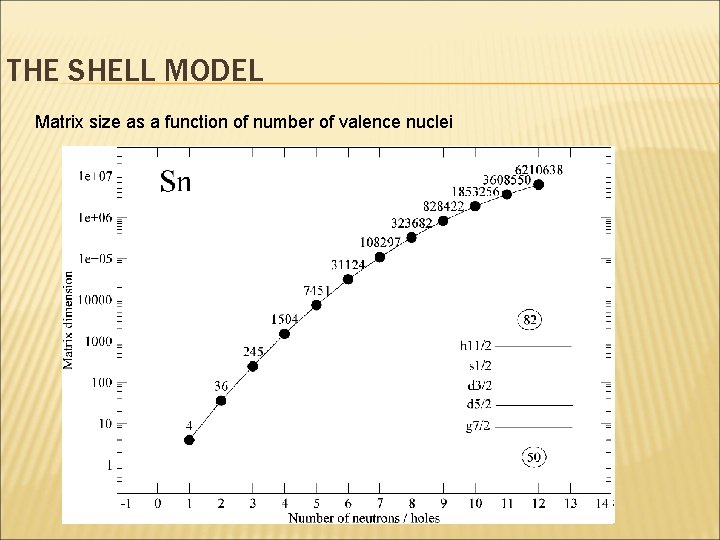
THE SHELL MODEL Matrix size as a function of number of valence nuclei

THE SHELL MODEL The size of the Hamiltonian matrix can be reduced by reducing the model space I. e. reducing the number of orbitals that the nucleons can occupy and / or reducing the number of nucleons that can occupy a given orbital. HOWEVER - Non physical restrictions will give non physical results! Just because the computer gives a result does not mean the calculation is a succ