The Shell Method Volumes by Cylindrical Shells By

The Shell Method Volumes by Cylindrical Shells By Christine Li, Per. 4

Conceptually the same as the washer method w Do not sum up the volumes of the washers w Instead of summing the volumes of washers you sum up the volumes of shells

Example 1 w Question: n Find the volume of the solid obtained by rotating about the y-axis the region bounded by y = x 2 and between x = 1 and x=2

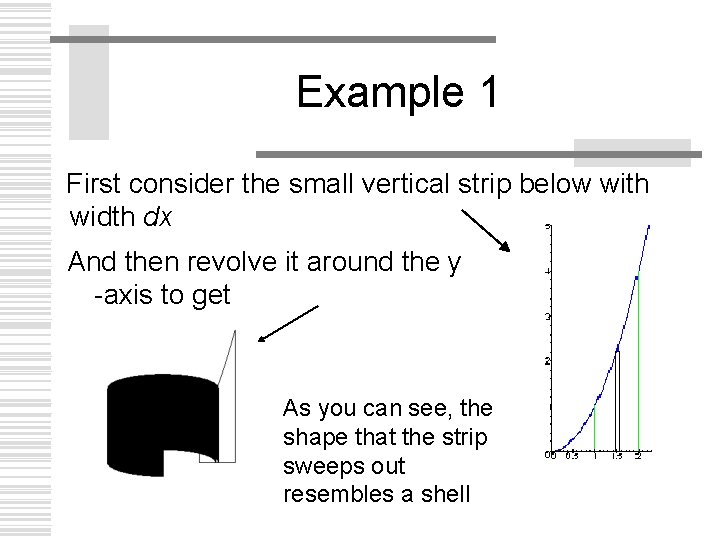
Example 1 First consider the small vertical strip below with width dx And then revolve it around the y -axis to get As you can see, the shape that the strip sweeps out resembles a shell

Example 1 w The next step is to calculate the volume of this single shell. Since thickness is dx, all you need is to calculate the surface area of the shell n volume = thickness x surface area

Example 1: Surface Area of a Shell w First, cut the shell and unroll it, and get the following picture h <-----(2 pi)r----> w Since (2 pi)r is the length, h is the width, and dx is the depth, the volume of this shell is (2 pi)rh dx.

Example 1: But what are r and h? h <-----(2 pi)r----> w We see that the distance from the y-axis to the strip is x n Therefore, r = x w Since the height of the strip is the distance from the x-axis to the curve (y = x 2) we see that h = x 2 w The volume of a single shell is (2 pi)x 3 dx

Example 1: Approximating the volume w Now approximate the volume of the solid of revolution by summing the volumes of all the shells from x = 1 to x = 2 w We then take the limit as the number of shells tends to infinity n to find the volume of the solid of revolution

Example 1: Final Step w The limit converges to the following integral 2 2 pi x 3 dx = (15 pi)/2 1 w In general, we have the following formula for the volume of a solid of revolution using the shell method : Where r is the radius of the shell, h b a (2 pi)rh dx is the height of the shell and a and b are the bounds on the domain of x.

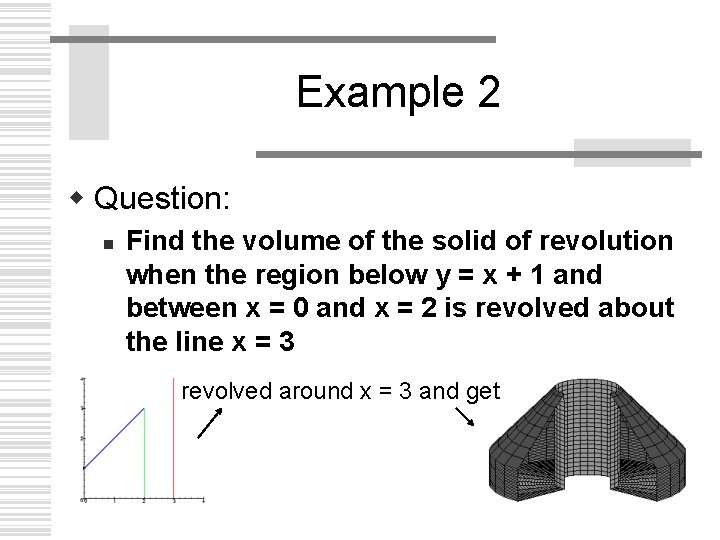
Example 2 w Question: n Find the volume of the solid of revolution when the region below y = x + 1 and between x = 0 and x = 2 is revolved about the line x = 3 revolved around x = 3 and get

Example 2: But what are r and h? w Here we take a vertical strip with thickness dx to get a shell w The radius is the distance from the curve ( y = x + 1) to the line x = 3 n The radius is r = 3 - x (remember the radius has to be in terms of the variable x). w The height is the distance from the x-axis to the curve ( y = x + 1) n Since y = x + 1, the height of the strip is h = x + 1

Example 2: Final Step w Use the shell method formula w and remember that the area is bounded between x = 0 and x = 2 n Therefore, set 0 to be the lower limit, and 2 as the upper limit. 2 (2 pi)(3 - x)(x + 1) dx 0 = (44 pi)/3