The Sequence of Fibonacci Numbers and How They

The Sequence of Fibonacci Numbers and How They Relate to Nature November 30, 2004 Allison Trask

Outline l History of Leonardo Pisano Fibonacci l What are the Fibonacci numbers? ¡ Explaining the sequence ¡ Recursive Definition l Theorems and Properties l The Golden Ratio l Binet’s Formula l Fibonacci numbers and Nature

Leonardo Pisano Fibonacci Born in 1170 in the citystate of Pisa l Books: Liber Abaci, Practica Geometriae, Flos, and Liber Quadratorum l Frederick II’s challenge l Impact on mathematics l http: //www-gap. dcs. st-and. ac. uk/~history/Mathematicians/Fibonacci. html

What are the Fibonacci Numbers? 1 1 2 3 5 8 13 21 34 55 89 … F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11. . . Recursive Definition: F 1=F 2=1 and, for n >2, Fn=Fn-1 + Fn-2 l For example, let n=6. Thus, F 6=F 6 -1 + F 6 -2 F 6=F 5 + F 4 F 6=5+3 So, F 6=8 l

Theorems and Properties l Telescoping Proof Theorem: For any n N, F 1 + F 2 + … + Fn = Fn+2 - 1 Proof: Observe that Fn-2 + Fn-1 = Fn (n >2) may be expressed as Fn-2 = Fn – Fn-1 (n >2). Particularly, F 1 = F 3 – F 2 = F 4 – F 3 = F 5 – F 4 … Fn-1 = Fn+1 – Fn Fn = Fn+2 – Fn+1 When we add the above equations and observing that the sum on the right is telescoping, we find that: F 1 + F 2 + … + Fn = F 1 + (F 4 – F 3) + (F 5 – F 4) + … + (Fn+1 – Fn) + (Fn+2 – Fn+1) = Fn+2 +(F 1 -F 3)= Fn+2 – F 2 = Fn+2 – 1

Theorems and Properties l Proof by Induction Theorem: For any n N, F 1 + F 2 + … + Fn = Fn+2 – 1. 1) Show P(1) is true. F 1 = F 2 = 1, F 3 = 2 F 1 = F 1+2 – 1 F 1 = F 3 – 1 F 1 = 2 -1 F 1 = 1 Thus, P(1) is true.

Theorems and Properties 2) Let k N. Assume P(k) is true. Show that P(k +1) is true. Assume F 1 + F 2 + … + Fk = Fk+2 – 1. Examine P(k +1): F 1 + F 2 + … + Fk+1 = Fk+2 – 1 + Fk+1 = Fk+3 – 1 Thus, P(k +1) holds true. Therefore, by the Principle of Mathematical Induction, P(n) is true ∀n N.

Theorems and Properties l Combinatorial Proof l What is a tiling of an n-board – what is fn? ¡ fn=Fn+1 l How many ways can we tile an 4 -board? ¡ f 4=F 5

Theorems and Properties Identity 1: For n 0, f 0 + f 1 + f 2 + … + fn = fn+2 – 1. Question: How many tilings of an (n +2)-board use at least one domino? Answer 1: There are fn+2 tilings of an (n+2)-board. Excluding the “all square” tiling gives fn+2 – 1 tilings with at least one domino. Answer 2: Condition on the location of the last domino. There are fk tilings where the last domino covers cells k +1 and k +2. This is because cells 1 through k can be tiled in fk ways, cells k +1 and k +2 must be covered by a domino, and cells k+3 through n+2 must be covered by squares. Hence the total number of tilings with at least one domino is f 0 + f 1 + f 2 + … + fn (or equivalently fk).

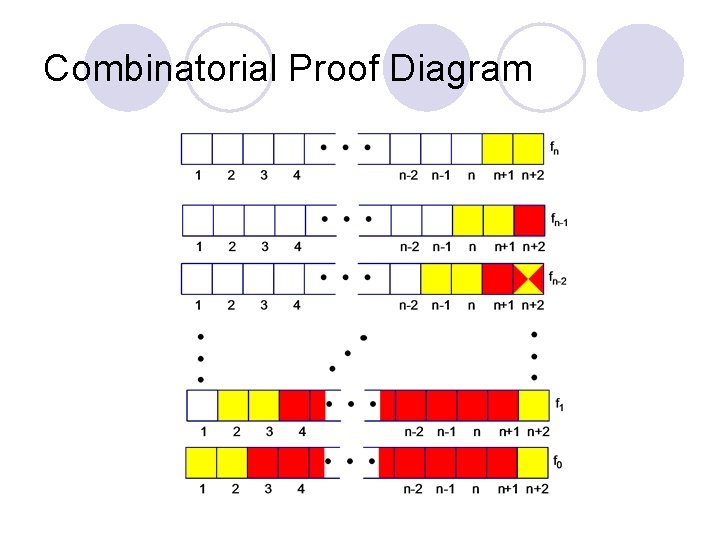
Combinatorial Proof Diagram

The Golden Ratio l What is the Golden Ratio? l Satisfies the equation l Positive Root: l Negative Root:

Binet’s Formula l What is Binet’s Formula? For any l What is the importance of this formula? l Direct and Combinatorial Proof l Let’s do an example together where

Binet’s Formula Therefore, when , we find that when using Binet’s formula, equals 832, 040. amazingly

Binet’s Formula l Combinatorial Method ¡ Probability ¡ Proof by Induction ¡ Telescoping Proof ¡ Counting Proof ¡ Convergent Geometric Series l Together, the above yield Binet’s Formula

Fibonacci numbers and Nature l Pinecones l Sunflowers l Pineapples l Artichokes l Cauliflower l Other Flowers http: //www. mcs. surrey. ac. uk/Personal/R. Knott/Fibonacci/fib. html

Fibonacci numbers and Nature http: //www. mcs. surrey. ac. uk/Personal/R. Knott/Fibonacci/fib. html

Fibonacci numbers and Nature http: //www. mcs. surrey. ac. uk/Personal/R. K nott/Fibonacci/fib. html

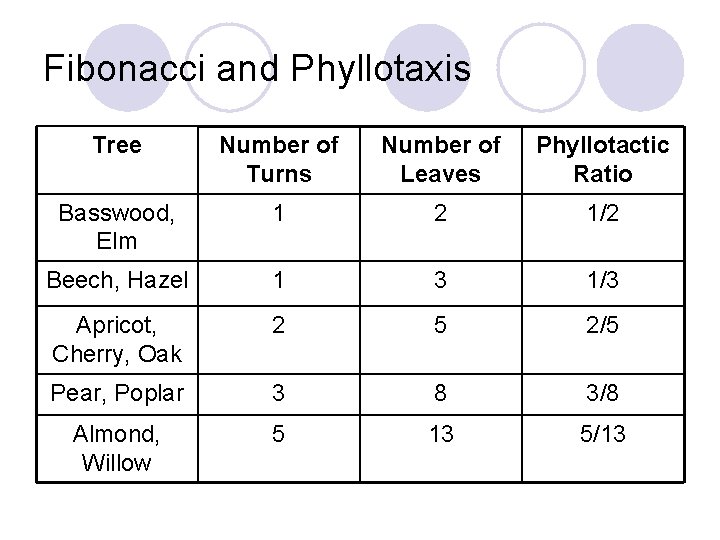
Fibonacci and Phyllotaxis Tree Number of Turns Number of Leaves Phyllotactic Ratio Basswood, Elm 1 2 1/2 Beech, Hazel 1 3 1/3 Apricot, Cherry, Oak 2 5 2/5 Pear, Poplar 3 8 3/8 Almond, Willow 5 13 5/13

Fibonacci and Phyllotaxis l Thus, we can conclude that approximates

Further Research Questions l Looking at Binet’s Formula in more detail l Looking at Binet’s Formula in comparison with Lucas Numbers ¡ Similarities? ¡ Differences? l Fibonacci and relationships with other mathematical concepts?

Thank you for listening to my presentation!