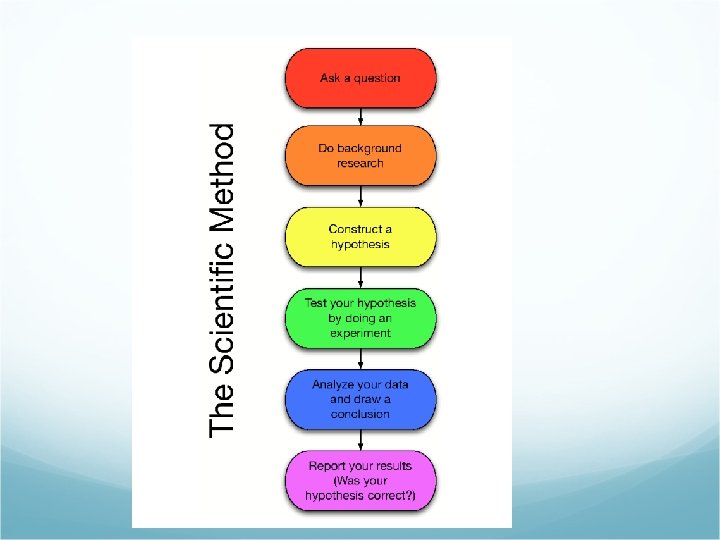
The Scientific Method A Quest for the Facts

The Scientific Method A Quest for the Facts!

Characteristics of Science is the pursuit of FACTUAL knowledge about the universe and the processes the govern it. Science is NOT the pursuit of TRUTH. Therefore the Scientific Method is not appropriate for questions about Religion, Art, Philosophy, or the supernatural. The Scientific Method is the accepted process used in Chemistry, Physics, Biology, and Earth/Space Science that is applied in the same manner.

Properties That Set Science Apart Scientific knowledge is obtained through empirical evidence. Scientific knowledge is developed over many years from many sources and is open to change due to the introduction of new empirical evidence. Scientific results must be reproducible using the same method by other members of the Scientific community. Scientific Theories are well supported explanations (why things work) and Laws are well supported descriptions (how things work).

Accuracy vs. Precision

Accuracy vs. Precision Accuracy is how close your measurement is to the true value. Precision is how close together your measurements are to each other.

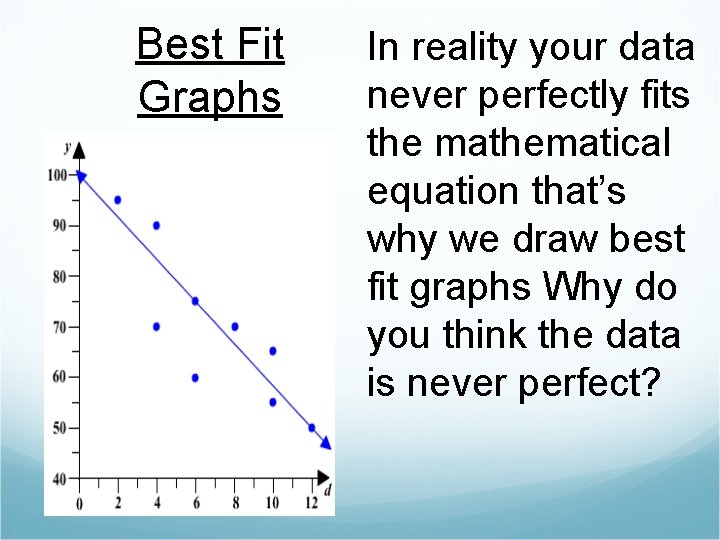
Best Fit Graphs In reality your data never perfectly fits the mathematical equation that’s why we draw best fit graphs Why do you think the data is never perfect?

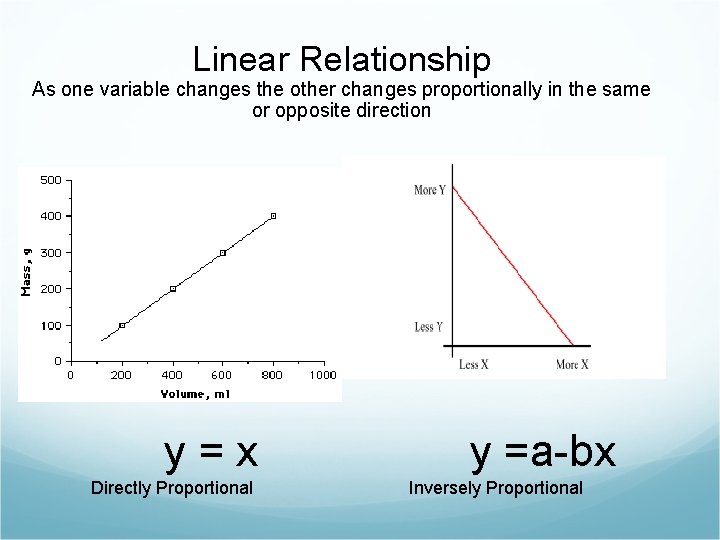
Linear Relationship As one variable changes the other changes proportionally in the same or opposite direction y=x Directly Proportional y =a-bx Inversely Proportional

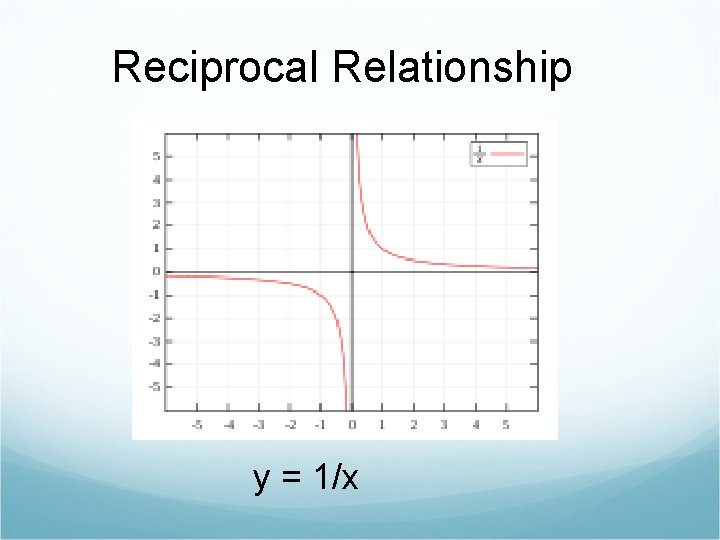
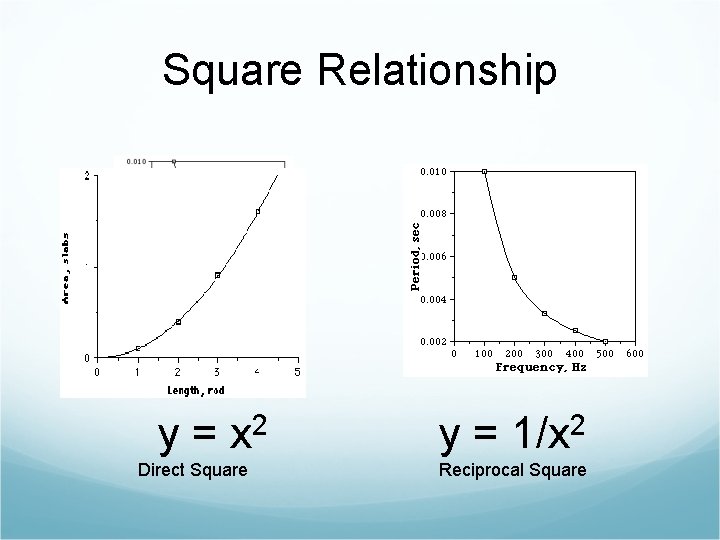
Reciprocal Relationship y = 1/x

Square Relationship y= 2 x Direct Square y= 2 1/x Reciprocal Square

DATA and MEASUREMENT • • When numbers are used as data (quantitative data) we must understand what we mean by them. The numbers we use are from experiments in which things are measured. Whenever you are describing what is observed in an experiment (without numbers) you are recording Qualitative Data. Size, shape, color, texture, direction, speed, increasing, decreasing, etc. are all examples of qualitative data.

DATA and MEASUREMENT • Some things can be measured exactly while others cannot. • • People can be measured exactly because it is done by one. However, other things like the length of a piece of paper cannot be measured exactly. Your measurement depends on how precise your instrument is.

• • One of the rulers above (when measuring in inches) is more precise. Which one and why? Why is this important?

SIG FIG RULES There a few rules we will learn to determine the number of significant figures in a number: • Numbers for data that are counted one by one have INFINITE significant figures. • All numbers 1 -9 are significant

SIG FIG RULES (Cont’d) • Zero’s are significant EXCEPT when: • Trailing zeros: The number is greater than 1, there is no decimal and they are at the end of a number. • EX: 3, 000 (The last 3 zero’s are NOT significant) • EX: 3, 000. (These zeros ARE significant) • Leading Zeros: The number is less than 1 and they appear at the front of a number. • EX: 0. 0002 (The first 4 zeros are NOT significant) • EX: 0. 000200 (The first 4 zeros are NOT significant but the last two ARE. ) • Middle zeros: Zeros in between to significant digits are always significant. • EX: 2020 (the middle zero is significant but the last one is not) • EX: 0. 000040010 (the leading zeros are not significant but the middle and trailing zeros are)

PRACTICE TIME State the number of significant numbers in each set: 1. 0. 020003 = ____ 2. 0. 0002300 = ____ 3. 0. 000103 = ____ 4. 0. 0009 5. 0. 0000033 = ____ 6. 0. 000900 = ____ 7. 2, 000= ____ 8. 500. = ____ 9. 500. 000 = ____ 10. 8020 = ____ 11. 90, 000 = ____ 12. 208, 030 = ____ 13. 8, 000. = ____ 14. 80, 200 = ____ 15. 23. 00 = ____ 18. 0. 000 = ____ 16. 3340. 0 = ____ 17. 90 = ____ 19. 2000 = ____ 20. 200, 000 = ____ 21. 2000. 22. . 8070 = ____ 23. 0. 02020 = ____ 24. 0. 03003 = ____

SCIENTIFIC NOTATION Instead of using standard notation scientists write numbers in scientific notation. This system uses the base 10 as a multiplying factor to move the decimal place around. X 100 = times 1 X 101 = times 10 X 10 -1 = times. 1 X 102 = times 100 X 10 -2 = times. 01 And so on…The base 10 moves the decimal around. So why do we use this? The answer is simple. In science we commonly have to use numbers that are very large or very small and scientific notation is easier to use than standard notation. For example the number of atoms in 12. 01 grams (1 mole) of carbon is: 602, 000, 000, 000 This would be a pain to write so instead we use: 6. 02 X 1023

CONVERT THE STANDARD NOTATION INTO SCIENTIFIC (WATCH YOUR SIG FIGS) 1. 660, 000 = _____ 2. 8, 000. = ______ 3. 9050 5. = _____ 4. 5, 001 = ______ 2. 000 = _____ 6. 4403. 0 = ______ 7. 0. 0120 = _____ 8. 0. 0500 = ______ 9. 0. 00202 = _____ 10. 0. 0020 = _____

CONVERT THE SCIENTIFIC NOTATION TO STANDARD (WATCH YOUR SIG FIGS) 1) 6. 02 X 10 -4 = __________ 2) 2. 02 X 10 -8 = __________ 3) 2. 00 X 10 -5 = __________ 4) 9. X 10 -2 = ___________ 5) 9 X 100 = ____________ 6) 5. 0089 X 106 = __________ 7) 3. 0 X 105 = ___________ 8) 3 X 106 = ____________ 9) 5. 000 X 101 = __________ 10) 4. 00 X 102 = ___________

ROUNDING What is rounding? 1) 15. 6 It comes from the idea that 2) 15. 6 some numbers are irrelevant or not significant and therefore not reliable. 3) 690 In science, we do not 4) 5, 555 round like math. We must round to the appropriate 5) 8. 12 X 104(2) number of sig figs. (2) (1) (2) 6) 9. 5 X 102 (1) 7) 4. 5 X 104 (1)

ROUND THE VALUE TO THE NUMBER OF SIG. FIGS. INDICATED BY THE PARENTHESIS. 1) 555. 5 (1)______ 2) 7. 586500 (4)______ 3) 650 (1)_______ 4) 0. 0055 (2)______ 5) 1. 500 (1)____ 6) 0. 3400 (1)______ 7) 428. 09 (3)______ 8) 666, 500. (4)______ 9) 0. 7500 (1)_____ 10) 0. 0630 (1)______ 11) 0. 4355 (1)______ 12) 9. 50 (1)_____ 13) 995. (2)_______ 14) 199, 500 (3)______ 15) 2. 9995 (4)_______

SIG FIG CALCULATIONS As has been discussed, numbers are very important and their reliability is crucial when using them for practical applications. When doing science we often take the data that we have measured and manipulate it to find a multitude of other information. In other words, we take the numbers from our experiment and we will add, multiply, subtract, and divide them in order to calculate other derived quantities. However, the problem arises in that all numbers are NOT created equally.

ADDITION & SUBTRACTION Look at all the numbers that are in your calculation and determine which has the least number of decimal places. Your answer should have the same number of decimal places as this one. (Units must be the same) EX: 1. 230 g +12. 5 g + 25. 36521 g = 39. 09521 Final answer rounded = 39. 1 g

MULTIPLICATION & DIVISION Look at all the numbers that are in your calculation and determine which has the least amount of significant figures. Your answer should have the same number of significant figures as this one. Treat units like variables in algebra EX: 3, 000. m 3 = 300 m = 3. 0 X 102 m 10. m 2 EX: (12. 220 ft) X (11 ft) = 13 4. 42 ft 2 = 130 ft 2

CALCULATION PRACTICE 1. 654. 0 g 5/6 g = __________ 2. (5500 m-9)(56. m) = _________ 3. 8. 632 nm+ 8. 3 nm – 30. 0 nm = ____ 4. 18 g +6. 80 L+0. 050 L– 226 =____ 5. (60. 0 g)/(230 cm 3) - 0. 0520 g/cm 3 = ______ 6. (0. 020 ml)(300. 560 ml) + 1 ml 2 =_____ 7. 6. 9 X 107 nm 3 / 4. 00 X 107 nm = _______ 8. (1 X 10 7 kg 3)(2. 45 X 10 -4 ft-3) = ____ 9. 2. 55 X 102 ml 4 + 6. 6 X 103 ml 4 = _______ 10. 4 X 10 -2 ft 2 - 2. 00 X 10 -3 ft-3 = _____ 11. (6. 9 X 107 Kg 3 / 4. 00 X 106 Kg 3) - 8 X 101 kg- 2. 3 X 101 kg 3________

Rules for Conversions 1. Write down the number and unit to be converted on the left. (Starting number and unit) 2. Determine the desired unit (finish unit). 3. Find key(s) that connect the units using the prefixes. (Use your key maker. ) 4. Write factor(s) (i. e. brackets) so that the units cancel. 5. Solve (do the math) and check your sig. figs.

Standard Key For Metrics Exponent 1 __|__ = 1 x 10_ __ Prefix Base Ex: for cm the key would be 1 cm = 1 x 10 -2 m No matter what order the units are in your problem, the key will always look the same. If I want to change 25. 0 m to cm do the following using the key from above: