The Science of Flight Seriously How do Airplanes

The Science of Flight: Seriously, How do Airplanes Fly? National Science Teachers Association Conference San Francisco, California – March 11, 2011 Phoenix, Arizona - Dec. 3 rd, 2009 Colorado Science Conference Denver, Colorado USA – Nov. 19 th, 2010

Introduction: Who is David Esker • BS & MS in Physics • College Physics Instructor • Author of Dinosaur. Theory. com

Science of Flight Outline 1. Introduction to Flight and the Paradox of Flying Pterosaurs 2. How wings generate lift 3. Deriving the Power for Flight Equations 4. Applying the Power for Flight Equations to various flyers 5. Review key concepts

Over a hundred years without a theory to explain flight Sources of Confusion: • Flying gigantic pterosaurs make no sense • Galileo’s Square-Cube Law left out of science education • Bogus Equal Transit Time / Bernoulli’s Principle Explanation

Equal transit statement is wrong. • Equal transit statement is not a conservation law of physics. • Above and below airflows do not reach the back of the wing at the same time. • Cause and effect of Bernoulli’s is reversed: the air flows faster over the top because the pressure is less.

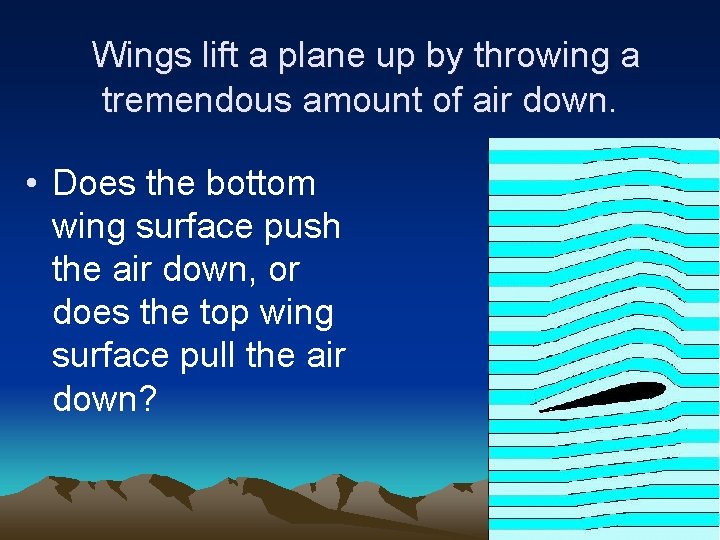
Wings lift a plane up by throwing a tremendous amount of air down. • Does the bottom wing surface push the air down, or does the top wing surface pull the air down?

Pushing the Air Down • A kite is lifted up by the large bottom surface area pushing the wind down. • The unsuccessful early aviation pioneers thought that large surface area wings would work best in generating lift by pushing the air down.

• They were wrong. • In normal flight, lift is not a function of the surface area of the wing.

The wings of most planes do not generating lift by pushing air down. • The exception to this is the supersonic jets that have delta wings that help them to make safe landings. • The broad surface area delta wings allow jets the ability to make power stall landings.

The Wright brothers got it right. • The top wing surface pulls the air down • A plane is lifted up as a result of the reactionary force that comes from throwing the air down.

Coanda Effect • Because a fluid sticks to a surface it follows the shape of the surface. • Air is a fluid that sticks to the top wing surface. • Air is thrown down as it follows the shape of the wing.

The pulling effect extends far above the wing. • The effective area of air being pulled down is approximately equal to ½ b 2. • b is the wingspan.

Lift is proportional to the wingspan squared, not the surface area of the wing. • Long Wings Produce the Most Lift.

Broad Wings Facilitate Safe Landings. • Broad Wings make it harder for the airflow to break away from the wing. • Decrease the possibility of a stall.

Stalling is Bad • Lift can be increased by increasing the Angle of Attack but 1. This also increases the drag 2. Too much AOA will produce a stall.

Summary of this Section • Wings lift planes up by throwing a tremendous amount of air down. • Because the air flow sticks to the wing, the top wing surface is able to pull the air down so as to lift the wings up. • Effective area A = ½ b 2.

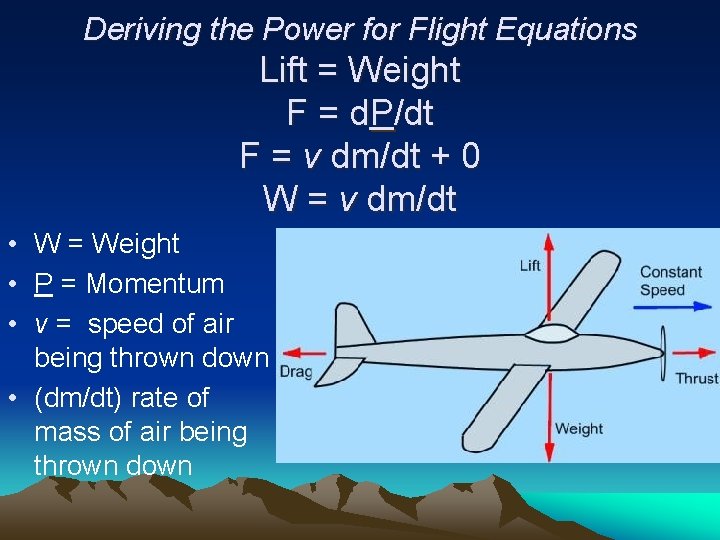
Deriving the Power for Flight Equations Lift = Weight F = d. P/dt F = v dm/dt + 0 W = v dm/dt • W = Weight • P = Momentum • v = speed of air being thrown down • (dm/dt) rate of mass of air being thrown down

W = v dm/dt = ρ d. V/dt dm/dt = ρ A dx/dt dm/dt = ρ A v W = v ρ (1/2 b 2) v • Where W is weight, v is the speed that the air is being thrown down, ρ is the air density, b is the wingspan, and v is the relative speed of the plane through the air.

Power Required for Lift Equations from previous slide dm/dt = ρ (½ b 2 ) v • • • E = ½ m v 2 P = d. E/dt PL = d(½ m v 2)/dt PL = ½ (dm/dt) v 2 PL = W 2 / (ρ b 2 v) & v = 2 W / (ρ b 2 v)

Power to Overcome Drag • • FD = ½ C A ρ v 2 PD = F v PD = ½ C A ρ v 3 PD is the power required to overcome drag C is the aerodynamic drag coefficient, A is the plane’s front facing area, ρ is the air density, and v is the plane’s relative speed through the air.

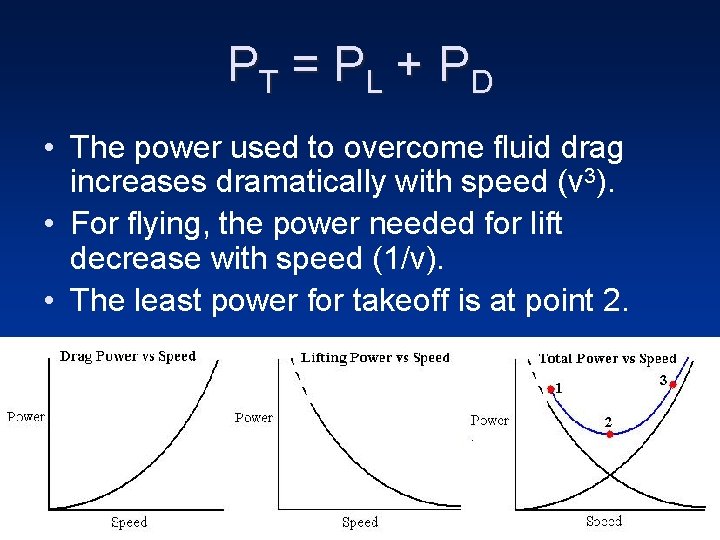
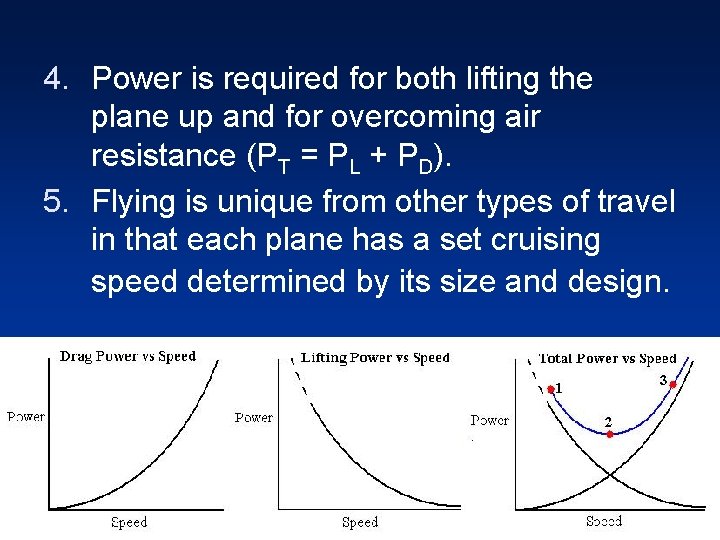
PT = P L + P D • The power used to overcome fluid drag increases dramatically with speed (v 3). • For flying, the power needed for lift decrease with speed (1/v). • The least power for takeoff is at point 2.

To find the minimum power and takeoff speed take the derivative. • PT = P L + P D • PT = W 2 / (ρ b 2 v) + ½ C A ρ v 3 • d. PT/dv = 0 • Results: • vmin-P = [(2 W 2) / (3 C A b 2 ρ2)]1/4 • Pmin = 4/3 [W 2 / (ρ b 2 vmin-P)]

The Holy Grail of Aerodynamics • vmin-P = [(2 W 2) / (3 C A b 2 ρ2)]1/4 • Pmin = 4/3 [W 2 / (ρ b 2 vmin-P)] • Esker’s Equations of Flight are directly derived from physics principles. • Results are general to both airplanes and flying vertebrates.

The minimum requirement for flight is a 1. 0 power ratio. Flyer Takeoff Speed (m/s) Minimum Power (k. W) Relative Power Ratio Cessna 172 28 37 2. 3 Sopwith Camel 21 30 2. 3 Wright Flyer 14 5. 7 1. 1

Esker’s Flight Equations are precise and insightful. • vmin-P = [(2 W 2) / (3 C A b 2 ρ2)]1/4 • Pmin = 4/3 [W 2 / (ρ b 2 vmin-P)] • Example: first equation gives 14 m/s as the Wright Flyer’s takeoff speed. • But according to historical records 4 to 5 m/s was the Wright brother’s overland speed. • The difference of 10 m/s was the headwind speed at Kitty Hawk, NC on Dec. 17, 1903.

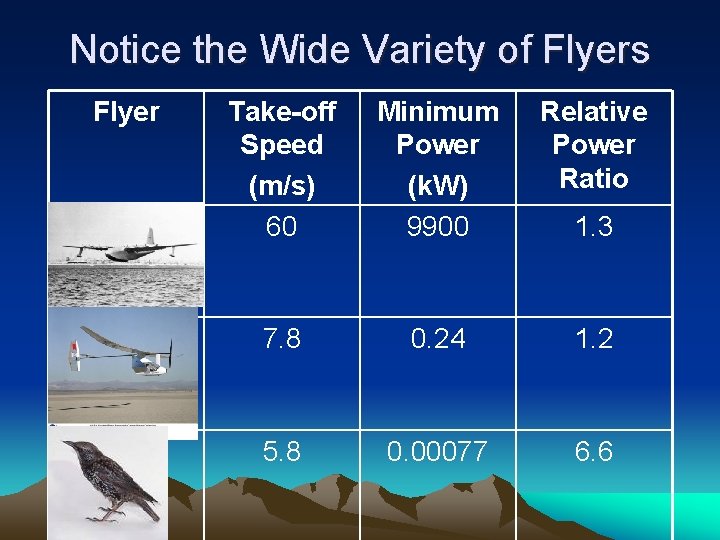
Notice the Wide Variety of Flyers Flyer Spruce Goose Human Flight Starling Take-off Speed (m/s) 60 Minimum Power (k. W) 9900 Relative Power Ratio 7. 8 0. 24 1. 2 5. 8 0. 00077 6. 6 1. 3

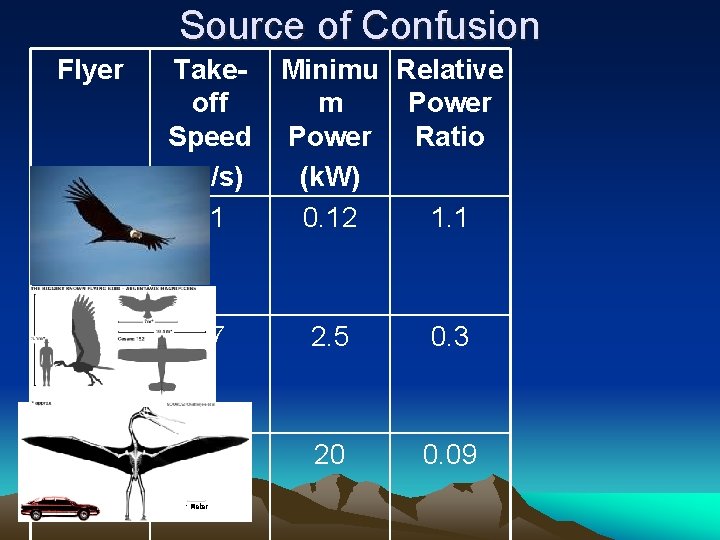
Source of Confusion Flyer Condor Takeoff Speed (m/s) 11 Minimu Relative m Power Ratio (k. W) 0. 12 1. 1 Argenta vis 17 2. 5 0. 3 Quetzalcoatlus 18 20 0. 09

So how did the Argentavis and Quetzalcoatlus fly? • The answer is in the equations: • vmin-P = [(2 2 W) / (3 C A 2 b 2 1/4 ρ )] • Pmin = 4/3 [W 2 / (ρ b 2 vmin-P)]

Key Points Regarding Flight 1. Wings lift a plane up by throwing air down. 2. The top wing surface pulls the air down as the air stream following the profile of the wing.

3. Lift is not directly related to wing area but rather it is a function of the wingspan squared (½ b 2).

4. Power is required for both lifting the plane up and for overcoming air resistance (PT = PL + PD). 5. Flying is unique from other types of travel in that each plane has a set cruising speed determined by its size and design.

6. Larger planes fly faster than smaller planes and they require much more power. 7. Jets have swept wings so that their wing tips are behind the front created by the sound wave.

8. Because of the much greater power requirement and the fact that relative strength and relative power decreases with size, larger birds have greater difficulty in flying.

9. The squeeze between requiring greater power but having less relative power is what limits the size of flying birds and bats.

10. The Power for Flight Equations 1) advances our understanding of aerodynamics and 2) shows that Argentavis and Quetzalcoatlus could not have flown in today’s atmospheric environment.

Further Reading / References • The Simple Science of Flight - Henk Tennekes • How Airplanes Fly - Anderson & Eberhardt • Data from Seabirds and Implication for Flying Pterosaurs - Katsufumi Sato • Dinosaur. Theory. com – David Esker

End of Presentation on The Science of Flight Thank you David Esker