The Saddam and George show Blair Lets move

¾: The Saddam and George show • Blair: Let's move on. Saddam, are you willing to destroy your stockpile of Samoud 2 missiles in accordance with UN weapons inspectors' orders? • Saddam: I explain to you now that if Iraq possessed these so-called weapons, we would never destroy them, but since we do not have any such weapons, we are happy to comply, even though these nonexistent weapons certainly do not exceed the proscribed range of 150 kms. I've tested them myself, and we don't have any. • Blair: The final question is for George Bush. Mr President, is there any way that Saddam Hussein can avoid war, and what steps must he now take in order to reach a negotiated solution? • Bush: Listen to me. It's very simple. First Saddam must compile 200% with the UN inspectorers, and I mean activated compilation, not passivist compilation. Second, he must disarm fully, in keeping with UN revelation 1441 and the next one coming, 1441 B, which will require him to disarm even more fully that. Then he must destroy all Samoud missiles and any other weapons of mass destruction he is found, or not found, to be possessive of, without being asked. Finally, there is one more task he must perform, which I am not at liberty to revulge. And even that will not be enough. Tim Dowling; Guardian 2/25

3/4 A bit on the EBL/Memo connection Alternative encoding substrates Direct encodings

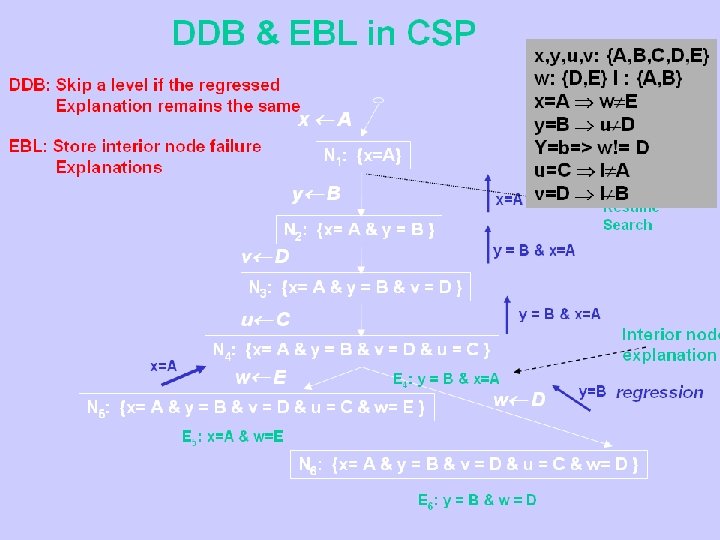
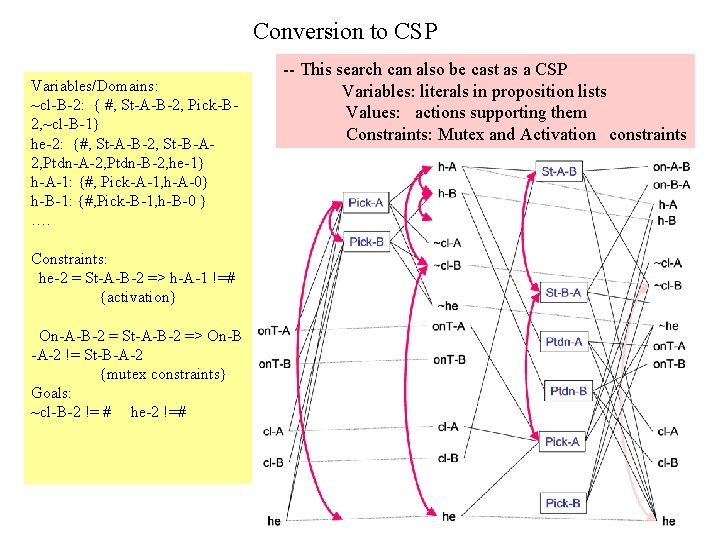
Conversion to CSP Variables/Domains: ~cl-B-2: { #, St-A-B-2, Pick-B 2, ~cl-B-1} he-2: {#, St-A-B-2, St-B-A 2, Ptdn-A-2, Ptdn-B-2, he-1} h-A-1: {#, Pick-A-1, h-A-0} h-B-1: {#, Pick-B-1, h-B-0 } …. Constraints: he-2 = St-A-B-2 => h-A-1 !=# {activation} On-A-B-2 = St-A-B-2 => On-B -A-2 != St-B-A-2 {mutex constraints} Goals: ~cl-B-2 != # he-2 !=# -- This search can also be cast as a CSP Variables: literals in proposition lists Values: actions supporting them Constraints: Mutex and Activation constraints

Why is Memoization such a neat idea for Graphplan? ?

Mutex propagation as CSP pre-processing • Suppose we start with a PG that only marks every pair of “interfering” actions as mutex • Any pair of non-noop actions are interfering • Any pair of actions are interfering if one gives P and other gives or requires ~P • No propagation is done – Converting this PG and CSP and solving it will still give a valid solution (if there is one) – So what is mutex propagation doing? • It is “explicating” implicit constraints • A special subset of “ 3 -consistency” enforcement – Recall that enforcing k-consistency involves adding (k-1)-ary constraints – *Not* full 3 -consistency (which can be much costlier) » So enforcing the consistency on PG is cheaper than enforcing it after conversion to CSP. . .

Alternative encodings. . • The problem of finding a valid plan from the planning graph can be encoded on any combinatorial substrate • Alternatives: – CSP [GP-CSP] – SAT [Blackbox; SATPLAN] – IP [Vossen et. Al]

a 00 , ti 20 mp a h b [Do am K & ] Compilation to CSP Goals: In(A), In(B) CSP: Given a set of discrete variables, the domains of the variables, and constraints on the specific values a set of variables can take in combination, FIND an assignment of values to all the variables which respects all constraints Constraints: Mutual exclusion ~[ ( In-A-1 = Load-A-1) & [Cor r regre esponds ssion to a -base d pr oof] Variables: Propositions (In-A-1, In-B-1, . . At-R-E-0 …) Domains: Actions supporting that proposition in the plan In-A-1 : { Load-A-1, #} At-R-E-1: {P-At-R-E-1, #} (At-R-M-1 = Fly-R-1)] ; etc. . Activation In-A-1 != # & In-B-1 != # (Goals must have action assignments) In-A-1 = Load-A-1 => At-R-E-0 != # , At-A-E-0 != # (subgoal activation constraints)

tz & u a [K an] m l e S Compilation to SAT Goals: In(A), In(B) SAT is CSP with Boolean Variables Init: At-R-E-0 & At-A-E-0 & At-B-E-0 Goal: In-A-1 & In-B-1 Graph: “cond at k => one of the supporting actions at k-1” In-A-1 => Load-A-1 In-B-1 => Load-B-1 At-R-M-1 => Fly-R-1 At-R-E-1 => P-At-R-E-1 Load-A-1 => At-R-E-0 & At-A-E-0 Load-B-1 => At-R-E-0 & At-B-E-0 P-At-R-E-1 => At-R-E-0 h ~In-A-1 V ~ At-R-M-1 “Actions => preconds” ~In-B-1 V ~At-R-M-1 “Mutexes”

Blackbox • Blackbox solves planning problems by converting them into SAT. – Very fast – Tried different solvers • Local search (GSAT) • Systematic search with EBL (Rel. SAT) • In 2000, GP-CSP could beat Blackbox – But in 2001, a newer “SUPER-DUPER” SAT solver called CHAFF was developed, that significantly speeds up Graphplan » By folks in CAD community (EE folks—see getting other people to do our work) – Currently, CSP people are trying to copy over the ideas from CHAFF to CSP.

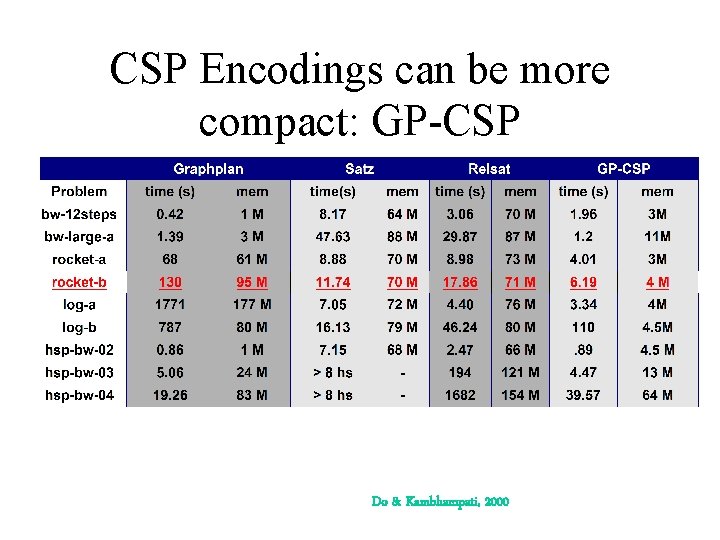
CSP Encodings can be more compact: GP-CSP Do & Kambhampati, 2000

Compilation to Integer Linear Programming ILP: Given a set of real valued variables, a linear objective function on the variables, a set of linear inequalities on the variables, and a set of integrality restrictions on the variables, Find the values of the feasible variables for which the objective function attains the maximum value -- 0/1 integer programming corresponds closely to SAT problem • Motivations – Ability to handle numeric quantities, and do optimization – Heuristic value of the LP relaxation of ILP problems • Conversion – Convert a SAT/CSP encoding to ILP inequalities • E. g. X v ~Y v Z => x + (1 - y) + z >= 1 – Explicitly set up tighter ILP constraints) autz; K er & l; us] inequalities [(Cutting s l o l a o W et. a op m i n D e Voss mayr & Bock

Vossen/Ball/Lotem/Nau work • Vossen et. Al. [IJCAI 99] tried two different IP encodings – First one is the simple conversion of a planning graph SAT encoding to IP (see previous slide) – The second encoding used two ideas • Compile away proposition variables. – The change of truth value of a proposition is equated to the occurrence of one of the actions that can give that proposition. This is basically a known transformation—see the Mc. Allester/Kautz/Selman paper. (see next slide) • Reformulate the constraints to make better use of expressiveness provided by IP – E. g. IP is particularly good at compactly encoding n-ary mutex constraints—even for n>2 – To say only one of X 1. . Xn can be true, we just say X 1+X 2+…Xn <= 1 – In SAT, we have to write n constraints of the form » Xi => ~X 1, ~X 2…~Xi-1, ~Xi+1, …. ~Xn – (IP, on the other hand, will have harder time representing “All-different” constraints)

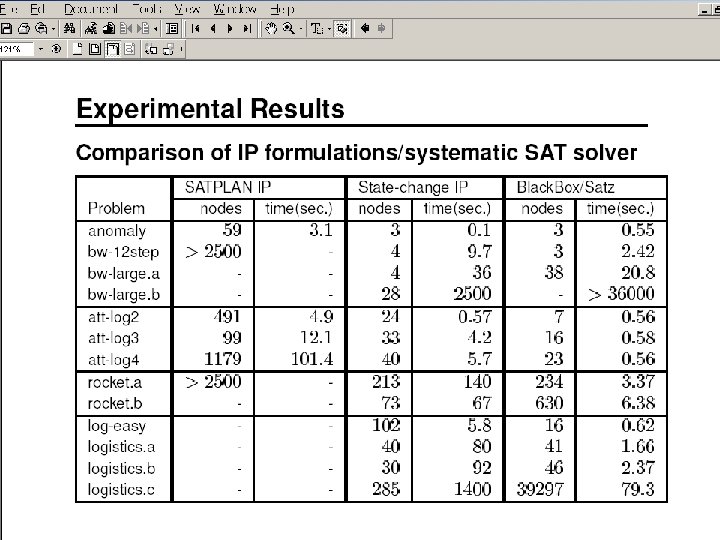
Empirical performance of IP Encodings • As seen in the previous slide, IP encodings are not competitive with SAT/CSP encodings for classical planning • Not surprising because we are neither exercizing the “optimizing” properties of IP, nor are we exercizing its ability to encode numerical variables – IP may well do better if we are interested in finding “cost-optimal” plans of a given makespan (length) • No one has confirmed this as yet… – IP encodings may well be more useful when we have numerical quantities such as actions consuming metric resources (preconditions and effects involve numbers) • See the work by Kautz and Walser(AAAI-99) or LPSat (Wolfman/Weld—IJCAI 99).

Relative Tradeoffs Offered by the various compilation substrates • CSP encodings support implicit representations – More compact encodings [Do & Kambhampati, 2000] – Easier integration with Scheduling techniques • ILP encodings support numeric quantities – Seamless integration of numeric resource constraints [Walser & Kautz, 1999] – Not competitive with CSP/SAT for problems without numeric constraints • SAT encodings support axioms in propositional logic form – May be more natural to add (for whom ; -) – Very active research on finding faster solvers. . • Davis Putnam ( Satz; Rel. Sat; Chaff) • Gsat

Direct vs. compiled solution extraction DIRECT 8 Need to adapt CSP/SAT techniques 4 Can exploit approaches for compacting the plan 4 Can make the search incremental across iterations Compiled 4 Can exploit the latest advances in SAT/CSP solvers 8 Compilation stage can be time consuming, leads to memory blow-up 8 Makes it harder to exploit search from previous iterations 4 Makes it easier to add declarative control knowledge

LPG: Local Search on Planning Graphs • The winner of the 2003 planning competition was “LPG” – LPG does local search on the planning graphs directly (rather than, say, convert to SAT and use GSAT/Walk. SAT). • Select a seed subgraph of a k-length graph • If it is solution; you are done. • If not “Repair” it – Repairs include adding/deleting action/precondition nodes – + expanding the planning graph – Repair techniques tend to be more tuned to planning graphs, and are thus more effective in solving planning problems. [A short paper is in AIPS 2002. http: //prometeo. ing. unibs. it/lpg]

But why go from Planning Graph to CSP/SAT/ILP? Why not directly make those encodings? What—if any thing is Planning Graph Buying us?

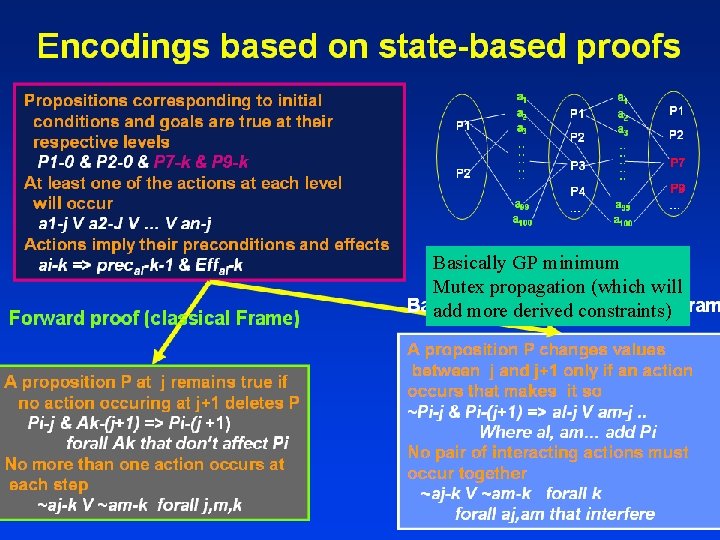
Basically GP minimum Mutex propagation (which will add more derived constraints)

Should we bother with Proof-based encodings? • Clearly Graphplan-based encodings are better than backward-proof based encodings – Because Graphplan does Mutex propagation – And mutex propagation is harder to do on direct SAT • And yet, it is useful to know how to set up encodings directly—since if we don’t know how to do directed consistency enforcement, then we at least know how to solve the problem – Particularly useful for non-classical problems, where we haven’t yet found really effective mutex propagation procedures. – If “neural networks are often the second best way of solving any problem”, you can say that direct SAT(or other) encodings are the second best way of solving planning problems • Which is better than “no way at all”