The role of phase transformation kinetics in phase

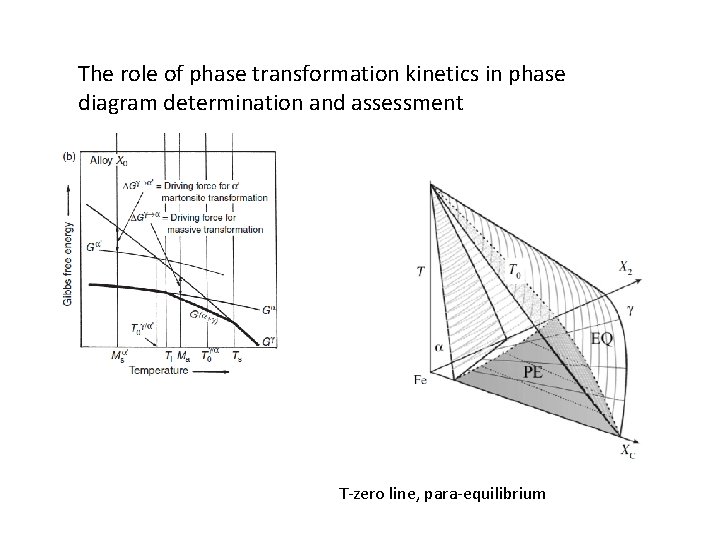
The role of phase transformation kinetics in phase diagram determination and assessment T-zero line, para-equilibrium

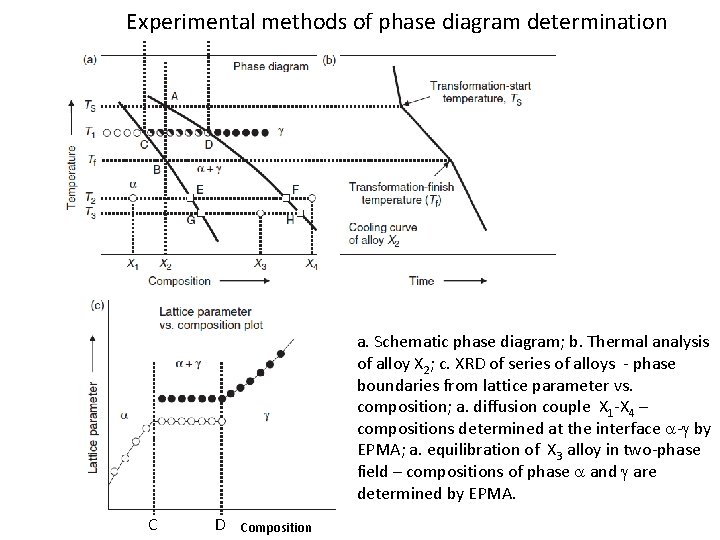
Experimental methods of phase diagram determination a. Schematic phase diagram; b. Thermal analysis of alloy X 2; c. XRD of series of alloys - phase boundaries from lattice parameter vs. composition; a. diffusion couple X 1 -X 4 – compositions determined at the interface a-g by EPMA; a. equilibration of X 3 alloy in two-phase field – compositions of phase a and g are determined by EPMA. C D Composition

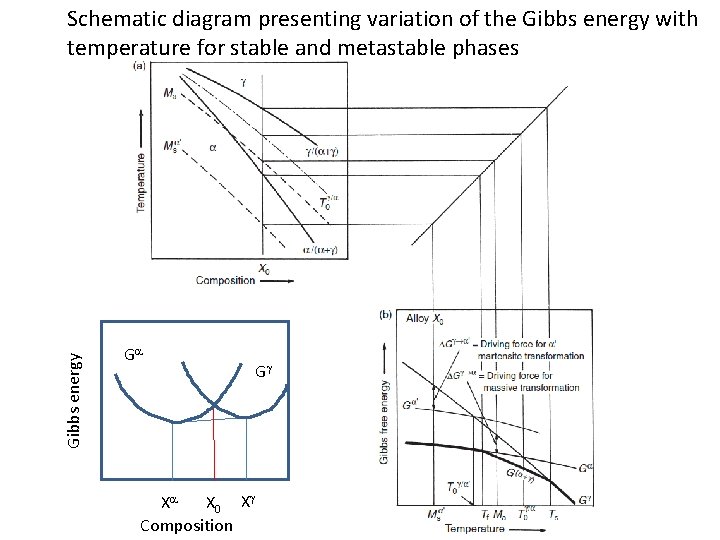
Gibbs energy Schematic diagram presenting variation of the Gibbs energy with temperature for stable and metastable phases Ga Gg G Xa X 0 Xg Composition

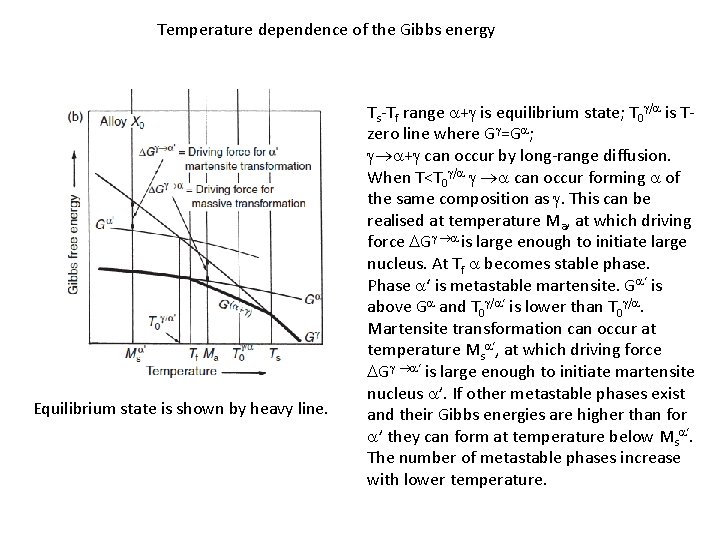
Temperature dependence of the Gibbs energy Equilibrium state is shown by heavy line. Ts-Tf range a+g is equilibrium state; T 0 g/a is Tzero line where Gg=Ga; g a+g can occur by long-range diffusion. When T<T 0 g/a g a can occur forming a of the same composition as g. This can be realised at temperature Ma, at which driving force DGg a is large enough to initiate large nucleus. At Tf a becomes stable phase. Phase a‘ is metastable martensite. Ga‘ is above Ga and T 0 g/a‘ is lower than T 0 g/a. Martensite transformation can occur at temperature Msa‘, at which driving force DGg a‘ is large enough to initiate martensite nucleus a’. If other metastable phases exist and their Gibbs energies are higher than for a’ they can form at temperature below Msa‘. The number of metastable phases increase with lower temperature.

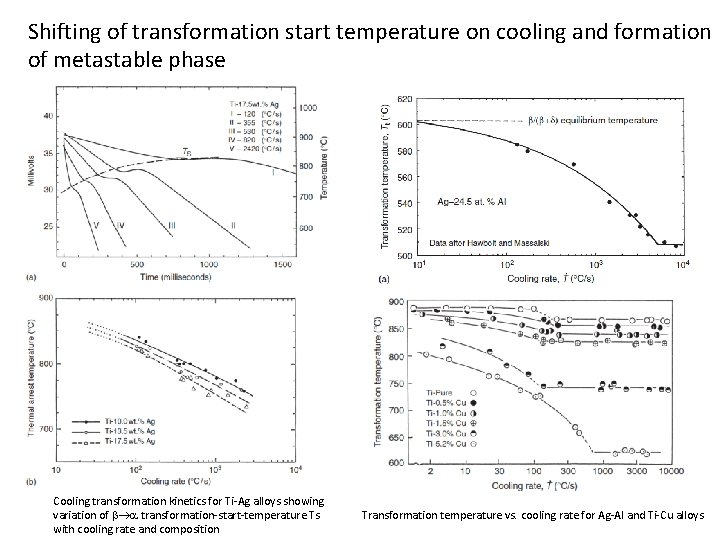
Shifting of transformation start temperature on cooling and formation of metastable phase Cooling transformation kinetics for Ti-Ag alloys showing variation of b a transformation-start-temperature Ts with cooling rate and composition Transformation temperature vs. cooling rate for Ag-Al and Ti-Cu alloys

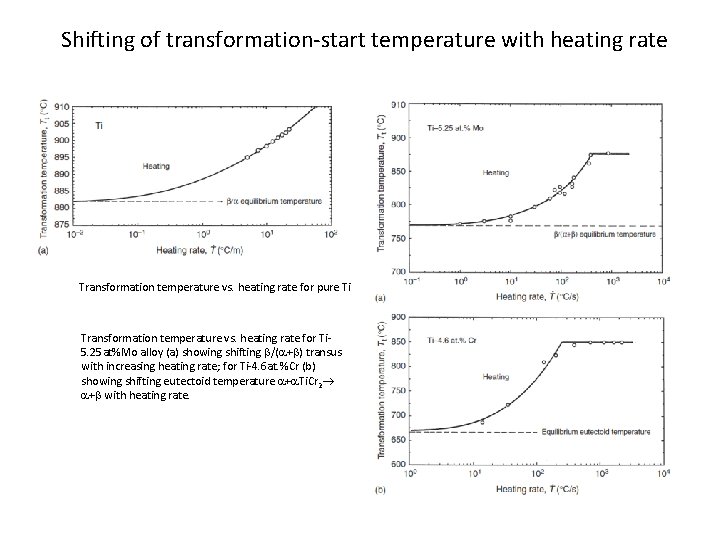
Shifting of transformation-start temperature with heating rate Transformation temperature vs. heating rate for pure Ti Transformation temperature vs. heating rate for Ti 5. 25 at%Mo alloy (a) showing shifting b/(a+b) transus with increasing heating rate; for Ti-4. 6 at. %Cr (b) showing shifting eutectoid temperature a+a. Ti. Cr 2 a+b with heating rate.

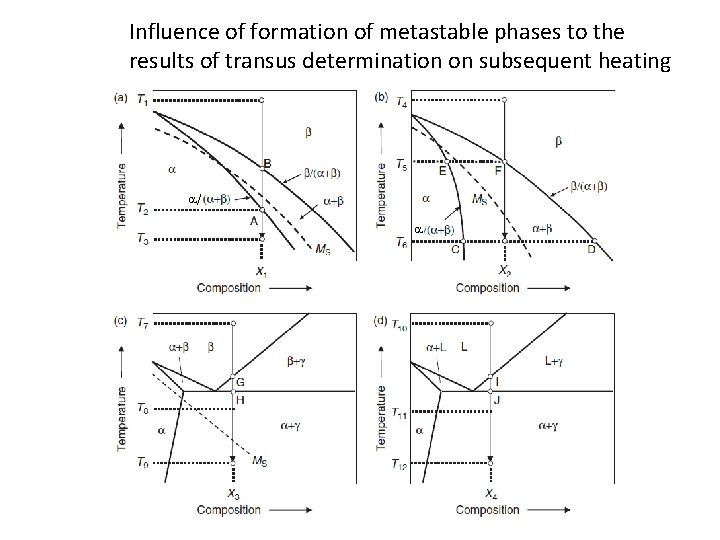
Influence of formation of metastable phases to the results of transus determination on subsequent heating a/ a

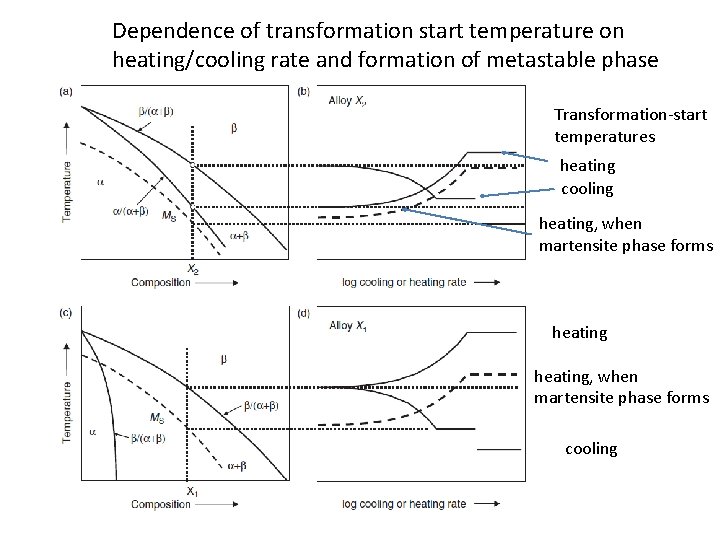
Dependence of transformation start temperature on heating/cooling rate and formation of metastable phase Transformation-start temperatures heating cooling heating, when martensite phase forms cooling

Example: Fe-Ni system The heating transformation start temperature (As) should be above g/(a+g) transus because heating always shift phase boundary to higher temperature. The fact that As on heating is below the transus indicates that metastable structure has been produced during the cooling. The As is temperature of metastable phase transformation to g phase and has no direct relation to equilibrium transus. Comparison of cooling and heating transformation start temperatures with equilibrium g/(a+g) transus in Fe-Ni system

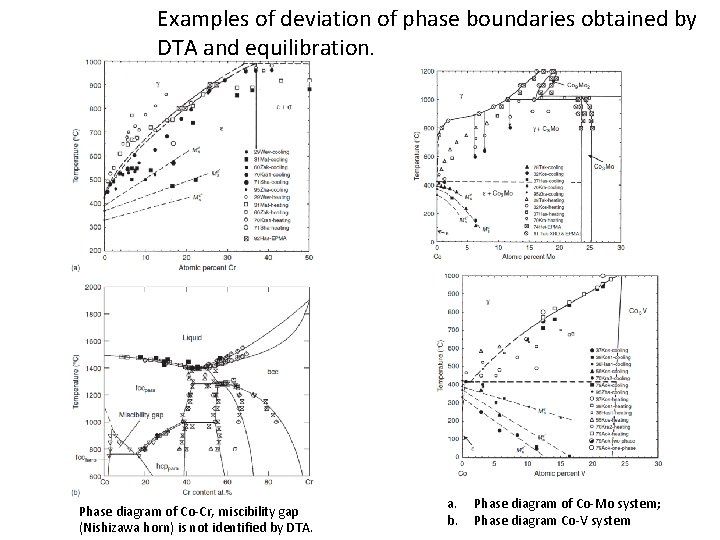
Examples of deviation of phase boundaries obtained by DTA and equilibration. Phase diagram of Co-Cr, miscibility gap (Nishizawa horn) is not identified by DTA. a. b. Phase diagram of Co-Mo system; Phase diagram Co-V system

Concluding remarks The specific high cooling and heating rate that cause significant deviation from equilibrium depends on the alloy, its composition, grain size, phase structure and temperature of the transus (relative to solidus). If high temperature phase is liquid the shifting of temperature during slow cooling and heating rate is less pronounced that for solid-solid transformation, because it is easier to nucleate critical nucleus from liquid than from solid phase. DTA data for transformations including liquid are more reliable than for solid-solid transformation. For high Fe-Ni alloys even few degree per minute is high cooling rate because diffusion is difficult. It is recommended to use the results of equilibrated alloys or diffusion couple to assess phase boundaries. It should be mentioned that transformation-finish temperature for cooling and heating (Mf, Af) has very little connection with equilibrium transus, because transformation start temperatures are already shifted away from equilibrium. If transformation temperature is below half of the homologous melting point, one need to pay special attention to potential problem associated with kinetics of phase transformation and shifting transformation temperature away from equilibrium phase boundaries.

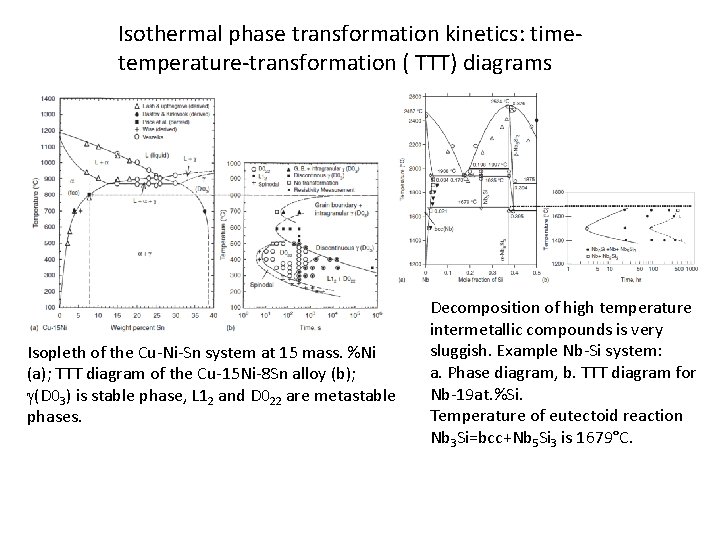
Isothermal phase transformation kinetics: timetemperature-transformation ( TTT) diagrams Isopleth of the Cu-Ni-Sn system at 15 mass. %Ni (a); TTT diagram of the Cu-15 Ni-8 Sn alloy (b); g(D 03) is stable phase, L 12 and D 022 are metastable phases. Decomposition of high temperature intermetallic compounds is very sluggish. Example Nb-Si system: a. Phase diagram, b. TTT diagram for Nb-19 at. %Si. Temperature of eutectoid reaction Nb 3 Si=bcc+Nb 5 Si 3 is 1679°C.

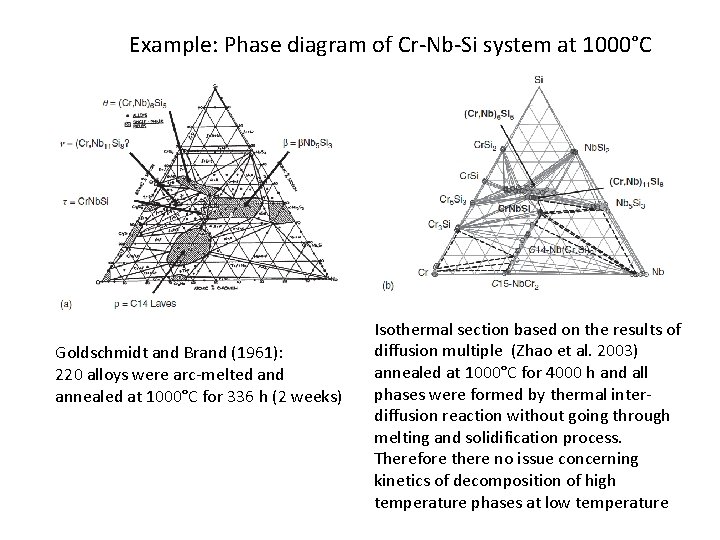
Example: Phase diagram of Cr-Nb-Si system at 1000°C Goldschmidt and Brand (1961): 220 alloys were arc-melted annealed at 1000°C for 336 h (2 weeks) Isothermal section based on the results of diffusion multiple (Zhao et al. 2003) annealed at 1000°C for 4000 h and all phases were formed by thermal interdiffusion reaction without going through melting and solidification process. Therefore there no issue concerning kinetics of decomposition of high temperature phases at low temperature

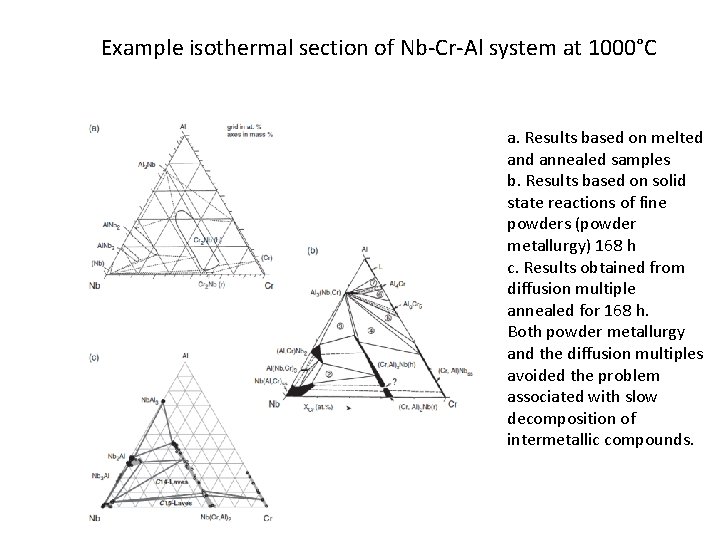
Example isothermal section of Nb-Cr-Al system at 1000°C a. Results based on melted annealed samples b. Results based on solid state reactions of fine powders (powder metallurgy) 168 h c. Results obtained from diffusion multiple annealed for 168 h. Both powder metallurgy and the diffusion multiples avoided the problem associated with slow decomposition of intermetallic compounds.

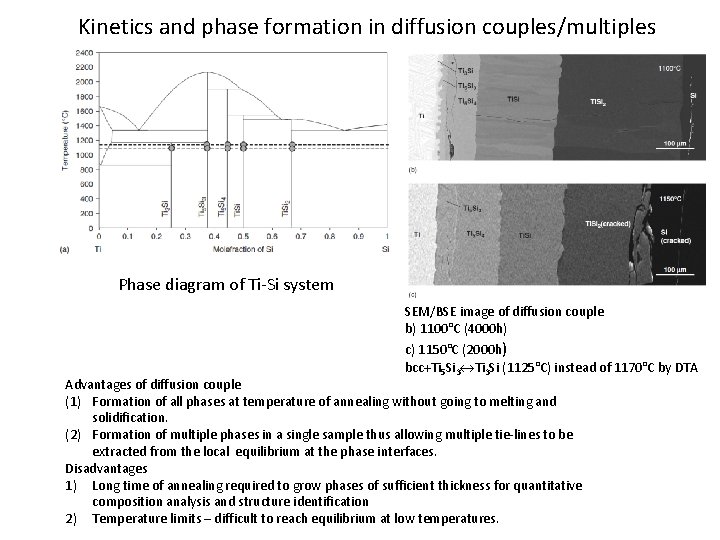
Kinetics and phase formation in diffusion couples/multiples Phase diagram of Ti-Si system SEM/BSE image of diffusion couple b) 1100°C (4000 h) c) 1150°C (2000 h) bcc+Ti 5 Si 3 Ti 3 Si (1125°C) instead of 1170°C by DTA Advantages of diffusion couple (1) Formation of all phases at temperature of annealing without going to melting and solidification. (2) Formation of multiple phases in a single sample thus allowing multiple tie-lines to be extracted from the local equilibrium at the phase interfaces. Disadvantages 1) Long time of annealing required to grow phases of sufficient thickness for quantitative composition analysis and structure identification 2) Temperature limits – difficult to reach equilibrium at low temperatures.

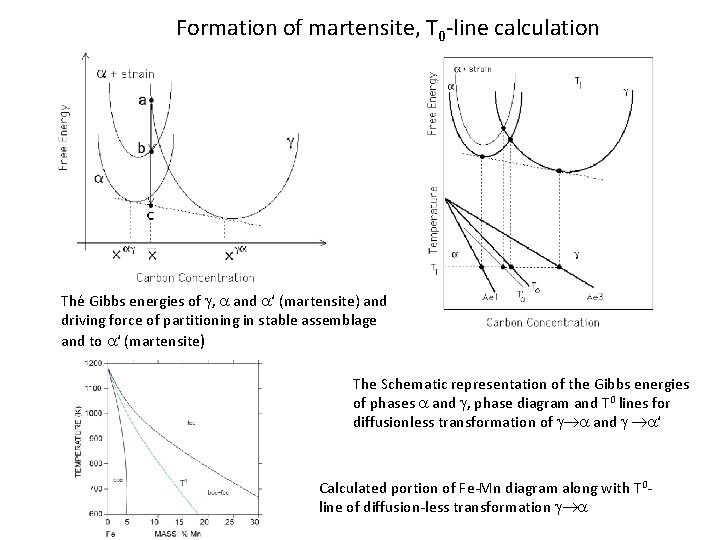
Formation of martensite, T 0 -line calculation Thé Gibbs energies of g, a and a‘ (martensite) and driving force of partitioning in stable assemblage and to a‘ (martensite) The Schematic representation of the Gibbs energies of phases a and g, phase diagram and T 0 lines for diffusionless transformation of g a and g a‘ Calculated portion of Fe-Mn diagram along with T 0 line of diffusion-less transformation g a

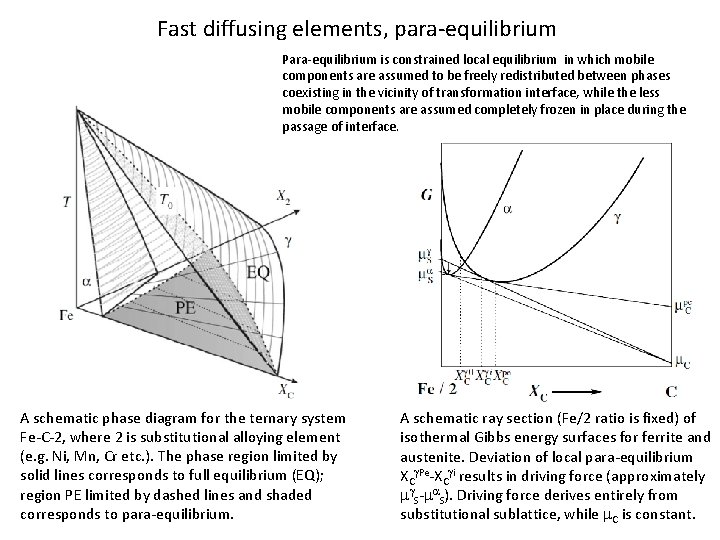
Fast diffusing elements, para-equilibrium Para-equilibrium is constrained local equilibrium in which mobile components are assumed to be freely redistributed between phases coexisting in the vicinity of transformation interface, while the less mobile components are assumed completely frozen in place during the passage of interface. A schematic phase diagram for the ternary system Fe-C-2, where 2 is substitutional alloying element (e. g. Ni, Mn, Cr etc. ). The phase region limited by solid lines corresponds to full equilibrium (EQ); region PE limited by dashed lines and shaded corresponds to para-equilibrium. A schematic ray section (Fe/2 ratio is fixed) of isothermal Gibbs energy surfaces for ferrite and austenite. Deviation of local para-equilibrium XCg. Pe-XCgi results in driving force (approximately mg. S-ma. S). Driving force derives entirely from substitutional sublattice, while m. C is constant.

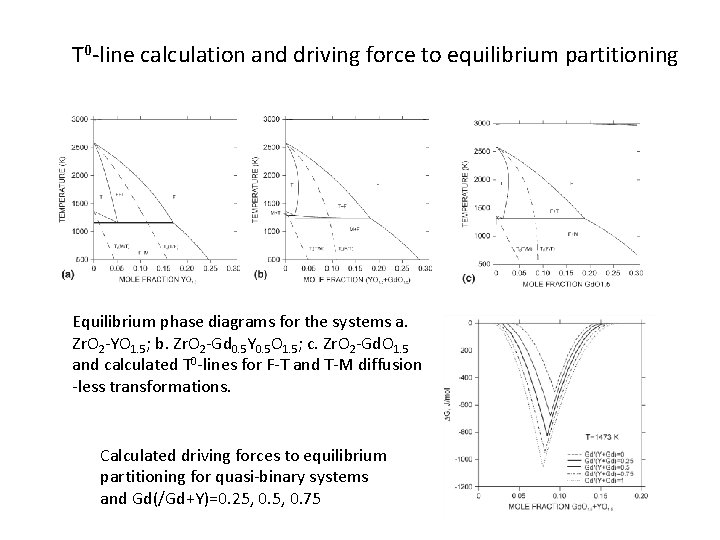
T 0 -line calculation and driving force to equilibrium partitioning Equilibrium phase diagrams for the systems a. Zr. O 2 -YO 1. 5; b. Zr. O 2 -Gd 0. 5 Y 0. 5 O 1. 5; c. Zr. O 2 -Gd. O 1. 5 and calculated T 0 -lines for F-T and T-M diffusion -less transformations. Calculated driving forces to equilibrium partitioning for quasi-binary systems and Gd(/Gd+Y)=0. 25, 0. 75

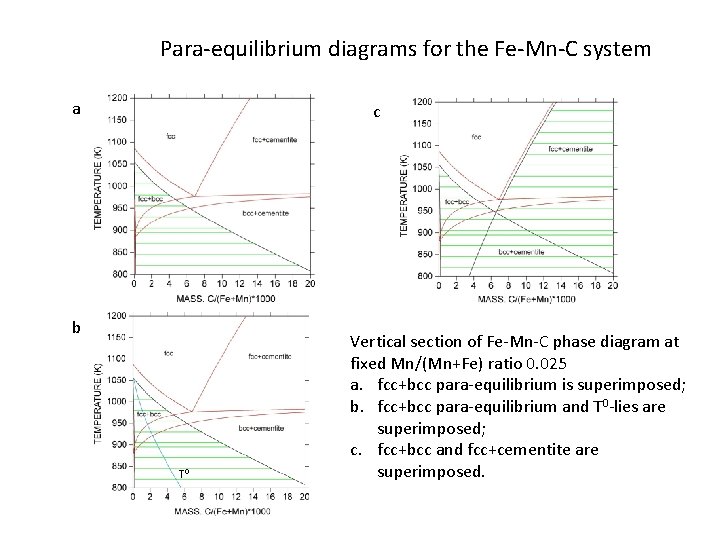
Para-equilibrium diagrams for the Fe-Mn-C system a c b T 0 Vertical section of Fe-Mn-C phase diagram at fixed Mn/(Mn+Fe) ratio 0. 025 a. fcc+bcc para-equilibrium is superimposed; b. fcc+bcc para-equilibrium and T 0 -lies are superimposed; c. fcc+bcc and fcc+cementite are superimposed.

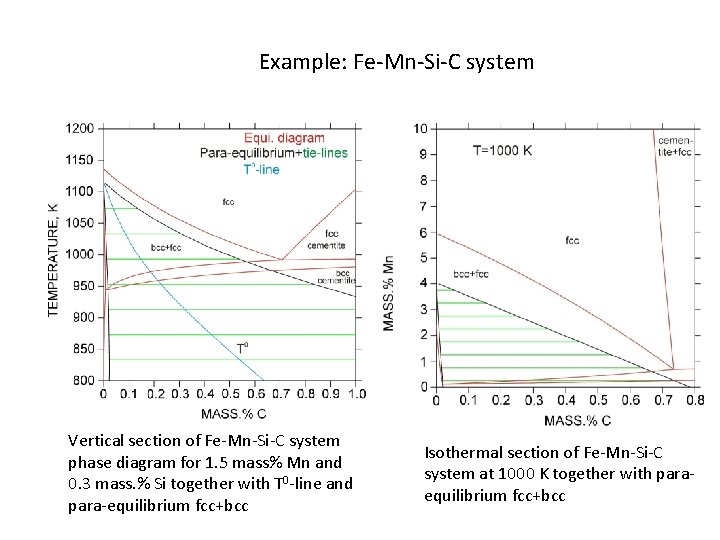
Example: Fe-Mn-Si-C system Vertical section of Fe-Mn-Si-C system phase diagram for 1. 5 mass% Mn and 0. 3 mass. % Si together with T 0 -line and para-equilibrium fcc+bcc Isothermal section of Fe-Mn-Si-C system at 1000 K together with paraequilibrium fcc+bcc

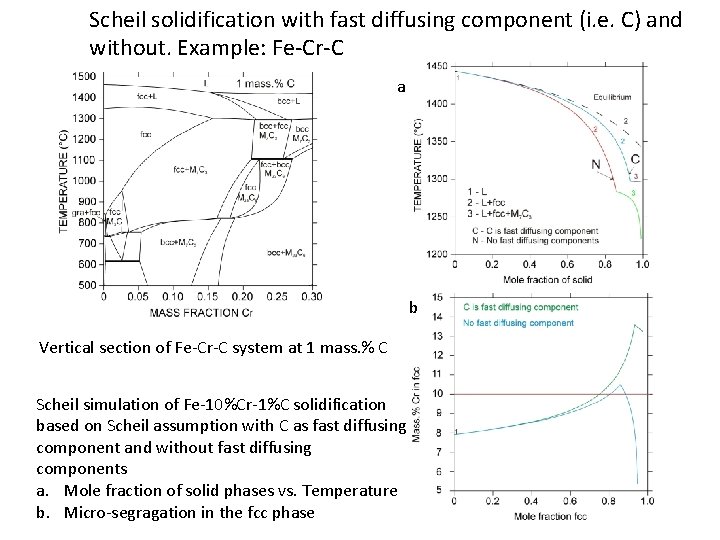
Scheil solidification with fast diffusing component (i. e. C) and without. Example: Fe-Cr-C a b Vertical section of Fe-Cr-C system at 1 mass. % C Scheil simulation of Fe-10%Cr-1%C solidification based on Scheil assumption with C as fast diffusing component and without fast diffusing components a. Mole fraction of solid phases vs. Temperature b. Micro-segragation in the fcc phase