THE ROLE OF HYPOTHESIS TESTING IN MEDICAL RESEARCH

THE ROLE OF HYPOTHESIS TESTING IN MEDICAL RESEARCH Susan Ellenberg, Ph. D. Perelman School of Medicine University of Pennsylvania CRi. SM Workshop on Contemporary Issues in Hypothesis Testing University of Warwick September 16, 2016

YEAS AND NAYS FOR HYPOTHESIS TESTING w Hypothesis testing has been well established in medical research for many decades, but not without pushback w In 1990, Ken Rothman founded the journal Epidemiology, and banned p-values (but not confidence intervals) from journal papers w More recently, a psychology journal has banned all statistical inferential procedures, urging authors to do a more thoughtful job in reporting descriptive statistics w Why do we do it, and why are there hypothesis testing haters? 2

INTERPRETATION OF MEDICAL DATA w Physicians want to identify improved ways to treat and prevent disease w Improved outcomes observed with a new treatment in a new cohort of patients, whether compared to historical data or to a concurrent control group, can be hard to interpret ― Intuitive recognition of the play of chance, versus the desire to believe we have found a better treatment ― How much better do the outcomes have to be before we should believe it? 3

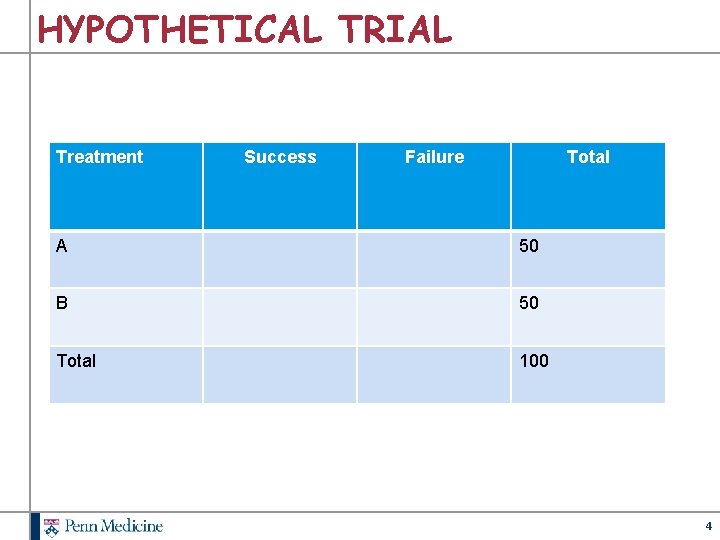
HYPOTHETICAL TRIAL Treatment Success Failure Total A 50 B 50 Total 100 4

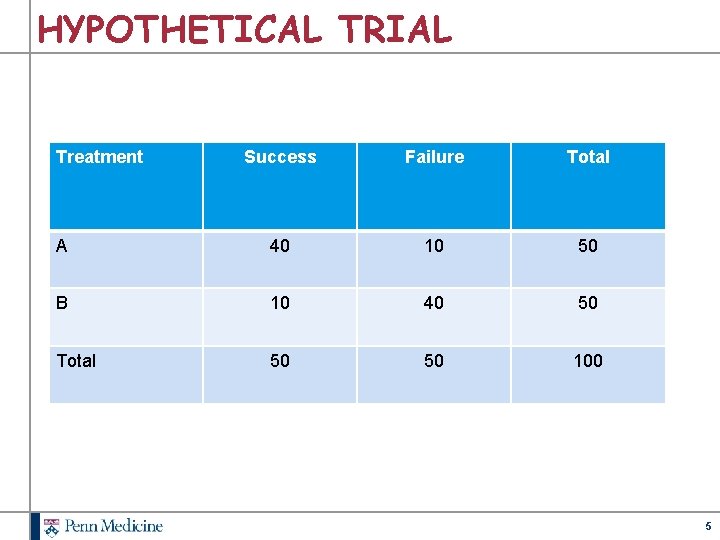
HYPOTHETICAL TRIAL Treatment Success Failure Total A 40 10 50 B 10 40 50 Total 50 50 100 5

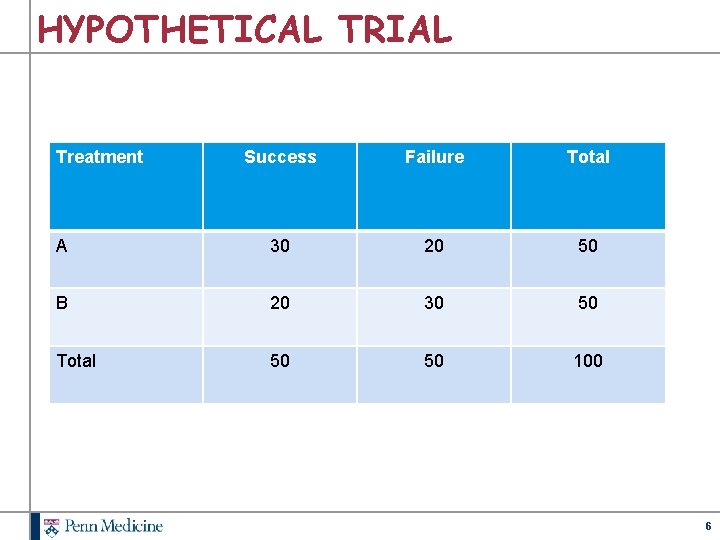
HYPOTHETICAL TRIAL Treatment Success Failure Total A 30 20 50 B 20 30 50 Total 50 50 100 6

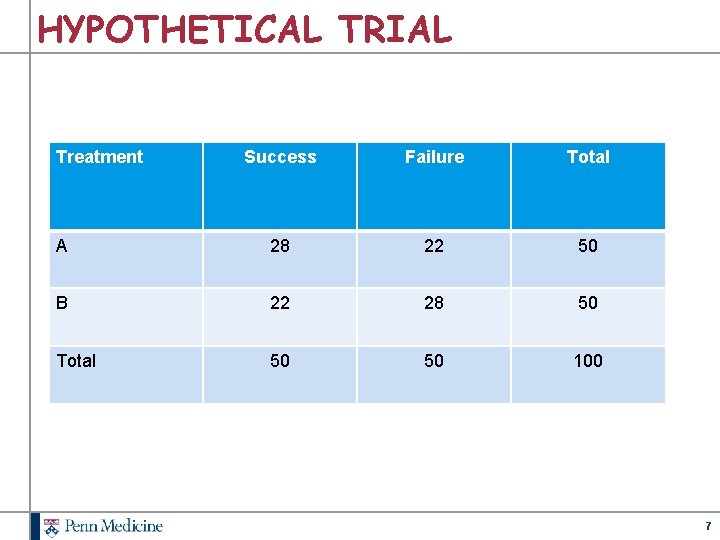
HYPOTHETICAL TRIAL Treatment Success Failure Total A 28 22 50 B 22 28 50 Total 50 50 100 7

HYPOTHESIS TESTING IN CLINICAL TRIALS w Some way was needed to determine how likely an observed difference was from random fluctuation w One obvious way: analogy to coin flips ― If you flip a coin 50 times and get heads 40 times, you are pretty sure it’s not a fair coin ― Easy to calculate how likely it would be to get 40 heads in 50 flips if it were a fair coin ― Natural way to look at the problem ― No need for a prior probability or use of calculus! 8

HYPOTHESIS TESTING IN CLINICAL TRIALS w Hypothesis testing is standard practice in clinical trials w Forms the basis for sample size considerations w Expected part of analytical plans w Relied on by journal editors and regulatory authorities w Medical interventions shown effective by these tests have clearly demonstrated improvements in public health w So—why has it become so controversial? 9

REASONS FOR CONTROVERSY 1. Hypothesis tests have been interpreted as absolute arbiters of truth, rather than as what they are: tools to help us make our best guesses at truth 10

ARBITER OF TRUTH w Not exactly what early proponents of hypothesis testing had in mind w Natural evolution for decision-makers ― Simplifies processes ― Cutoff for further consideration ― Reduction in perception of subjectivity w Provides guidance for experimenters ― Basis for sample size determination 11

EXAMPLE: DRUG REGULATION w U. S. Food and Drug Administration (FDA) often accused of over-focus on p-values w FDA typically requires 2 studies each showing a statistically significant benefit using a one-sided 0. 025 level test w Much concern about precedent and fairness in regulatory sphere—absolute standards help to counter view that some companies are treated more leniently than others w Still, flexibility frequently exercised 12

REASONS FOR CONTROVERSY 1. Hypothesis tests have been interpreted as absolute arbiters of truth, rather than as what they are: tools to help us make our best guesses at truth 2. Hypothesis tests don’t formally account for lots of information relevant to decisionmaking 13

ACCOUNTING FOR OTHER INFORMATION w There is always important prior information to take into account w In drug development, multiple considerations ― Biological plausibility ― Results of preliminary studies ― Results of studies of related drugs w Bayesian approaches incorporate such information into the analytical model w Frequentists use this information informally in interpreting study results w Additionally, quality of study conduct—potential for biased results 14

REASONS FOR CONTROVERSY 1. Hypothesis tests have been interpreted as absolute arbiters of truth, rather than as what they are: tools to help us make our best guesses at truth 2. Hypothesis tests don’t formally account for lots of information external to the experiment that are relevant to decisionmaking 3. Hypothesis tests don’t allow us to say how likely something is to be true, which is what most people want to say 15

INTERPRETATION OF RESULTS w A hypothesis test tells us how likely our result would be if there were no association between the intervention and the outcome w What many people want to know is how likely it is that an apparent association is real w When we say, “how likely is it that we would get 15 heads in 20 flips if we’re flipping a fair coin? ” no one seems to have a problem with that. w When we say, “how likely is it that we would see one drug looking so much better than another if they really had the same effect, ” that confuses people. 16

COIN FLIPS VS CLINICAL TRIALS w Key difference w When we flip coins, we expect the coin to be fair—the null hypothesis is what we believe to be true ― We will believe the coin is fair unless there is strong evidence to the contrary w When we do a clinical trial, we expect (or at least hope) that the null hypothesis is false ― At the outset, no strong basis to believe that the null hypothesis is true 17

REASONS FOR CONTROVERSY 1. Hypothesis tests have been interpreted as absolute arbiters of truth, rather than as what they are: tools to help us make our best guesses at truth 2. Hypothesis tests don’t formally account for lots of information external to the experiment that are relevant to decisionmaking 3. Hypothesis tests don’t allow us to say how likely something is to be true, which is what most people want to say 4. Results of hypothesis tests tell us nothing about the importance of the result 18

THE NULL HYPOTHESIS IS NEVER TRUE w If a study is large enough, the null hypothesis will be rejected with probability 1 w If a study is REALLY large, the null hypothesis may be rejected with a REALLY small p-value w Such a result does not help us understand anything about the problem we are studying w Typically not a problem in clinical research— resources do not permit huge studies that might detect small differences of no clinical importance w Bigger problem—finding resources to do a study large enough to detect a clinically important effect 19

ONE MORE ISSUE w P-values that typically must be achieved to declare “statistical significance” are totally arbitrary w We use 0. 05 because that’s what R. A. Fisher tabulated 20

THAT’S TRUE! w Alpha levels of 0. 05 and 0. 01 are completely arbitrary w However, it would be hopelessly inefficient in many spheres not to have some arbitrary benchmarks to guide decision-making w These cutoffs shouldn’t rigidly determine decision, but they are useful in determining which possibilities merit careful consideration 21

STATEMENT ON P-VALUES w The American Statistical Association convened about 30 leading statisticians to draft a statement about statistical significance and pvalues w Document offers 6 principles that address misconceptions and misuse of p-values, and elaborates on each w Not a consensus statement—but close w Published in The American Statistician earlier this year (Wasserstein and Lazar, The American Statistician 70: 129 -33, 2016) w Supplemental material includes comments from other statisticians 22

SIX PRINCIPLES w P-values can indicate how incompatible the data are with a specified statistical model. w P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone. w Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold. w Proper inference requires full reporting and transparency. w A p-value, or statistical significance, does not measure the size of an effect or the importance of a result. w By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis. 23

CONCLUDING REMARKS w Hypothesis tests and associated significance tests are useful tools for decision-makers w They are certainly not the only useful tools w Most statisticians, even those with a Bayesian bent, believe that hypothesis testing can be useful if the results are interpreted properly w Appropriate application and interpretation of hypothesis testing can support evidence-based decision making w The position that research results can be reliably assessed without statistical tools to quantitate uncertainty is untenable 24