The Resolution of Small Angle Neutron Scattering SANS

The Resolution of Small Angle Neutron Scattering (SANS): Theory and the Experimental Authors: • E. L. Maweza (University of Fort Hare in SA) • A. KUKLIN (Supervisor: JINR in Dubna)

Table of Contents 1. 2. 3. 4. 5. 6. 7. 8. 9. Introduction Theory and Literature Review Experimental Setup Description of the Equipment Sample Characterization Experimental Procedure Results and discussion Conclusion Acknowledgements

Introduction • The choice of Small Angle Neutron Scattering (SANS) as a technique to investigate the structure of materials was based at its efficiency in determining their structural properties at length range 10 to 1000 Å. • The SANS experiments require a wide range of momentum transfer (Q range) to determine reliable structural properties of materials. • Frank’s Laboratory for Neutron Physics currently uses a modernized two-detector (“old” and “new”) system in order to increase the Q-range of the instrument.

Theory and Literature Review • The intensity of the scattered neutron beam is given by – P(Q) : • Definition: – S( ) : Factor. • Definition: Periodicity function – Form factor. , where Inter-particle function - Structure and Figure: 1: Schematic representation of a scattering experiment.

Bragg’s equation for crystallite periodicity and size • Bragg’s Equation is given by • Combining the Bragg’s equation with momentum transfer we obtain the periodicity of the crystal. • The size of the crystallite is given by the De. Bye’s equation. • The wavelength of the neutrons is given by

Experimental Setup 1. The two-reflector system. 2. The reactor with the moderator. 3. The chopper. 4, 5. The first collimator. 6, 7. Vacuum cube. 8. The second collimator. 9, 11. Table for the sample holder , sample holder 10. The water bath thermostat 12, 14. Vanadium Standards 13. First detector 15, 16. Second detector 17. The direct neutron beam detector Figure 2: The two detector Yu. MO spectrometer http: //flnp. jinr. ru/135/

Description of the Equipment • The Yu. MO two-detector system uses 8 homemade ring wire detectors with central holes: – Old detector : 200 mm central hole. – New detector : 80 mm central hole. • SANS experiments are carried out in two stages. – The study of the sample in the beam without vanadium standards. – The sample with both vanadium standards in the beam.

Sample Characterization • The sample for this project is Silver Behenate powder (“Ag. BE”). – Chemical Formula: – Made up of small plate-like crystals – Surface dimensions: (0. 2 -2. 0 µm) and thickness ≤ 1000 Å • The long-period spacing obtained from literature is given by 58. 378 Å.

Experimental Procedure • The primary aim is to obtain periodicity and the size of the Ag. BE crystallite. • Origin data analysis program was used to treat the results obtained from the SANS program. • The data obtained analyzed covers the neutron scattering observed by detectors from the 2 nd to the 7 th ring. • The peaks occur where the diffraction of the Ag. BE crystals take place.

Results and Discussion Figure 3: Illustration of the periodicity of Ag. BE by Lorentz Approximation.

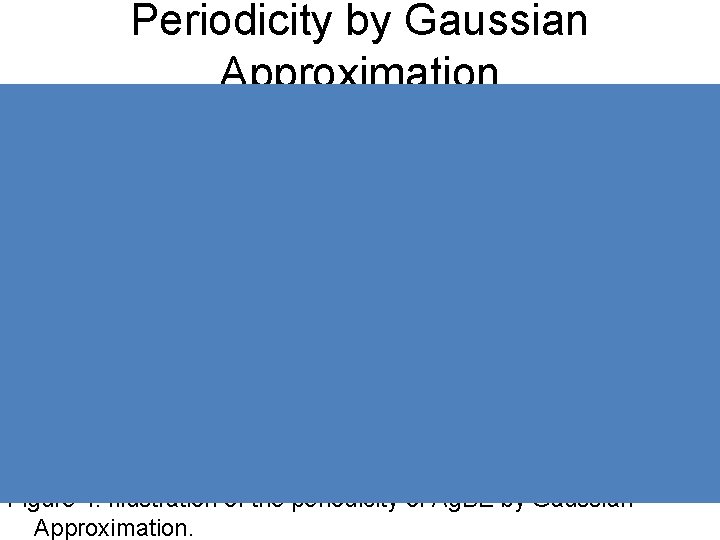
Periodicity by Gaussian Approximation Figure 4: Illustration of the periodicity of Ag. BE by Gaussian Approximation.

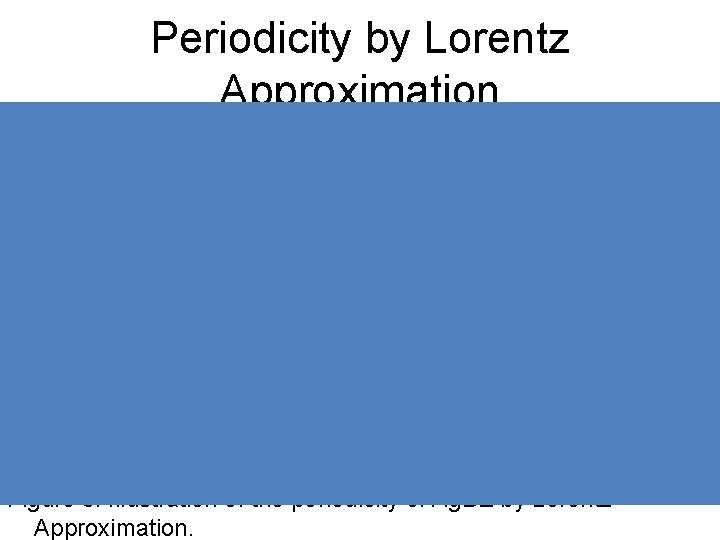
Periodicity by Lorentz Approximation Figure 5: Illustration of the periodicity of Ag. BE by Lorentz Approximation.

The size of the Ag. BE crystal Figure 6: Illustration of the size of Ag. BE crystallite.

Analysis • Periodicity values that are in agreement with values obtained by other authors were expected for Ag. BE because it has been adopted as calibration standard. • The considerable deviation that was observed is attributed to systematic errors like: – Time of delay must be calculated more precisely • (not by “vision” as we did. ) – Asymmetry of the peaks (as shown in figure 3). • The size of the crystallite clearly becomes constant for bigger rings showing better

Conclusion • The characteristic parameters of Ag. BE were obtained. – The periodicity ≤ 58 Å – The size of crystallite was about 7300 Å. . • It was shown, that time of delay obtained from raw spectra must be corrected. • In this case we have good agreement with another authors. • The Ag. BE is suitable as calibration sample.

Conclusion • Standard procedure of SAS program gives us the Gaussian resolution value. • Both the Gaussian and Lorentz distribution is suitable for low resolution of SANS method. • For averaging data using Gaussian distribution one should be careful.

References • Teixeira, J. (1992) “ Introduction to Small Angle Neutron Scattering Applied to Colloidal Science”. Structure and Dynamics of Strongly Interacting Colloids and Supramolecular Aggregates in Solution. Kluwer Academic Publishers. • Cser, L. (1976)”Investigation of Biological Macromolecular Systems With Pulsed Neutron Source- A Review”. Brookhaven. Symp. Biol. (27) VII 3 – VII 29. • Keiderling, U. , Gilles, R. , Wiedernmann, A. , (1999) “Application of Silver Behenate Powder for the Wavelength Calibration of a SANS instrument- a comprehensive study of experimental setup variations and data processing techniques”. J. Appl. Cryst. , 32. , 456 – 463. • A. J. Kuklin, A. KH. Islamov, V. I. , Gordelly (2005), Two-Detector System for Small-Angle Neutron Scattering Instrument. Neutron News. V. 16, 16 -18 pp

Acknowledgements 1. JINR SA Representation (Dr. Jacobs and Prof. Lekala) 2. Yu. MO Team i. iii. iv. v. Raul Erhan Oleksandr Ivankov Dmitry Soloviov Andrey Rogachev Yury Kovalev

Helpful definitions