The Rendering Equation Direct local illumination n Light

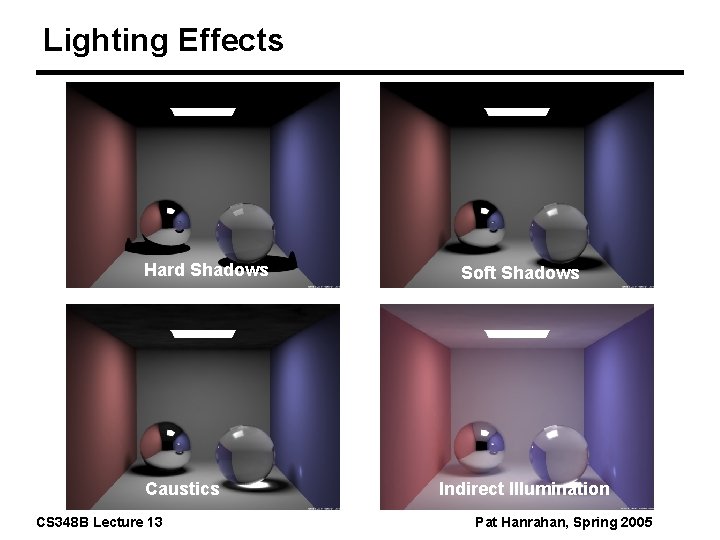
The Rendering Equation Direct (local) illumination n Light directly from light sources n No shadows Indirect (global) illumination n Hard and soft shadows n Diffuse interreflections (radiosity) n Glossy interreflections (caustics) CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Early Radiosity CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Lighting Effects Hard Shadows Caustics CS 348 B Lecture 13 Soft Shadows Indirect Illumination Pat Hanrahan, Spring 2005

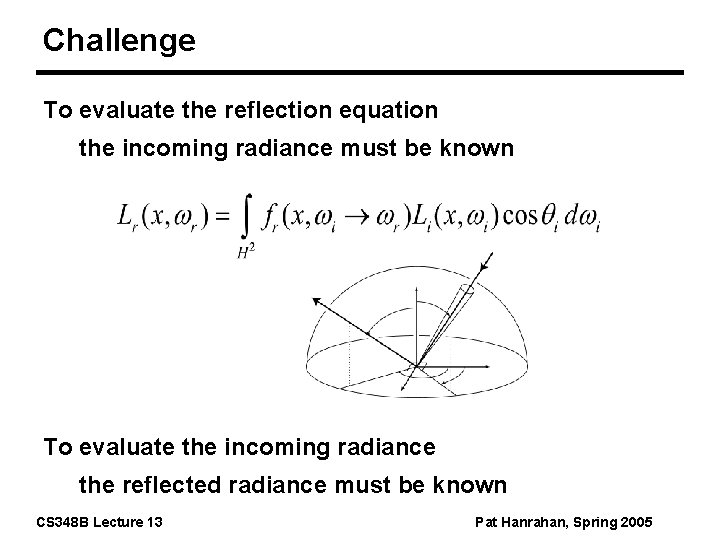
Challenge To evaluate the reflection equation the incoming radiance must be known To evaluate the incoming radiance the reflected radiance must be known CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

To The Rendering Equation Questions 1. How is light measured? 2. How is the spatial distribution of light energy described? 3. How is reflection from a surface characterized? 4. What are the conditions for equilibrium flow of light in an environment? CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

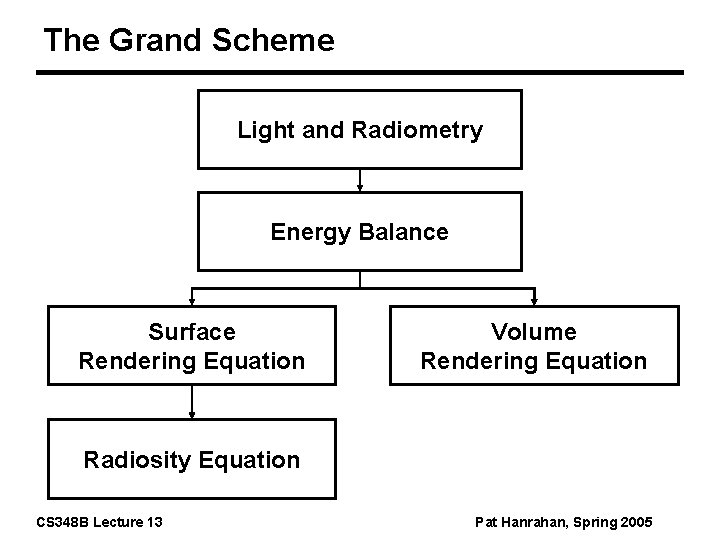
The Grand Scheme Light and Radiometry Energy Balance Surface Rendering Equation Volume Rendering Equation Radiosity Equation CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Balance Equation Accountability [outgoing] - [incoming] = [emitted] - [absorbed] n Macro level The total light energy put into the system must equal the energy leaving the system (usually, via heat). n Micro level The energy flowing into a small region of phase space must equal the energy flowing out. CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Surface Balance Equation [outgoing] = [emitted] + [reflected] CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

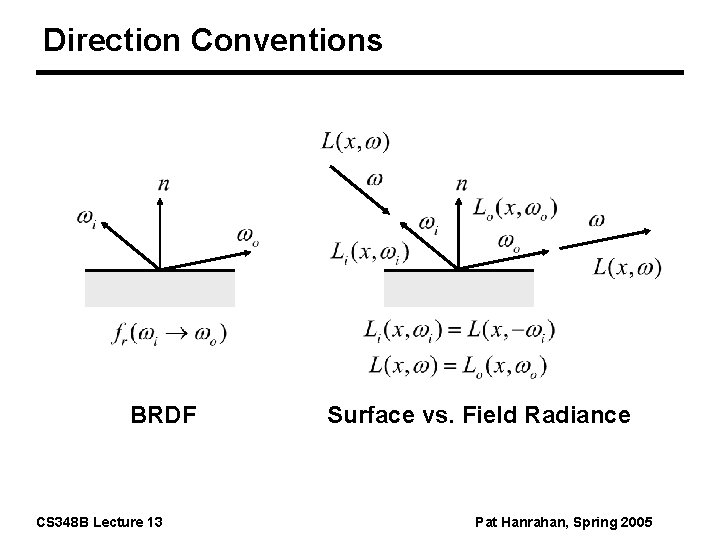
Direction Conventions BRDF CS 348 B Lecture 13 Surface vs. Field Radiance Pat Hanrahan, Spring 2005

Surface Balance Equation [outgoing] = [emitted] + [reflected] + [transmitted] BTDF CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Two-Point Geometry Ray Tracing CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Coupling Equations Invariance of radiance CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

The Rendering Equation Directional form Integrate over hemisphere of directions CS 348 B Lecture 13 Transport operator i. e. ray tracing Pat Hanrahan, Spring 2005

The Rendering Equation Surface form Geometry term Integrate over all surfaces Visibility term CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

The Radiosity Equation Assume diffuse reflection 1. 2. CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Integral Equations Integral equations of the 1 st kind Integral equations of the 2 nd kind CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Linear Operators Linear operators act on functions like matrices act on vectors They are linear in that Types of linear operators CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Rendering Operators Scattering operator Transport operator CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Solving the Rendering Equation Solution CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Formal Solution Neumann series Verify CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

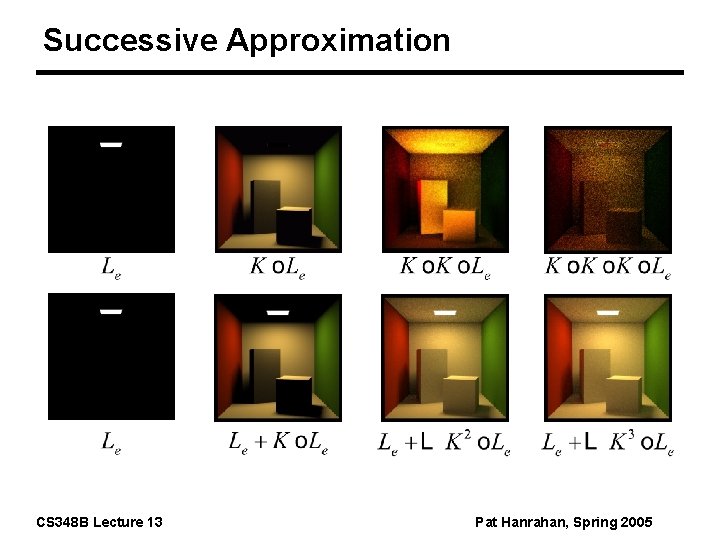
Successive Approximations Successive approximations Converged CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Successive Approximation CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

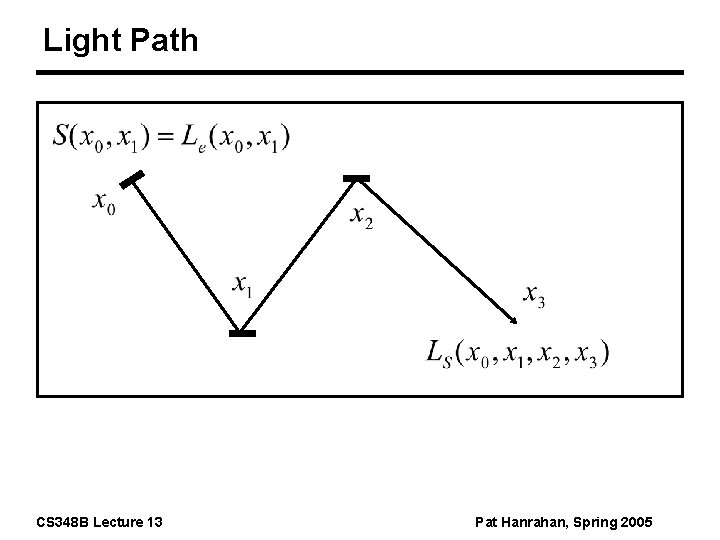
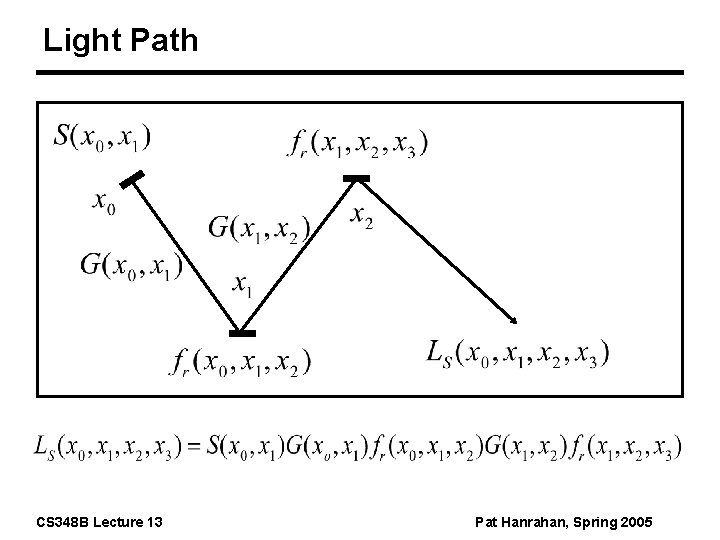
Light Path CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Light Path CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

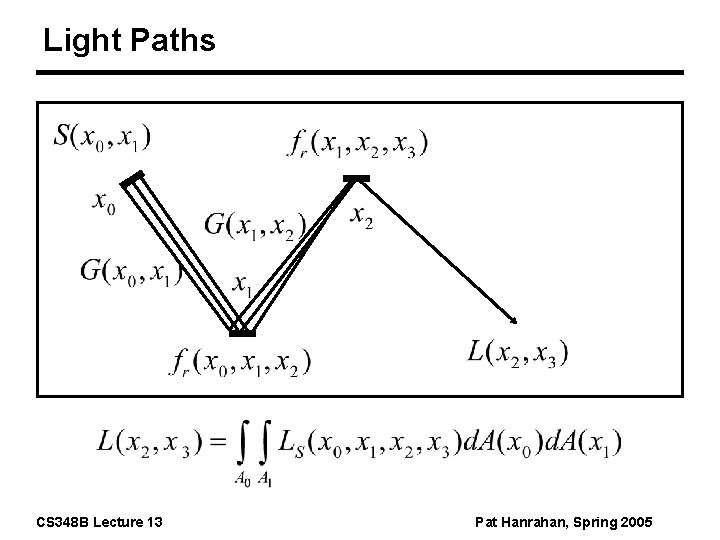
Light Paths CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

Light Transport Integrate over all paths of all lengths Question: n How to sample space of paths? CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

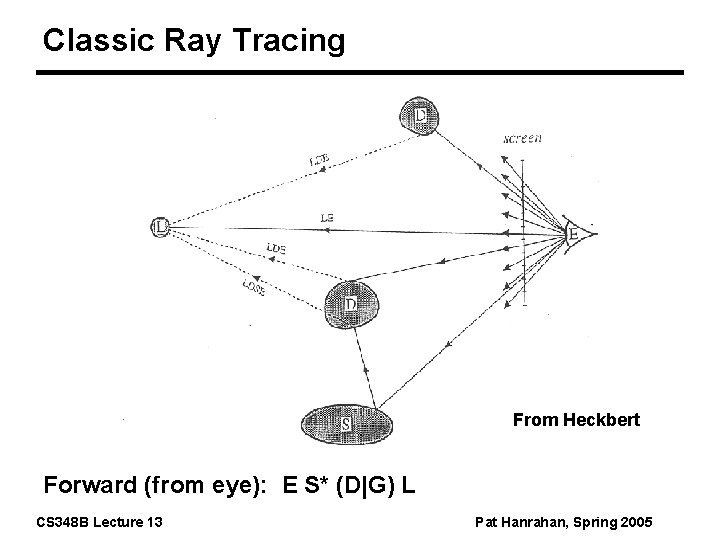
Classic Ray Tracing From Heckbert Forward (from eye): E S* (D|G) L CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

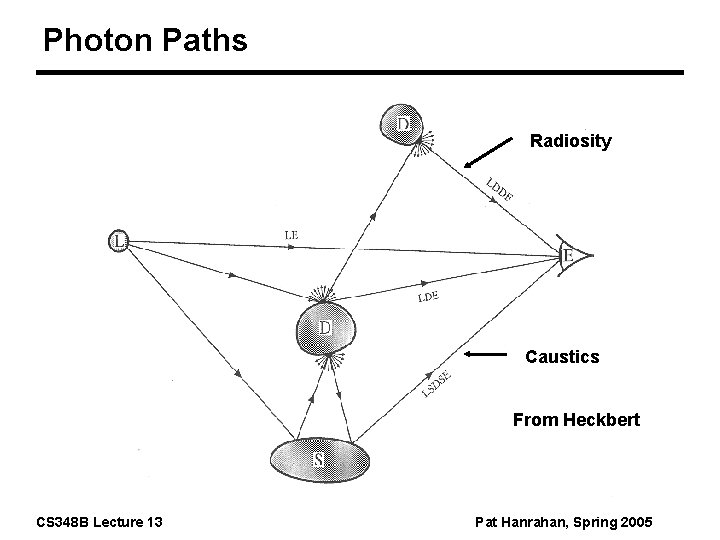
Photon Paths Radiosity Caustics From Heckbert CS 348 B Lecture 13 Pat Hanrahan, Spring 2005

How to Solve It? Finite element methods n n Classic radiosity n Mesh surfaces n Piecewise constant basis functions n Solve matrix equation Not practical for rendering equation Monte Carlo methods n Path tracing (distributed ray tracing) n Randomly trace ray from the eye n Bidirectional ray tracing n Photon mapping CS 348 B Lecture 13 Pat Hanrahan, Spring 2005