The Relational Model L 2 DB 1 Agenda

The Relational Model L 2 DB 1

Agenda • • • The Relational Algebra Operations Expressions • • L 2 DB Tuple Relational Calculus Domain Relational Calculus Implications for Query Processing Summary 2

Relational Algebra operations • • Restrict r Project p Cartesian product ´ Natural join L 2 DB • • Union Intersection Difference others 3

An example schema Book book# title author class. Code publisher year Member member# surname forename tel# address Loan book# member# due. Date Classification class. Code class. Name L 2 DB 4

Restrict r • • • The Restrict operation selects a subset of tuples from the input relation according to some condition Specified by r<selection-condition> (R) Examples: – rauthor=‘Dickens Charles’ (Books) – rdue. Date<= date(‘today’) (R) L 2 DB 5

Restrict in action Member member# surname forename tel# address 4123 Shah Hanif 1002 30 High St. 4178 Piaf Therese 1131 11, The Crest 5016 Thom Natalie 1132 11, The Crest 4268 Johns Phil 1098 77, The Lane 5286 O’Reilly Sean 1131 11, The Crest rtel#=1131 anon member# surname forename L 2 DB tel# address 4178 Piaf Therese 1131 11, The Crest 5286 O’Reilly Sean 1131 11, The Crest 6

Project p • • • The Project operation returns a subset of attributes from the input relation Specified by p<attribute-list> (R) Examples: – p author, title (Books) – p book# (R) L 2 DB 7

Project in action Member member# surname forename tel# address 4123 Shah Hanif 1002 30 High St. 4178 Piaf Therese 1131 11, The Crest 5016 Thom Natalie 1132 11, The Crest 4268 Johns Phil 1098 77, The Lane 5286 O’Reilly Sean 1131 11, The Crest Ptel#, surname anon tel# surname 1002 Shah 1131 Piaf 1132 Thom 1098 Johns 1131 O’Reilly L 2 DB 8

Cartesian Product ´ • • The Product operator takes in two relations and produces an output in which every tuple in the first relation is matched with every row in the second relation Specified by – R 1 ´ R 2 • Note: The operator takes its name from Rene Descartes, the French philosopher mathematician L 2 DB 9
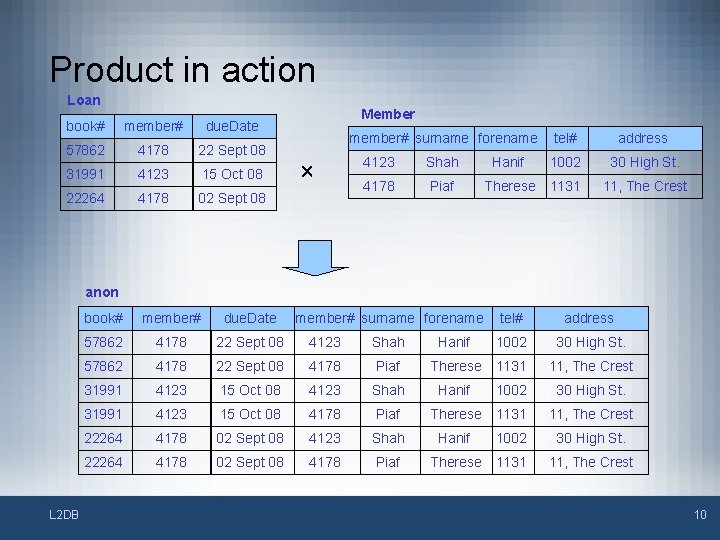
Product in action Loan book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 22264 4178 02 Sept 08 Member member# surname forename ´ tel# address 4123 Shah Hanif 1002 30 High St. 4178 Piaf Therese 1131 11, The Crest anon L 2 DB book# member# due. Date member# surname forename tel# address 57862 4178 22 Sept 08 4123 Shah Hanif 1002 30 High St. 57862 4178 22 Sept 08 4178 Piaf Therese 1131 11, The Crest 31991 4123 15 Oct 08 4123 Shah Hanif 1002 30 High St. 31991 4123 15 Oct 08 4178 Piaf Therese 1131 11, The Crest 22264 4178 02 Sept 08 4123 Shah Hanif 1002 30 High St. 22264 4178 02 Sept 08 4178 Piaf Therese 1131 11, The Crest 10

Natural join • • Natural join is the most common form of Join operation. It combines the data from two relations by matching values on attributes with the same name. Specified by – R 1 L 2 DB R 2 11

Natural join in action Loan book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 22264 4178 02 Sept 08 Member member# surname forename tel# address 4123 Shah Hanif 1002 30 High St. 4178 Piaf Therese 1131 11, The Crest anon book# member# due. Date surname forename tel# address 57862 4178 22 Sept 08 Piaf Therese 1131 11, The Crest 31991 4123 15 Oct 08 Shah Hanif 1002 30 High St. 22264 4178 02 Sept 08 Piaf Therese 1131 11, The Crest Note: the effect of a natural join can be achieved by a Cartesian Product followed by a Restrict and a Project - see if you can work out how. L 2 DB 12

Union • • Union takes in two compatible relations and returns a relation that contains the tuples that appear in either or both. The relational algebra demands that the input relations are compatible, i. e. they are of the same type L 2 DB 13
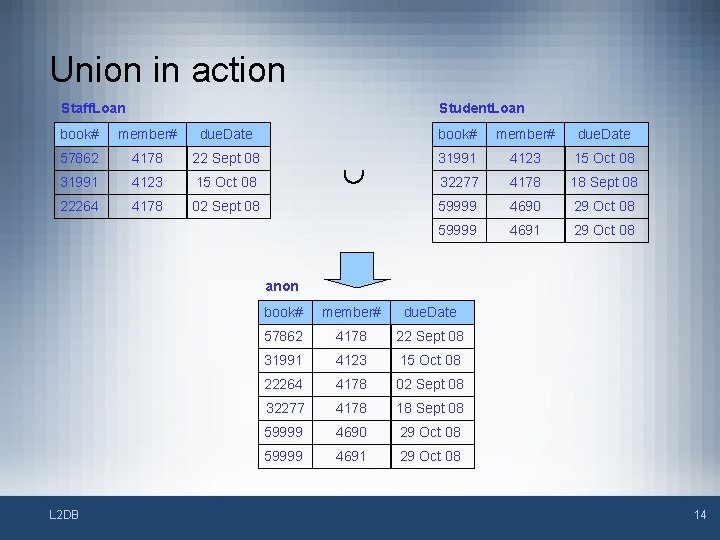
Union in action Staff. Loan Student. Loan book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 32277 4178 18 Sept 08 22264 4178 02 Sept 08 59999 4690 29 Oct 08 59999 4691 29 Oct 08 anon L 2 DB book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 22264 4178 02 Sept 08 32277 4178 18 Sept 08 59999 4690 29 Oct 08 59999 4691 29 Oct 08 14

Intersection • • Intersection takes in two compatible relations and returns a relation that contains the tuples that appear in both. Again the relational algebra demands that the input relations are compatible, i. e. they are of the same type L 2 DB 15
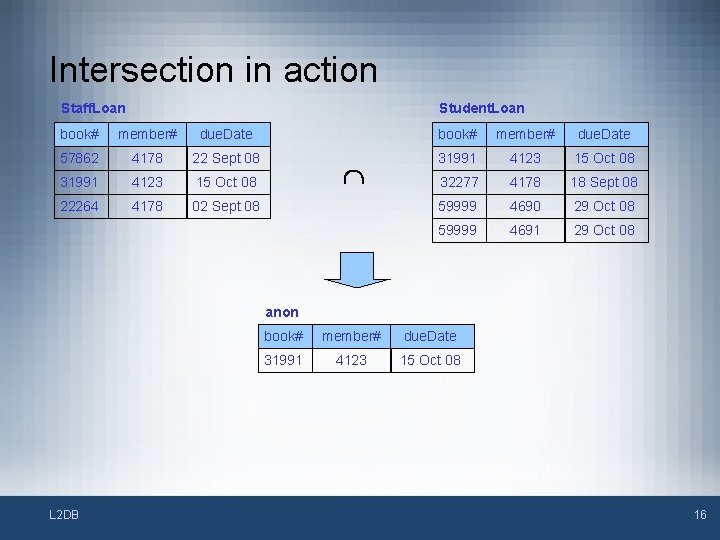
Intersection in action Staff. Loan Student. Loan book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 32277 4178 18 Sept 08 22264 4178 02 Sept 08 59999 4690 29 Oct 08 59999 4691 29 Oct 08 anon L 2 DB book# member# due. Date 31991 4123 15 Oct 08 16

Difference • The difference operator takes in two compatible relations X and Y and returns a relation that contains the tuples that appear in X but NOT in Y L 2 DB 17

Difference in action Staff. Loan Student. Loan book# member# due. Date 57862 4178 22 Sept 08 31991 4123 15 Oct 08 22264 4178 02 Sept 08 - book# member# due. Date 31991 4123 15 Oct 08 32277 4178 18 Sept 08 59999 4690 29 Oct 08 59999 4691 29 Oct 08 anon L 2 DB book# member# due. Date 57862 4178 22 Sept 08 22264 4178 02 Sept 08 18

Other operators • Codd originally described a set of eight operators – Some of these operators are not essential because they can be derived from others • Many authors have contributed further operators to the algebra – divide, semijoin, outer join, … • The set of operators provided in any relational implementation is relationally complete if it is at least as powerful as Codd’s original set. L 2 DB 19

Relational Algebra expressions • • The power of relational algebra arises from its ability to compose expressions Examples – p title (rauthor=‘Greene Graham’ (Book)) • will return the titles of books written by Graham Greene – p title, author(rmember#=4128 (Loan Book)) • will return the titles and authors of books on loan to library member 4128 L 2 DB 20
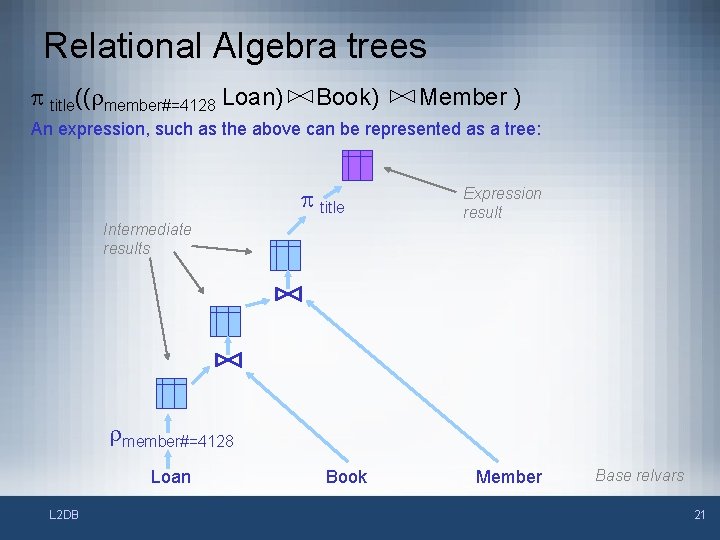
Relational Algebra trees p title((rmember#=4128 Loan) Book) Member ) An expression, such as the above can be represented as a tree: p title Intermediate results Expression result rmember#=4128 Loan L 2 DB Book Member Base relvars 21

Equivalence of algebra expressions Consider the following two expressions p title, surname((rmember#=4128 Loan) ptitle, surname(rmember#=4128 ((Loan Book)) Book) Member ) (psurname, member#Member ))) The expressions are quite different in the operations, particularly in the order in which the operations are applied. However, the two expressions will always yield the same result i. e. the expressions are equivalent. If we consider, the size of the intermediate results and the number of tuples processed by each operator, we can assess that the first expression is likely to be more efficient than the second. L 2 DB 22

Implications for Query Processing – The database query language SQL is (loosely) based on the tuple relational calculus – The database query language QBE is based on the domain relational calculus – Either of these can be converted into relational algebra, which provides a processing model to execute the query – In a relational DBMS a software component known as a Query Optimizer converts a query into an efficient operation tree that is similar to the relational algebra L 2 DB 23

Summary • The relational model comprises: – a structural specification – a means of enforcing integrity – a means of manipulating data • The model – provides a solid theoretical basis for database processing, based on set theory and first-order predicate logic – supplies the foundation for relational DBMS implementation L 2 DB 24

Caveat • • Commercial RDBMS products and the SQL standard language are based on the relational model However, none of them conform to the relational model – the extent to which existing systems deviate from the model and the implications of this is a matter of great controversy – see the reading list for further study of this area L 2 DB 25
- Slides: 25