The Relational Algebra What operations can be done

The Relational Algebra What operations can be done? Creative Commons License – Curt Hill

Algebra • There exists a relational algebra • What is an algebra? • What most of us know as Algebra is actually the Algebra of Real Numbers • There is also Boolean Algebra among others Creative Commons License – Curt Hill

Algebra of Real Numbers • What does this Algebra consist of? • A set of objects to work on – This is the infinite set of real numbers • A set of operators – These include , , , – The may be subtraction or negation – Each operator takes one or two real numbers and computes another real – There are rules on how they must be applied Creative Commons License – Curt Hill

Relational Algebra • Similar in concept, different in objects and operators • The object that it operates on are not real numbers but tables – Sets of relations • It also possesses operators – Each takes one or two tables and produces another table • These are considered shortly Creative Commons License – Curt Hill

Relations • Ordered pairs express relationships – As do any tuples • A set of tuples define a relation • Recall that a set is composed of unique items and is not ordered • In databases the primary key must be unique – Not every field needs to be unique Creative Commons License – Curt Hill

Example • An example relation is the origin, destination and departure of airline flights, key is entire tuple – (Fargo, Bismarck, 14: 20) – (Fargo, Minneapolis, 8: 40) – (Fargo, Winnipeg, 12: 00) – (Fargo, Minneapolis, 16: 10) – (Minneapolis, Fargo, 10: 40) – (Minneapolis, St. Louis, 7: 55) • When we see a set of tuples, they are always a relation Creative Commons License – Curt Hill

• • Operations Selection Projection Cartesian product Set union Set intersection Set difference First two take one table, the rest two The above are primitive operations – There also composite operations made of several primitives Creative Commons License – Curt Hill

Operations • Relational operations are like arithmetic operations • They are unary or binary – One operand or two • They take operands and produce a result • The operands and results are always tables – Perhaps an empty table Creative Commons License – Curt Hill

Selection • Choose or eliminate tuples based on a comparison • Unary operation • There is a boolean test which determines if a row is eliminated or not • The symbol is the sigma (s) • The resulting table always has same degree, but usually smaller cardinality Creative Commons License – Curt Hill

Boolean test of selection • The test may include – Fields compared with constants – Fields compared with other fields in same record • The test may be ANDed, ORed or NOTted together to make it more powerful Creative Commons License – Curt Hill

Selection Example T 1 ID A B C E Cnt 1 5 2 3 s cnt > 2(T 1) Src X X W Z Use 18 4 16 12 ID B E Frq 5 5 4 9 Cnt 5 3 Creative Commons License – Curt Hill Result Src X Z Use Frq 4 5 12 9

Projection • • Choose or eliminate columns Unary operation We may also rearrange the columns Since the relation is a set the rows do not need to be in the same order • The symbol is pi (p) • The result has same cardinality but is less than or equal to the original degree Creative Commons License – Curt Hill
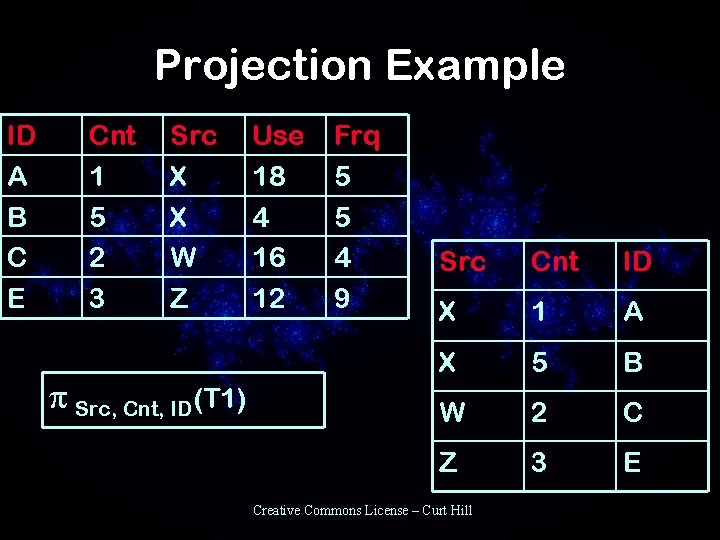
Projection Example ID A B C E Cnt 1 5 2 3 Src X X W Z p Src, Cnt, ID(T 1) Use 18 4 16 12 Frq 5 5 4 9 Src Cnt ID X 1 A X 5 B W 2 C Z 3 E Creative Commons License – Curt Hill

More Projection Notes • Usually projection is used to change degree of relation • A relation is a set – It must have unique entries before a projection – This may not be so when an attribute is removed • Projection may produce duplicates than need to be eliminated – Not all systems actually do this – Why not? Creative Commons License – Curt Hill
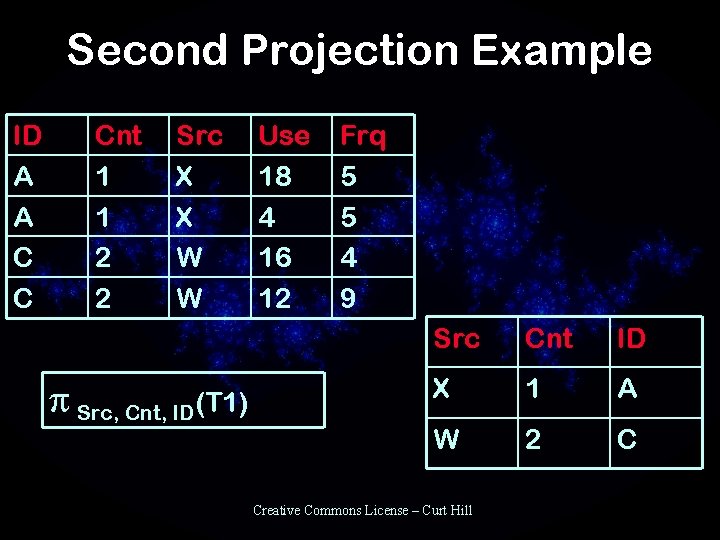
Second Projection Example ID A A C C Cnt 1 1 2 2 Src X X W W p Src, Cnt, ID(T 1) Use 18 4 16 12 Frq 5 5 4 9 Src Cnt ID X 1 A W 2 C Creative Commons License – Curt Hill

Cartesian Product • AKA Cross product or cross join • Binary operation • Append to each row in first each row in the second • The cardinality in the result is the product of the two cardinalities • The degree is the sum of degrees • The two relations can be of different types Creative Commons License – Curt Hill

Cartesian Product Example ID A B A B Cnt 1 5 1 5 T 1 T 2 F 1 A A X X B B F 2 6 6 4 4 3 3 F 3 1 1 2 2 9 9 F 1 F 2 F 3 A X 6 4 1 2 B 3 9 Creative Commons License – Curt Hill

Cartesian Addendum • Only primitive operator that deals with two different schemas • If the two tables have a common field, one of the fields must be renamed – A tuple must be a set with unique field names • Very expensive operation – In a normal database only done with optimization Creative Commons License – Curt Hill

Cartesian Product Example ID A B A B Cnt 1 5 1 5 T 1 T 2 ID 2 A A X X B B Cnt 2 6 6 4 4 3 3 Src 1 1 2 2 9 9 ID Cnt Src A X 6 4 1 2 B 3 9 Creative Commons License – Curt Hill

Set Union • • Binary operation Two relations must be union compatible – They must have same schema, that is the same attributes • New relation has all the tuples of both tables with duplicates removed Creative Commons License – Curt Hill
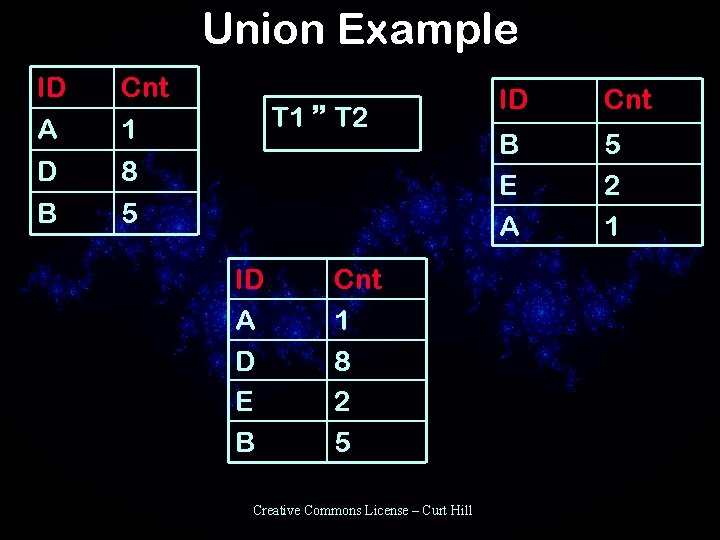
Union Example ID A D Cnt 1 8 B 5 T 1 T 2 ID A D E B Cnt 1 8 2 5 Creative Commons License – Curt Hill ID Cnt B E A 5 2 1

Set Intersection • • Binary operation Two relations must be union compatible – They must have same schema, that is the same attributes • New relation has only the tuples in both tables Creative Commons License – Curt Hill
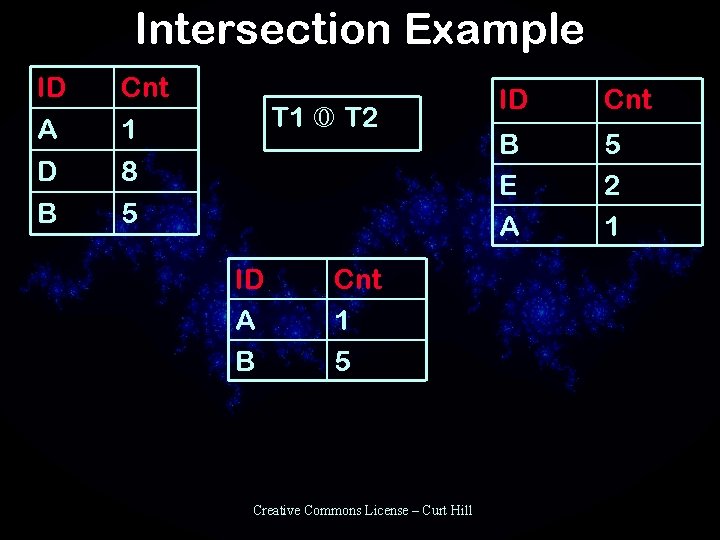
Intersection Example ID A D Cnt 1 8 B 5 T 1 T 2 ID A B Cnt 1 5 Creative Commons License – Curt Hill ID Cnt B E A 5 2 1

Set Difference • • Binary operation Two relations must be union compatible – They must have same schema, that is the same attributes • • New relation has only the tuples in both tables removed from first table Not symmetrical or commutative Creative Commons License – Curt Hill

Set Difference Example ID A D Cnt 1 8 B 5 Cnt 8 Cnt B E A 5 2 1 T 2 – T 1 - T 2 ID D ID ID E Creative Commons License – Curt Hill Cnt 2

Relational Algebra • The algebra only uses these operations – All of our queries translate into these • Each operation produces a relation – Starts with one or two relations • The algebra is closed – Maps from the set of relations back to the set of relations • There also composite operations Creative Commons License – Curt Hill

Join • Binary composite operation • It is the composite of three operations – Cartesian product – Selection – Projection (optional) • Often the only way cartesian products are done – Thus the DBMS may optimize it Creative Commons License – Curt Hill

Join • A join always operates on joining the two tables through a common field (or fields) in each • Thus we join on one or more fields that are in common between the two tables – The fields must have the same format, often have same name Creative Commons License – Curt Hill

Join Process • Take the product of the two tables • Use select to eliminate all records where the two fields are not equal • Eliminate one of the redundant fields • Resulting table as the sum of the two tables field minus one • The number of rows is dependent on data Creative Commons License – Curt Hill
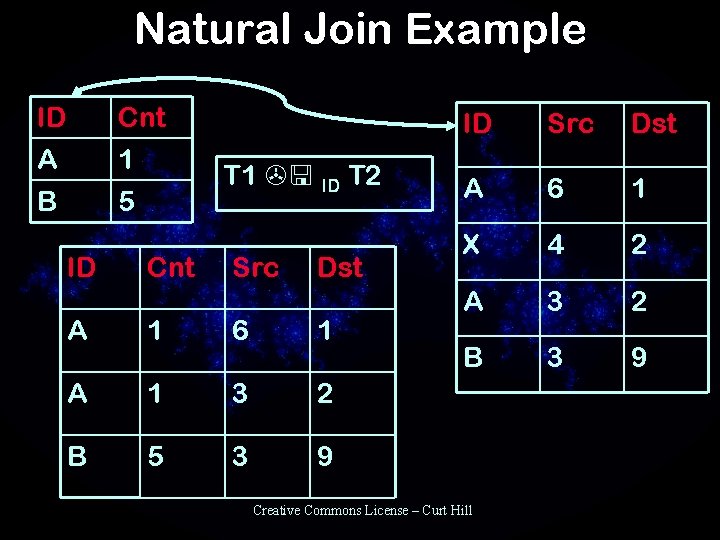
Natural Join Example ID A B Cnt 1 5 ID Cnt T 1 ID T 2 Src Dst A 1 6 1 A 1 3 2 B 5 3 9 ID Src Dst A 6 1 X 4 2 A 3 2 B 3 9 Creative Commons License – Curt Hill

Types of Joins • The relationship between the two joined fields may be anything – We specify the fields and comparison – Called a Condition Join – Same schema as product • When comparison is equality the join is called an Equijoin – Project on equijoin to eliminate redundant column • If the join is equijoin on all common fields then it is called a Natural Join Creative Commons License – Curt Hill

Condition Join Example ID A B Cnt 5 3 ID Cnt Dst A X 6 4 1 2 T 1. Cnt<T 2. Cnt T 2 B 3 9 ID A B B Cnt 5 3 3 ID 2 A A X Cnt 2 6 6 4 Creative Commons License – Curt Hill Dst 1 1 2

Join Importance • The cartesian product is only primitive that may take two different relation types • Cartesian products are usually inside a join • Usually one table in a database has a particular schema • Almost every multiple table queries will use a join Creative Commons License – Curt Hill

Division • Division a composite not primitive operation • Deals with three relations of different degree – First table degree m+n – Second of degree n – Result of degree m • Columns in the second table are eliminated from the first Creative Commons License – Curt Hill

Division Process • The columns in the second table correspond to those in the first • If the values in the first table match any corresponding values in the second the row is copied to result • The common columns are eliminated in the result • Duplicates are then eliminated Creative Commons License – Curt Hill
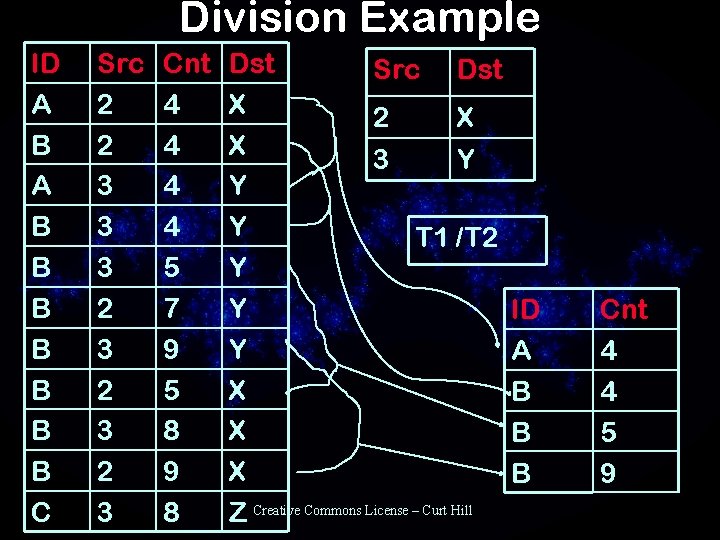
Division Example ID A B B B B C Src 2 2 3 3 3 2 3 2 3 Cnt 4 4 5 7 9 5 8 9 8 Dst Src Dst X 2 X X 3 Y Y Y T 1 /T 2 Y Y ID Y A X B X B Z Creative Commons License – Curt Hill Cnt 4 4 5 9

Division Implementation • Do an equijoin on the two tables common columns • Project away the remaining common columns Creative Commons License – Curt Hill

Algebra and Calculus • The algebra is procedural – You specify how to do what needs to be done – Must use the operations • The calculus is declarative – You say what you want without saying how to obtain this • SQL has elements of both • Calculus must be translated into the algebra before execution Creative Commons License – Curt Hill

Algebra Shortcomings • Algebra is a theoretical support for database implementation • It lacks most of the niceties needed for an actual implementation – Reports – Formatting – Counts – Averages • All it does is deliver the data as a table Creative Commons License – Curt Hill

Queries using relational algebra • Consider the college schema tables: – Course – Students – Grade – Faculty_teach – Department – Division Creative Commons License – Curt Hill

Example • Suppose we want to produce a grade report for students • This should include information from two or three relations: – Students – Grade – Courses (depending how much information is needed) Creative Commons License – Curt Hill
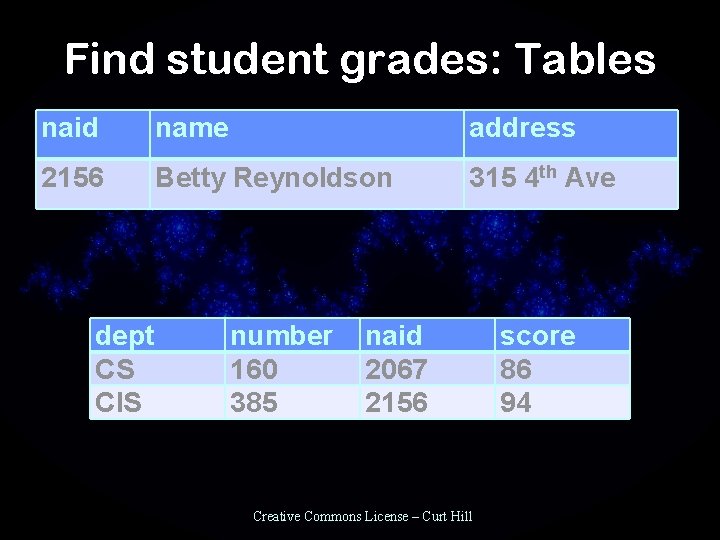
Find student grades: Tables naid name address 2156 Betty Reynoldson 315 4 th Ave number 160 385 score 86 94 dept CS CIS naid 2067 2156 Creative Commons License – Curt Hill

Find student grades: Operations • Equi join on ID – Students NAID Grades • Project away unwanted fields –p name, dept, course, score – Include address if it is to be mailed • Outside of the algebra – Format score as grade – Sort by zip code – Format into pages Creative Commons License – Curt Hill

Find all the courses taught by faculty members • Equi join on ID – Faculty NAID Faculty_teach • Project away unwanted fields –p name, dept, course Creative Commons License – Curt Hill

Find the departmental chairs for each faculty member • Equi-join on ID – Faculty NAID Departments • This connects departments and chairs – p name, dept • Equi join on ID – Faculty Dept Temp • Project out what is not needed • Two more joins needed to include divisional chairs Creative Commons License – Curt Hill

Find all the students who got a B or better in any CS class • • • Use selection to trim the grades relation to just CS acronym, ID and score greater than or equal to 80 Join this with students based on student ID equality Eliminate those columns that you do not want Creative Commons License – Curt Hill

Find all the students that each faculty member has • • • Join faculty with faculty_teach on NAID Join this with grades file based on equality with both dept acronym and course number Project out what you don’t want Creative Commons License – Curt Hill

Find all the students who got an A in Calculus and an A in CIS 385 • Select out all the grades table leaving only Calc As • Join this with students on NAID Call this T 1 • Select out all the grades table leaving only CIS 385 As • Join this with students on NAID and call it T 2 • Intersect T 2 Creative Commons License – Curt Hill

Find this semesters GPA of all Math students • What is a Math student? – – • A Math major or Any student taking any math course Is this the average score of math courses? – • If so, do a selection on grades table Is this the average score of all students taking any math course? – – Select grades to just find Math Join this with student on NAID Join this with original grade file Use report program to sort by NAID and then compute and summarize the GPA Creative Commons License – Curt Hill
- Slides: 49