The Recursive Descent Algorithm A useful predictive parser

The Recursive Descent Algorithm A useful predictive parser for many applications. Under Construction (Nov 16) 1

The Recursive Descent Algorithm q q q The recursive descent algorithm directly implements a grammar written as EBNF rules. The rules should not contain left recursion There is one function (method) for each EBNF rule. Each method parses the input corresponding to its EBNF rule, and returns a value. The value may be: n a node on the abstract syntax tree of the input n value computed by evaluating the input (e. g. a calculator) Recursive descent is a predictive parser. Limited look-ahead ("peek" at the next token) can be incorporated. 2

Recursive-descent intro (0) Grammar: expr => expr + term | expr - term | term => term factor | factor => '(' expr ')' | number 3

Recursive-descent intro (0. 5) Grammar in EBNF (no "self-recursion"): expr => term { ( + | -) term } term => factor { factor } factor => '(' expr ')' | number 4

Recursive-descent intro (1) q q Grammar: expr => term { + term } term => factor { factor } factor => '(' expr ')' | number Generic C code for concept only (don't use this): expr() { term(); while(token=='+') { match('+'); term(); } } term() { factor(); while(token=='*') { match('*'); factor(); } } 5

Recursive-descent intro (2) q q Grammar: expr => term { + term } term => factor { factor } factor => '(' expr ')' | number Factor and number: factor() { if (token == ‘(‘) { match('('); expr( ); match(‘)’); } else number( ); } number() { if ( is. Number(token) ) { add_to_parse_tree(); next. Token( ); } else error("invalid number"); } 6

Recursive-descent intro (3) match(value) is a utility that requires a match: if current token matches the argument, consume the token and get next token. q Otherwise print an error. . and then what? q void match(char what) { if ( *token == what ) { next. Token( ); } else { /* 'printf' style error function */ error("expected %c got %s", what, token); } } 7

Where's the token? q q In this algorithm, token is a global variable that always contains the next unread token. next. Token() returns true if there are more tokens, and also sets the token variable. boolean next. Token( ) { token = scanner( ); return ( token != EOF ); } q Another utility function is match(value): 1) if value matches token, get a new token 2) if value doesn't match, raise an error condition. 8

Where's the output? In the generic algorithm, the result is a global variable. q The methods must either return a value or accumulate value as a side effect. q Rules which have terminal values should return the terminal value. q factor => ( expr ) | number q number() { if ( is. Number(token) ) { // add token to the parse tree // or return a value } else error("invalid number"); } 9

Recursive Descent Example (1) Let's look at a recursive descent code for a calculator. We will modify the generic algorithm so that each function returns a double value. input: expr 'n' expr: term { (+|-) term } term: factor { (*|/) factor} factor: '(' expr ')' | number 10

Recursive Descent Example (1) Let's look at a recursive descent code for a calculator. We will modify the generic algorithm so that each function returns a double value. Example: here is a modified expr( ) function double expr() { double expr = term(); while( token =='+' || token =='-' ) ) { if (token == '+') { match('+'); Grammar Rule: expr = expr + term(); expr: term { (+|-) term } } else { match('-'); expr = expr - term(); } } return expr ; } 11

Recursive Descent Example (2) The rule for factor is more interesting: we must check the first token to decide which alternative to use, then double factor() { double fact; if ( token == '(' ) { next. Token( ); fact = expr( ); match( ')' ); return fact; } else { fact = number( ); return fact; } } Grammar Rule: factor: '(' expr ')' | number 12

Recursive Descent Example (3) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "2" input line token = next. Token(); ans = expr( ); 13

Recursive Descent Example (4) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "2" input line expr ans = expr( ); expr = term( ); expr( ) { expr = term( ); while ( token=='+'|| token='-') { if ( token=='+' ) { match('+'); expr = expr + term( ); } else { match('-'); expr = expr - term( ); } return expr; 14

Recursive Descent Example (5) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "2" input line ans = expr( ); expr = term( ); term = factor( ); term( ) { term = factor( ); while ( token=='*' || token=='/' ) { if ( token=='*' ) { match('*'); term = term * factor( ); } else { match('/'); term = term / factor( ); } 15

Recursive Descent Example (6) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "*" input line ans = expr( ); expr = term( ); term = factor( ); factor fact = number( ); /* token = '*' */ return factor( ) { if ( token=='(' ) { match('('); fact = expr( ); match(')'); } else { fact = number( ); } 16

Recursive Descent Example (7) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "3" input line ans = expr( ); expr = term( ); term = 2; term( ) { term = factor( ); term = term while ( token=='*' * factor( ); || token='/' ) { if ( token=='*' ) { match('*'); term = term * factor( ); } else { match('/'); term = term / factor( ); } 17

Recursive Descent Example (8) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "+" input line ans = expr( ); expr = term( ); term = term * factor( ); factor fact = number( ); /* token = '*' */ return factor( ) { if ( token=='(' ) { match('('); fact = expr( ); match(')'); } else { fact = number( ); } 18

Recursive Descent Example (9) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "+" input line ans = expr( ); expr = term( ); term = term * 3; return term( ) { term = factor( ); while ( token=='*' || token=='/' ) { if ( token=='*' ) { match('*'); term = term * factor( ); } else { match('/'); term = term / factor( ); } 19

Recursive Descent Example (10) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "(" input line expr ans = expr( ); expr = 6; token = '+' match('+') expr = expr + term( ) expr( ) { expr = term( ); while( token=='+'|| token=='-') { if ( token=='+' ) { match('+'); expr = expr + term( ); } else { match('-'); expr = expr - term( ); } return expr; 20

Recursive Descent Example (11) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "(" input line ans = expr( ); expr = term( ); term = factor( ); term( ) { term = factor( ); while ( token=='*' || token=='/' ) { if ( token=='*' ) { match('*'); term = term * factor( ); } else { match('/'); term = term / factor( ); } 21

Recursive Descent Example (12) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "4" input line ans = expr( ); expr = term( ); term = term * factor( ); factor match('(') fact = expr( ); factor( ) { if ( token=='(' ) { match('('); fact = expr( ); match(')'); } else { fact = number( ); } return fact; 22

Recursive Descent Example (13) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "4" input line ans = expr( ); expr = term( ); term factor expr( ) { expr term = term * factor( ); = term( ); while (token=='+'|| token=='-') fact = expr( ); { if ( token=='+' ) { match('+'); expr = term( ); expr = expr + term( ); } else { match('-'); expr = expr - term( ); } return expr; 23

Recursive Descent Example (14) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "-" input line ans = expr( ); expr = term( ); term = term * factor( ); factor fact = expr( ); expr = term( ); term = factor( ); factor fact = number( ); /* = 4, token = "-" */ 24

Recursive Descent Example (15) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "-", then token = "5" input line ans = expr( ); expr = term( ); term factor expr( ) { expr term = term * factor( ); = term( ); while (token=='+'|| token=='-') fact = expr( ); { if ( token=='+' ) { match('+'); match('-') expr = expr + term( ); expr = expr } else { - term( ); match('-'); expr = expr - term( ); } return expr; 25

Recursive Descent Example (16) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "5" input line ans = expr( ); expr = term( ); term = term * factor( ); factor fact = expr( ); expr = expr - term( ); term = factor( ); factor fact = number( ); /* = 5. token = ")" */ 26

Recursive Descent Example (16) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "/" input line ans = expr( ); expr = term( ); term = factor( ); term( ) { term = factor( ); while ( token=='*' fact = expr( ); || token=='/' ) { match(')'); return fact; if ( token = '*' ) { expr = 4 - 5; return expr. . . } term = 5; return term; factor return 5 factor expr 27

Recursive Descent Example (17) Input: 2 * 3 + ( 4 - 5 ) / 6 Progress: token = "6" input line ans = expr( ); expr = term( ); term = -1; match('/') term = term / factor( ); term( ) { term = factor( ); while ( token=='*' || token=='/' ) { if ( token=='*' ) { match('*'); term = term * factor( ); } else { match('/'); term = term / factor( ); } 28

Imperative Approach to Parsing In the generic algorithm, the token is a global variable, and the results of the parse are a side effect (a change to global variables or structures) q bison and flex operate this way, too. q Programs difficult to understand maintain. q No error recovery in generic algorithm. q /* yylex uses global variables / constants. */ int yylex( ) {. . . if ( isdigit(c) ) { ungetc(c, stdin); scanf("%lf", &yylval); return INT; } } 29

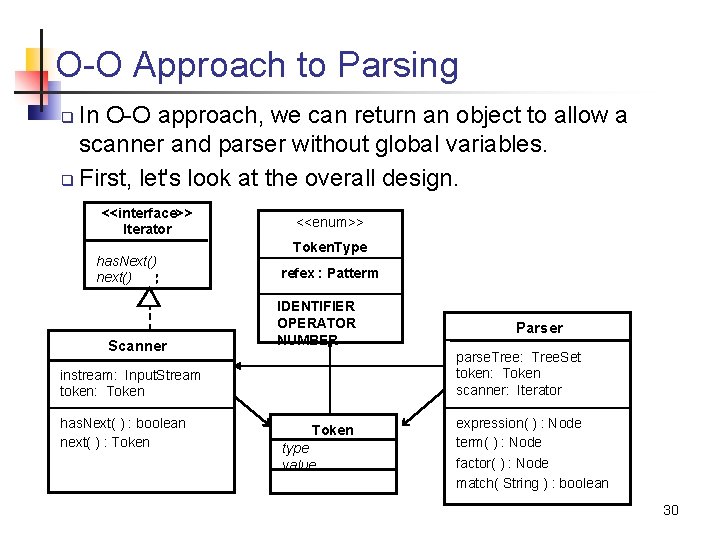
O-O Approach to Parsing In O-O approach, we can return an object to allow a scanner and parser without global variables. q First, let's look at the overall design. q <<interface>> Iterator has. Next() next() Scanner <<enum>> Token. Type refex : Patterm IDENTIFIER OPERATOR NUMBER parse. Tree: Tree. Set token: Token scanner: Iterator instream: Input. Stream token: Token has. Next( ) : boolean next( ) : Token Parser Token type value expression( ) : Node term( ) : Node factor( ) : Node match( String ) : boolean 30

O-O Scanner The Scanner should provide two services: test for more tokens and return the next token. q In this view, a Scanner looks like an Iterator<Token>. q A "token" has both a type and a value. q /** Token class */ public class Token { Type type; /* consider an enumeration */ public Object value; /* can be anything */ public Token(Type type, Object value) {. . . } public Object get. Value( ) {. . . } } 31

O-O Parser The Parser implements the parsing algorithm. q Result is either a parse tree or a value (calculator application). q Use an attribute to represent next token. q /** Parser class */ public class Parser { Iterator<Token> scanner; private Token token; private Tree. Node result; /* parse tree */ Tree. Node expression( ) {. . . }; Tree. Node term( ) {. . . }; Tree. Node factor( ) {. . . }; boolean match( String what ) {. . . }; boolean match( Type what ) {. . . }; } 32

O-O Parser for Calculator For a calculator, the parser can compute result. q Can use a primitive data type for expression, etc. q /** Parser class */ public class Parser { Iterator<Token> scanner; private Token token; private double result; double expression( ) {. . . }; double term( ) {. . . }; double factor( ) {. . . }; boolean match( String what ) {. . . }; } 33

Observation: match If the generic algorithm, the token is almost always tested before calling match. q Eliminate redundancy by redefining match(value) to return a boolean value if token matches. q if match, then consume the token. q private boolean match( String what ) { if ( ! (token. value instanceof String) ) return false; if ( what. equals( (String)(token. value) ) ) { token = scanner. next( ); return true; } return false; } 34

O-O Parser for Calculator (2) Example method: expression q EBNF: expr : : = term { (+ | -) term } q private double expression( ) { double result = term( ); while( true ) { if ( match("+") ) result += term( ); else if ( match("-") ) result -= term( ); else break; /* why not error( )? */ } return result; } 35

O-O Parser : Top-Level What is the top-level routine of the parser? q Look at standard bison code for inspiration: q %% input line /* Bison grammar rules */ : /* empty input */ | input line ; : expr 'n' { output( $1 ); } ; 36

Parsing Errors How are you going to handle parsing errors? q You might have many levels of function calls. . . q input line result = expr( ); expr = term( ) term = factor( ) factor = '(' expr() ')' | number(). . . ; expr term factor { +|- term( ) }; { *|/ factor( ) }; Using recursive-decent, parse errors are usually detected at the bottom of the tree: in factor, number, etc. Parse error found here 37

Parsing Errors q If you set an error flag or return an error result, then all the methods must check for this condition. . . input line if ( error ) print "parse error"; expr if ( error ) return /* what value? */; term if ( error ) return /* what value? */; factor if ( error ) return /* what value? */; expr if ( error ) return /* what value? */; term if ( error ) return /* what value? */; factor This error checking will make your methods longer and harder to understand. Parse error found here 38

Throwing an Exception q Your code will be simpler if the methods simply throw an exception, and let the top-most method catch it. input line try { result = expr( ); } catch (Parse. Exception e) {/*error*/} expr( ) throws Parse. Exception {. . . } term( ) throws Parse. Exception {. . . } Let factor( ) throws Parse. Exception {. . . } someone expr( ) throws Parse. Exception {. . . } term( ) throws Parse. Exception {. . . } factor else handle it! throw new Parse. Exception( ) 39

Using Java's Parse. Exception q Java has a Parse. Exception class you can use: java. text. Parse. Exception q the constructor requires two parameters: new Parse. Exception("error message", offset); q Example: number( ) { /* parse a number */ whitespace(); token = tokenizer. next(); if ( token. type != Token. Type. NUMBER ) throw new Parse. Exception( "invalid number", cptr); 40

Defining your own Parse. Exception q You can define a new Exception type for your own use import java. io. IOException; class Parse. Exception extends IOException { /* constructors */ Parse. Exception() { super("Parse Error"); } Parse. Exception(String msg) { super(msg); } Parse. Exception(String msg, int column) { super(msg + " in column " + column); } } 41

Using Parse. Exception q q q You should try to return useful error messages, such as. . . factor( ) { if ( match('(') ) { result = expr( ); if ( ! match(')') ) throw new Parse. Exception("missing right parenthesis"); } The get. Message( ) method returns the error message. . . try { result = expr( ); } catch(Parse. Exception e) { println( e. get. Message() ); } Including the column number in error messages can be helpful. 42

Parsing Unary Minus Sign q q q Parsing negative numbers and unary minus can also be tricky. The following are valid expressions in most languages: sum = sum + -1; sum = sum - -2; sum = sum * -x; The GNU C compiler (gcc) allows a space after the unary "-" : sum = sum - - 2; Exponentiation has higher precedence than unary minus, so it should be incorporated in a rule at the bottom of your grammar rules: -2 ^ 3 means - (2^3) 43

What's Next? Later we will add to the implementation. . . q symbol table and assignments x a b y q q = = 3. 5 E 7 5 0. 1 ( a*x + b ) / ( a*x - b ) built-in functions y = sqrt( x ) user defined functions function f(x) = a*x + b f(0. 5) 44