The question Can we generate provable random numbers

The question Can we generate provable random numbers? ? 101101101000010010001111101001001111010100 ….

Why it matters Security of protocols like RSA breaks down if randomness is bad. [Lenstra+ 12, Heninger+ 12] P, Q (primes)

Existing solutions “[We assume] that the developer understands the behavior of the entropy source and has made a good-faith effort to produce a consistent source of entropy. ” Can we generate randomness without assuming good faith?

Quantum random number generation • Untrusted-device randomness expansion • Untrusted-device randomness amplification • Semi-device-independent random number generation. • Contextuality-based randomness expansion. • Randomness extraction.

Quantum random number generation • Untrusted-device randomness expansion • Untrusted-device randomness amplification • Semi-device-independent random number 101011110110001001101100 generation. Small uniform seed + • untrusted device -> uniform randomness 00111011 Randomness extraction Only assumption: Non-communication. 11110110111101111111 1101000010100111111 0101011101010 ….

Results

Timeline Colbeck Us 2006 2007 Colbeck proposed a protocol based on repeating a nonlocal game. 2008 2009 2010 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

Timeline Colbeck Pironio+ Us started 2006 2007 Pironio+: analysis & experiment. I started working in quantum information. 2008 2009 2010 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

The challenge of the entangled adversary Timeline Quantum information can be locked – accessible only to entangled Colbeck [E. g. , Di. Vincenzo+ 04] Pironio+ adversaries. Us started 2006 2007 0 0 2008 0 1 2009 0 1 Pironio+: analysis & experiment. I started working in quantum information. 0 0 1 … 1 1 0 … 2010 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

Timeline Colbeck Pironio+ Us started 2006 2007 Pironio+: analysis & experiment. I started working in quantum information. 2008 2009 2010 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

Timeline Colbeck Pironio+ Fehr+ Us Coudron+ started 2006 2007 2008 Pironio+, Fehr+, Coudron+ proved security against unentangled adversary. Methods: Classical statistical arguments (e. g. , Azuma’s inequality). 2009 2010 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

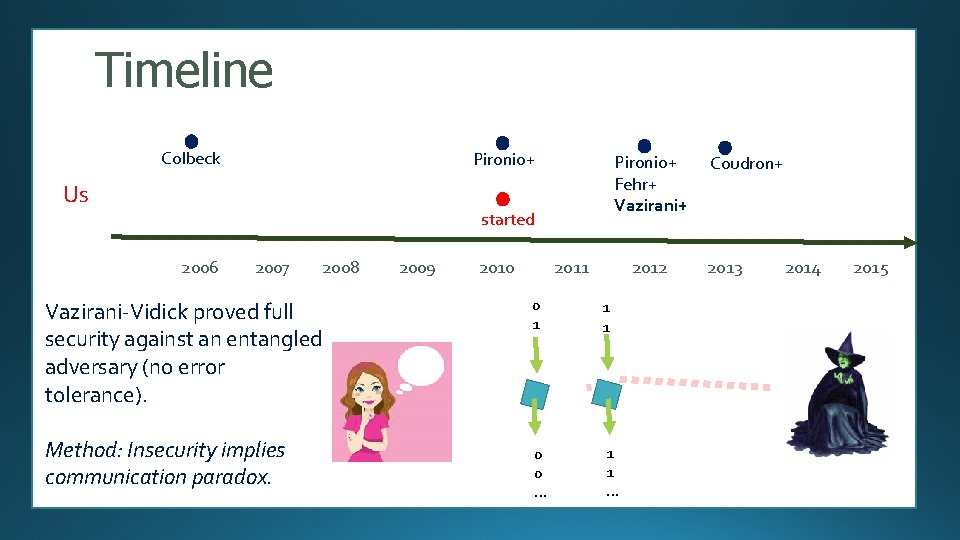
Timeline Colbeck Pironio+ Us Pironio+ Fehr+ Vazirani+ started 2006 2007 2008 Vazirani-Vidick proved full security against an entangled adversary (no error tolerance). Method: Insecurity implies communication paradox. 2009 2010 2011 2012 0 1 1 1 0 0 … 1 1 … Coudron+ 2013 2014 2015

Timeline Colbeck Pironio+ Us Pironio+ Fehr+ Vazirani+ started 2006 2007 We proved full security, with error-tolerance >1. 4%. Method: Constraints on X |-> Tr [ X 1+e] for adversary-output states. 2008 2009 2010 Coudron+ Miller+ 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

Timeline Colbeck Pironio+ Us Pironio+ Fehr+ Vazirani+ started 2006 2007 Coudron+ and Chung+ proved unbounded rate of expansion. 2008 2009 2010 Coudron+ Chung+ Miller+ 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

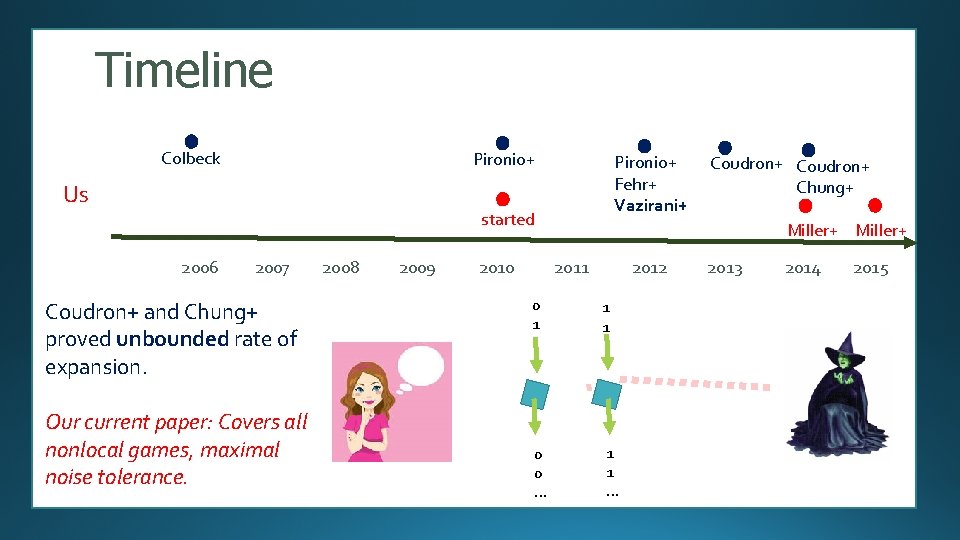
Timeline Colbeck Pironio+ Us Pironio+ Fehr+ Vazirani+ started 2006 2007 Coudron+ and Chung+ proved unbounded rate of expansion. Our current paper: Covers all nonlocal games, maximal noise tolerance. 2008 2009 2010 Coudron+ Chung+ Miller+ 2011 2012 0 1 1 1 0 0 … 1 1 … 2013 2014 2015

Current Result

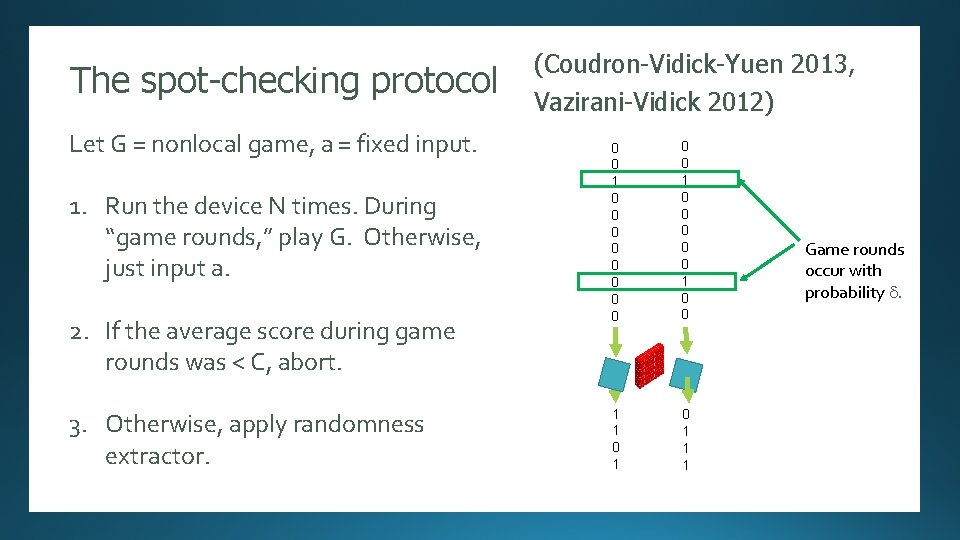
The spot-checking protocol Randomness Expansion (Coudron-Vidick-Yuen 2013, Vazirani-Vidick 2012) Let G = nonlocal game, a = fixed input. 0 0 1 0 0 0 0 0 1 0 0 Small resources, high rate 0 0 Game rounds 0 Not 1 fully secure occur with probability d. 0 0 [Several authors]: Security proof against an unentangled adversary. 1. Run the device N times. During “game rounds, ” play G. Otherwise, just input a. 2. If the average score during game rounds was < C, abort. 1 0 1 11011 1 1…. 10100101110101000101101010001111111010100010 3. Otherwise, apply randomness extractor.

The spot-checking Randomness Expansion (Coudron-Vidick-Yuen 2013, protocol Let WG, a = optimal score among Vazirani-Vidick 2012) devices that are deterministic on a. 0 Let G = nonlocal game, a = fixed input. 0 0 0 [Several authors]: Security proof against an unentangled adversary. 1 Thm (CVY 10 13): The protocol is 0 1. Run the device N times. During 0 0 secure against an Small resources, high rate 0 unentangled 0 “game rounds, ” play G. Otherwise, 0 0 Game rounds adversary if C > W. 0 0 G, a just input a. occur with 2. If the average score during game rounds was < C, abort. 0 0 0 Not 1 fully secure 0 0 Thm (MS 15): The protocol is secure against any adversary if C > WG, a. 1 0 1 11011 1 1…. 10100101110101000101101010001111111010100010 3. Otherwise, apply randomness extractor. probability e. Best possible!

How much randomness (MS 15) Randomness Expansion [Several authors]: Security proof against an unentangled adversary. noise threshold vs. # of random bits per round WG, a WG 11011 10100101110101000101101010001111111010100010 ….

Proof Techniques

ARandomness Mathematical Preliminary Expansion 1+e]. [Several authors]: an unentangled adversary. Consider the function. Security f(X) = Trproof [ |X|against - If X is a density operator, f measures how deterministic X is. (Smaller = more random. ) - f is “almost” a norm on Hermitian operators.

ARandomness Mathematical Preliminary Expansion authors]: Security proof against an [Ball+ unentangled The[Several function Tr [ |X|1+e ] is uniformly convex. 94] adversary. S 11011 10100101110101000101101010001111111010100010 …. (S+T)/2 Gap is (e ). T

ARandomness Mathematical Preliminary Expansion [Several authors]: Security proof against adversary. Consequence [MS 15]: Suppose |-> ’ is an theunentangled result of a binary measurement. 11011 Gap…. = increase 10100101110101000101101010001111111010100010 ’ in randomness. The more disturbance caused by a measurement, the more randomness it adds. Call this the (1+e)-uncertainty principle. U U*

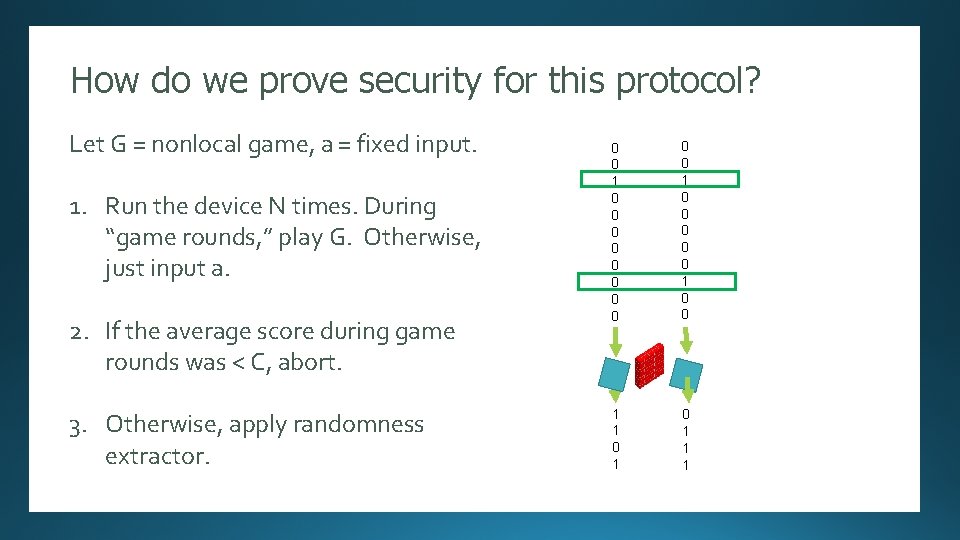
How do we prove security for this protocol? Randomness Expansion Let G = nonlocal game, a = fixed input. 0 0 1 0 0 0 0 0 1 0 0 Small resources, 0 0 0 Not 1 fully secure 0 0 [Several authors]: Security proof against an unentangled adversary. 1. Run the device N times. During “game rounds, ” play G. Otherwise, just input a. 2. If the average score during game rounds was < C, abort. 1 0 1 11011 1 1…. 10100101110101000101101010001111111010100010 3. Otherwise, apply randomness extractor. high rate

How do we prove security for this point: protocol? A starting Randomness Expansion Let G = nonlocal game, a = fixed input. 0 0 is a function Suppose p such that any 0 0 [Several authors]: Security proof against an unentangled adversary. 1 1 device satisfies 0 0 1. Run the device N times. During 0 0 Small resources, high rate 0 0 “game rounds, ” play G. Otherwise, H ( output | input = a) >= 0 0 0 just input a. Not 1 fully p 00(P ( win )) secure 2. If the average score during game rounds was < C, abort. 0 0 Prop (easy): In the non-adversarial IID case, the protocol produces at least p ( C)1 N extractable bits. 0 3. Otherwise, apply randomness 1 1 0 1 extractor. 11011 1 10100101110101000101101010001111111010100010 p = “simple rate 1…. curve”

What about non-IID? Randomness Expansion 1 1+e Compare: [Several authors]: Security proof against an unentangled adversary. * von Neumann entropy (H) * Renyi entropy (H 1+e). H 1+e proves extractable bits in the non-IID case! But it’s hard to relate to the winning probability. P ( win ) 11011 10100101110101000101101010001111111010100010 …. ? !!

What about non-IID? Randomness Expansion 1 1+e Compare: [Several authors]: Security proof against an unentangled adversary. * von Neumann entropy (H) * Renyi entropy (H 1+e). H 1+e proves extractable bits in the non-IID case! But it’s hard to relate to the winning probability. Def: the (1+e)-winning probability of a device is P ( win ) 11011 10100101110101000101101010001111111010100010 …. where r = adversary’s state. P 1+e (win )

What about non-IID? Randomness Expansion 1 1+e Def: [Several p is a strong rate curve for the game on input an unentangled authors]: Security proof. Gagainst adversary. a if for all devices D, H 1+e (output on input a | adversary ) is greater than or equal to p (P 1+e (win )) + Odev. -ind. (e). P ( win ) Thm [MS 15]: If p is a strong rate curve, then the 11011 produces N p (C) extractable spot-checking protocol …. bits. (N = # of rounds, C 10100101110101000101101010001111111010100010 = noise threshold. ) P 1+e (win )

How do we prove strong rate curves? Randomness Expansion Pre-apply the measurement for input a. Want: High P 1+e (win ) implies high Hproof [Several authors]: Security against an unentangled adversary. 1+e. Create a new device by pre-measuring w/ input a. If this brings the score down significantly, then a significant amount of state disturbance has occurred. (1+e)-uncertainty principle says that randomness was generated! So if P 1+e(win) is significantly larger than WG, a, we have randomness. 11011 P 1+e(win) 10100101110101000101101010001111111010100010 …. vs. P 1+e(win) <= WG, a

The universal rate curves Randomness Expansion Thm: Forauthors]: any (G, a)Security the function [Several proof against an unentangled adversary. is a strong rate curve. WG, a Noise tolerance for CHSH game: 10. 3%! 11011 10100101110101000101101010001111111010100010 …. WG

Addendum: DI-QKD

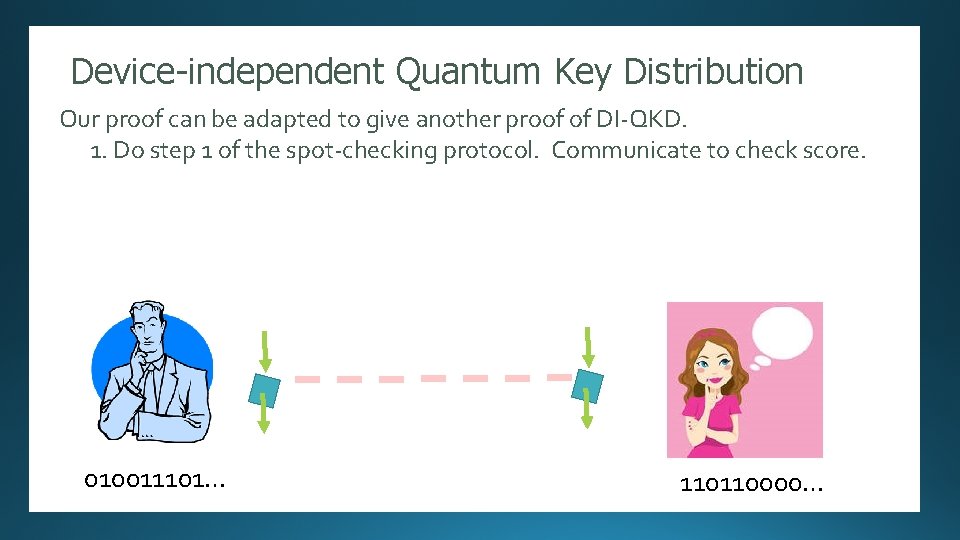
Device-independent Quantum Key Distribution Randomness Expansion Our proof can be adapted to give another proof of DI-QKD. 1. Do stepauthors]: 1 of the spot-checking protocol. to check score. [Several Security proof against. Communicate an unentangled adversary. 010011101… 11011 10100101110101000101101010001111111010100010 …. 110110000…

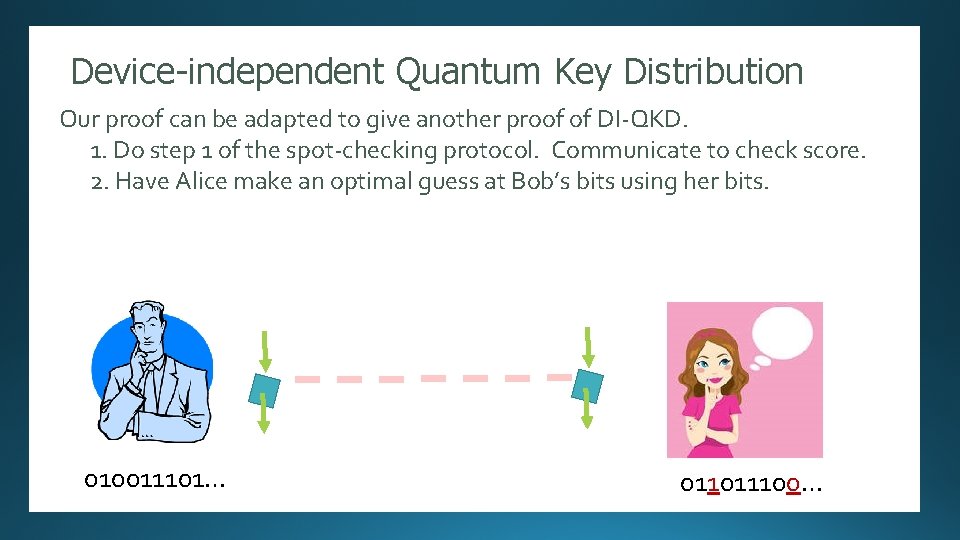
Device-independent Quantum Key Distribution Randomness Expansion Our proof can be adapted to give another proof of DI-QKD. 1. Do stepauthors]: 1 of the spot-checking protocol. to check score. [Several Security proof against. Communicate an unentangled adversary. 2. Have Alice make an optimal guess at Bob’s bits using her bits. 010011101… 11011 10100101110101000101101010001111111010100010 …. 011011100…

Device-independent Quantum Key Distribution Randomness Expansion Our proof can be adapted to give another proof of DI-QKD. 1. Do stepauthors]: 1 of the spot-checking protocol. to check score. [Several Security proof against. Communicate an unentangled adversary. 2. Have Alice make an optimal guess at Bob’s bits using her bits. 3. Perform information reconciliation. 010011101… 11011 10100101110101000101101010001111111010100010 …. 010011101…

Device-independent Quantum Key Distribution Randomness Expansion Our proof can be adapted to give another proof of DI-QKD. 1. Do stepauthors]: 1 of the spot-checking protocol. to check score. [Several Security proof against. Communicate an unentangled adversary. 2. Have Alice make an optimal guess at Bob’s bits using her bits. 3. Perform information reconciliation. 4. Perform randomness extraction. This works if step 1 generates more entropy than is lost at step 3. 11100… 11011 10100101110101000101101010001111111010100010 …. 11100…

Open Problems

Prove the best possible rate curves Randomness Expansion We haveauthors]: two families of rate [Several Security proof against an unentangled adversary. curves, neither optimal. What are the best rate curves? Can we match the classicaladversary rate curves? WG, a 11011 10100101110101000101101010001111111010100010 …. WG

Parallel randomness expansion Randomness Expansion 011010111011010 001001101 01101011 111101 010100101 10101011111 01010 00100000 Give inputs to the Security boxes allproof at against an unentangled adversary. [Several authors]: once. Can we still verify randomness? 0010010 101110101 00001 101111011 010111010 010111 10101000 111110000 010101101 01100000 11011 10100101110101000101101010001111111010100010 ….

Randomness Expansion [Several authors]: Security proof against an unentangled adversary.