The Quantized Free Electron Theory Jellium model Electron

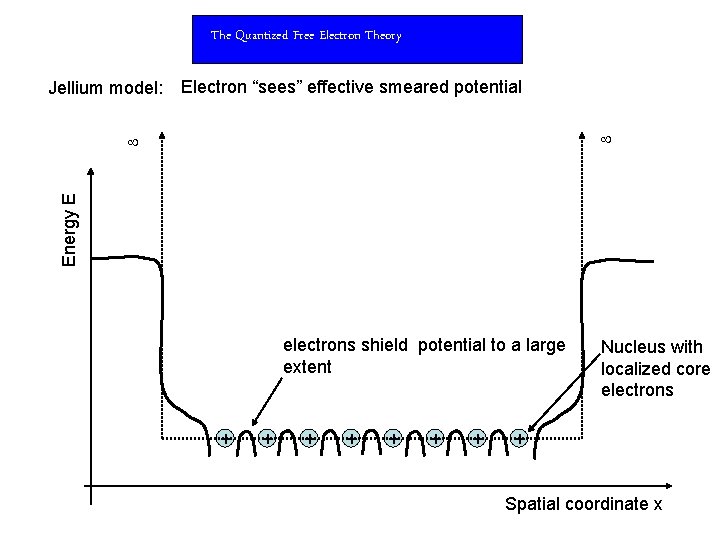
The Quantized Free Electron Theory Jellium model: Electron “sees” effective smeared potential Energy E electrons shield potential to a large extent + + + + Nucleus with localized core electrons + Spatial coordinate x

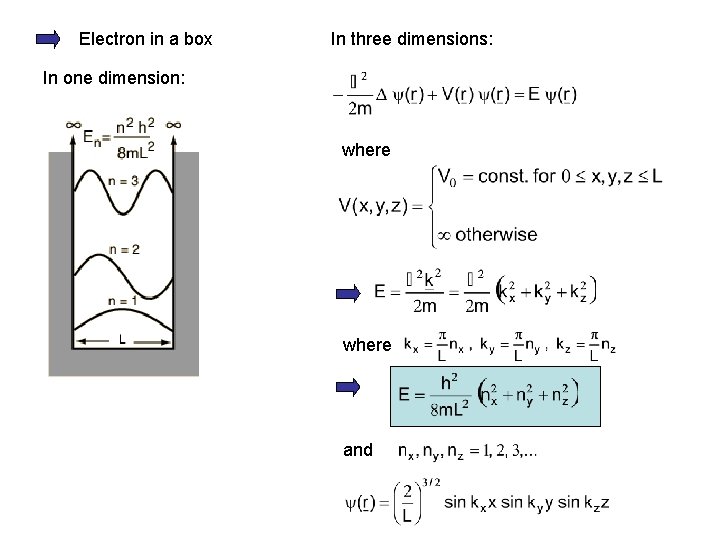
Electron in a box In three dimensions: In one dimension: where and

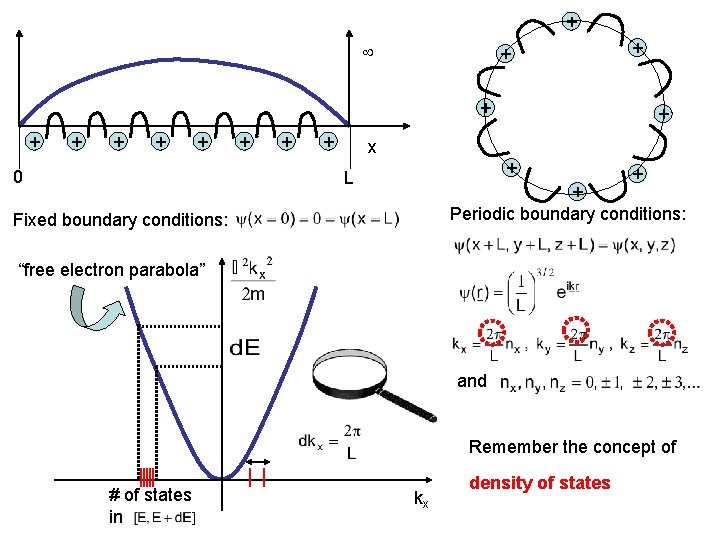
+ + + + + 0 + + x + L + + Periodic boundary conditions: Fixed boundary conditions: “free electron parabola” and Remember the concept of # of states in kx density of states

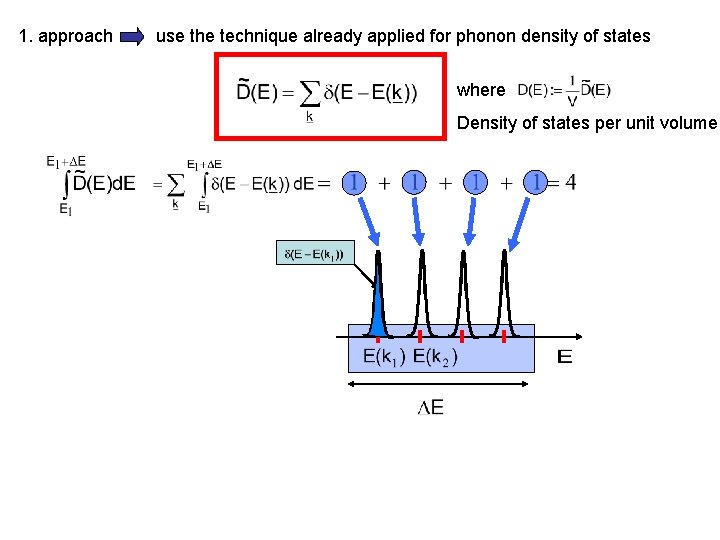
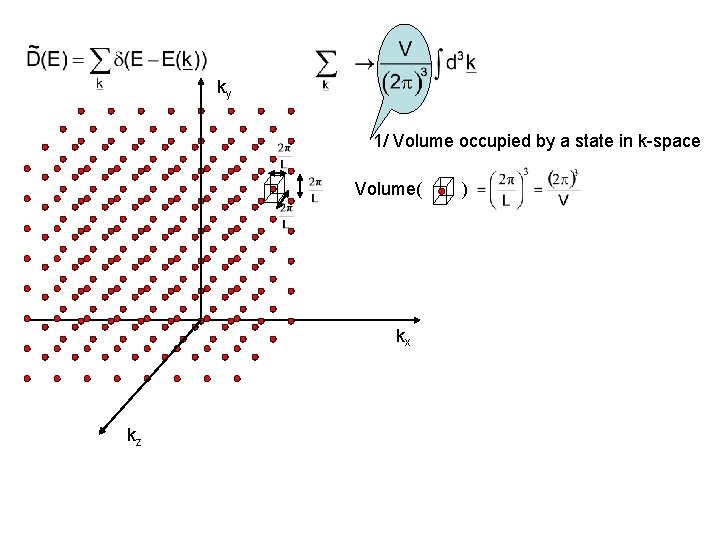
1. approach use the technique already applied for phonon density of states where Density of states per unit volume

ky 1/ Volume occupied by a state in k-space Volume( kx kz )

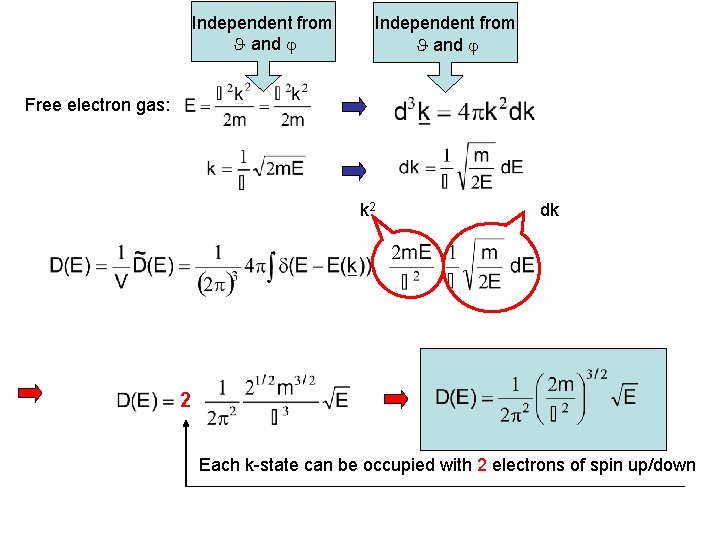
Independent from and Free electron gas: k 2 dk 2 Each k-state can be occupied with 2 electrons of spin up/down

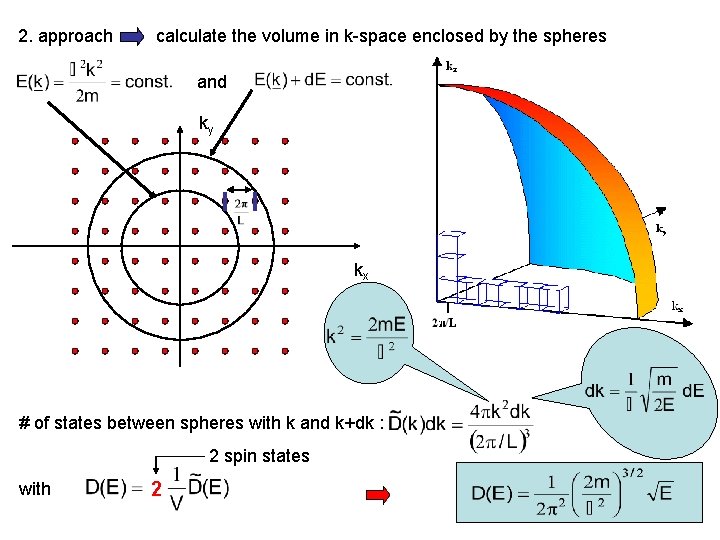
2. approach calculate the volume in k-space enclosed by the spheres and ky kx # of states between spheres with k and k+dk : 2 spin states with 2

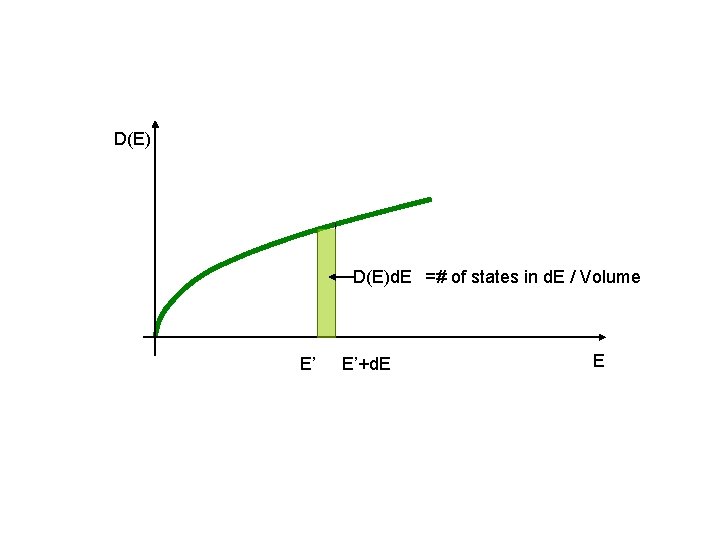
D(E)d. E =# of states in d. E / Volume E’ E’+d. E E

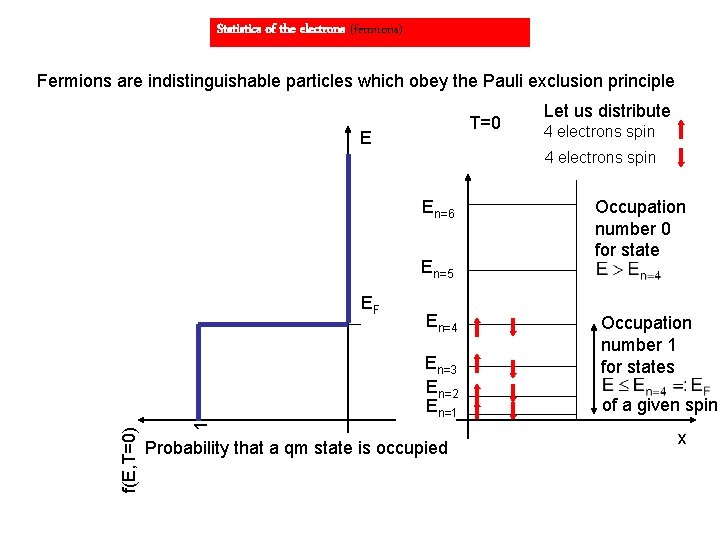
Statistics of the electrons (fermions) Fermions are indistinguishable particles which obey the Pauli exclusion principle T=0 E Let us distribute 4 electrons spin En=6 En=5 EF En=4 1 f(E, T=0) En=3 En=2 En=1 Probability that a qm state is occupied Occupation number 0 for state Occupation number 1 for states of a given spin x

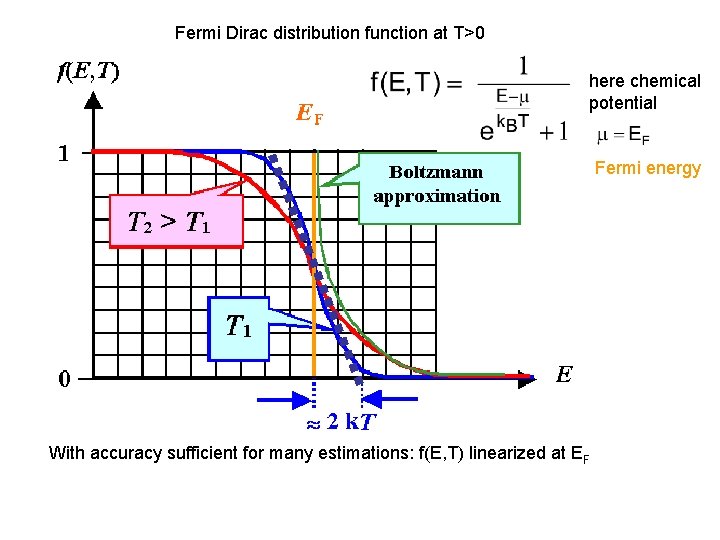
Fermi Dirac distribution function at T>0 here chemical potential Fermi energy With accuracy sufficient for many estimations: f(E, T) linearized at EF

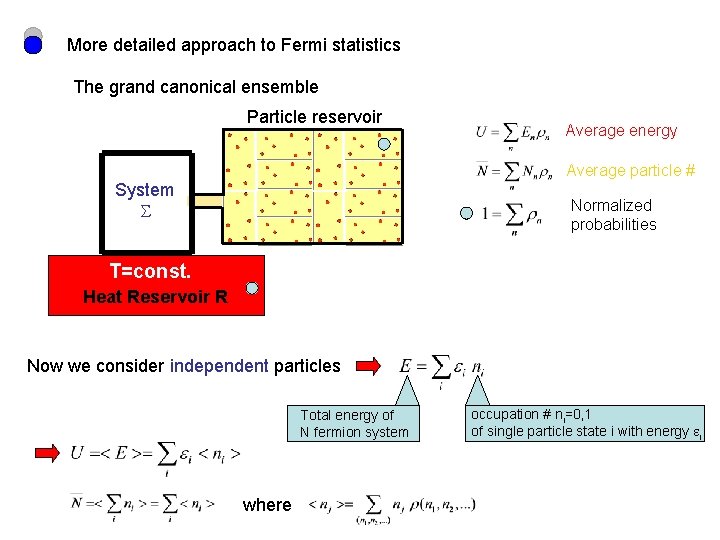
More detailed approach to Fermi statistics The grand canonical ensemble Particle reservoir Average energy Average particle # System Normalized probabilities T=const. Heat Reservoir R Now we consider independent particles Total energy of N fermion system where occupation # ni=0, 1 of single particle state i with energy i

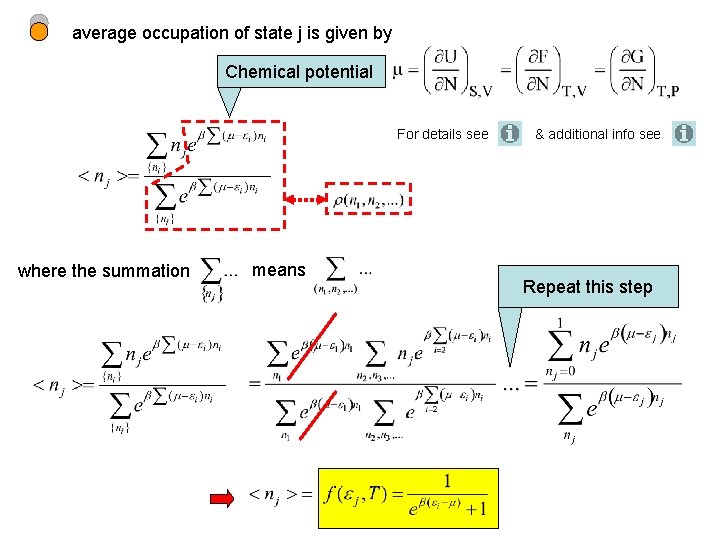
average occupation of state j is given by Chemical potential For details see where the summation means & additional info see Repeat this step

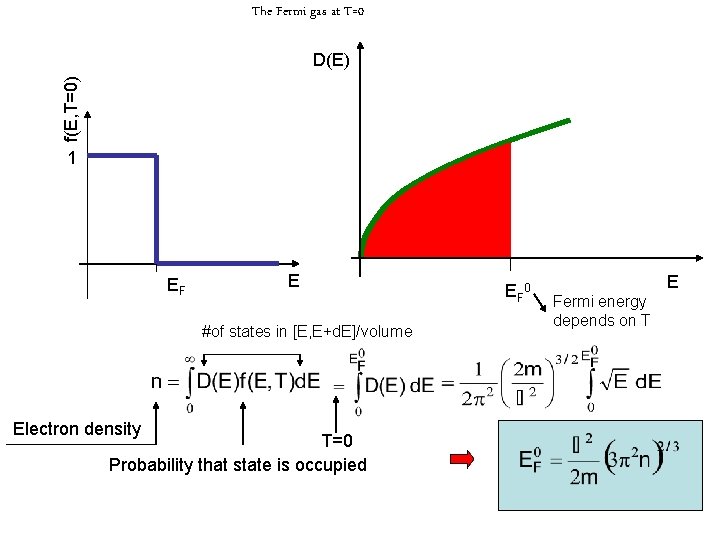
The Fermi gas at T=0 f(E, T=0) D(E) 1 EF E #of states in [E, E+d. E]/volume Electron density T=0 Probability that state is occupied E F 0 E Fermi energy depends on T

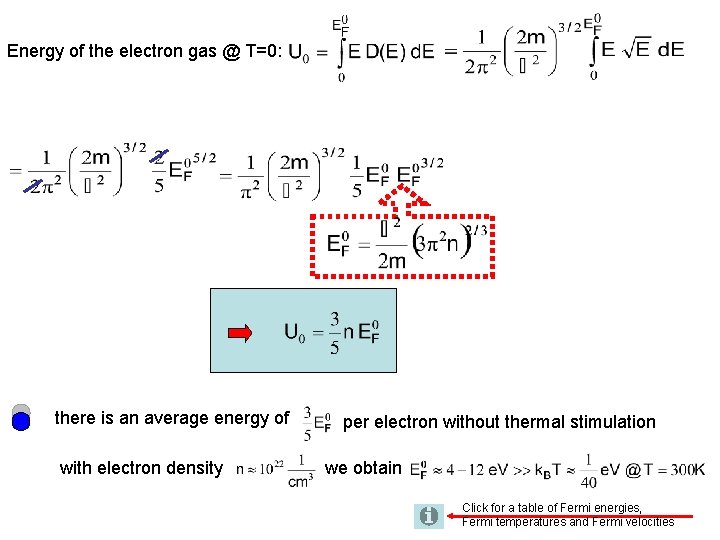
Energy of the electron gas @ T=0: there is an average energy of with electron density per electron without thermal stimulation we obtain Click for a table of Fermi energies, Fermi temperatures and Fermi velocities

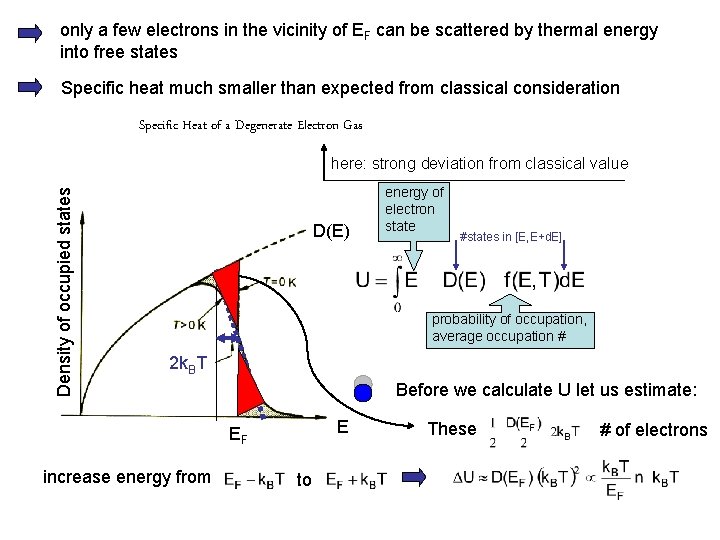
only a few electrons in the vicinity of EF can be scattered by thermal energy into free states Specific heat much smaller than expected from classical consideration Specific Heat of a Degenerate Electron Gas Density of occupied states here: strong deviation from classical value D(E) energy of electron state #states in [E, E+d. E] probability of occupation, average occupation # 2 k. BT Before we calculate U let us estimate: E EF increase energy from to These # of electrons

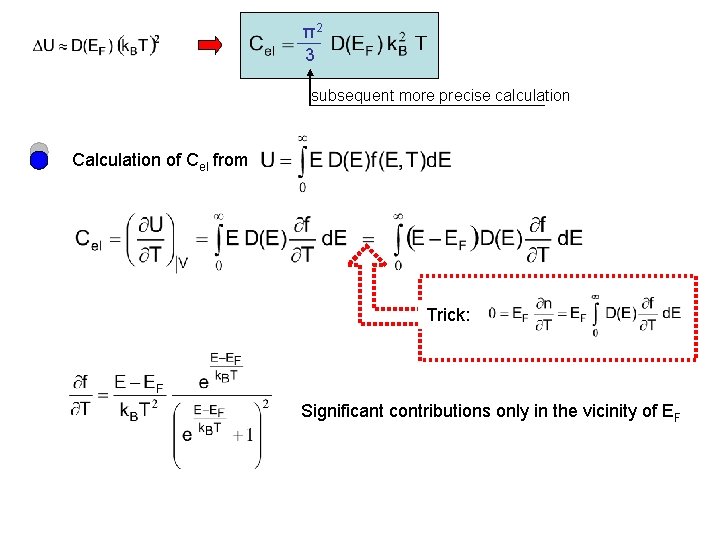
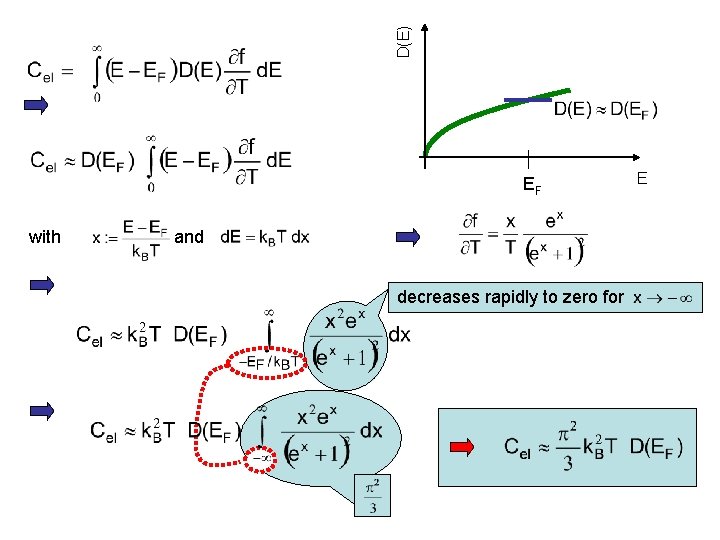
π2 3 subsequent more precise calculation Calculation of Cel from Trick: Significant contributions only in the vicinity of EF

D(E) EF with and decreases rapidly to zero for E

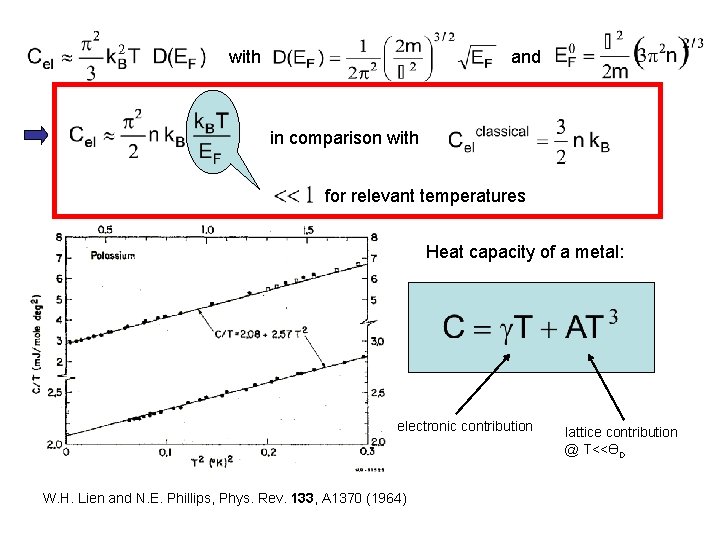
with and in comparison with for relevant temperatures Heat capacity of a metal: electronic contribution W. H. Lien and N. E. Phillips, Phys. Rev. 133, A 1370 (1964) lattice contribution @ T<<ӨD

Selected phenomena which don’t require detailed knowledge of the band structure Temperature dependence of the electrical resistance T Impurities: temperature independent imperfection scattering phonon scattering Scattering of electrons: deviations from a perfect periodic potential Matthiessen’s rule:

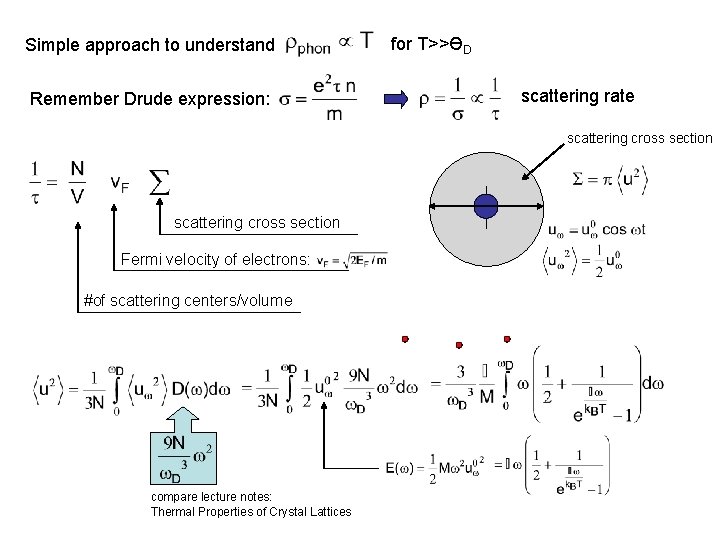
Simple approach to understand Remember Drude expression: for T>>ӨD scattering rate scattering cross section Fermi velocity of electrons: #of scattering centers/volume compare lecture notes: Thermal Properties of Crystal Lattices

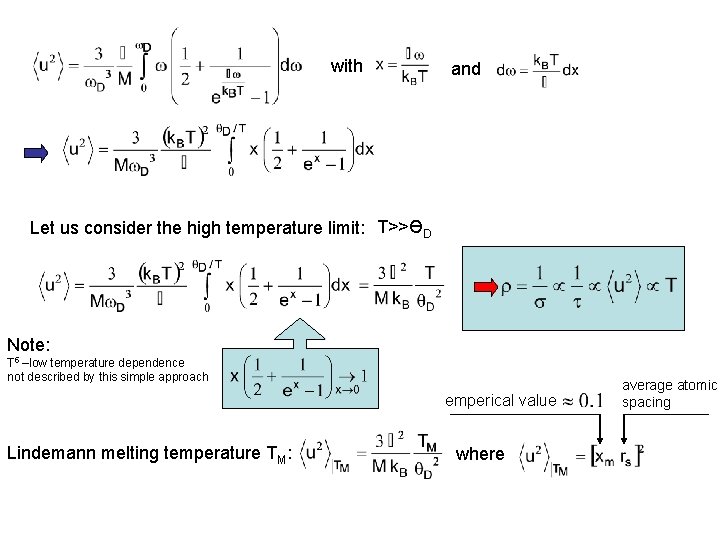
with and Let us consider the high temperature limit: T>>ӨD Note: T 5 –low temperature dependence not described by this simple approach emperical value Lindemann melting temperature TM: where average atomic spacing

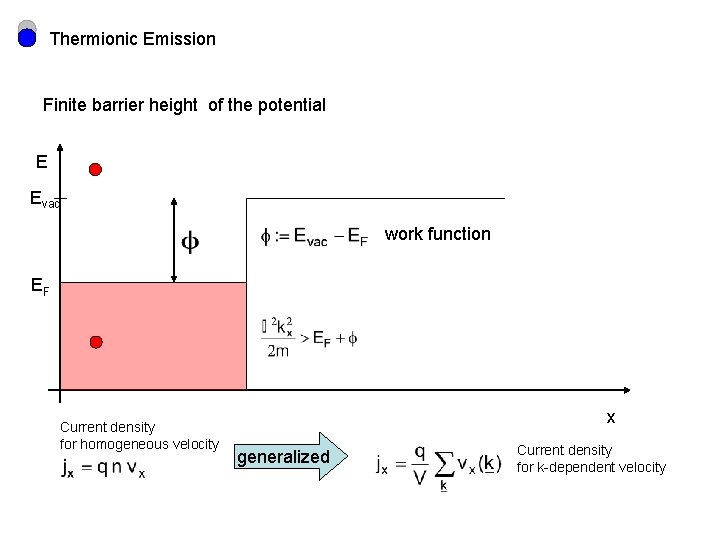
Thermionic Emission Finite barrier height of the potential E Evac work function EF Current density for homogeneous velocity x generalized Current density for k-dependent velocity

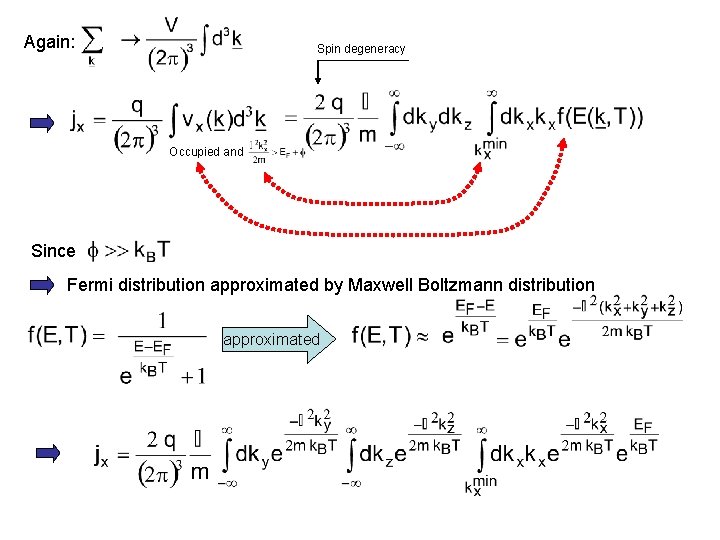
Again: Spin degeneracy Occupied and Since Fermi distribution approximated by Maxwell Boltzmann distribution approximated

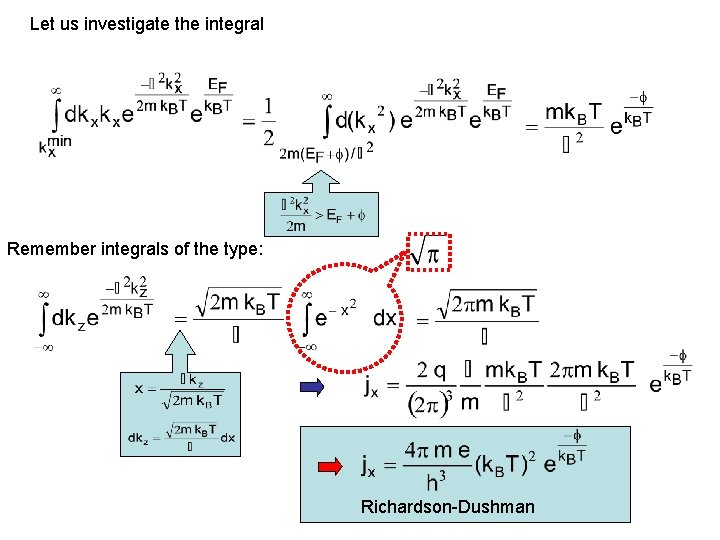
Let us investigate the integral Remember integrals of the type: Richardson-Dushman

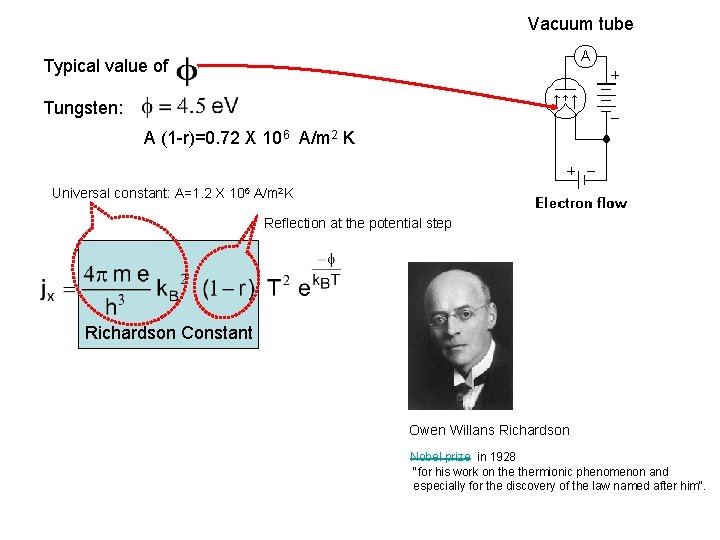
Vacuum tube Typical value of Tungsten: A (1 -r)=0. 72 X 106 A/m 2 K Universal constant: A=1. 2 X 106 A/m 2 K Reflection at the potential step Richardson Constant Owen Willans Richardson Nobel prize in 1928 "for his work on thermionic phenomenon and especially for the discovery of the law named after him".

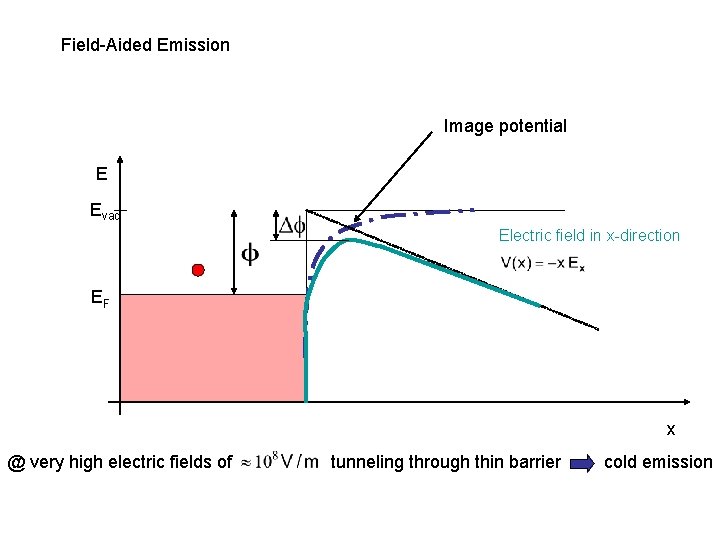
Field-Aided Emission Image potential E Evac Electric field in x-direction EF x @ very high electric fields of tunneling through thin barrier cold emission