The Pythagorean Theorem The Pythagorean Theorem For any














- Slides: 17

The Pythagorean Theorem

The Pythagorean Theorem “For any right triangle, the sum of the areas of the two small squares is equal to the area of the larger. ” a 2 + b 2 = c 2 9/25/2020 2

What is the Pythagorean Theorem used for? • to find the length of a missing side in a right triangle n 5 4

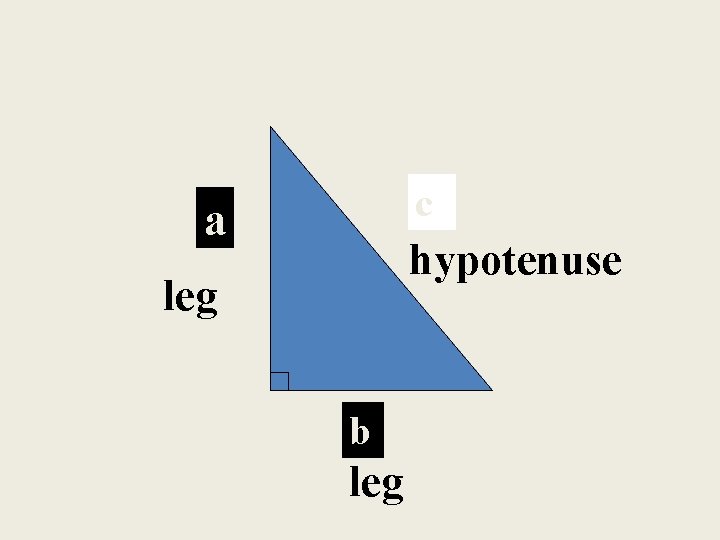
Pythagorean Theorem Formula 2 • a + a and b represent the legs 2 b = 2 c c represents the hypotenuse

c a hypotenuse leg b leg

Important bits of information • The Pythagorean Theorem can only be used on a right triangle. • The legs are always the sides adjacent (next to) the 90 degree angle. • It does not matter which leg is a and which leg is b. • c is always the hypotenuse (the slant)

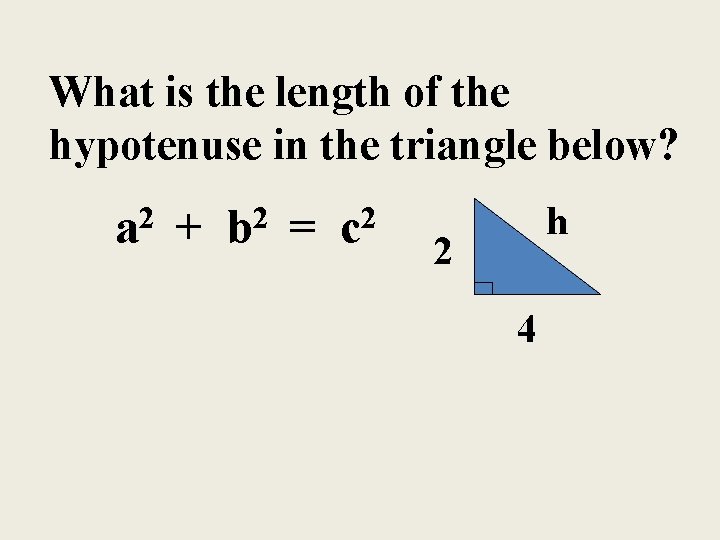
What is the length of the hypotenuse in the triangle below? 2 a + 2 b = 2 c h 2 4

Plug in the value for each variable in the formula.

What is the length of the hypotenuse in the triangle below? h 2 2 a + b = c 2 2 + 2 4 = 2 h 4 + 16 = h 2 20 = h 2 4

What is the length of the hypotenuse in the triangle below? a 2 b 2 + = 22 + 42 = h 2 4 + 16 = h 2 20 = h ~ h 4. 47 ~ c 2 h 2 4

Try this one. . . Find the hypotenuse of the right triangle below? 4 6 h

Find the hypotenuse of the right triangle below? 4 a 2 + b 2 = c 2 42 + 62 = h 2 16 + 36 = h 2 52 = h 7. 21 = h 6 h

Try this one. . . What is the length of the missing leg in the triangle below? 2 a + 2 b = 2 c 5 3 x

Find the hypotenuse of the right triangle below? a 2 + b 2 = c 2 32 + x 2 = 52 9 + x 2 = 25 -9 - 9 x 2 = 16 16 x=4 5 3 x

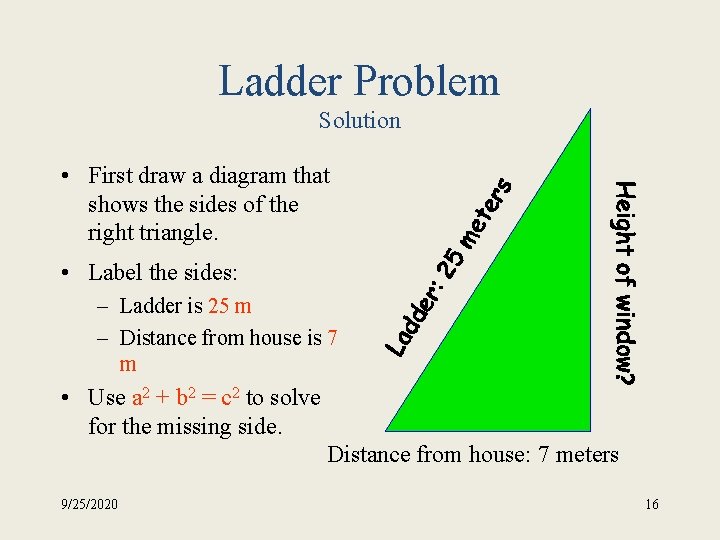
Ladder Problem A ladder leans against a second-story window of a house. If the ladder is 25 meters long, and the base of the ladder is 7 meters from the house, how high is the window? 9/25/2020 15

Ladder Problem Solution • First draw a diagram that shows the sides of the right triangle. • Label the sides: – Ladder is 25 m – Distance from house is 7 m • Use a 2 + b 2 = c 2 to solve for the missing side. Distance from house: 7 meters 9/25/2020 16

Ladder Problem Solution 72 + b 2 = 252 49 + b 2 = 625 b 2 = 576 b = 24 m How did you do? 17