The Pythagorean Theorem Pythagoras abc 2 2 2

The Pythagorean Theorem Pythagoras a+b=c 2 2 2

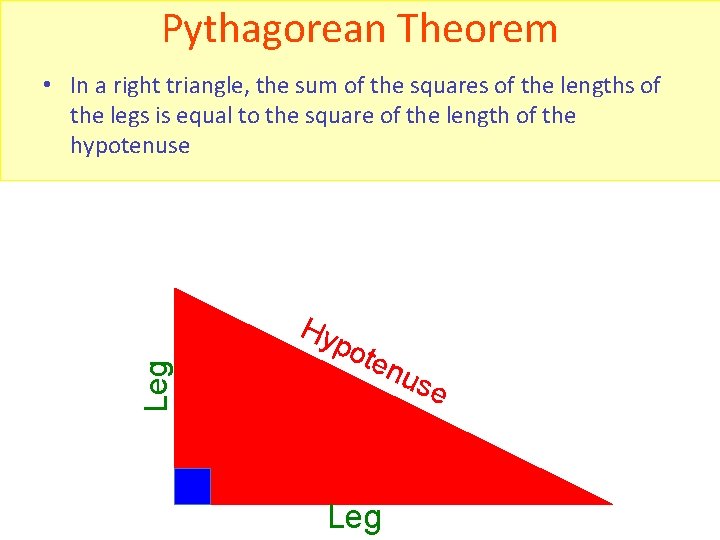
Pythagorean Theorem • In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse Leg Hy pot enu s Leg e

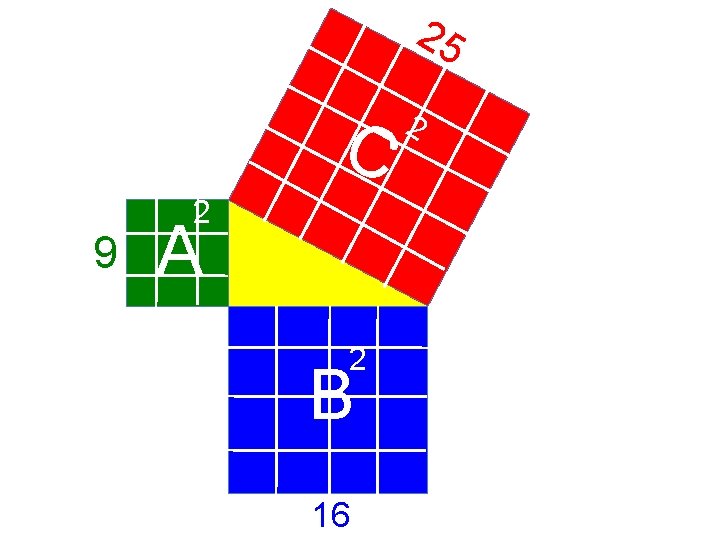
25 C 9 5 22 A 3 4 2 2 2 B 16 2

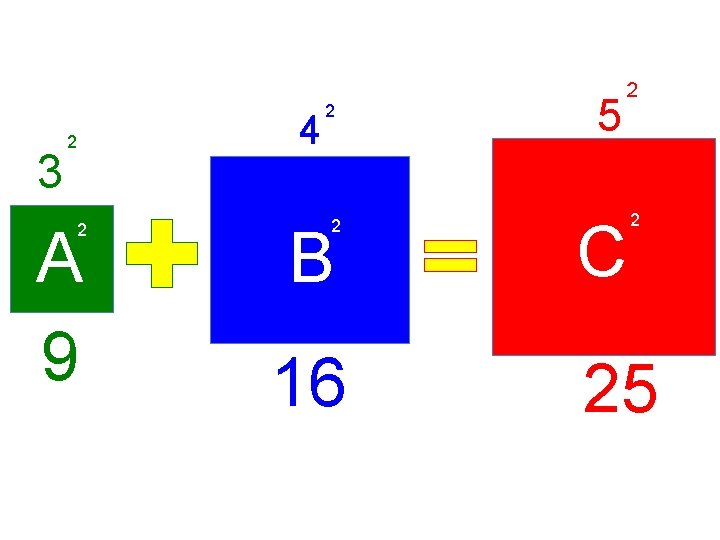
3 2 2 A 9 4 2 5 2 2 B C 16 25 2

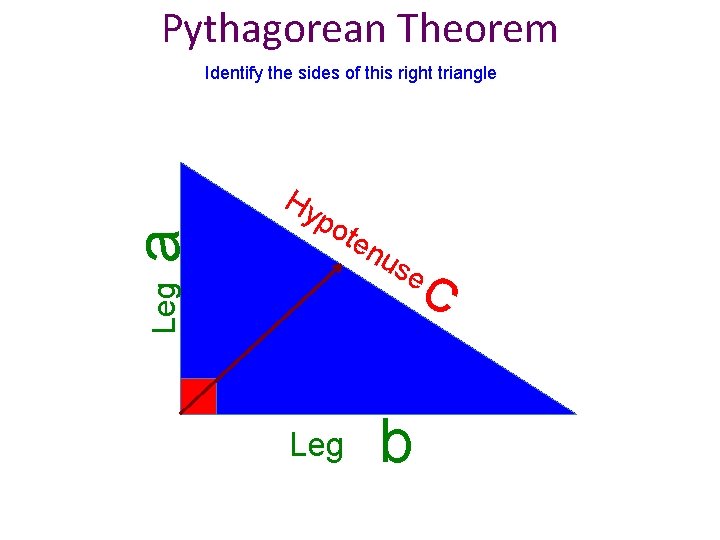
Pythagorean Theorem Leg a Identify the sides of this right triangle Hy po ten us e c Leg b

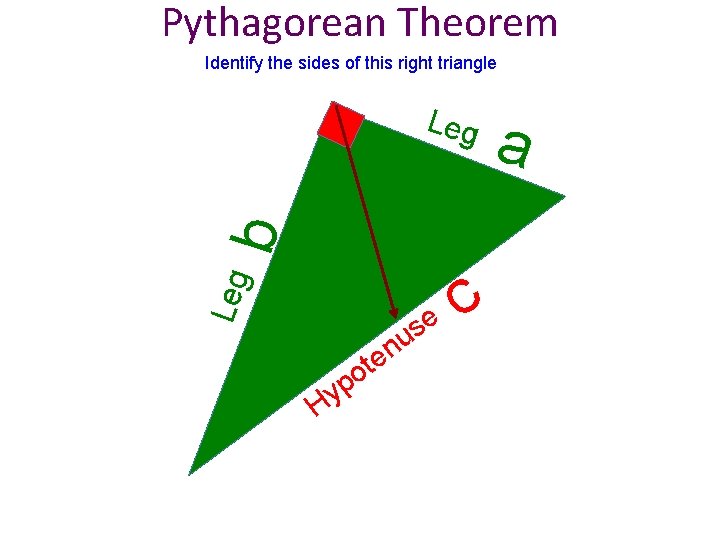
Pythagorean Theorem Identify the sides of this right triangle Leg b Leg se u n e Hy t o p c a

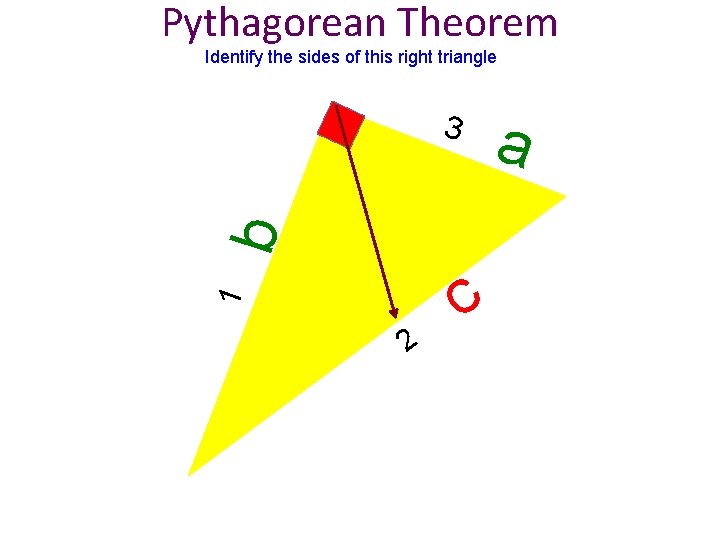
Pythagorean Theorem Identify the sides of this right triangle a 1 b 3 2 c

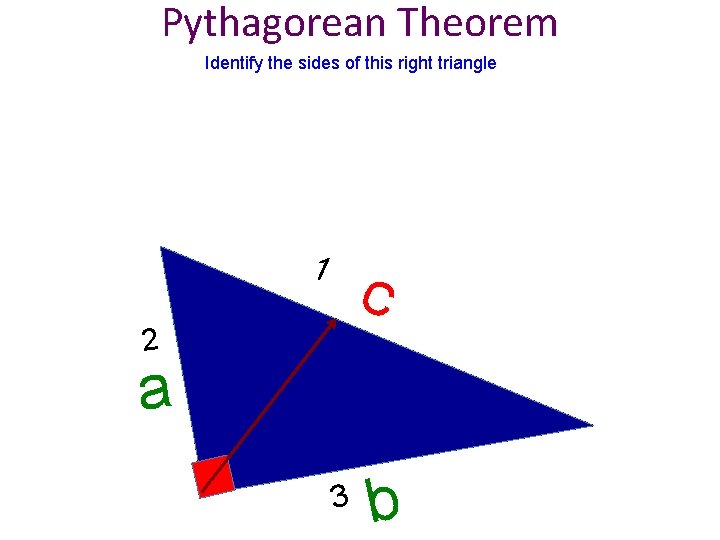
Pythagorean Theorem Identify the sides of this right triangle 1 c 2 a 3 b

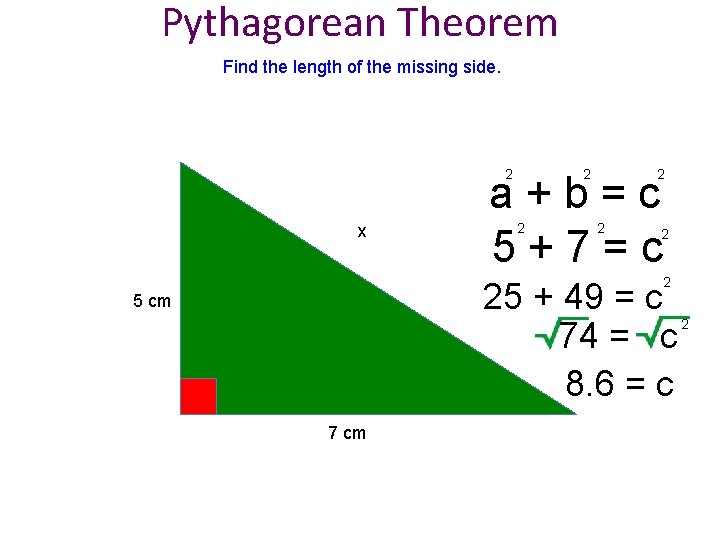
Pythagorean Theorem Find the length of the missing side. 2 2 x 2 a+b=c 5+7=c 2 2 25 + 49 = c 74 = c 8. 6 = c 5 cm 7 cm 2

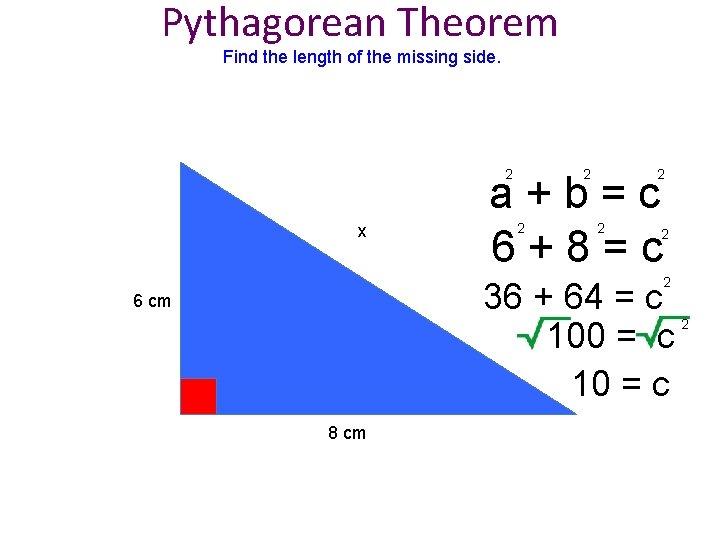
Pythagorean Theorem Find the length of the missing side. 2 2 x 2 a+b=c 6+8=c 2 2 36 + 64 = c 100 = c 10 = c 6 cm 8 cm 2

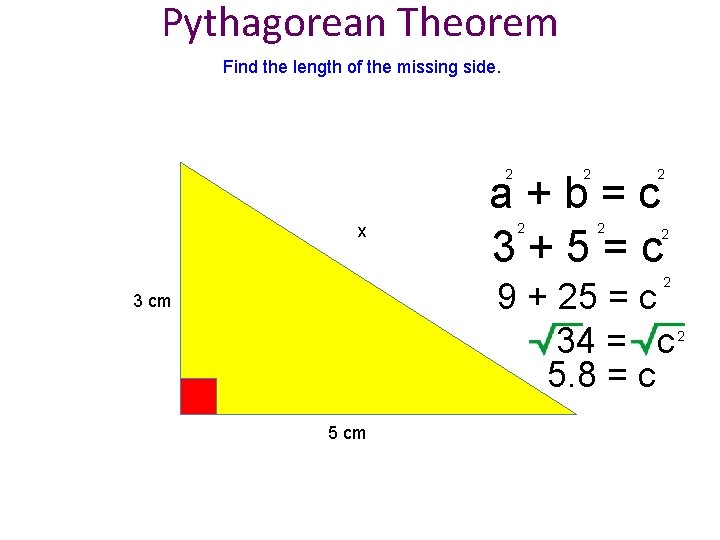
Pythagorean Theorem Find the length of the missing side. 2 2 x 2 a+b=c 3+5=c 2 2 9 + 25 = c 34 = c 5. 8 = c 3 cm 5 cm 2

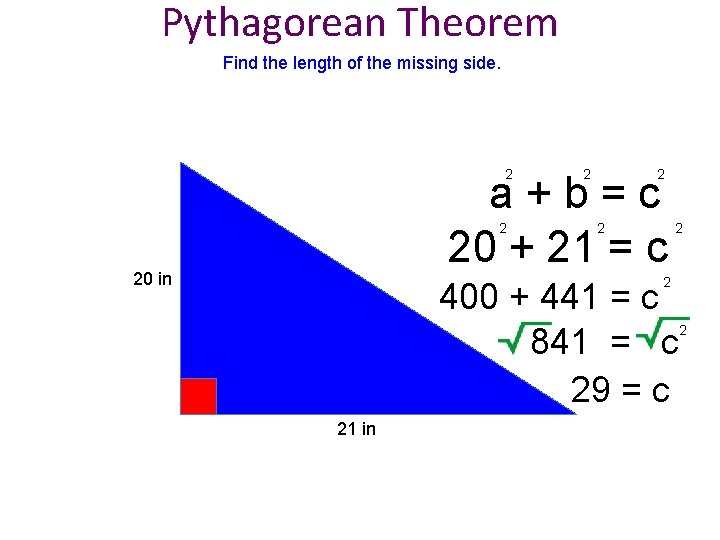
Pythagorean Theorem Find the length of the missing side. 2 2 2 a+b=c 20 + 21 = c 2 20 in 2 2 2 400 + 441 = c 841 = c 29 = c 21 in 2

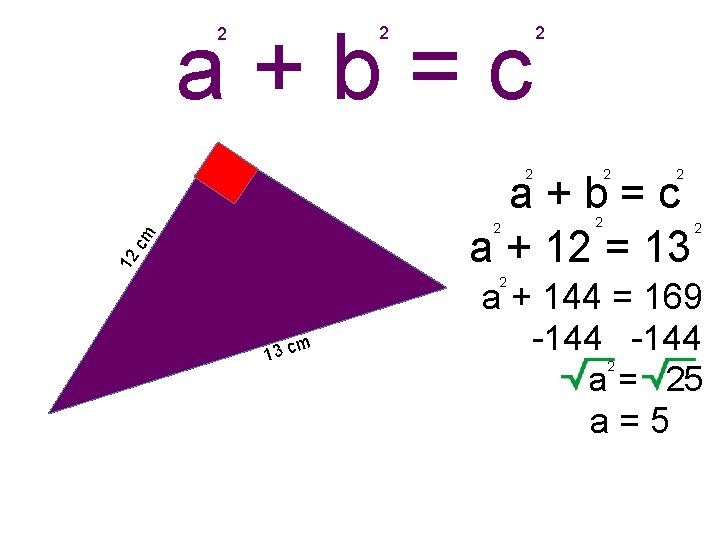
a+b=c 2 2 2 a+b=c a + 12 = 13 12 cm 2 2 m 13 c a + 144 = 169 -144 2 a = 25 a=5

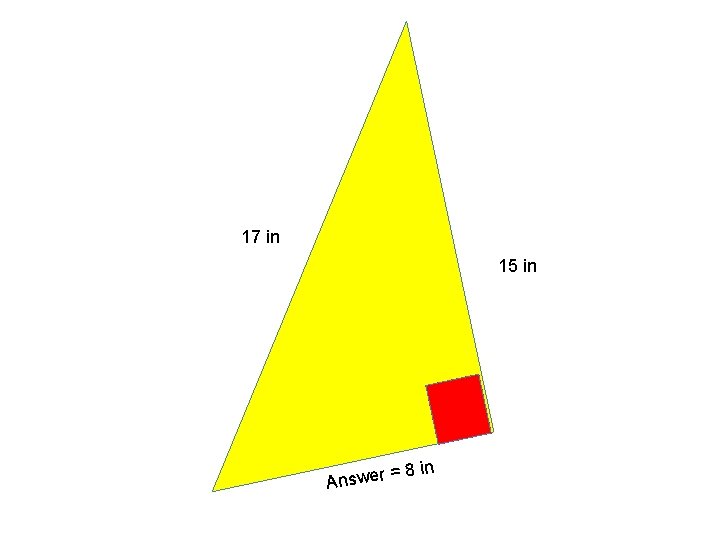
17 in 15 in = Answer 8 in

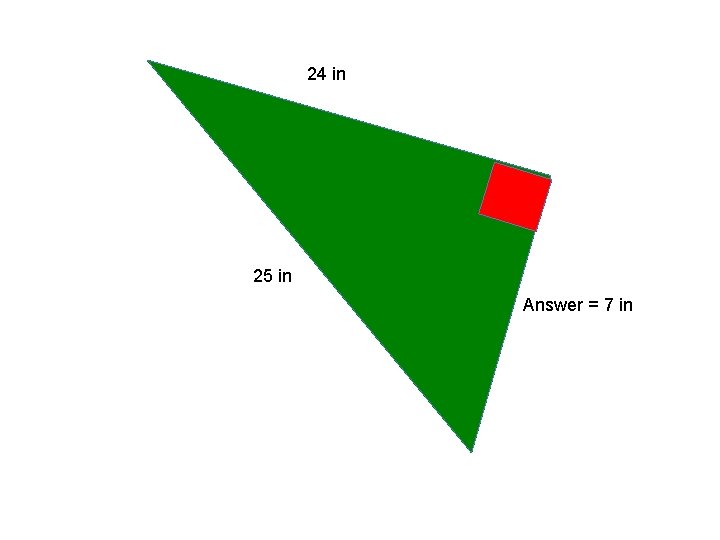
24 in 25 in Answer = 7 in

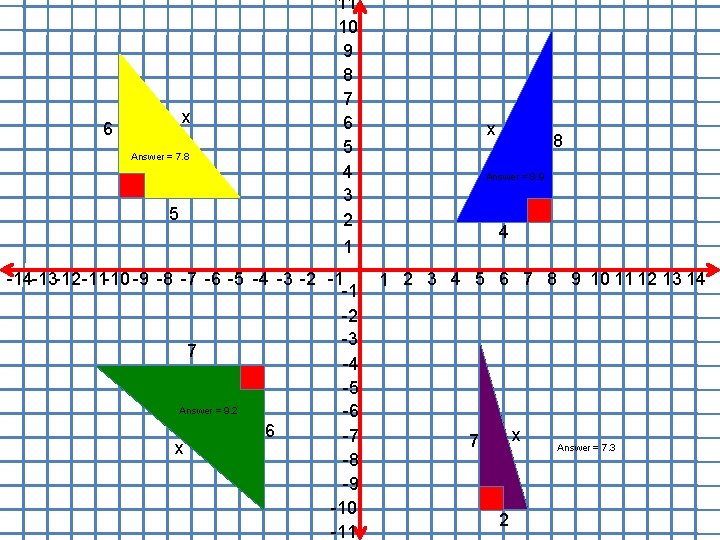
x 6 Answer = 7. 8 5 11 10 9 8 7 6 5 4 3 2 1 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 -1 -2 -3 7 -4 -5 Answer = 9. 2 -6 6 -7 x -8 -9 -10 -11 x 8 Answer = 8. 9 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 x 7 2 Answer = 7. 3

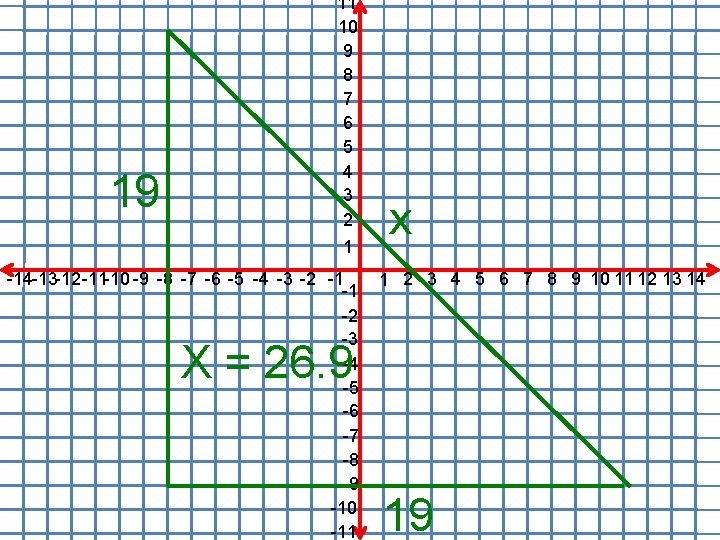
19 11 10 9 8 7 6 5 4 3 2 1 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 X = 26. 9 19

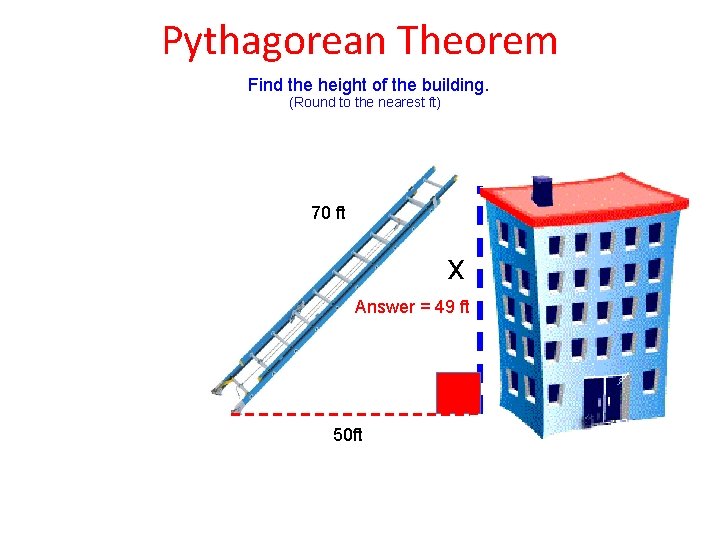
Pythagorean Theorem Find the height of the building. (Round to the nearest ft) 70 ft x Answer = 49 ft 50 ft

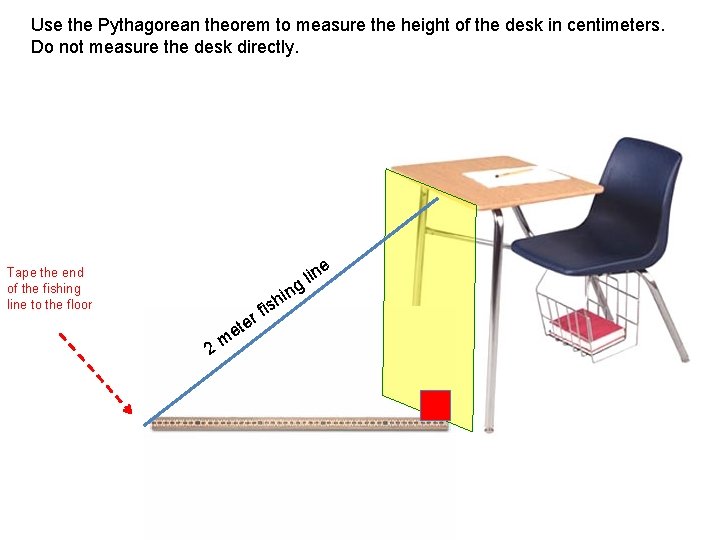
Use the Pythagorean theorem to measure the height of the desk in centimeters. Do not measure the desk directly. Tape the end of the fishing line to the floor ine l g r e t e m 2 in h fis Measure this distance in cm

Converse of the Pythagorean Theorem • If the square of the length of one side of a triangle is equal to the sum of the squares of the length of the other two sides, then the triangle is a right triangle. 2 2 a+ b 3+ 4 9 + 16 25 2 =c =5 = 25 2

Identify a Right Triangle • The measure of three sides of a triangle are 5 inches, 12 inches, and 13 inches. Determine whether the triangle is a right triangle. 2 2 2 a+ b =c 2 2 2 5 + 12 = 13 25 + 144 = 169

Identify a Right Triangle • The measure of three sides of a triangle are 8 inches, 10 inches, and 15 inches. Determine whether the triangle is a right triangle. 2 2 2 a+ b =c 2 2 2 8 + 10 = 15 64 + 100 = 225 164 = 225

Identifying an Obtuse Triangle • If the square of the length of the longest side of a triangle is greater than the sum of the squares of the lengths of the other two sides, the triangle is obtuse 2 2 a+ b 2+ 3 4+ 9 13 < < c 4 16 16 2 2

Identifying an Acute Triangle • If the square of the length of the longest side of a triangle is less than the sum of the squares of the lengths of the other two sides, the triangle is acute. a+ b > c 6 + 7 >8 36 + 49 > 64 85 > 64 2 2 2

Pythagorean triple • Is a set of nonzero whole numbers a, b, and c that satisfy the equation a 2 + b 2 = c 2 Here are some common Pythagorean triples 7, 24, 25 3, 4, 5 5, 12, 13 8, 15, 17