The Propagation Of Mesoscale Convective Complexes The Corfidi

The Propagation Of Mesoscale Convective Complexes The Corfidi Vector Method Mike Peluso Howard Manges 20 April 2006

Corfi. . What? • Corfidi Vectors are a tool that operational meteorologists can use that MAY help more accurately predict: – the motion of MCS’s • More specifically the meso beta convective elements (MBE) – heavy rain – flash flooding – damaging winds What do these vectors represent?

The “Original” Corfidi Method • Sum of two vectors: – Advective – The mean flow of the 850300 mb cloud-layer wind Newton and Katz(1958) and Chappell (1986) – Propagation – Represents new cell formation opposite in direction to the low-level jet but equal in magnitude Merritt and Fritsch, Corfidi et. al (1996)

Advective Component • Simplified example of vertical wind profile through mean cloud layer. • Mean flow vector would be 270°/30 kts 300 -h. Pa 500 -h. Pa 700 -h. Pa • Mathematically: (Vcl) (V 850+V 700+V 500+V 300 )/4 850 -h. Pa

Propagation Component • Represents new cell formation opposite in direction to the low-level jet but equal in magnitude • LLJ 240°/30 kts 850 -h. Pa wind barb • Therefore the vector representative of propagation will be from 60°/30 kts

Addendum to Corfidi Vector Method • A major shortcoming was found in this method. • MCS propagation is not as straight forward as 2 vectors being added or subtracted. • Case studies indicate that the cold pool spatial relationship to the low level inflow (LLJ) has an additional effect on propagation patterns. Thus….

Cold Pool Component • Assuming that new cell development (propagation) is ALWAYS opposite the LLJ is incorrect. • The effect of this spatial relationship of the meso-high to the inflow (LLJ) plays a major role in new cell development – Cumulogenesis occurs along the leading edge of the cold pool and hence the region of greatest LLC Corfidi, WAF (2003)

Cold Pool Component Corfidi et. al (2003)

Modes of MCS Propagation • Two Types • Quasi-stationary – a. k. a back-building or upwind propagating – Significant flood threat • Progressive – a. k. a. forward or downwind propagating – Reduced threat of flooding • Schematically……

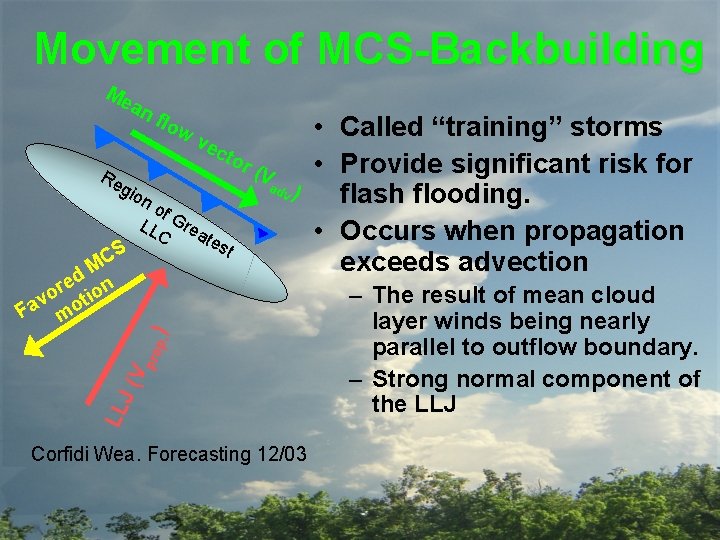
Movement of MCS-Backbuilding Me an flo w cto r Re gio n MCS of p. ) pro (V (V ad d e r o Fav otion m LLJ 300 -h. Pa ve Gr ea v) tes 500 -h. Pa t. L LC 700 -h. Pa 850 -h. Pa • Region of greatest LLC dictates MCS motion. • Assuming sufficient instability and favorable thermodynamic environment Corfidi (2003)

Movement of MCS-Backbuilding Me an Re flo wv ec tor gio ad ) v t LL J( V pro p. ) S C M d re ion o t v Fa m o no f LL Grea C tes (V Corfidi Wea. Forecasting 12/03 • Called “training” storms • Provide significant risk for flash flooding. • Occurs when propagation exceeds advection – The result of mean cloud layer winds being nearly parallel to outflow boundary. – Strong normal component of the LLJ

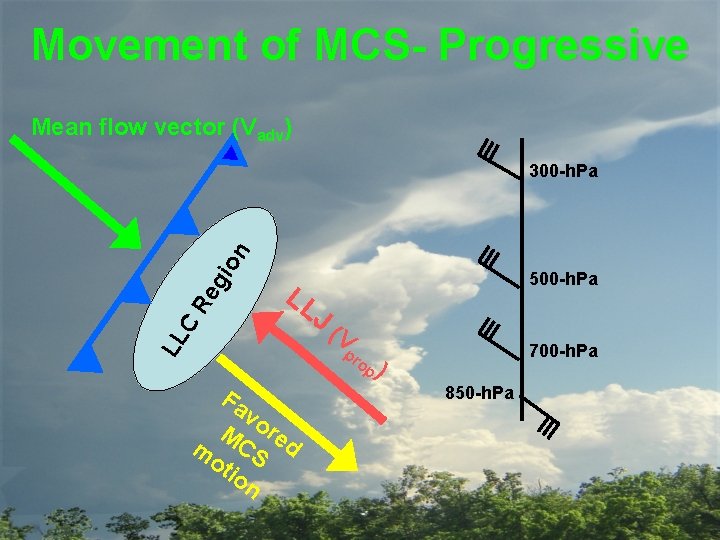
Movement of MCS- Progressive Mean flow vector (Vadv) LL LL C Re gi on 300 -h. Pa 500 -h. Pa J (V 700 -h. Pa pr op ) Fa vo M re m CS d ot io n 850 -h. Pa

Movement of MCS-Progressive Re g io n Mean flow vector (Vadv) LL LL C • Storm motion is opposite the LLJ along the downwind side of cold pool. • Vector length is directly related to rate of cumulogenesis along gust front. • Not usually associated with heavy rainfall or flooding. J (V pr M C ot S io n m op )

Forecast Magnitude of MBE motion • A straight forward calculation can be utilized to determine the magnitude of motion for the MBE (Mesoscale Beta Element). • |VMBE| = { |Vcl|2 + |-VLLJ|2 -2( |Vcl|. |-VLLJ| ) cos Φ}1/2 • Φ = angle between mean cloud layer flow and LLJ

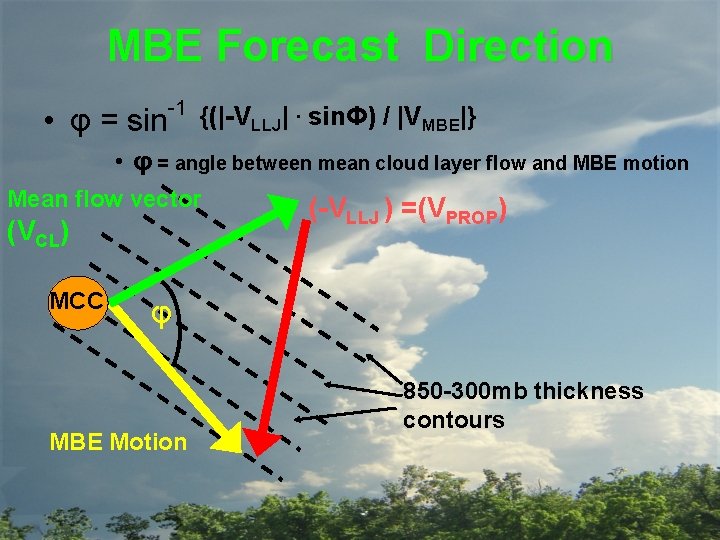
MBE Forecast Direction • φ = sin -1 {(|-VLLJ|. sinΦ) / |VMBE|} • φ = angle between mean cloud layer flow and MBE motion Mean flow vector (VCL) MCC (-VLLJ ) =(VPROP) φ MBE Motion 850 -300 mb thickness contours

The Role of Dry Air • Dry air allows for: – increased evaporative cooling – Sublimation and melting • These create density differences and stronger DD’s • Strong cold pools demonstrate the potential for favoring progressive MCS movement • Weak cold pools favor Quasi-stationary or Backbuilding MCS’s that occur in moist or nearly saturated low-level environments.

Summary • 3 factors influencing motion: – Advective component – Propagation component – Cold pool (outflow boundary). • The spatial relationship between them influences MCS motion • 2 propagation modes: – Upwind or Backbuilding – Downwind or Progressive • Distinguished by orientation of the gust front to the mean wind and the LLJ. • 1 grade A+

References • Corfidi, Stephen F. , 2003: Cold Pools and MCS Propagation: Forecasting the Motion of Downwind-Developing MCS’s. Wea. Forecasting. , 18, 997 -1017. • Merritt, J. H. and Fritsch, J. M. , 1994: Predicting the Movement of Mesoscale Convective Complexes. Wea. Forecasting. , 11, 41 -46. • Corfidi, Stephen F. , 1998: Forecasting MCS Mode and Motion. Prepared for the 19 th Conference Severe Local Storms, Minneapolis, MN 1998.