The Production Process and Costs Production Analysis Production

The Production Process and Costs

Production Analysis • Production Function Q = f(K, L) • Describes available technology and feasible means of converting inputs into maximum level of output, assuming efficient utilization of inputs: • ensure firm operates on production function (incentives for workers to put max effort) • use cost minimizing input mix • Short-Run vs. Long-Run (increases with capital intensity) • Fixed vs. Variable Inputs

Total Product • Cobb-Douglas Production Function • Example: Q = f(K, L) = K. 5 L. 5 • K is fixed at 16 units. • Short run production function: Q = (16). 5 L. 5 = 4 L. 5 • Production when 100 units of labor are used? Q = 4 (100). 5 = 4(10) = 40 units

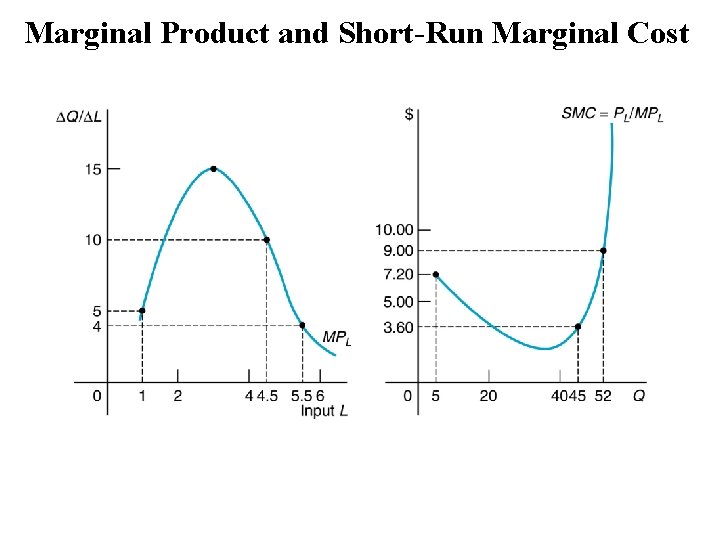
Marginal Product of Labor • Continuous case: MPL = d. Q/d. L • Discrete case: arc MPL = Q/ L • Measures the output produced by the last worker. • Slope of the production function

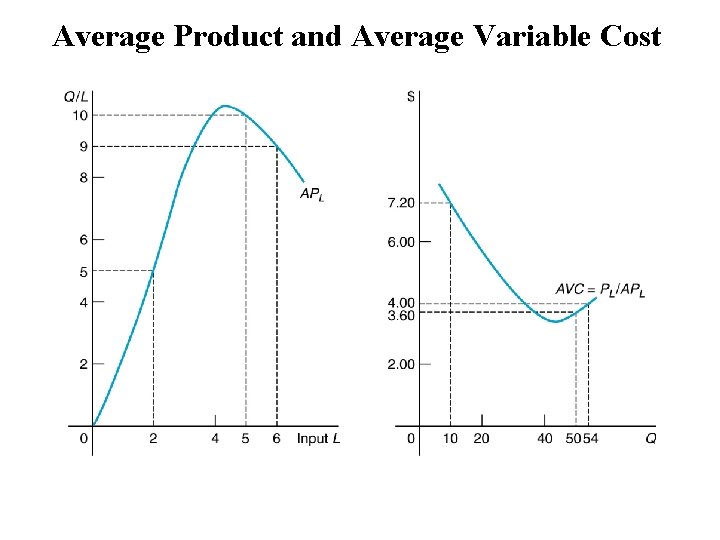
Average Product of Labor • APL = Q/L • Measures the output of an “average” worker. • Slope of the line from origin onto the production function

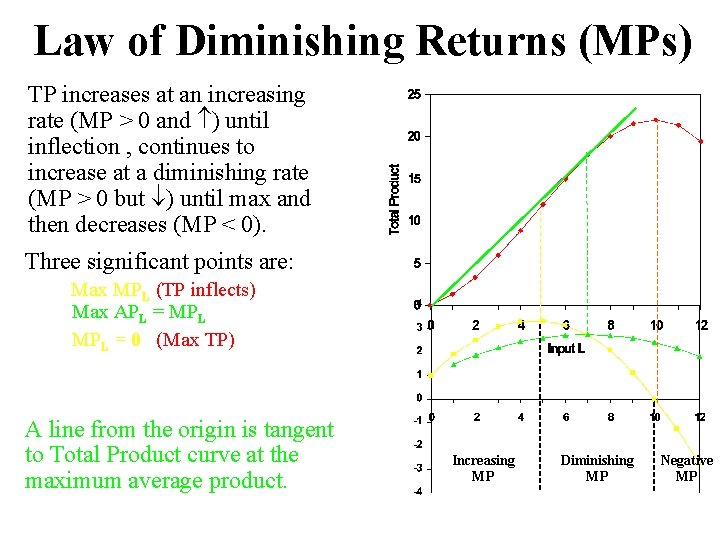
Law of Diminishing Returns (MPs) TP increases at an increasing rate (MP > 0 and ) until inflection , continues to increase at a diminishing rate (MP > 0 but ) until max and then decreases (MP < 0). Three significant points are: Max MPL (TP inflects) Max APL = MPL = 0 (Max TP) A line from the origin is tangent to Total Product curve at the maximum average product. Increasing MP Diminishing MP Negative MP

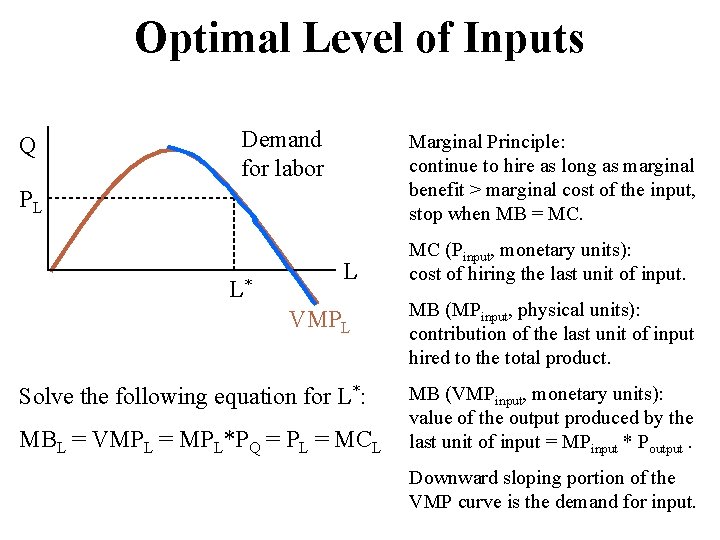
Optimal Level of Inputs Q Demand for labor Marginal Principle: continue to hire as long as marginal benefit > marginal cost of the input, stop when MB = MC. PL L* L VMPL Solve the following equation for L*: MBL = VMPL = MPL*PQ = PL = MCL MC (Pinput, monetary units): cost of hiring the last unit of input. MB (MPinput, physical units): contribution of the last unit of input hired to the total product. MB (VMPinput, monetary units): value of the output produced by the last unit of input = MPinput * Poutput. Downward sloping portion of the VMP curve is the demand for input.

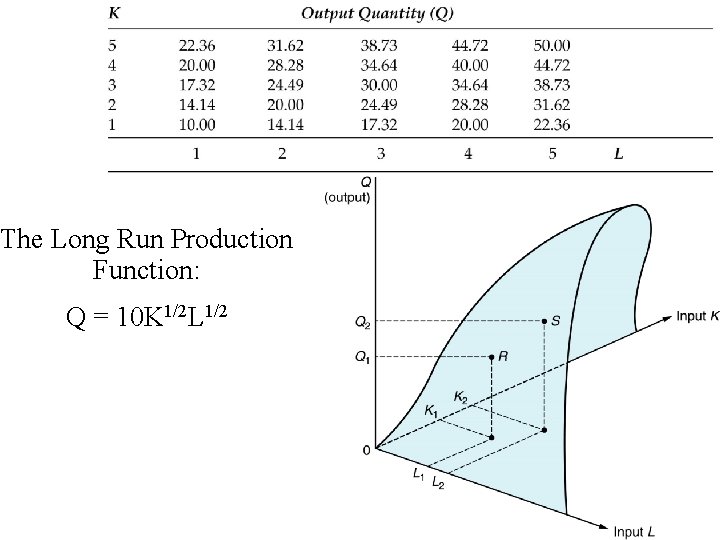
The Long Run Production Function: Q = 10 K 1/2 L 1/2

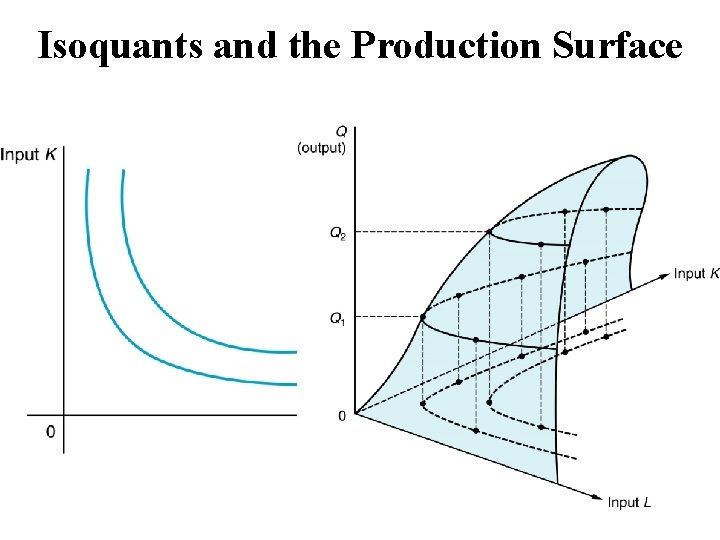
Isoquants and the Production Surface

Isoquant • The combinations of inputs (K, L) that yield the producer the same level of output. • The shape of an isoquant reflects the ease with which a producer can substitute among inputs while maintaining the same level of output. • Slope or Marginal Rate of Technical Substitution can be derived using total differential of Q=f(K, L) set equal to zero (no change in Q along an isoquant)

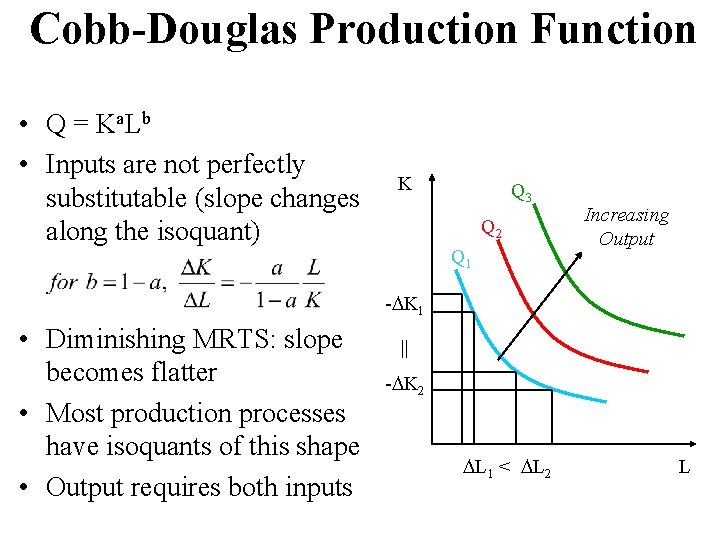
Cobb-Douglas Production Function • Q = K a. L b • Inputs are not perfectly substitutable (slope changes along the isoquant) K Q 3 Q 2 Q 1 Increasing Output - K 1 • Diminishing MRTS: slope becomes flatter • Most production processes have isoquants of this shape • Output requires both inputs || - K 2 L 1 < L 2 L

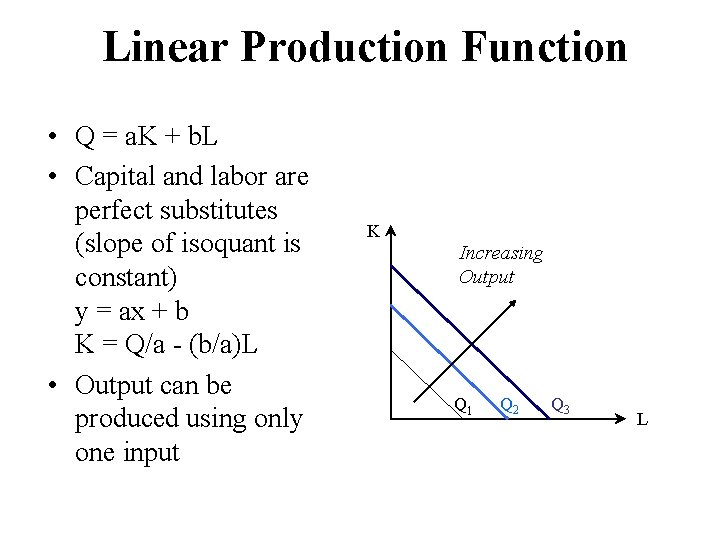
Linear Production Function • Q = a. K + b. L • Capital and labor are perfect substitutes (slope of isoquant is constant) y = ax + b K = Q/a - (b/a)L • Output can be produced using only one input K Increasing Output Q 1 Q 2 Q 3 L

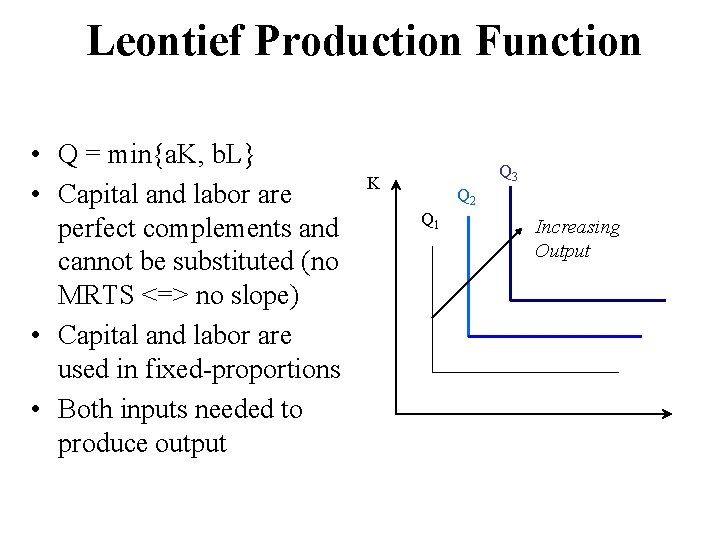
Leontief Production Function • Q = min{a. K, b. L} • Capital and labor are perfect complements and cannot be substituted (no MRTS <=> no slope) • Capital and labor are used in fixed-proportions • Both inputs needed to produce output Q 3 K Q 2 Q 1 Increasing Output

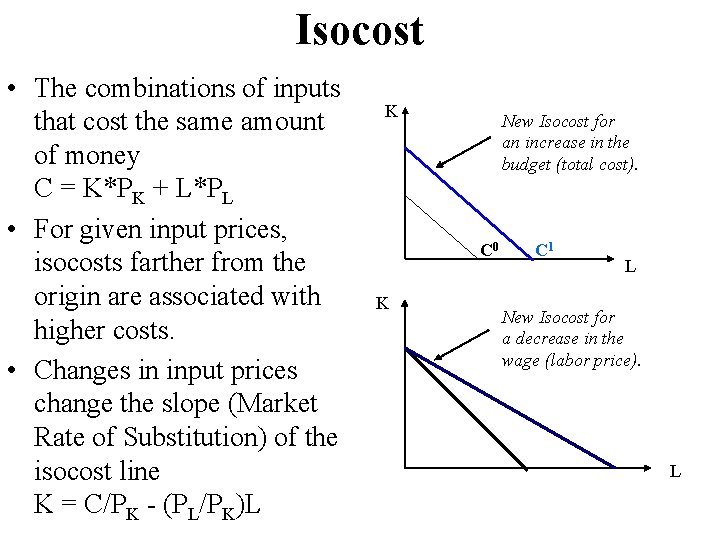
Isocost • The combinations of inputs that cost the same amount of money C = K*PK + L*PL • For given input prices, isocosts farther from the origin are associated with higher costs. • Changes in input prices change the slope (Market Rate of Substitution) of the isocost line K = C/PK - (PL/PK)L K New Isocost for an increase in the budget (total cost). C 0 K C 1 L New Isocost for a decrease in the wage (labor price). L

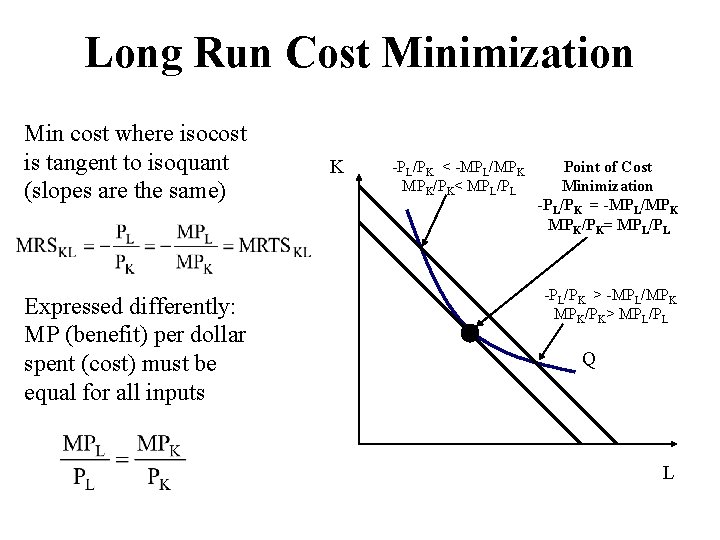
Long Run Cost Minimization Min cost where isocost is tangent to isoquant (slopes are the same) Expressed differently: MP (benefit) per dollar spent (cost) must be equal for all inputs K -PL/PK < -MPL/MPK MPK/PK< MPL/PL Point of Cost Minimization -PL/PK = -MPL/MPK MPK/PK= MPL/PL -PL/PK > -MPL/MPK MPK/PK> MPL/PL Q L

Returns to Scale • Return (MP): How TP changes when one input increases • RTS: How TP changes when all inputs increase by the same multiple λ > 0 • Q = f(K, L) • • Q = 50 K½L½ Q = 100, 000 + 500 L + 100 K Q = 0. 01 K 3 + 4 K 2 L + L 2 K + 0. 0001 L 3

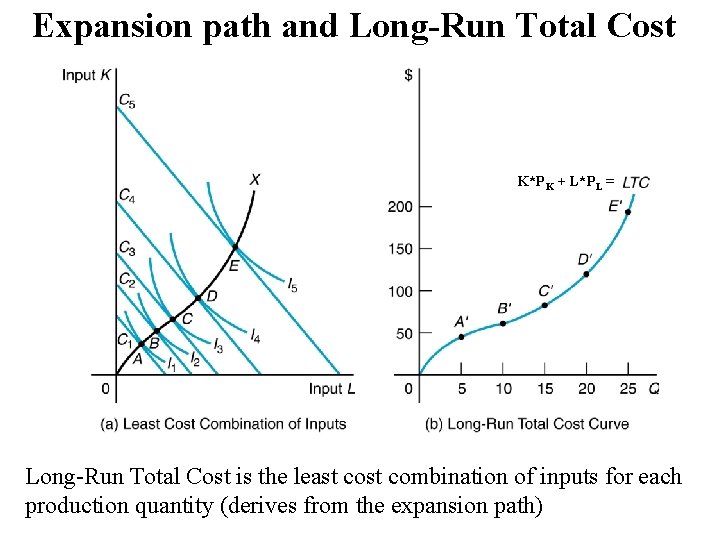
Expansion path and Long-Run Total Cost K*PK + L*PL = Long-Run Total Cost is the least combination of inputs for each production quantity (derives from the expansion path)

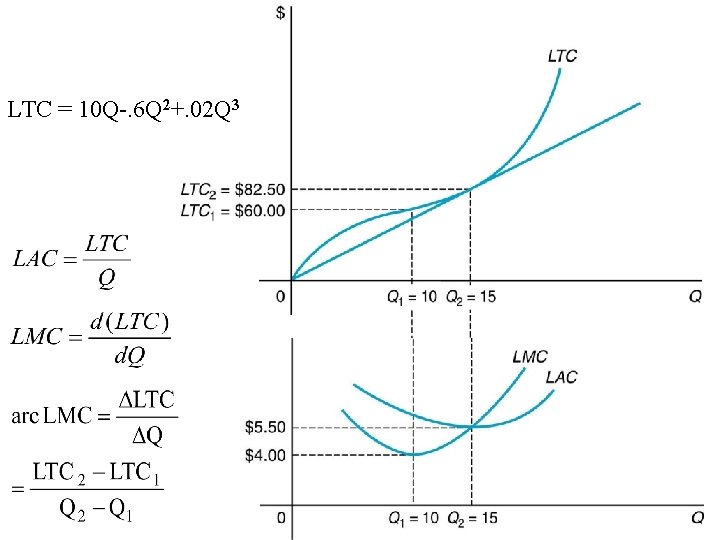
LTC = 10 Q-. 6 Q 2+. 02 Q 3

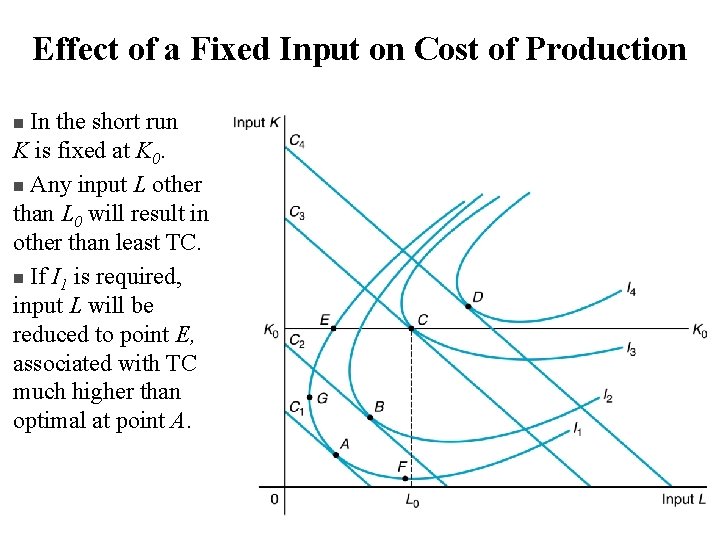
Effect of a Fixed Input on Cost of Production In the short run K is fixed at K 0. n Any input L other than L 0 will result in other than least TC. n If I 1 is required, input L will be reduced to point E, associated with TC much higher than optimal at point A. n

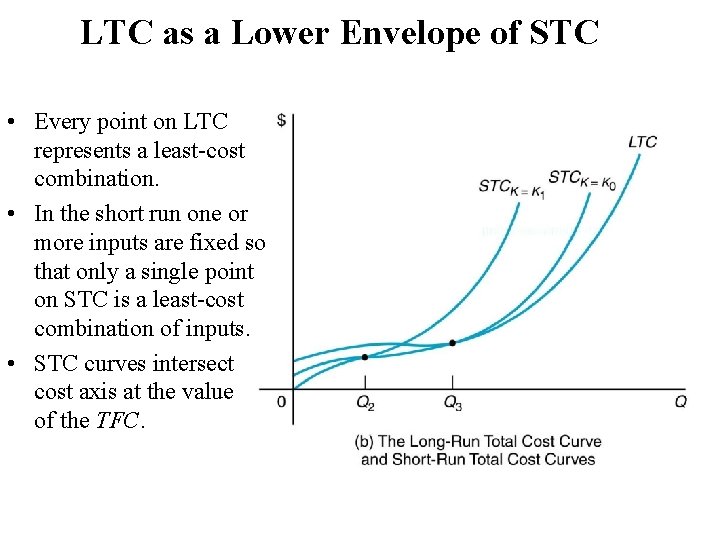
LTC as a Lower Envelope of STC • Every point on LTC represents a least-cost combination. • In the short run one or more inputs are fixed so that only a single point on STC is a least-cost combination of inputs. • STC curves intersect cost axis at the value of the TFC.

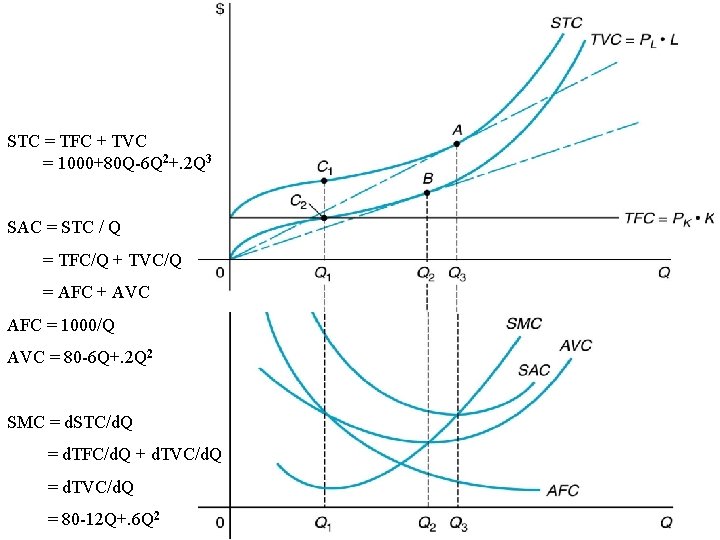
STC = TFC + TVC = 1000+80 Q-6 Q 2+. 2 Q 3 SAC = STC / Q = TFC/Q + TVC/Q = AFC + AVC AFC = 1000/Q AVC = 80 -6 Q+. 2 Q 2 SMC = d. STC/d. Q = d. TFC/d. Q + d. TVC/d. Q = 80 -12 Q+. 6 Q 2

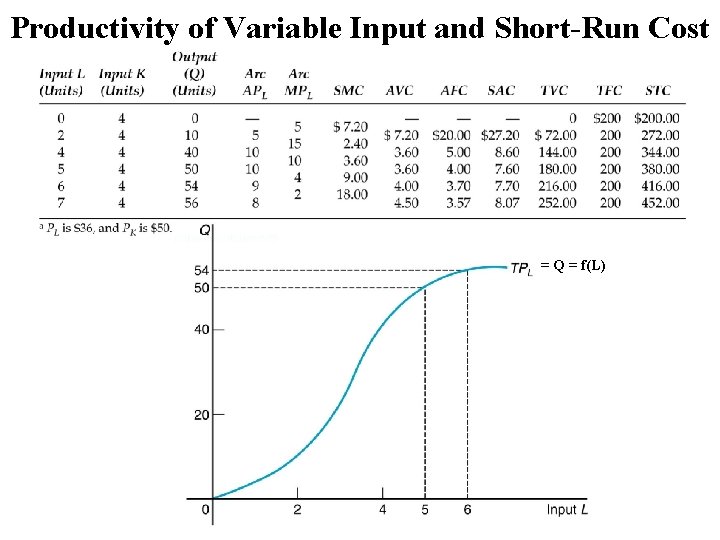
Productivity of Variable Input and Short-Run Cost = Q = f(L)

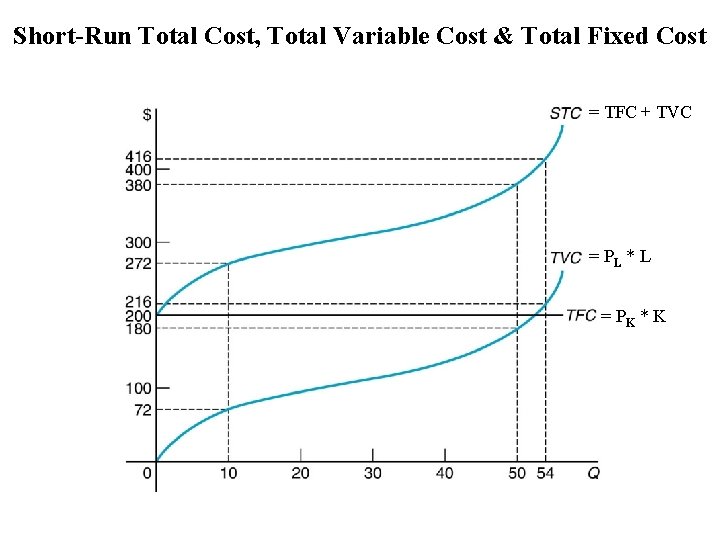
Short-Run Total Cost, Total Variable Cost & Total Fixed Cost = TFC + TVC = PL * L = PK * K

Average Product and Average Variable Cost

Marginal Product and Short-Run Marginal Cost

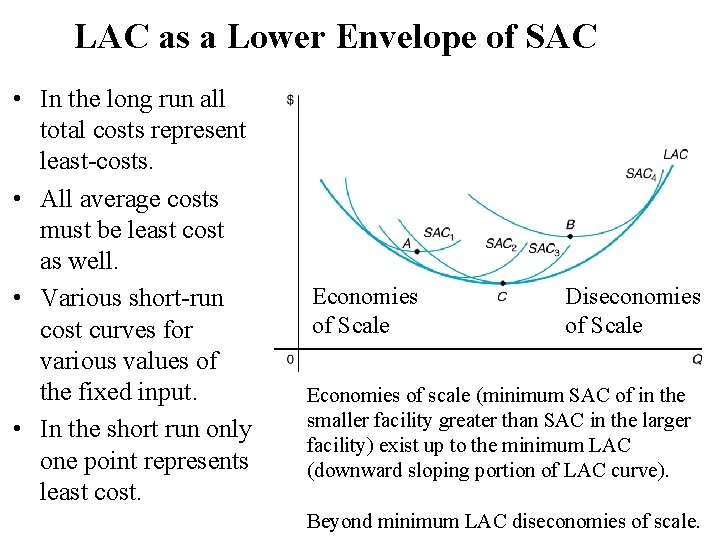
LAC as a Lower Envelope of SAC • In the long run all total costs represent least-costs. • All average costs must be least cost as well. • Various short-run cost curves for various values of the fixed input. • In the short run only one point represents least cost. Economies of Scale Diseconomies of Scale Economies of scale (minimum SAC of in the smaller facility greater than SAC in the larger facility) exist up to the minimum LAC (downward sloping portion of LAC curve). Beyond minimum LAC diseconomies of scale.

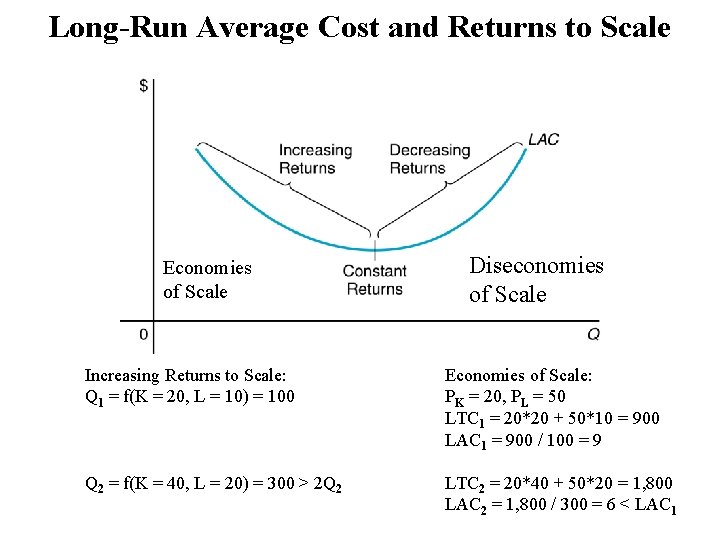
Long-Run Average Cost and Returns to Scale Economies of Scale Diseconomies of Scale Increasing Returns to Scale: Q 1 = f(K = 20, L = 10) = 100 Economies of Scale: PK = 20, PL = 50 LTC 1 = 20*20 + 50*10 = 900 LAC 1 = 900 / 100 = 9 Q 2 = f(K = 40, L = 20) = 300 > 2 Q 2 LTC 2 = 20*40 + 50*20 = 1, 800 LAC 2 = 1, 800 / 300 = 6 < LAC 1

Economies of Scope and Cost Complementarity • Cheaper to produce outputs jointly than separately: C(Q 1, Q 2) < C(Q 1, 0) + C(0, Q 2) • MC of producing good 1 declines as more of good 2 is produced: MC 1 / Q 2 < 0 • Example: Joint processing of deposit accounts and loans in banks Scope: Single financial advisor eliminates duplicate common factors of production (computers, loan production offices) Complementarity: Account and credit information developed for deposits lowers credit check and monitoring cost for loans. Expansion of deposit base lowers cost of providing loans.

Quadratic Multi-Product Cost Function • C(Q 1, Q 2) = f + a. Q 1 Q 2 + (Q 1 )2 + (Q 2 )2 MCi(Qi, Qj) = a. Qj + 2 Qi • Economies of scope (cheaper joint product) if : f > a. Q 1 Q 2 C(Q 1, 0) + C(0, Q 2 ) = f + (Q 1)2 + f + (Q 2)2 • Cost complementarity exists if: a < 0 MCi/ Qj = a < 0

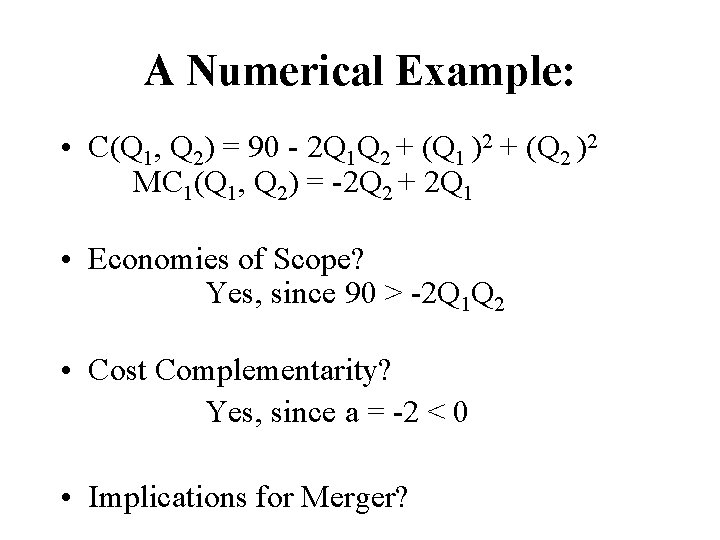
A Numerical Example: • C(Q 1, Q 2) = 90 - 2 Q 1 Q 2 + (Q 1 )2 + (Q 2 )2 MC 1(Q 1, Q 2) = -2 Q 2 + 2 Q 1 • Economies of Scope? Yes, since 90 > -2 Q 1 Q 2 • Cost Complementarity? Yes, since a = -2 < 0 • Implications for Merger?