The Problem with Integer Programming H P Williams

The Problem with Integer Programming H. P. Williams London School of Economics

The Nature of Integer Programming (IP) Ø Is IP like Linear Programming (LP) ? Ø Applications of Integer Programming Ø Mathematical Properties of IP Ø Economic Properties of IP Ø Chvátal Functions and Integer Monoids

A General (Mixed) Integer Programme (IP) Maximise/Minimise ∑j cjxj+∑kdkyk Subject to : ∑jaijxj +∑keikyk <=> bi for all i xj>=0 all j, yk>=0 all k and integer

A General (Mixed) Integer Programme Ø Frequently (but not always) the integer variables are restricted to values 0 and 1 representing (indivisible) Yes/No decisions eg. Investment Ø Can view as a Logical statement about a series of Linear Programmes (LPs) Ø Leads a to close relationship between Logic and IP

0 -1 Integer Programmes Ø Any IP with bounded integer variables can be converted to a 0 -1 IP Ø 0 -1 IPs can be interpreted as Disjunctions of LPs Ø Application of logical methods to formulation and solution

Applications of IP Ø Extensions to LPs eg Manufacturing, Distribution, Petroleum, Gas and Chemicals Ø Ø Ø Ø Global Optimisation of non-convex (non-linear) models Power Systems Loading Facilities Location Routing Telecommunications Medical Radiation Statistical Design Molecular Biology Genome Sequencing Archaeological Seriation Optimal Logical Statements Computer Design Aircraft Scheduling Crew Rostering

Linear Programming v Integer Programming An LP Minimise X 2 Subject to: 2 X 1+X 2 >=13 5 X 1+2 X 2<=30 -X 1+X 2 >=5 X 1 , X 2 >= 0 Ø The Solution Ø X 1 = 22/3 , X 2 = 72/3

Linear Programming v Integer Programming An LP Minimise X 2 Subject to: 2 X 1+X 2 >=13 5 X 1+2 X 2<=30 -X 1+X 2 >=5 X 1 , X 2 >= 0 Ø An IP Minimise X 2 Subject to: 2 X 1 + X 2 >=13 5 X 1 + 2 X 2<=30 -X 1 + X 2 >=5 X 1 , X 2 >= 0 and integer Ø The Solution Ø X 1 = 22/3 , X 2 = 72/3

Linear Programming v Integer Programming An LP Minimise X 2 Subject to: 2 X 1+X 2 >=13 5 X 1+2 X 2<=30 -X 1+X 2 >=5 X 1 , X 2 >= 0 Ø An IP Minimise X 2 Subject to: 2 X 1 + X 2 >=13 5 X 1 + 2 X 2<=30 -X 1 + X 2 >=5 X 1 , X 2 >= 0 and integer The Solution Ø X 1 = 22/3 , X 2 = 72/3 Ø The Solution Ø X 1 = 2 , X 2 = 9

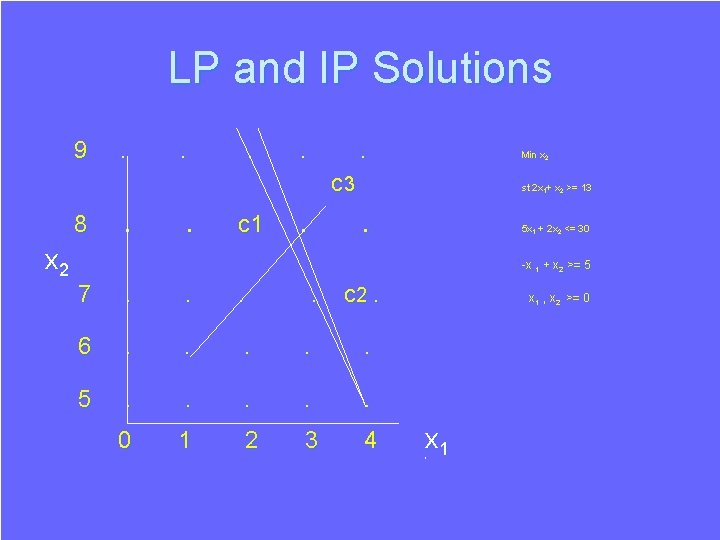
LP and IP Solutions 9 . . . Min x 2 c 3 8 x 2 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

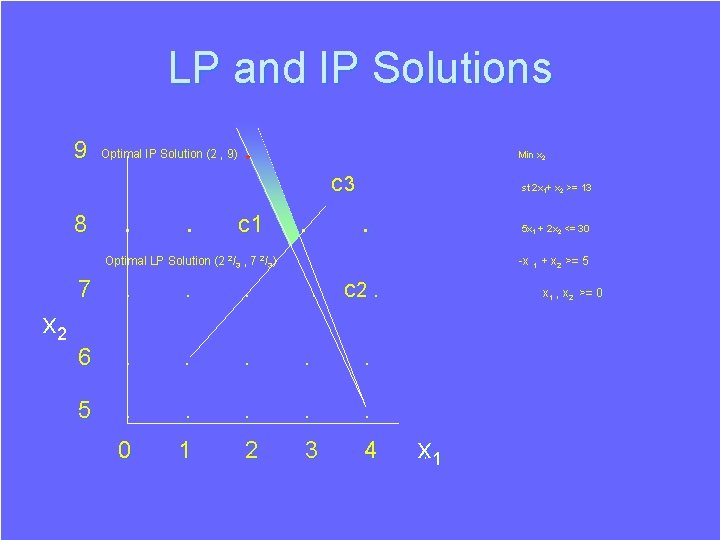
LP and IP Solutions 9 Optimal IP Solution (2 , 9) . • Min x 2 c 3 8 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 Optimal LP Solution (2 2/3 , 7 2/3) x 2 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

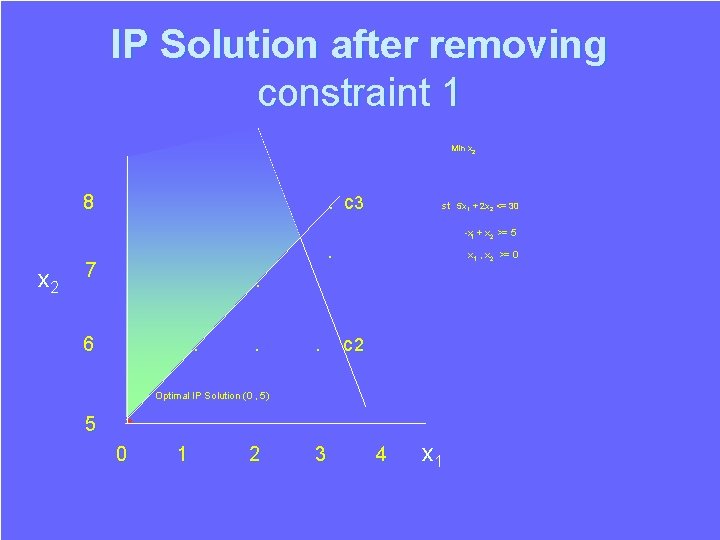
IP Solution after removing constraint 1 Min x 2 8 x 2 . . 7 6 . c 1 . . . . c 3 . . . st 5 x 1 + 2 x 2 <= 30 -x 1 + x 2 >= 5 . . x 1 , x 2 >= 0 c 2 Optimal IP Solution (0 , 5) 5 • 0 1 2 3 4 x 1

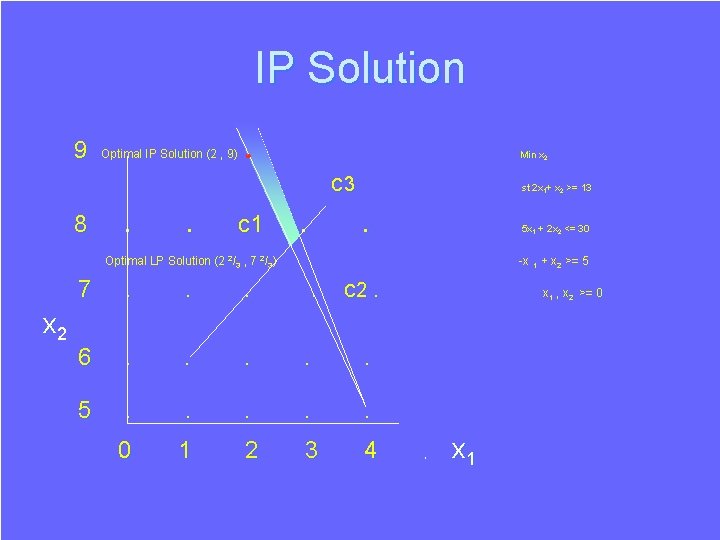
IP Solution 9 Optimal IP Solution (2 , 9) . • Min x 2 c 3 8 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 Optimal LP Solution (2 2/3 , 7 2/3) x 2 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

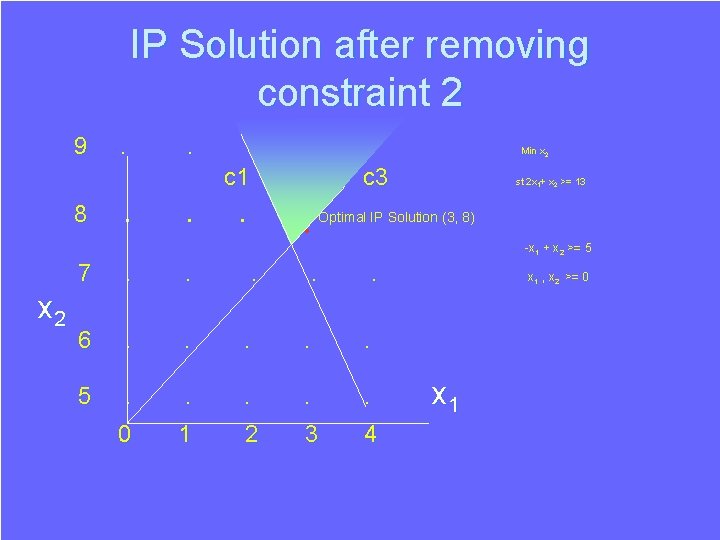
IP Solution after removing constraint 2 9 8 . . . c 1 . Min x 2 c 3 st 2 x 1+ x 2 >= 13 . • Optimal IP Solution (3, 8) -x 1 + x 2 >= 5 x 2 7 . . . 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

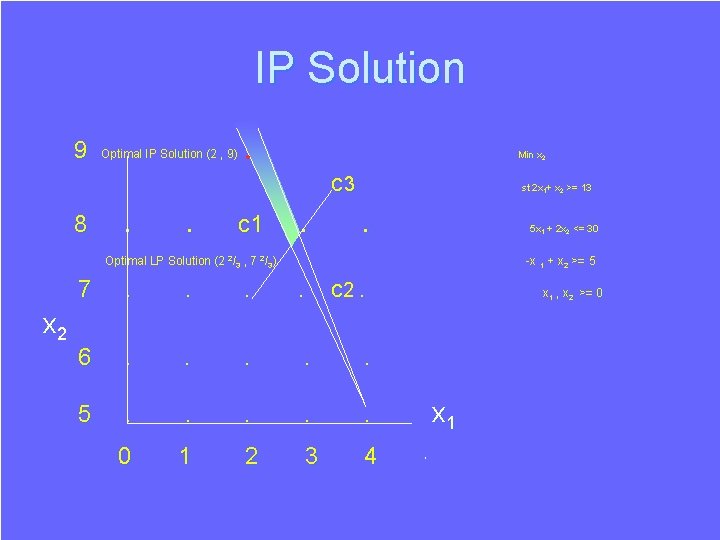
IP Solution 9 Optimal IP Solution (2 , 9) . • Min x 2 c 3 8 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 Optimal LP Solution (2 2/3 , 7 2/3) x 2 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

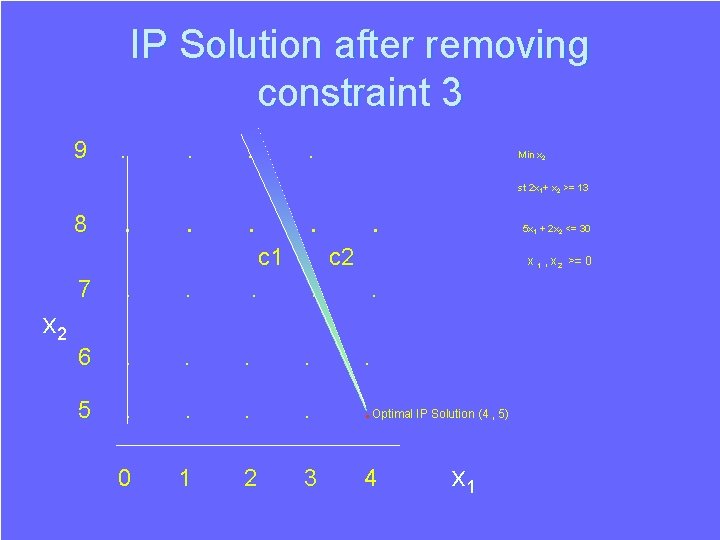
IP Solution after removing constraint 3 9 . . Min x 2 st 2 x 1+ x 2 >= 13 8 x 2 . . . . 5 x 1 + 2 x 2 <= 30 7 . . c 1. c 2 6 . . . 5 . . . Optimal IP Solution (4 , 5) 0 1 2 3 4 x 1 , x 2 >= 0 x 1

Rounding often not satisfactory Example: The Alabama Paradox Ø State Population Fair solution Rounded Solution With 10 Representatives A 621 k 4. 41 4 B 587 k 4. 17 4 C 201 k 1. 43 2 A B C With 11 Representatives 621 k 4. 85 5 587 k 4. 58 5 201 k 1. 57 1

IP Formulation of Political Apportionment Problem Vi = Population (Votes cast) for State (Party) i xi = Seats allotted to State (Party) i Choose xi so as to: Min Maxi (xi / vi) st ∑ixi = Total Number of Seats x i >= 0 and integer for all I ie Min y st xi / vi <= y for all i ∑ i xi = Total Number of Seats xi >= 0 and integer for all I LP Relaxation gives fractional solution IP Solution give Jefferson/D’Hondt solution

IP Solution Ø State Population A B C Fractional solution (LP) Rounded solution Jefferson/ D’Hondt solution (IP) 621 k 587 k 201 k With 10 Representatives 4. 41 4 4. 17 4 1. 43 2 5 4 1 621 k 587 k 201 k With 11 Representatives 4. 85 5 4. 58 5 1. 57 1 5 5 1

Mathematical Differences between LP and IP Ø Consider a (Pure) IP in standard form Maximise c 1 x 1 + c 2 x 2 + … + cnxn Subject to: a 11 x 1 + a 12 x 2 + … a 1 nxn <= b 1 a 21 x 1 + a 22 x 2 + … a 2 nxn <= b 2. . am 1 x 1+ am 2 x 2 + … amnxn <= bm x 1 , x 2 , … , xn >= 0 and integer

Mathematical Differences between LP and IP Ø LP IP If has Optimal Solution there is one with at most m variables positive (a basic solution) No limit on number of positive variables At most n constraints binding at optimum At most 2 n – 1 constraints binding at optimum There are valuations on constraints which close duality gap ie there is a (symmetric) LP (dual) model Chvátal Functions Hilbert Basis (no fixed dimension) No obvious symmetry

IPs involve Lattices within Polytopes Eg Max 2 x 1+x 2 st 2 x 1+9 x 2<=80 2 x 1 -3 x 2<=6 -x 1 <=0 -x 2<=0 2 x 1+3 x 2 ≡ 0(mod 12) x 1 ≡ 0(mod 1) x 2≡ 0(mod 1)

What are the strongest implications? Max 2 x 1+x 2 st 2 x 1+9 x 2<=80 2 x 1 -3 x 2<=6 -x 1 <=0 -x 2<=0 2 x 1+3 x 2 ≡ 0(mod 12) x 1 ≡ 0(mod 1) x 2≡ 0(mod 1) 2 x 1+9 x 2<=80 2 x 1 -3 x 2<=6 -x 1 <=0 -x 2<=0 2 x 1+3 x 2 ≡ 0(mod 12) x 1 ≡ 0(mod 1) x 2 ≡ 0(mod 1) 2 x 1+x 2 ?

What are the strongest implications? Dual arguments. Max 2 x 1+x 2 st 2 x 1+9 x 2<=80 2 x 1 -3 x 2<=6 -x 1 <=0 -x 2<=0 2 x 1+3 x 2 ≡ 0(mod 12) x 1 ≡ 0(mod 1) x 2≡ 0(mod 1) 2 x 1+9 x 2<=80 2 x 1 -3 x 2<=6 -x 1 <=0 -x 2<=0 ⅓ ⅔ 0 0 2 x 1+3 x 2 ≡ 0(mod 12) 3 x 1 ≡ 0(mod 1) 0 x 2 ≡ 0(mod 1) 4 2 x 1+x 2 <= 302/3 2 x 1+x 2 Ξ 0(mod 4)

IPs involve Lattices within Polytopes 8 . . . 4 . . Objective = 302/3 . Objective = 28 . . 0 6 . Objective = 24 12

IPs involve Lattices within Polytopes Optimisation over polytopes give strongest (LP) bound on objective Optimisation over lattices give strongest congruence relation for objective Combined they give rank 1 cut for objective This may not be adequate

Lattices within Cones give Integer Monoids These are a fundamental structure for IP

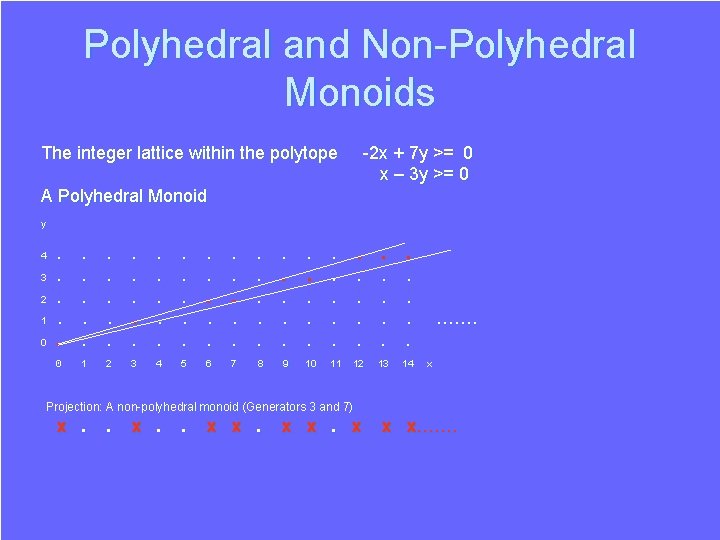
Polyhedral and Non-Polyhedral Monoids The integer lattice within the polytope -2 x + 7 y >= 0 x – 3 y >= 0 A Polyhedral Monoid y 4 3 2 1 0 . . . . . 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 ……. x Projection: A non-polyhedral monoid (Generators 3 and 7) x. . x x x…….

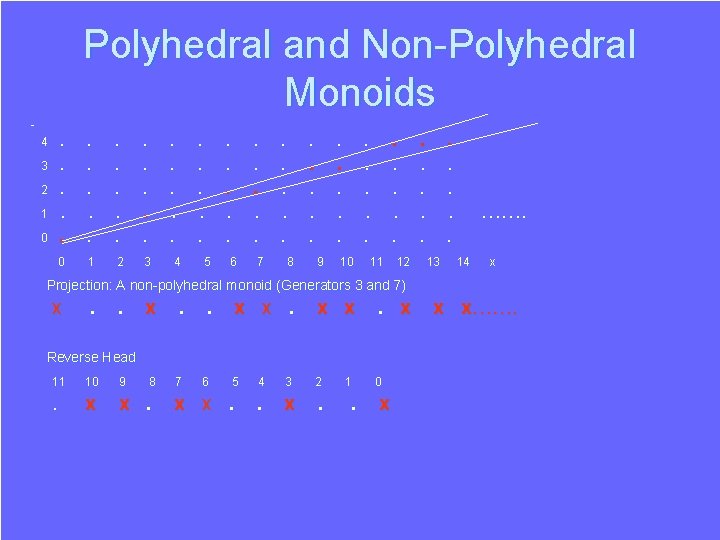
Polyhedral and Non-Polyhedral Monoids. . . . . 0 1 2 3 4 3 2 1 0 . . . 4 5 6 7 8 9 10 11 12 13 ……. 14 x Projection: A non-polyhedral monoid (Generators 3 and 7) x . 8 7 . x x . x 5 0 Reverse Head 11 10 9 . x x. 6 x x. 4 3 2 . x . 1 . x x x…….

Duality in LP and IP The Value Function of an LP Minimise x 2 subject to: 2 x 1 + x 2 >= b 1 5 x 1 + 2 x 2 <= b 2 -x 1 + x 2 >= b 3 x 1 , x 2 >= 0 Value Function of LP is Max( 5 b 1 - 2 b 2 , 1/3( b 1 + 2 b 3) , b 3) If b 1 = 13, b 2 = 30, b 3 = 5 we have Max( 5, 72/3 , 5 ) = 72/3 , Consistency Tester is Max( 2 b 1 – b 2 , -b 2 + 2 b 3 ) <= 0 giving Max( -4, -30, -20) <= 0. (5, -2, 0), (1/3, 0, 2/3), (0, 0, 1) are vertices of Dual Polytope. They give marginal rates of change (shadow prices) of optimal objective with respect to b 1, b 2, b 3. (5, -2, , 0), (1/3, 0, 2/3), (0, 0, 1) are extreme rays of Dual Polytope. What are the corresponding quantities for an IP ?

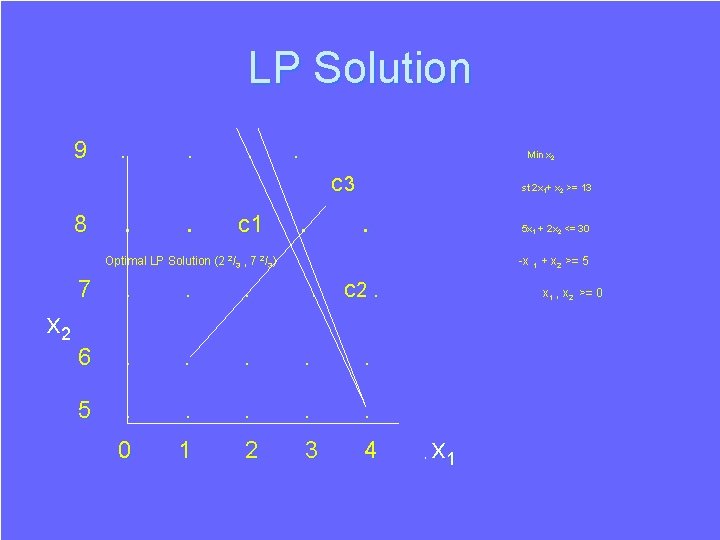
LP Solution 9 . . Min x 2 c 3 8 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 Optimal LP Solution (2 2/3 , 7 2/3) x 2 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

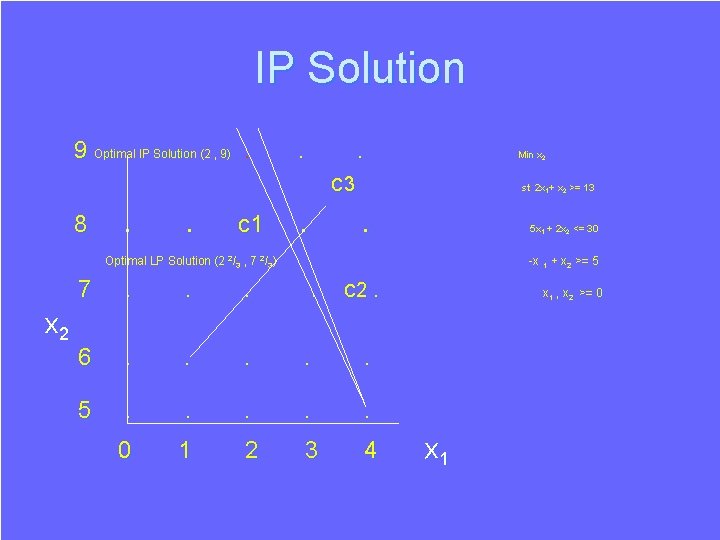
IP Solution 9 Optimal IP Solution (2 , 9). . . Min x 2 c 3 8 . . c 1 . st 2 x 1+ x 2 >= 13 . 5 x 1 + 2 x 2 <= 30 Optimal LP Solution (2 2/3 , 7 2/3) x 2 -x 1 + x 2 >= 5 7 . . c 2. 6 . . . 5 . . . 0 1 2 3 4 x 1 , x 2 >= 0 x 1

Duality in LP and IP The Value Function of an IP Minimise x 2 subject to: 2 x 1 + x 2 >= b 1 5 x 1 + 2 x 2 <= b 2 -x 1 + x 2 >= b 3 x 1 , x 2 >= 0 and integer Value Function of IP is Max( 5 b 1 - 2 b 2 , ┌1/3( b 1 + 2 b 3) ┐ , b 3 , b 1+ 2 ┌ 1/5 (-b 2+ 2 ┌ 1/3(b 1 + 2 b 3) ┐ ) This is known as a Gomory Function. The component expressions are known as Chvάtal Functions.

Gomory and Chvátal Functions ┌ ┐ ┌ ┌ ┐ ┐ Max( 5 b 1 -2 b 2, ┌1/3(b 1 + 2 b 3) ┐, b 3 , b 1+ 2 ┌1/5 (-b 2+ 2 ┌1/3(b 1 + 2 b 3) ┐ ) If b 1=13, b 2=30, b 3=5 we have Max(5, 8, 5, 9)=9 Chvátal Function the optimum. ┌ ┌ ┐ ┐ determines b 1+ 2 1/5 (-b 2+ 2 1/3(b 1 + 2 b 3) ) LP Relaxation is 19/15 b 1 - 2/5 b 2 +8/15 b 2 (19/15, -2/5, 8/15) is an interior point of dual polytope but (5, -2, 0) and (1/3, 0, 2/3) are vertices of dual corresponding to possible LP optima (for different bi )

Why are valuations on discrete resources of interest ? Allocation of Fixed Costs Maximise ∑j pi xi - f y st xi - Di y <= 0 for all I y ε {0, 1} depending on whether facility built. f is fixed cost. xi is level of service provided to i (up to level Di ) pi is unit profit to i. A ‘dual value’ vi on xi - Di y <= 0 would result in Maximise ∑j (pi – vi ) xi - (f – (∑j D i v i) y Ie an allocation of the fixed cost back to the ‘consumers’

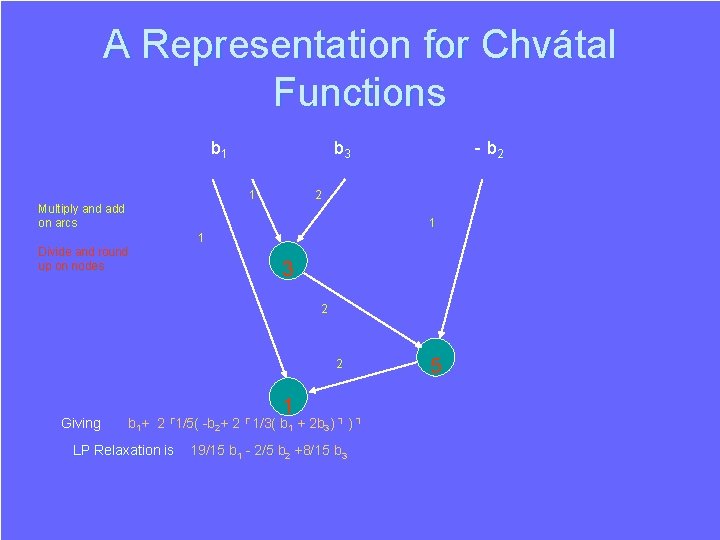
A Representation for Chvátal Functions b 1 b 3 1 - b 2 2 Multiply and add on arcs 1 1 Divide and round up on nodes 3 2 2 Giving 1 b 1+ 2 ┌1/5( -b 2+ 2 ┌ 1/3( b 1 + 2 b 3) ┐ LP Relaxation is 19/15 b 1 - 2/5 b 2 +8/15 b 3 5

Simplifications sometimes possible ┌2 ┌ 7 ┐ ┐ /7 /3 n Ø Ø But ┌ 2 ┐ ┐ /3 /7 n ┌ 1 ┌5 /3 /6 Ø Ø ┌7 But ┌ 2 ┌5 /3 /6 n ┐ ┐ ≡ ┌ 2 ┐ /3 n ≠ ┌ 2 ┐ /3 n ≡ ≠ Is there a Normal Form ? eg n = 1 ┌ 5 ┐ /18 n ┌ 5 ┐ /9 n eg n=5

Properties of Chvátal Functions Ø They involve non-negative linear combinations (with possibly negative coefficients on the arguments) and nested integer round-up. Ø They obey the triangle inequality. Ø They are shift-periodic ie value is increased in cyclic pattern with increases in value of arguments. Ø They take the place of inequalities to define non-polyhedral integer monoids.

The Triangle Inequality Ø Ø ┐ ┌ ┐ a + b ┌ >= ┐ a + b ┌ Hence of value in defining Discrete Metrics

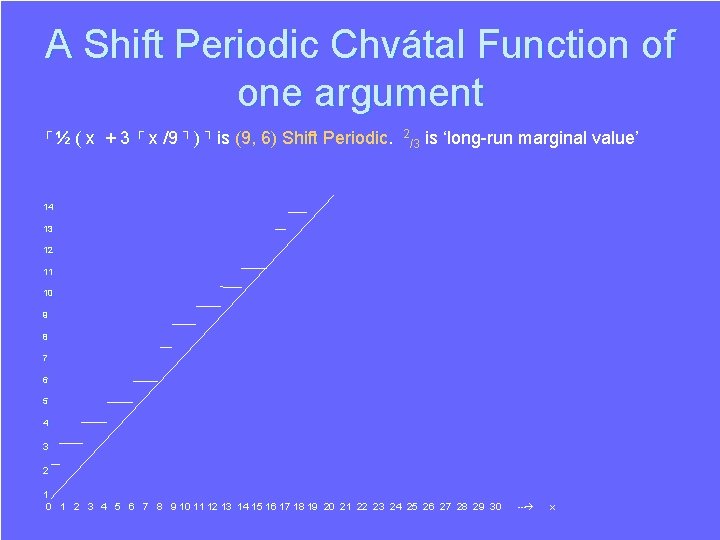
A Shift Periodic Chvátal Function of one argument ┌ ┌ ┐ ┐ ½ ( x + 3 ┌ x /9 ┐ ) ┐ is (9, 6) Shift Periodic. 2 /3 is ‘long-run marginal value’ 14 13 12 11 10 9 8 7 6 5 4 3 2 1. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 --- x

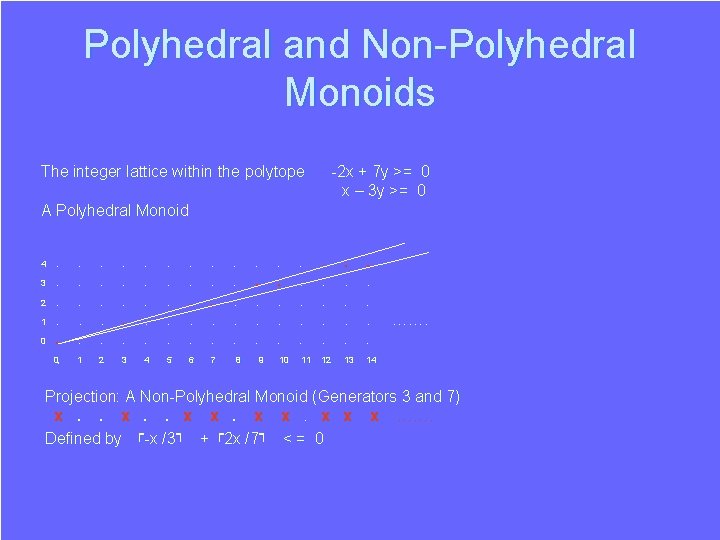
Polyhedral and Non-Polyhedral Monoids The integer lattice within the polytope -2 x + 7 y >= 0 x – 3 y >= 0 A Polyhedral Monoid 4 3 2 1 0 . . 0 1 2 3 4 5 6 7 . . . 8 . . . 9 . . . 10 . . . 11 . . . . 12 13 14 ……. Projection: A Non-Polyhedral Monoid (Generators 3 and 7) x. . x x x ……. Defined by ┌-x /3┐ + ┌2 x /7┐ < = 0

Finally Ø We should be Optimising Chvátal Functions over Integer Monoids

References Ø CE Blair and RG Jeroslow, The value function of an integer programme, Mathematical Programming 23(1982) 237 -273. Ø V Chvátal, Edmonds polytopes and a hierarchy of combinatorial problems, Discrete Mathematics 4(1973) 305 -307. Ø D. Kirby and HP Williams, Representing integral monoids by inequalities Journal of Combinatorial Mathematics and Combinatorial Computing 23 (1997) 87 -95. Ø F Rhodes and HP Williams Discrete subadditive functions as Gomory functions, Mathematical Proceedings of the Cambridge Philosophical Society 117 (1995) 559 -574. Ø HP Williams, A Duality Theorem for Linear Congruences, Discrete Applied Mathematics 7 (1984) 93 -103. Ø HP Williams, Constructing the value function for an integer linear programme over a cone, Computational Optimisation and Applications 6 (1996) 15 -26. Ø LA Wolsey, The b-hull of an integer programme, Discrete Applied Mathematics 3(1981) 193201.