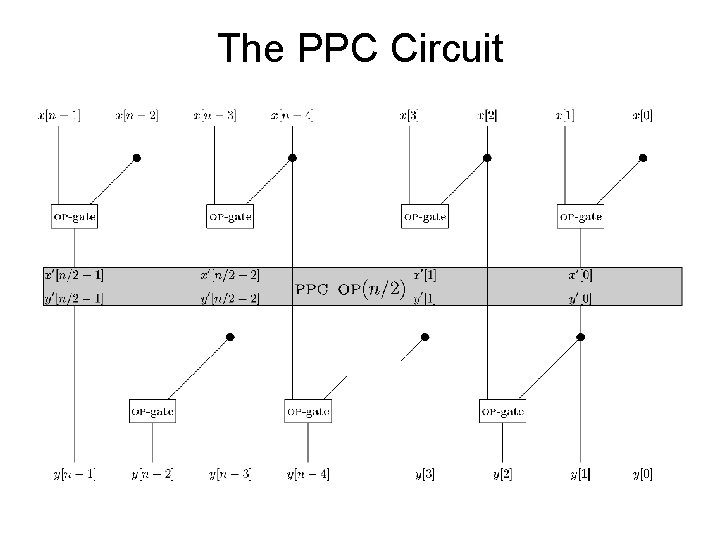
The PPC Circuit Fanout of a PPC Circuit







![PPC for Decimal Addition • Reduction to carry bit computation: S[i] = mod( A[i]+B[i]+C[i] PPC for Decimal Addition • Reduction to carry bit computation: S[i] = mod( A[i]+B[i]+C[i]](https://slidetodoc.com/presentation_image_h/1b5dde892ada1ae3823260ec28513e48/image-10.jpg)
![Defining the Alphabet For i=-1: 2·C[0] = 0 or 2 σ[i] = For i≥ Defining the Alphabet For i=-1: 2·C[0] = 0 or 2 σ[i] = For i≥](https://slidetodoc.com/presentation_image_h/1b5dde892ada1ae3823260ec28513e48/image-11.jpg)




- Slides: 15


The PPC Circuit

Fan-out of a PPC Circuit Upper Bound: • There is a constant maximum number of splits per layer. • There are O(log n) layers. • Therefore, the total number of splits is O(log n).

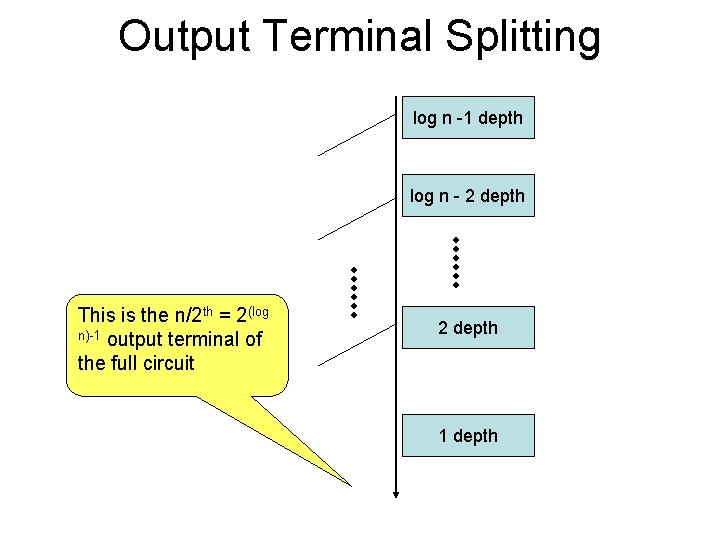
Fan-out of a PPC circuit (2) Lower Bound: • For simplicity, let us renumber the terminals beginning with 1 instead of 0. • Observe that the even numbered outputs are split once just before the exit. • Also observe that even numbered outputs of each circuit come from an internal circuit.

Fan-out of a PPC circuit (3) • Let us look at the n/2 = 2(log n)-1 output terminal. • It will be an Even numbered output terminal of log(n)– 2 circuits in the recursive construction.

Output Terminal Splitting log n -1 depth log n - 2 depth This is the n/2 th = 2(log n)-1 output terminal of the full circuit 2 depth 1 depth

Fan-out of a PPC circuit (4) • Thus, the right most terminal will split log(n)-2 times and have a fan-out of log n - 1. • Since we have shown an example that achieves the Upper Bound, the Lower Bound must be equal to the Upper Bound.

Operator *

Operator *
![PPC for Decimal Addition Reduction to carry bit computation Si mod AiBiCi PPC for Decimal Addition • Reduction to carry bit computation: S[i] = mod( A[i]+B[i]+C[i]](https://slidetodoc.com/presentation_image_h/1b5dde892ada1ae3823260ec28513e48/image-10.jpg)
PPC for Decimal Addition • Reduction to carry bit computation: S[i] = mod( A[i]+B[i]+C[i] , 10 ) • This is a constant time reduction since the addition of 3 BCD coded decimal digits can be done in constant time. • The price is linear since it is a constant price per decimal digit. The problem is reduced to the calculation of the carry bits.
![Defining the Alphabet For i1 2C0 0 or 2 σi For i Defining the Alphabet For i=-1: 2·C[0] = 0 or 2 σ[i] = For i≥](https://slidetodoc.com/presentation_image_h/1b5dde892ada1ae3823260ec28513e48/image-11.jpg)
Defining the Alphabet For i=-1: 2·C[0] = 0 or 2 σ[i] = For i≥ 0: 0 if A[i]+B[i] < 9 (kill carry) 1 if A[i]+B[i] = 9 (propagate carry) 2 if A[i]+B[i] > 9 (generate carry)

The Operator • The original * operator is what we need. • The meaning of the alphabet is the same as the one used in class: – 0 = kill carry – 1 = propagate the carry – 2 = generate a carry • Go through the lecture notes and convince yourselves that it works.

The Circuit • The carry bits are calculated using the PPC circuit. • We then use a BCD adder for each of the output digits: S[i]=mod(A[i], B[i], C[i], 10)

2’s Complement Overflow

2’s Complement Overflow