The power point presentation is powered by AVTE

The power point presentation is powered by AVTE (Leader in CBSE Coaching) Issued in the Students Academic Interest 1

Greatest integer function returns the greatest integer less than or equal to a real number. In other words, greatest integer function rounds “down” any number to the nearest integer. This function is also known by the names of “floor” or “step” function. 2

Greatest integer function (Floor function) – Interpretation of Greatest integer function is straight forward for positive number. Consider the values “ 0. 23” and “ 1. 7”. The greatest integers for two numbers are “ 0” and “ 1”. – Now, consider a negative number “-0. 54” and “-2. 34”. The greatest integers less than these negative numbers are “-1” and “-3” respectively. 3
![Greatest Integer Function • The greatest integer function is denoted by the symbol “[x]”. Greatest Integer Function • The greatest integer function is denoted by the symbol “[x]”.](http://slidetodoc.com/presentation_image_h2/43542e348e014991c6eb5984a9a6bec5/image-4.jpg)
Greatest Integer Function • The greatest integer function is denoted by the symbol “[x]”. Working rules for evaluating greatest integer function are two step process : • If “x” is an integer, then [x] = x. • If “x” is not an integer, then [x] evaluates to greatest integer less than “x”. • In the nutshell, we can use any of the following interpretations of greatest integer function : • [x] = Greatest integer less than equal to “x” • [x] = Greatest integer not greater than “x” 4
![Greatest Integer Function • • • The value of "[x]" is an integer (n) Greatest Integer Function • • • The value of "[x]" is an integer (n)](http://slidetodoc.com/presentation_image_h2/43542e348e014991c6eb5984a9a6bec5/image-5.jpg)
Greatest Integer Function • • • The value of "[x]" is an integer (n) such that : f(x) =[x]=n; ifn≤x<n+1, n∈Z Graph of greatest integer function Few initial function values are : For − 2≤x<− 1, f(x) =[x]=− 2 For − 1≤x<0, f(x) =[x]=− 1 For 0≤x<1, f(x) =[x]=0 For 1 ≤x<2, f(x) =[x]=1 For 2≤x<3, f(x) =[x]=2 5
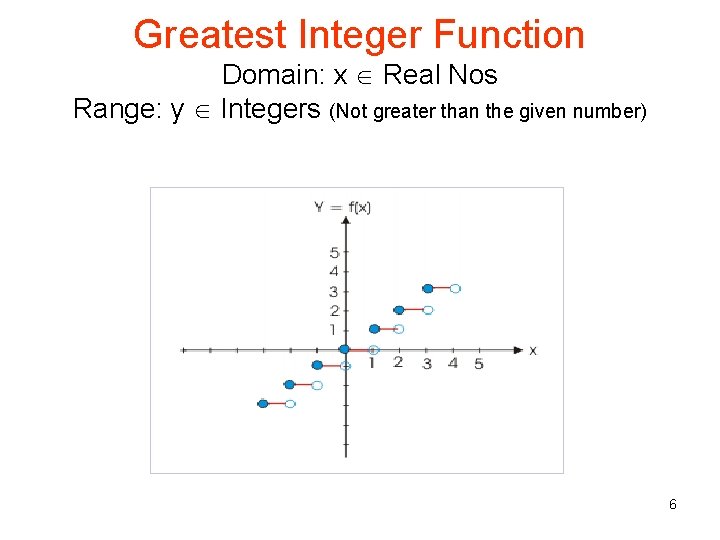
Greatest Integer Function Domain: x Real Nos Range: y Integers (Not greater than the given number) 6
- Slides: 6