The Power of Bar Modeling Applying Singapore Math

The Power of Bar Modeling: Applying Singapore Math Strategies at the Secondary Level Gregg Velatini Dianna Spence 2011 GCTM

Solving an Algebraic Equation n Six less than three times a number is fifteen. What is the number ? 21/3=7 7 21 6 15 The number is 7

Solving an Algebraic Equation--Practice n Three more than twice a number is eleven. What is the number ?

Solving an Algebraic Equation n Three more than twice a number is eleven. What is the number ? 2 x + 3 = 11 8 2 x = 8 4 1 1 1 x = 8/2 x=4 11 The number is 4

Solving an Algebraic Equation n The combined IQ’s of Mitt, Ron, and Barack is 397. Barack’s IQ is 7 points higher than Mitt’s, which is 15 points less than Ron’s. Find Barack’s IQ.

n The combined IQ’s of Mitt, Ron, and Barack is 397. Barack’s IQ is 7 points higher than Mitt’s, which is 15 points less than Ron’s. Find Barack’s IQ. Barack 7 397 Mitt Ron 15 Barack 7 397 - 15 = 375 Mitt Ron Barack 15 125 132 7 375 lbs / 3 = 125 Barack’s IQ is 125 + 7 = 132

Solving an Algebraic Equation -- Practice n The average weight of Peter, Paul and Mary is 80 lbs. Paul is twice as heavy as Mary. Peter is 10 lbs lighter than Paul. Find Paul’s weight.

Solving an Algebraic Equation n The average weight of Peter, Paul and Mary is 80 lbs. Paul is twice as heavy as Mary. Peter is 10 lbs lighter than Paul. Find Paul’s weight. Let M = Mary’s weight Paul W = Paul’s weight 80 x 3 = 240 lbs Mary P = Peter’s weight W = 2 M P = W – 10 Peter P+W+M = 240 10 lbs Re-Draw

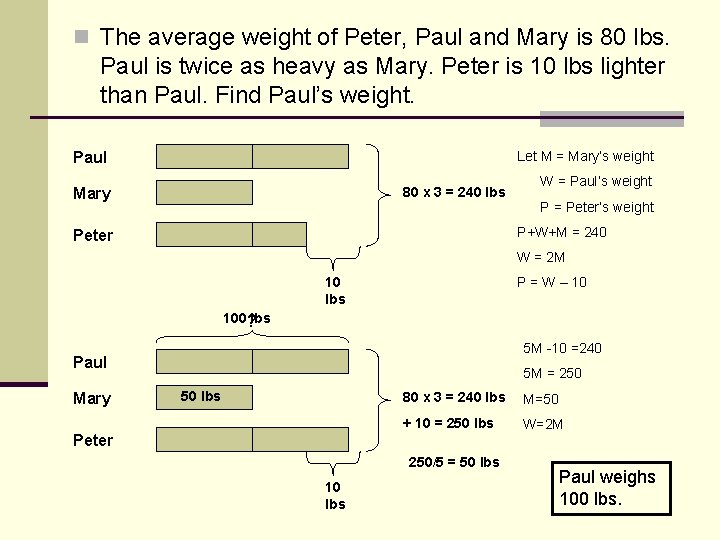
n The average weight of Peter, Paul and Mary is 80 lbs. Paul is twice as heavy as Mary. Peter is 10 lbs lighter than Paul. Find Paul’s weight. Let M = Mary’s weight Paul 80 x 3 = 240 lbs Mary W = Paul’s weight P = Peter’s weight P+W+M = 240 Peter W = 2 M 10 lbs P = W – 10 100 ? lbs 5 M -10 =240 Paul Mary 5 M = 250 50 lbs 80 x 3 = 240 lbs M=50 + 10 = 250 lbs W=2 M Peter 250/5 = 50 lbs 10 lbs Paul weighs 100 lbs.

Ratios and Proportions n A garbage man had 3 times as much money as a teacher. After the teacher earned an extra $200 moonlighting, the garbage man only had twice as much money. How much money did the teacher have at first? Garbage 3 Parts Teacher 1 Part

Ratios and Proportions n A garbage man had 3 times as much money as a teacher. After the teacher earned an extra $200 moonlighting, the garbage man only had twice as much money. How much money did the teacher have at first? Garbage 2 Parts 200 Teacher 1 Part The teacher had $400 at first.

Ratios and Proportions – Practice n The ratio of Clinton’s baseball cards to Jesse’s baseball cards was 3: 4. After Clinton bought another 40 baseball cards, he had twice as many baseball cards as Jesse. How many baseball cards did Clinton have at first?

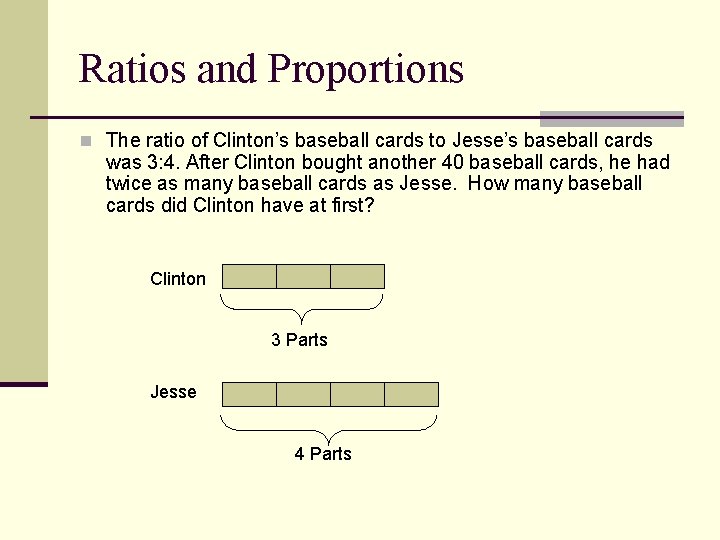
Ratios and Proportions n The ratio of Clinton’s baseball cards to Jesse’s baseball cards was 3: 4. After Clinton bought another 40 baseball cards, he had twice as many baseball cards as Jesse. How many baseball cards did Clinton have at first? Clinton 3 Parts Jesse 4 Parts

Ratios and Proportions n Set this up as a “Before and After” problem. Clinton 8 8 x 3 = 24 Before 3 Parts Clinton had 24 cards to begin with Jesse 4 Parts 40 Cards 8 Clinton 2 Parts Jesse 1 Part 40/5 = 8 After

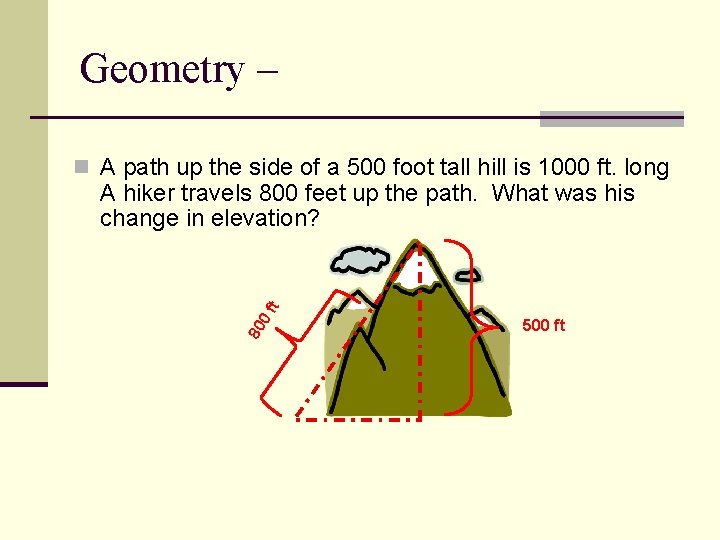
Geometry – n A path up the side of a 500 foot tall hill is 1000 ft. long 80 0 f t A hiker travels 800 feet up the path. What was his change in elevation? 500 ft

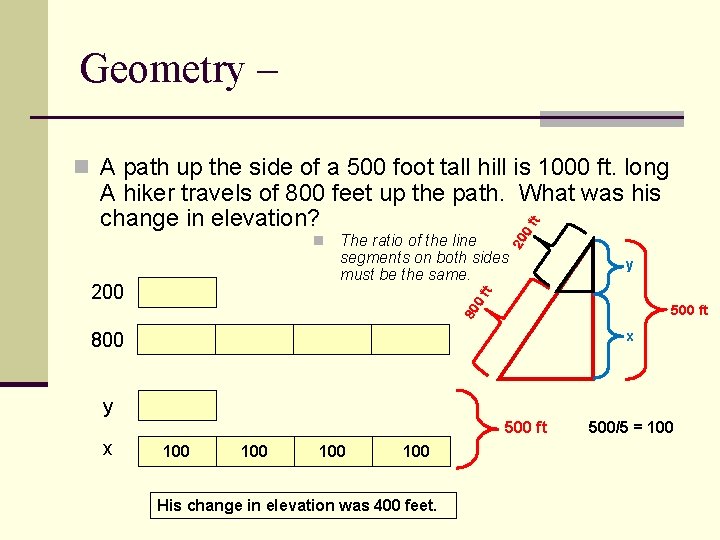
Geometry – n A path up the side of a 500 foot tall hill is 1000 ft. long y 0 f t 200 The ratio of the line segments on both sides must be the same. 20 n 0 f t A hiker travels of 800 feet up the path. What was his change in elevation? 80 500 ft x 800 y 500 ft x 100 100 His change in elevation was 400 feet. 500/5 = 100

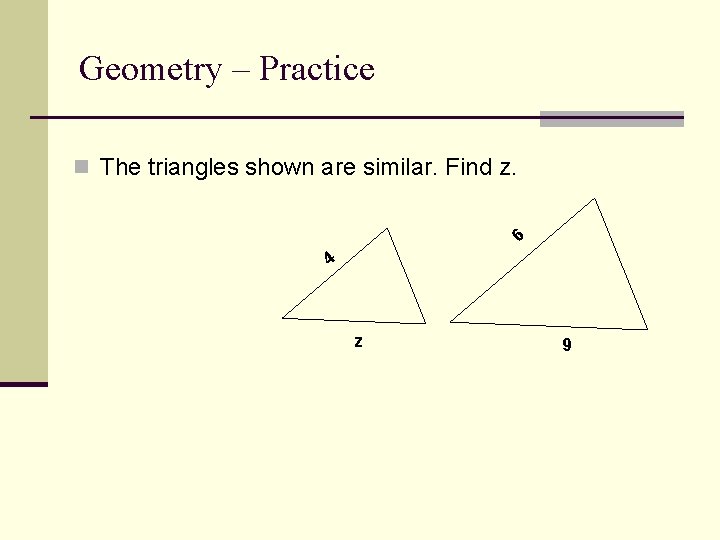
Geometry – Practice n The triangles shown are similar. Find z. 6 4 z 9

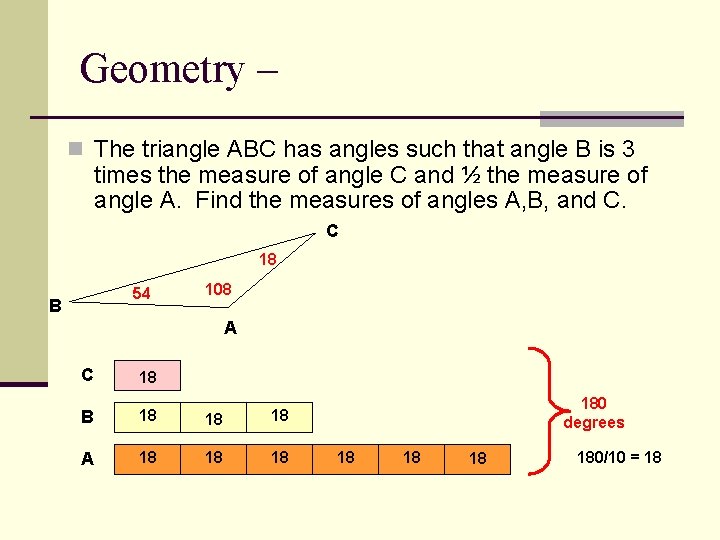
Geometry – n The triangle ABC has angles such that angle B is 3 times the measure of angle C and ½ the measure of angle A. Find the measures of angles A, B, and C. C 18 54 B 108 A C 18 B 18 18 18 A 18 180 degrees 18 180/10 = 18

Geometry – Practice n Angles A and B are complementary. Angle A is 2/3 the measure of angle B. Find the measure of angles A and B A B

Solving Fraction Equations n Sandy bought a box of cookies. 1/3 of the box was chocolate chip, 1/9 was oatmeal, 2/9 of the box were sugar cookies, and the rest were peanut butter. What fraction of the cookies were peanut butter? Box Chocolate Chip Oat Sugar Peanut Butter 3/9 n 1/3 of the cookies were peanut butter

Solving Fraction Equations-- Practice n Mom bought 1 carton of eggs. She used 1/6 of the eggs to make cookies an 1/4 of the eggs to bake a cake. How many eggs did mom have left?

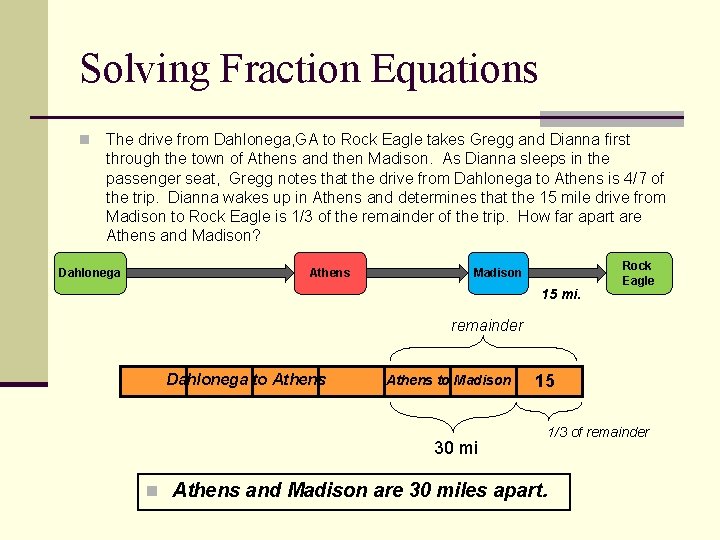
Solving Fraction Equations n The drive from Dahlonega, GA to Rock Eagle takes Gregg and Dianna first through the town of Athens and then Madison. As Dianna sleeps in the passenger seat, Gregg notes that the drive from Dahlonega to Athens is 4/7 of the trip. Dianna wakes up in Athens and determines that the 15 mile drive from Madison to Rock Eagle is 1/3 of the remainder of the trip. How far apart are Athens and Madison? Dahlonega Athens Madison 15 mi. Rock Eagle remainder Dahlonega to Athens to Madison 30 mi 15 1/3 of remainder n Athens and Madison are 30 miles apart.

Solving Fraction Equations -- Practice n Robb’s kids got 240 pieces of candy on Halloween. After performing a “safety check” on the candy, he let his kids keep 3/4 of their haul, took 1/3 of the remainder for “further inspection”, and threw away the rest. How many pieces did he throw away?

Mixture Problems n A “recipe” requires mixing 1 oz of 20% alcohol with 2 oz of 80% alcohol and 5 oz of orange juice. What is the resulting alcohol concentration? 1 oz 20 % 2 oz + 80 % 5 oz + 0% 18/80 = 22 1/2 % The final concentration is 22 1/2 % alcohol 8 oz = ? %

Mixture Problems -- Practice n 2 liters of 30% acid are mixed with 1 gallon of 50% acid. What is the resulting acid concentration?

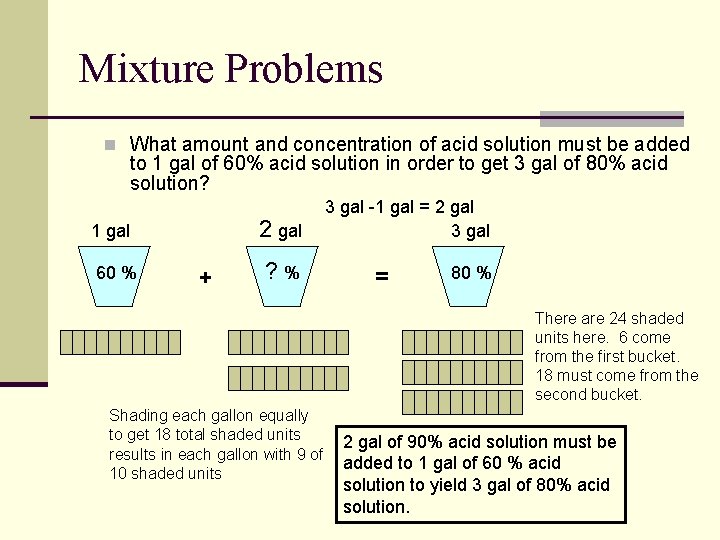
Mixture Problems n What amount and concentration of acid solution must be added to 1 gal of 60% acid solution in order to get 3 gal of 80% acid solution? 2 ? gal 1 gal 60 % + ? % 3 gal -1 gal = 2 gal 3 gal = 80 % There are 24 shaded units here. 6 come from the first bucket. 18 must come from the second bucket. Shading each gallon equally to get 18 total shaded units results in each gallon with 9 of 10 shaded units 2 gal of 90% acid solution must be added to 1 gal of 60 % acid solution to yield 3 gal of 80% acid solution.

Mixture Problems -- Practice n What amount and concentration of acid solution must be added to 2 gal of 30% acid solution in order to get 5 gal of 60% acid solution?

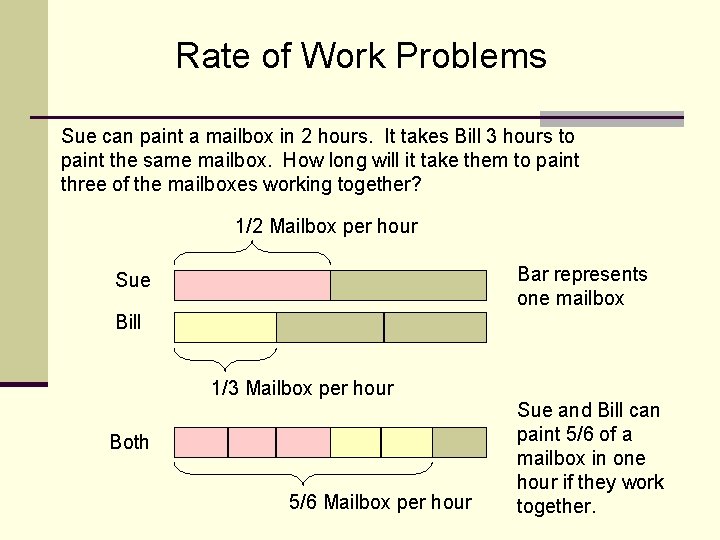
Rate of Work Problems Sue can paint a mailbox in 2 hours. It takes Bill 3 hours to paint the same mailbox. How long will it take them to paint three of the mailboxes working together? 1/2 Mailbox per hour Bar represents one mailbox Sue Bill 1/3 Mailbox per hour Both 5/6 Mailbox per hour Sue and Bill can paint 5/6 of a mailbox in one hour if they work together.

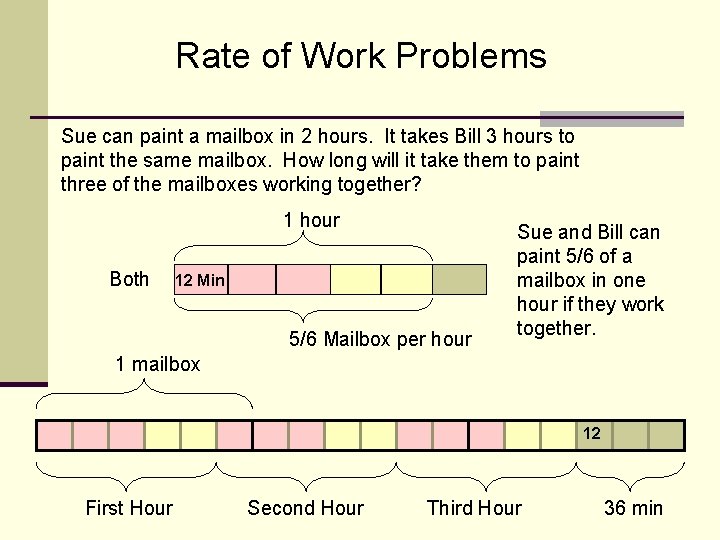
Rate of Work Problems Sue can paint a mailbox in 2 hours. It takes Bill 3 hours to paint the same mailbox. How long will it take them to paint three of the mailboxes working together? 1 hour Both 12 Min 5/6 Mailbox per hour Sue and Bill can paint 5/6 of a mailbox in one hour if they work together. 1 mailbox 12 First Hour Second Hour Third Hour 36 min

Rate of Work Problems -- Practice A pro cyclist can complete a race in 2 hours. A teacher takes 4 hours to complete the same race. If they share a tandem bike, how long will it take them to complete the race pedaling together?

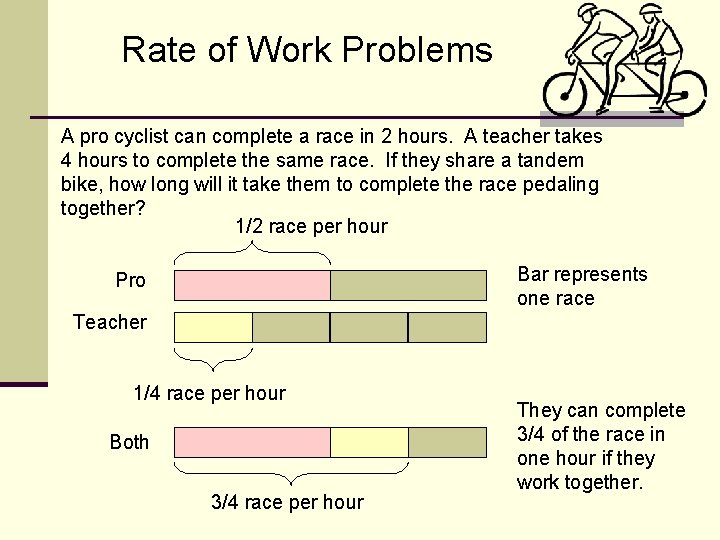
Rate of Work Problems A pro cyclist can complete a race in 2 hours. A teacher takes 4 hours to complete the same race. If they share a tandem bike, how long will it take them to complete the race pedaling together? 1/2 race per hour Bar represents one race Pro Teacher 1/4 race per hour Both 3/4 race per hour They can complete 3/4 of the race in one hour if they work together.

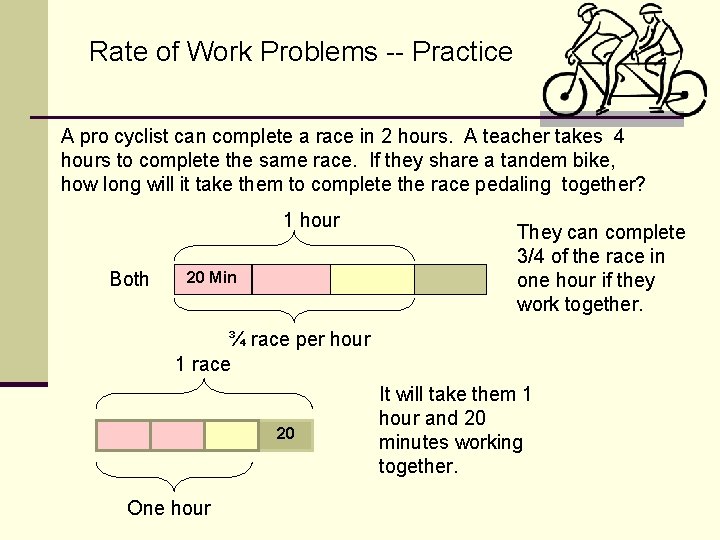
Rate of Work Problems -- Practice A pro cyclist can complete a race in 2 hours. A teacher takes 4 hours to complete the same race. If they share a tandem bike, how long will it take them to complete the race pedaling together? 1 hour Both 20 Min They can complete 3/4 of the race in one hour if they work together. ¾ race per hour 1 race 20 One hour It will take them 1 hour and 20 minutes working together.

Solving Fraction Equations n Robb’s kids got 240 pieces of candy on Halloween. After performing a “safety check” on the candy, he let his kids keep 3/4 of their haul, took 1/3 of the remainder for “further inspection”, and threw away the rest. How many pieces did he throw away? Candy

Solving Fraction Equations n Robb’s kids got 240 pieces of candy on Halloween. After performing a “safety check” on the candy, he let his kids keep 3/4 of their haul, took 1/3 of the remainder for “further inspection”, and threw away the rest. How many pieces did he throw away? Candy 1/4

Solving Fraction Equations n Robb’s kids got 240 pieces of candy on Halloween. After performing a “safety check” on the candy, he let his kids keep 3/4 of their haul, took 1/3 of the remainder for “further inspection”, and threw away the rest. How many pieces did he throw away? 1/3 Candy 1/4

Solving Fraction Equations n Robb’s kids got 240 pieces of candy on Halloween. After performing a “safety check” on the candy, he let his kids keep 3/4 of their haul, took 1/3 of the remainder for “further inspection”, and threw away the rest. How many pieces did he throw away? 1/3 of Remainder Robb’s Candy 240 / 12 =20 Kid’s Candy 20 Thrown Away Candy 3/4 Thrown Away = 20 x 2 = 40 pieces