The Power and Limitations of Statistics in IS

The Power and Limitations of Statistics in IS Research Goal is to ask more questions about IS statistics rather than to blindly accept them…. These Overheads were prepared and made available by Dr. Mary Lacity. 1

The Power and Limitations of Statistics in IS Research • On average, a company’s annual IT operating budget represents 5% of annual revenues. • 80% of IS projects are delivered late and over budget or fail to deliver requirements. • The global IT outsourcing market is $120 billion annually. • There is no discernible relationship between IT investment and productivity. • 6% of US and UK respondents outsource more than 80% of IT budget to third party suppliers. 2

Statistical Concepts Population Parameters and how they are estimated: Census Sample Random Sample Non-random Sample Statistical calculations: Mean (average) Mode Median Standard Deviation Statistical tests: Statistical significance Type I error: alpha value Type II error: beta value correlation t-test 3

Population Census of IS Professionals M M M F F F CENSUS results: Number of Males: Females: M M F F F M M M F F F PARAMETER of Interest: Sex: % of females M M F F F 20 Percentage of Males 50% 20 Females 50% 4

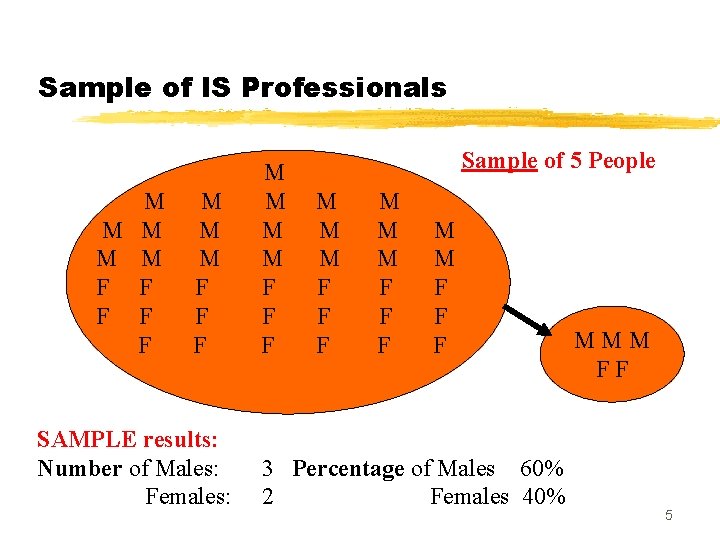
Sample of IS Professionals M M M F F F SAMPLE results: Number of Males: Females: M M F F F Sample of 5 People M M M F F F 3 Percentage of Males 60% 2 Females 40% MMM FF 5

When Sample statistics adequately approximate population parameters: Population Mean Population Variance Population Median Sample mean Sample variance Sample median A sample statistic (such as mean) will be close to a population parameter if: ** Sample size is large enough ** Measuring instrument is good 6 ** Sample is random

IS Professor Salaries: Is the measuring instrument adequate; is the sample random? PARAMETER of Interest: Average IS salary $$$$$$ ? Sample On average, IS professors make $68, 702 7

IS Professor Salaries: Is the measuring instrument adequate; is the sample random? How confident are you in this number? $$$$$$ ? Http: //www. pitt. edu/ galletta/1998 sals. html $68, 702 8

IS Professor Salaries: Is the measuring instrument adequate; is the sample random? How confident are you in this number? $$$$$$ ? Http: //www. pitt. edu/ galletta/1999 sals. html Average: $76, 369 Look at the 1999 survey so far…what can we learn from actually looking at the data!!!!! 9

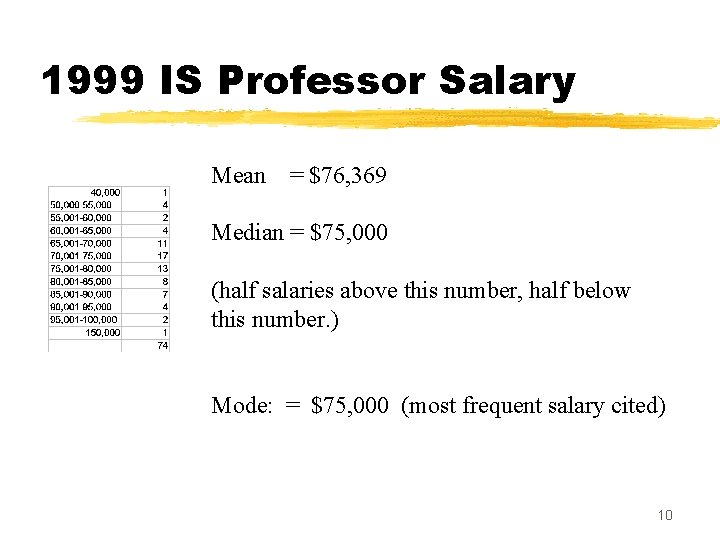
1999 IS Professor Salary Mean = $76, 369 Median = $75, 000 (half salaries above this number, half below this number. ) Mode: = $75, 000 (most frequent salary cited) 10

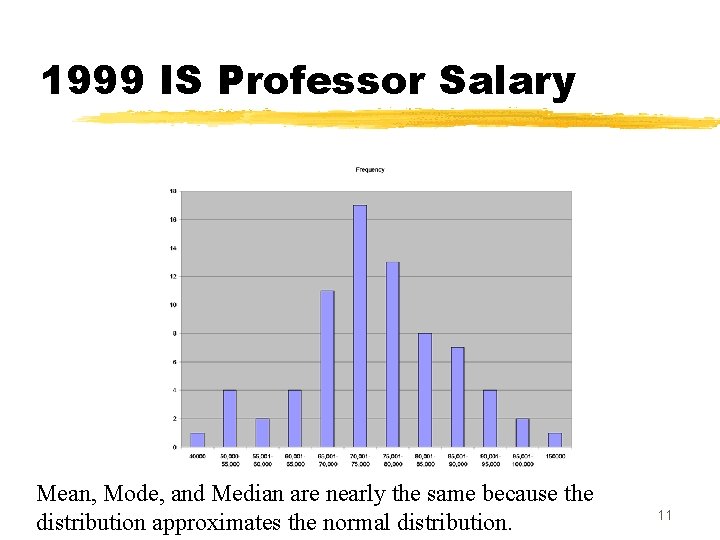
1999 IS Professor Salary Mean, Mode, and Median are nearly the same because the distribution approximates the normal distribution. 11

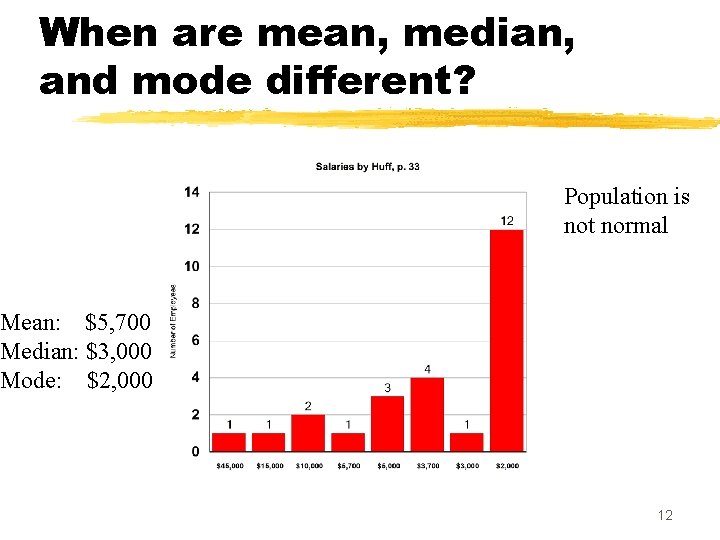
When are mean, median, and mode different? Population is not normal Mean: $5, 700 Median: $3, 000 Mode: $2, 000 12

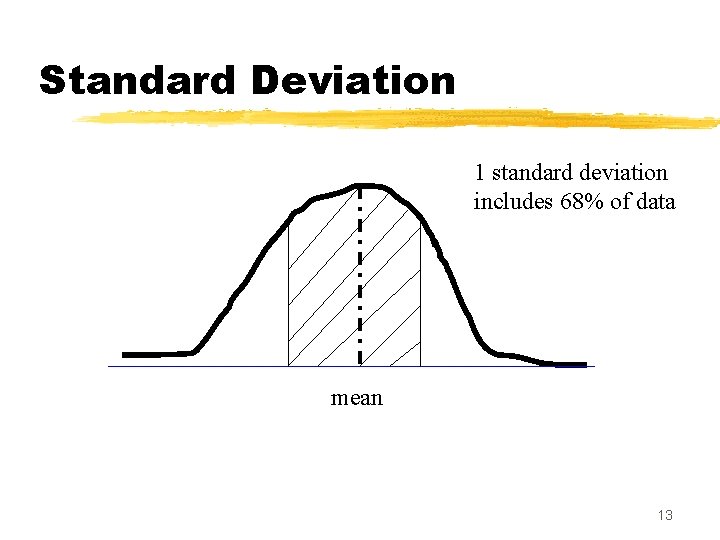
Standard Deviation 1 standard deviation includes 68% of data mean 13

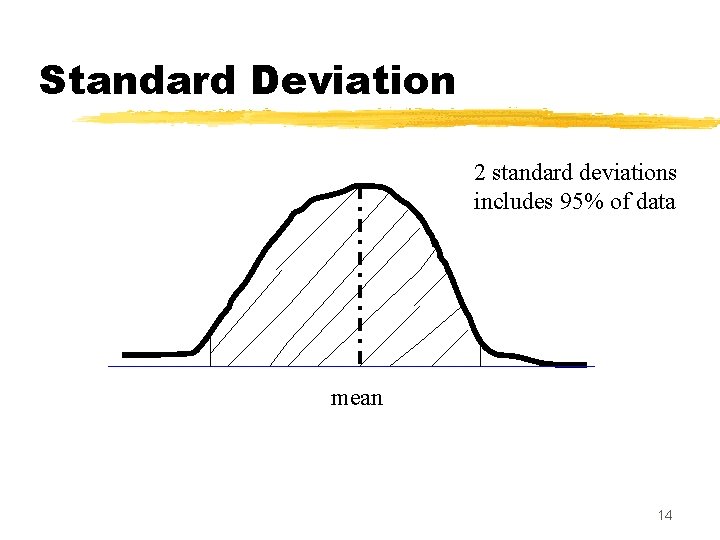
Standard Deviation 2 standard deviations includes 95% of data mean 14

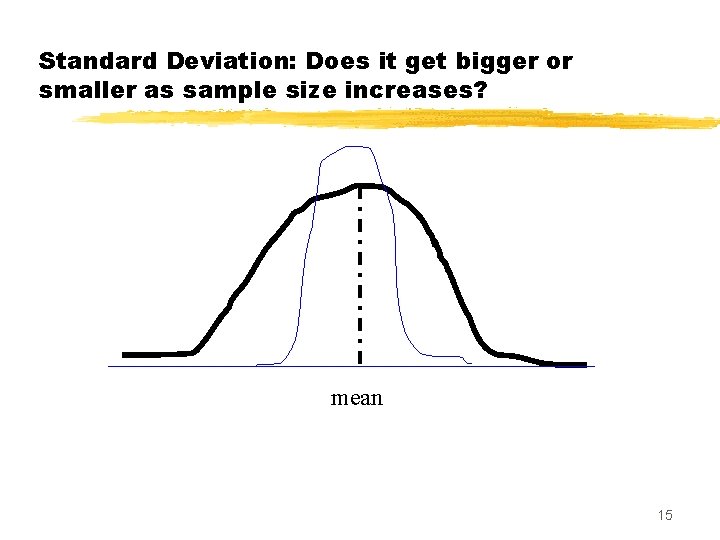
Standard Deviation: Does it get bigger or smaller as sample size increases? mean 15

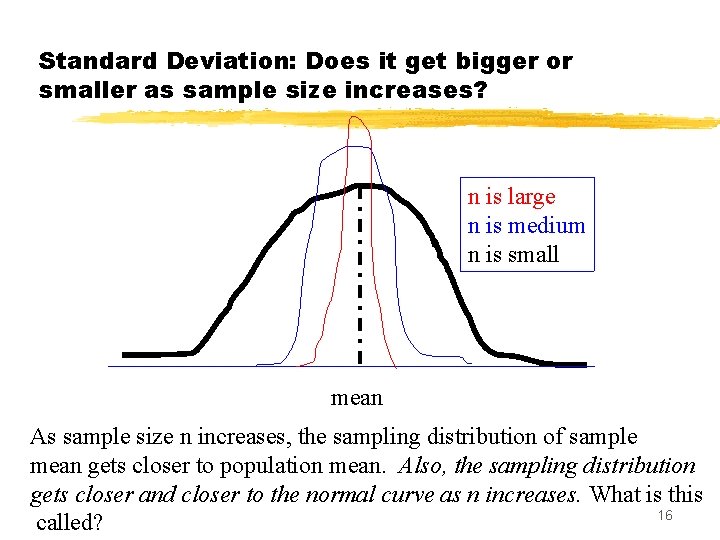
Standard Deviation: Does it get bigger or smaller as sample size increases? n is large n is medium n is small mean As sample size n increases, the sampling distribution of sample mean gets closer to population mean. Also, the sampling distribution gets closer and closer to the normal curve as n increases. What is this 16 called?

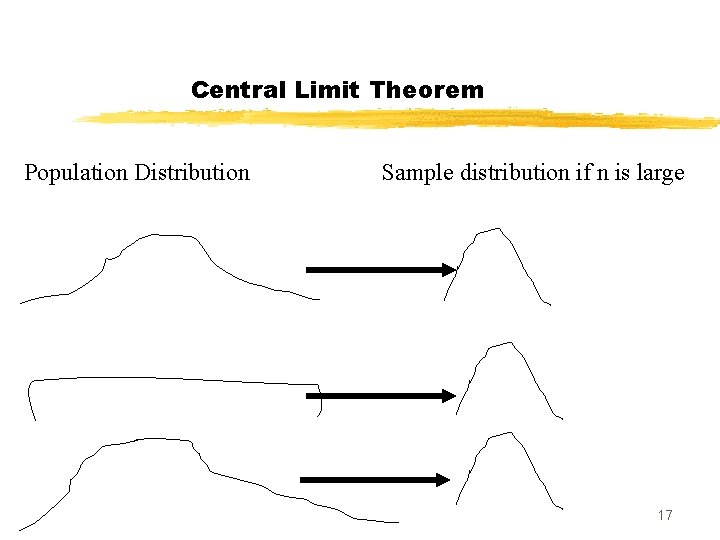
Central Limit Theorem Population Distribution Sample distribution if n is large 17

Type I and Type II Errors Assume this is the real population mean and standard deviation. When we take a sample, we get a sample mean and a sample deviation (or sample error). 18

Type I and Type II Errors Actual Population (which we usually don’t know) Sample 1 Sample 2 19

Type I and Type II Errors Our null hypothesis is: There is no difference between the population mean and sample mean In reality, population does equal sample mean doesn’t = sample mean Sample selected indicates sample mean is different than population mean Sample selected indicates sample mean is same as population mean Type I error No Error No error Type II Error 20

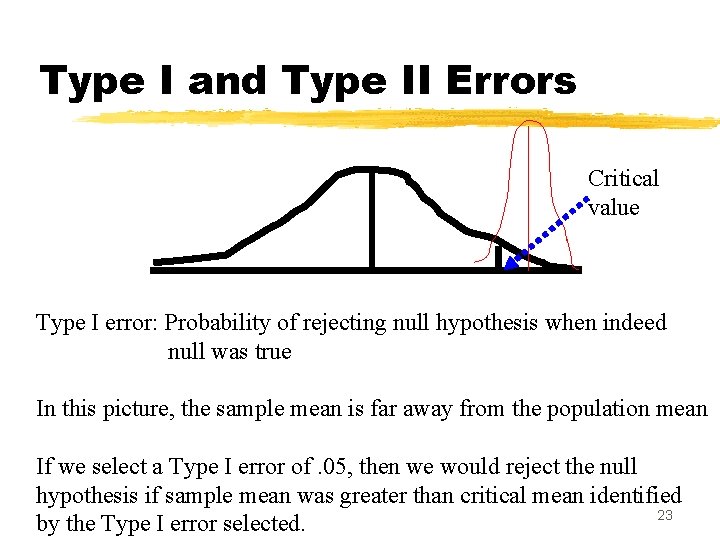
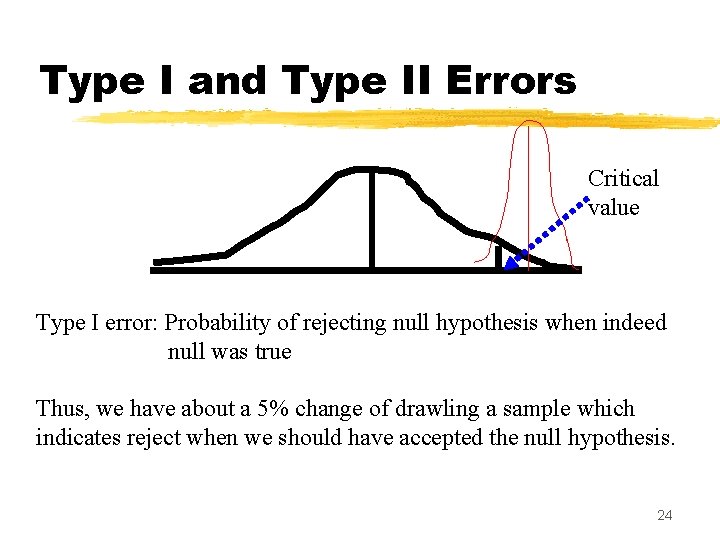
Type I and Type II Errors Type I error: Probability of rejecting null hypothesis when indeed null was true Type II error: Probability of accepting null hypothesis when indeed null was false 21

Type I and Type II Errors Type I error: Probability of rejecting null hypothesis when indeed null was true In this picture, the sample mean is very close to the population mean, so we would get a t-test that is large and indicates: don’t reject the null hypothesis. 22

Type I and Type II Errors Critical value Type I error: Probability of rejecting null hypothesis when indeed null was true In this picture, the sample mean is far away from the population mean If we select a Type I error of. 05, then we would reject the null hypothesis if sample mean was greater than critical mean identified 23 by the Type I error selected.

Type I and Type II Errors Critical value Type I error: Probability of rejecting null hypothesis when indeed null was true Thus, we have about a 5% change of drawling a sample which indicates reject when we should have accepted the null hypothesis. 24

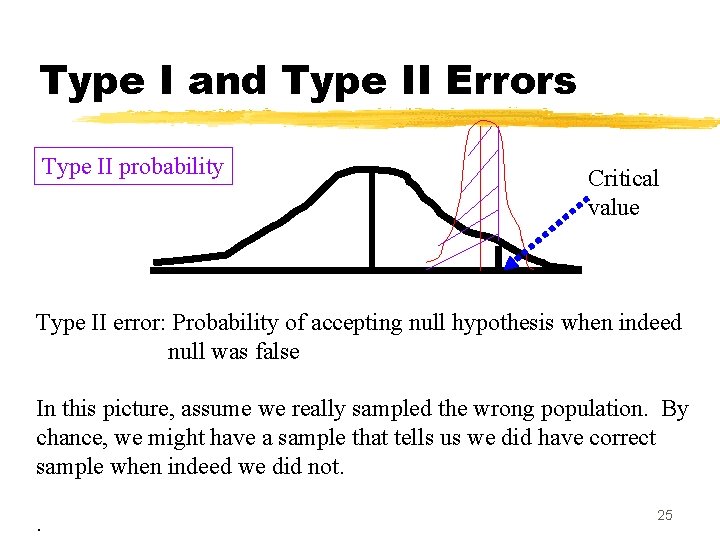
Type I and Type II Errors Type II probability Critical value Type II error: Probability of accepting null hypothesis when indeed null was false In this picture, assume we really sampled the wrong population. By chance, we might have a sample that tells us we did have correct sample when indeed we did not. . 25

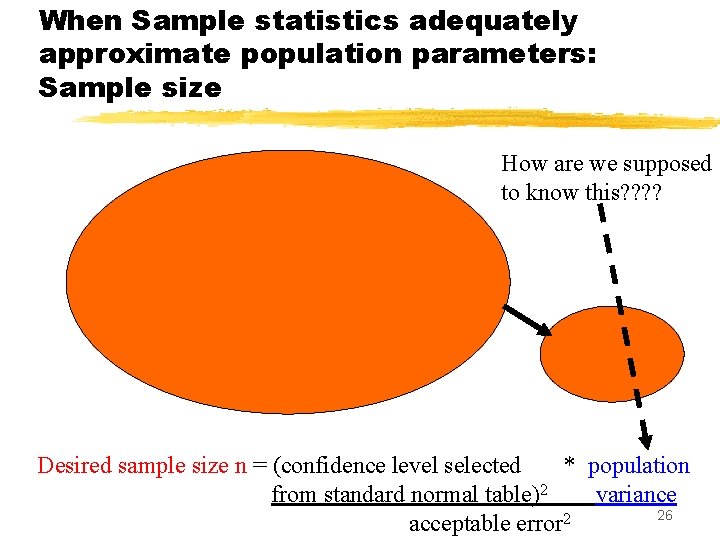
When Sample statistics adequately approximate population parameters: Sample size How are we supposed to know this? ? Desired sample size n = (confidence level selected * population from standard normal table)2 variance 26 acceptable error 2

When Sample statistics adequately approximate population parameters: Sample size: An example Assume we want to take a sample of IS professor salaries and assume we know the standard deviation is $12, 000. If we will accept a plus or minus $3, 000 error, how large should the sample be? Desired = (confidence level selected * population sample size n from standard normal table)2 variance acceptable error value 2 n = (1. 96)2 * (12, 000)2 $3, 0002 n = ? ? 27

28 28

The semi-attached figure: Which country has highest cell phone adoption rate? 29

The semi-attached figure: Which Internet Stock should I invest in? 30

The One Dimensional Picture Excite Msn. com had twice as many visitors as Excite. com 31

So where did this statistic come from? ? ? On average, a company’s annual IT budget represents 5% of annual revenues It was a generally quoted statistic I heard over and over again. One example includes: Minoli, Analyzing Outsourcing, Re-engineering Information And Communication Systems, Mc. Graw Hill, 1994. Data collected by author, but not much detail is given. My confidence comes from the fact that his results are similar to many other results from studies I’ve seen. 32

So where did this statistic come from? ? ? 80% of IS projects are delivered late and over budget or fail to deliver requirements. It was a generally quoted statistic I heard over and over again. Some more formal studies found: AUTHOR # of Projects Lehman 1979 57 Gladden 1982 ? ? ? Johnson 1995 365 Phan (1995) 143 FINDINGS 46% overdue; 59% over budget 75% systems not used or not completed 31% projects cancelled; 53% cost over-run; 12% delivered on time to budget 25% do not meet requirements 33

So where did this statistic come from? ? ? The global IT outsourcing market is $120 billion annually This statistic was reported by International Data Corporation on http: //www. outsourcing. com last year. However, sit no longer exists. I found the following quote on: http: //www. infoserver. com/. . [5]. src = "images/news_faq_up. gif"; } // --> Company: PR Newswire Date of Post: 08 -Aug-99 Type of Article: Market Trends Article Title: IDC Reports Worldwide Outsourcing Spending Approached $100 Billion in 1998 and Will Surge to Over $151 Billion by 2003 Summary: Worldwide outsourcing services. . . 34

So where did this statistic come from? ? ? There is no discernible relation between IT investment and productivity. Attempts to correlate investments in information technology to productivity have found no correlation or a negative correlation: ·A study of 60 manufacturing firms during the period of 1974 -1984 failed to show a · significant positive relationship between IT expense and productivity. ·A study of 58 mutual savings banks found no relationship between organizational · performance and IT expense. ·An evaluation by the US Department of Commerce for the years 1950 -1986 show · a negative correlation between information technology and productivity. 35

So where did this statistic come from? ? ? There is no discernible relation between IT investment and productivity. ·A research report by the Gartner Group revealed that firms that invested in ·office automation systems had exactly the same level of productivity in 1987 as they did in 1967. ·Japan and Europe have much higher office and service sector productivity ·than the US even though they have not computerized nearly as quickly as the US ·Peter Drucker observed that the number of office workers and clerical staff · grow in proportion to investments in information technology. 36

So where did this statistic come from? ? ? There is no discernible relation between IT investment and productivity. ·How can the paradox be correct? ·The paradox runs counter to intuition. ·We see the effects on productivity everyday--automated tellers, laser checkouts, fax machines, word processors, travel reservation systems. 1. Macroeconomic studies have no internal validity because the information technology/productivity paradox merely captures a correlation, not a causal relationship. Perhaps productivity would have suffered a major decline without investments in IT. 37

So where did this statistic come from? ? ? There is no discernible relation between IT investment and productivity. 2. Macroeconomics considers worker productivity, not net benefits to society. For example, automated tellers may not correlate with higher banking productivity, but society as a whole benefits from convenient, 24 -hour banking. 3. IT is like R&D, many projects will fail, but you only need a few to gain a big payoff. 38

So where did this statistic come from? ? ? There is no discernible relation between IT investment and productivity. 4. Quinn & Baily outline flaws with macroeconomic numbers: ·Industry productivity only captures 42% of service sector employment · 30% of the productivity figures equate output and input --which will be constant! Example: Input is budget, Output assumes an equivalent $ value for input. For example, if the police department’s budget is $5 million, it assumes they produced $5 million worth of law enforcement. 39

So where did this statistic come from? ? ? • 6% of US and UK respondents outsource more than 80% of IT budget to third party suppliers. This statistic came from a survey that Leslie Willcocks and I administered to the following sample: For US survey, 500 names of CIOs were obtained from a list maintained by Dun & Bradstreet Information Services. Only 38 people returned the survey. For UK survey, a list of 100 CIOs were compiled from various sources including Financial Times top 100 list, and members of the Oxford Institute of Information Management. 63 surveys 40 were returned from UK.

So where did this statistic come from? ? ? How confident are we in this 6% number? Other surveys (which will have their own biases and limitations, found a similarly low number of total outsourcing; most companies pursue selective sourcing: In a survey of 300 IT managers in the US, on average less than 10% of the IT budget was outsourced (Caldwell, 1996 a) A survey of 110 Fortune 500 companies found that 76% spent less than 20% of the IT budget on outsourcing, and 96% spent less than 40% (Collins and Millen, 1995) A survey of 365 US companies found that 65% outsourced one or more 41 IT activities, but only 12 outsourced IT completely (Dekleva, 1994)

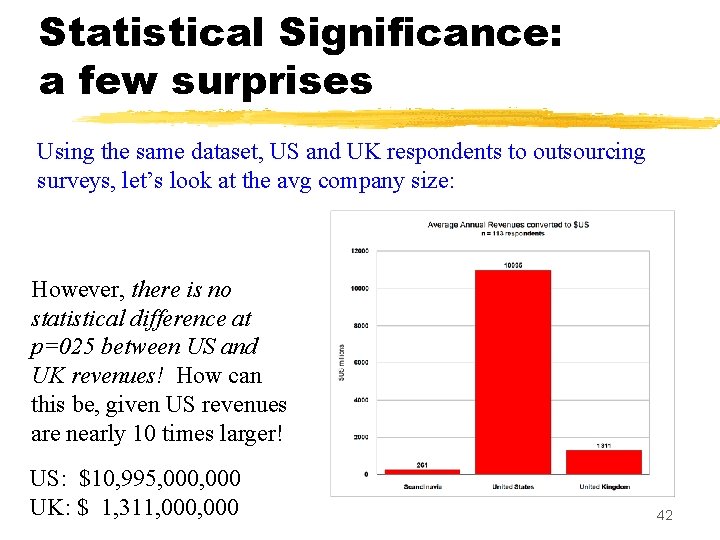
Statistical Significance: a few surprises Using the same dataset, US and UK respondents to outsourcing surveys, let’s look at the avg company size: However, there is no statistical difference at p=025 between US and UK revenues! How can this be, given US revenues are nearly 10 times larger! US: $10, 995, 000 UK: $ 1, 311, 000 42

Look at the standard deviation! Minimum Maximum Average Standard Deviation $US Revenues UK revenues in $US $30 million $168, 800 million $12, 000 million $10, 995 million $1, 311 million $29, 158 million $2, 728 million “Despite differences in means, a one-tailed t-test assuming heteroscedasticity at p=. 025 level indicates that US and UK revenues are not statistically different. This finding is explained by the large standard deviation. 43

44

Gotta!!!! The key is the level of significance for the probability of a type I error. Type I error = probability that we reject the null hypothesis when indeed the null is true. With a t-test, we are testing the null hypothesis that the US and UK revenues not different. At a selected p=. 025, we are saying that we want the probability of rejecting the null hypothesis if indeed the null is true to be. 025. 45

Gotta!!!! In reality, the calculated p value was. 03 Thus, if our selected p value is. 025, we only reject the null hypothesis if the calculated p value was less than. 025. Thus I can conclude that US and UK revenues are different at. 025 level. What do we conclude if selected probability of type I error is. 05, the more usual probability selected? 46

Conclusions “How to talk back to a statistic”, Huff, 1982, pp. 122 -142 Who says so? How does he know? Did Somebody Change the subject? Does It Make Sense? 47