The potential difference across the capacitor DVC QC

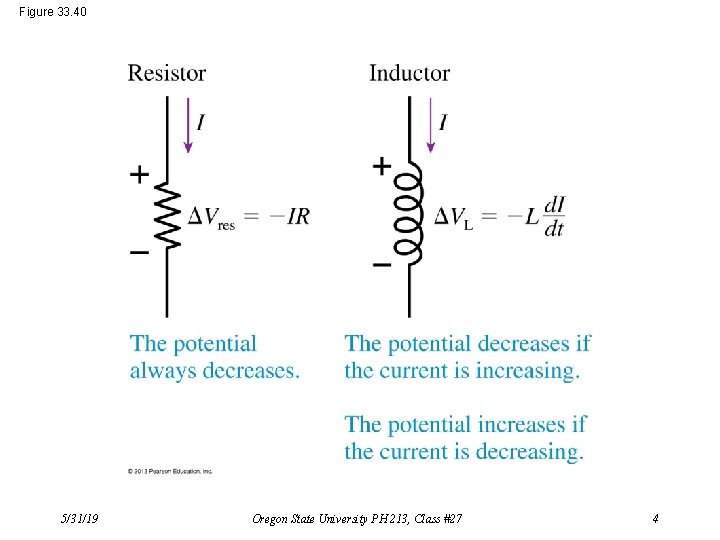
The potential difference across the capacitor: DVC = (±)Q/C The capacitor’s ability to store energy: UC = (1/2)C(DVC)2 The potential difference across the inductor: DVL = –L(d. I/dt) The inductor’s ability to store energy: 5/31/19 Oregon State University PH 213, Class #27 UL = (1/2)L(I)2 1

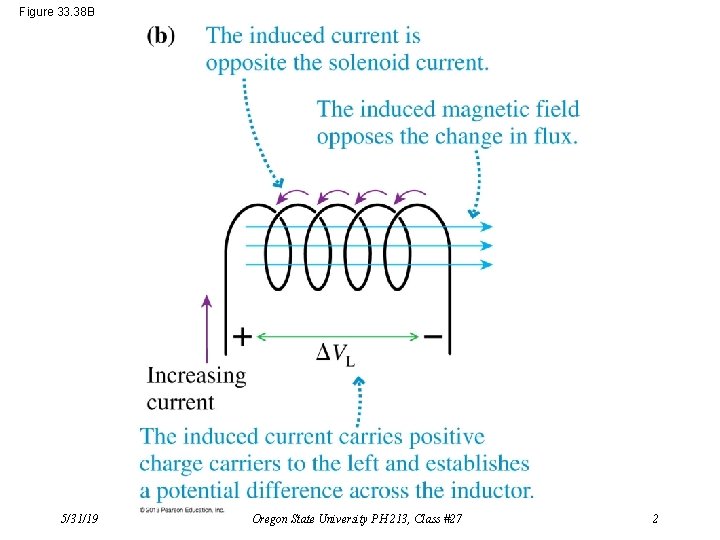
Figure 33. 38 B 5/31/19 Oregon State University PH 213, Class #27 2

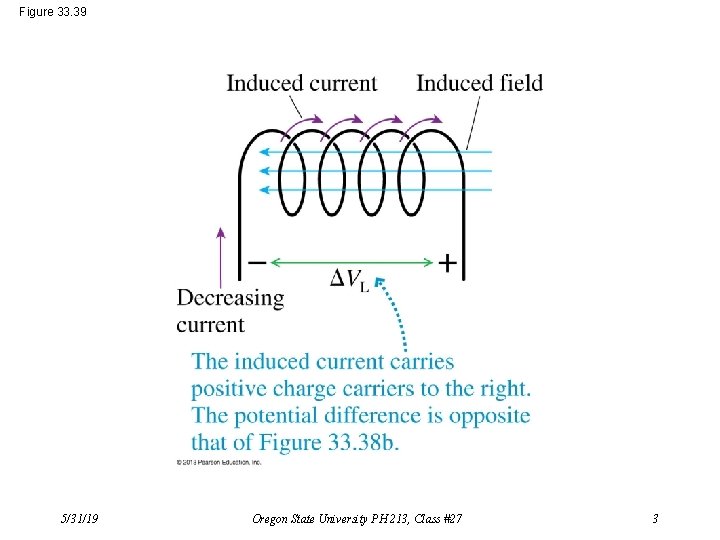
Figure 33. 39 5/31/19 Oregon State University PH 213, Class #27 3

Figure 33. 40 5/31/19 Oregon State University PH 213, Class #27 4

The potential at a is higher than at b. Which of these statements about the inductor current I could be true? A. B. C. D. E. F. 5/31/19 I is from a to b and is steady. I is from a to b and is increasing. I is from a to b and is decreasing. I is from b to a and is steady. I is from b to a and is increasing. I is from b to a and is decreasing. Oregon State University PH 213, Class #27 5

Applications of Inductors There are several common uses for inductors in circuits (mainly with ac—alternating current—sources, but we can understand their basic principles without getting much into ac): Oscillations (LC circuit) (good for signal transmissions; resonance) Controlled current rise/fall (good for frequency filtering) 5/31/19 (LR circuit) Oregon State University PH 213, Class #27 6

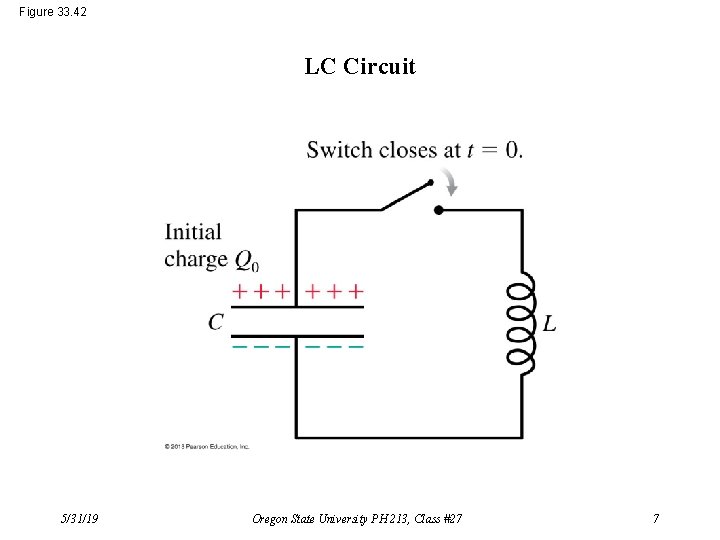
Figure 33. 42 LC Circuit 5/31/19 Oregon State University PH 213, Class #27 7

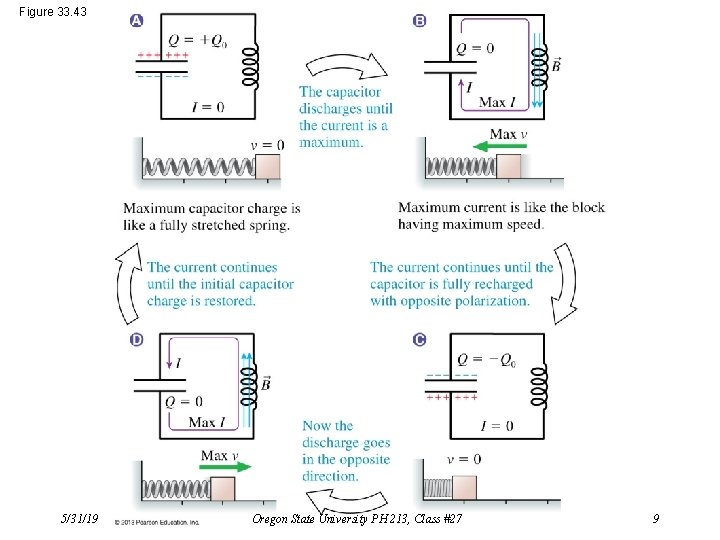
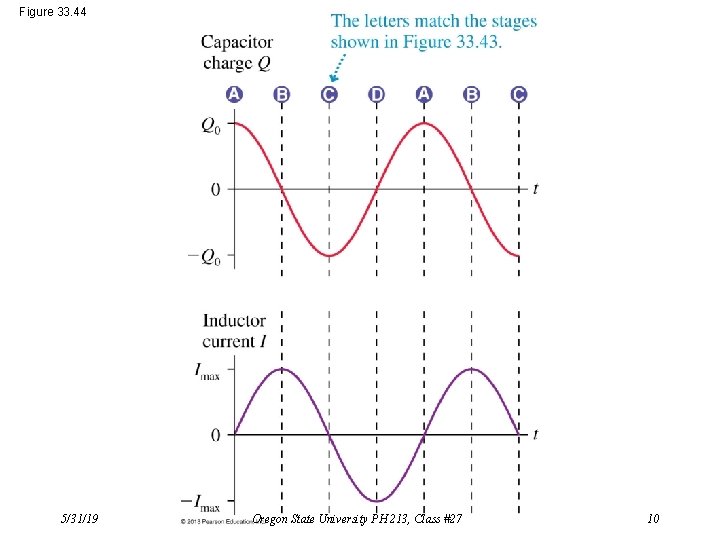
LC Circuit DVC + DVL = 0 Kirchhoff’s Loop Rule: That is: Resulting differential equation: Q/C – L·d. I/dt = 0 d 2 Q/dt 2 = –[1/(LC)]Q We recognize the solution to this: It’s a harmonic oscillator with angular frequency, w = √[1/(LC)]. That is: Q(t) = Q 0 cos(wt) Then note: 5/31/19 [assumes Q 0 = Q(0)] I(t) = –d. Q/dt = w. Q 0 sin(wt) = Imaxsin(wt) Oregon State University PH 213, Class #27 8

Figure 33. 43 5/31/19 Oregon State University PH 213, Class #27 9

Figure 33. 44 5/31/19 Oregon State University PH 213, Class #27 10

Quick check: If you start at t = 0 with all charge on the capacitor of an LC circuit: After how much time (given in terms of T, the period), will the current in the inductor be at maximum magnitude? After how much time will the current switch directions? 5/31/19 Oregon State University PH 213, Class #27 11

In an LC circuit oscillating at a frequency of 1000 Hz, the maximum charge on the capacitor is 1. 00 m. C. What is the maximum current through the inductor? If the capacitance value is 1 µF, what is the inductance value? 5/31/19 Oregon State University PH 213, Class #27 12

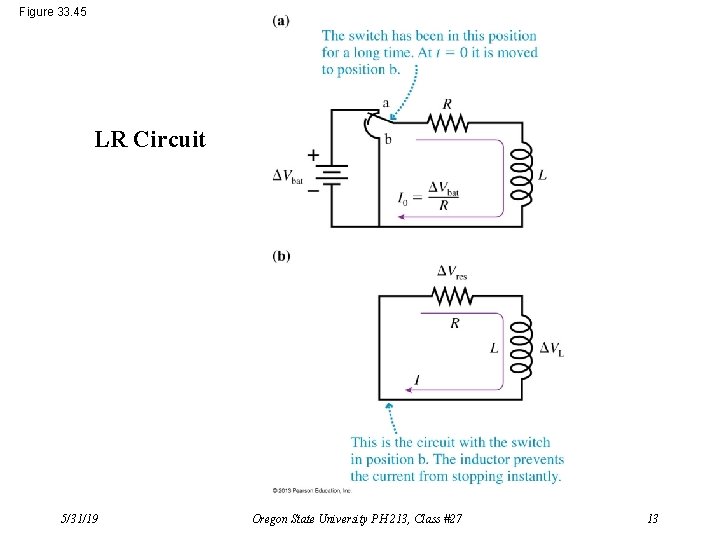
Figure 33. 45 LR Circuit 5/31/19 Oregon State University PH 213, Class #27 13

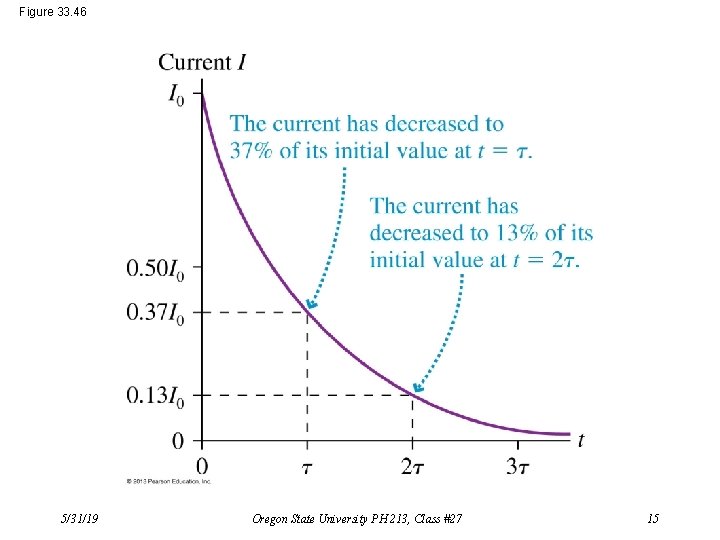
LR Circuit (Current Decay) Kirchhoff’s Loop Rule: That is: DVR + DVL = 0 –IR – L·d. I/dt = 0 Resulting differential equation: d. I/I = dt/(L/R) We recognize the solution to this: It’s an exponential decay, where the decay’s time constant, t = L/R. That is: I(t) = I 0 e–t/(L/R) And: 5/31/19 DVL(t) = –DVR = I 0 Re–t/(L/R) Oregon State University PH 213, Class #27 14

Figure 33. 46 5/31/19 Oregon State University PH 213, Class #27 15

LR Circuit (Current Rise) Kirchhoff’s Loop Rule: e + DVR + DVL = 0 I(t) = Imax[1 – e–t/(L/R)] = (e/R)[1 – e–t/(L/R)] And: 5/31/19 DVL(t) = –e – DVR = –e + IR = –ee–t/(L/R) Oregon State University PH 213, Class #27 16

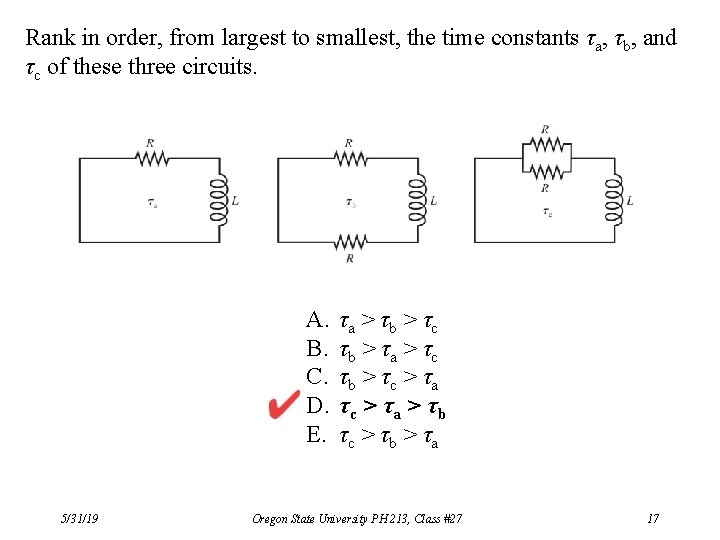
Rank in order, from largest to smallest, the time constants τa, τb, and τc of these three circuits. A. B. C. D. E. 5/31/19 τa > τb > τc τb > τa > τc τb > τc > τa > τb τc > τb > τa Oregon State University PH 213, Class #27 17

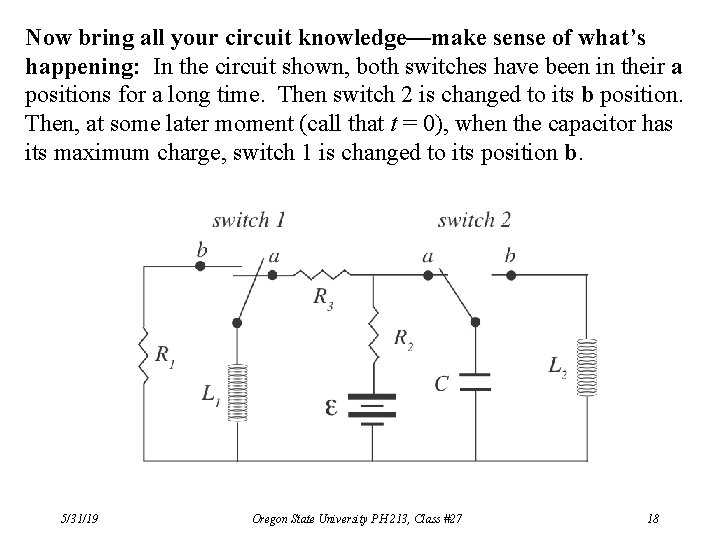
Now bring all your circuit knowledge—make sense of what’s happening: In the circuit shown, both switches have been in their a positions for a long time. Then switch 2 is changed to its b position. Then, at some later moment (call that t = 0), when the capacitor has its maximum charge, switch 1 is changed to its position b. 5/31/19 Oregon State University PH 213, Class #27 18