The Polynomial Method In Quantum and Classical Computing

The Polynomial Method In Quantum and Classical Computing OP EN Scott Aaronson (MIT) PR OB LEM

Overview The polynomial method: Just an awesome tool that every CS theorist should know about Goes back to the prehistory of the field (1960’s), but also plays a major role in current work [including at this FOCS] on machine learning, quantum computing, circuit lower bounds, communication complexity… Idea: Reduce CS questions to questions about the minimum degree of real polynomials Easy to learn! “Look ma, no quantum”

This Talk: Just Some Basics 1. Polynomials in machine learning - Perceptrons 2. Polynomials in quantum computing Stuff I -wish I could cover but can’t lack algorithms of time Optimality of Deutsch-Jozsa andfor Grover - Polynomials finite fields (Razborov-Smolensky) - Collisionover lower bound - Reduction of communication problems to polynomials 3. - Sherstov’s Polynomials in circuit complexity pattern matrix method - Deep - Linial-Mansour-Nisan connections to Fourier and analysis Bazzi 4. Polynomials everywhere! - Communication complexity, oracles, streaming…

Our story starts in St. Petersburg, around 1889… привет! I proved a cool theorem: if pyou’re is a quadratic, Uhh … on your own And what if p has degree d? Dmitri Mendeleev A. A. Markov (periodic table dude) (inequality dude)

Markov did generalize Mendeleev’s bound to arbitrary degree (about which more later) He thereby helped start a field called approximation theory Approximation theory is a proto-complexity theory! Real polynomials = Model of computation Degree = Complexity measure So, maybe not so surprising that it ends up being related to actual complexity theory…

1. POLYNOMIALS IN MACHINE LEARNING

Fast-forward to 1969… And AI researchers were studying perceptrons f f 1 f 2 … Bill Ayers was working for the Mc. Cain’ 08 campaign fm A perceptron of order k is a Boolean function f: {0, 1}n {0, 1} that’s a threshold of subfunctions on at most k variables each

Minsky and Papert: Small perceptrons have serious limitations! Application: “killed neural net research for a decade” Suppose f: {0, 1}n {0, 1} is represented by an order-k perceptron Then there’s clearly a degree-k polynomial p: Rn R such that for all x 1, …, xn {0, 1}, Furthermore, without loss of generality p is multilinear: no variable raised to higher power than 1

Example: The PARITY function Suppose for all x 1, …, xn {0, 1}. Then what can we say about deg(p)? Theorem: deg(p) n Key idea: Symmetrization Replace multivariate polynomials by univariate ones, which are easier to understand

How Symmetrization Works Let Key Lemma: q(k) is itself a polynomial in k, of degree at most d

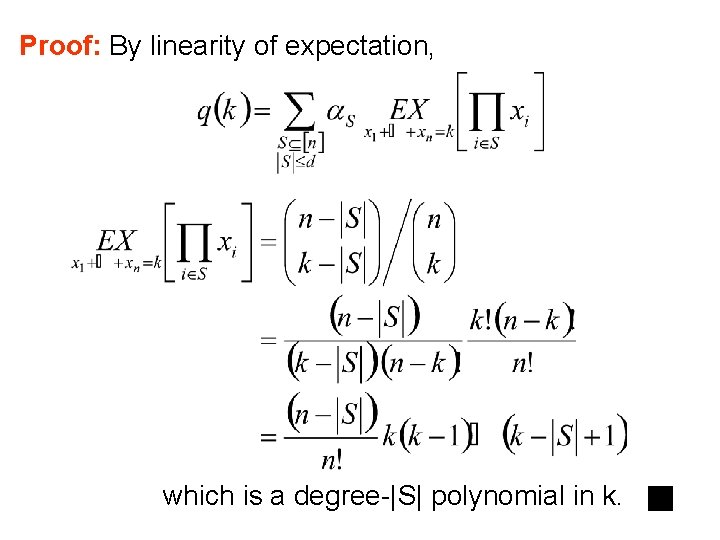
Proof: By linearity of expectation, which is a degree-|S| polynomial in k.

So, suppose there’s an order-k perceptron computing the parity of n bits Then there’s a degree-k multilinear polynomial p such that Hence there’s a degree-k univariate polynomial q such that for all k=0, …, n, Must have degree n

2. POLYNOMIALS IN QUANTUM COMPUTING

Quantum Query Model In One Slide What are the allowed operations? Initialize vector of amplitudes Query the input bits Quantum state: Unit vector in Cn One further detail: The quantum state can have more a than n dimensions, with multiple“Measure” components Apply unitary transformation querying each xi, as well as components that don’t make queries at all Outcome i observed with probability | i|2 Complexity Measure: Q(f) = minimum number of queries needed to compute a Boolean function f with probability 2/3, on all inputs x=x 1…xn

Example: The Deutsch-Jozsa Algorithm Does something spectacular: Computes the XOR of two bits with one oracle call! By computing x 1 x 2, x 3 x 4, etc. , can compute the parity of n bits with n/2 oracle calls Is that optimal?

Lemma (Beals et al. 1998): If a quantum algorithm makes T queries, its probability of accepting is a degree-2 T multilinear polynomial over the xi’s Right-to-Left Proof: Implication: If a quantum algorithm computed x 1 xn with <n/2 queries, it would lead to a polynomial approximating PARITY with degree <n. Entries After are Deutsch-Jozsa now TStill queries, Degree-2 degree-1 degree-T polynomials over the xi’s Hence must be optimal! Then has degree 2 T

Another Famous Quantum Algorithm: Grover’s Computes the OR of n bits using O( n) queries Is Grover’s algorithm optimal? BBBV 1994: Yes, by a quantum argument We’ll instead prove Grover is optimal using … wait for it …

Given a Boolean function f, let deg (f) be the minimum degree of a real polynomial p: Rn R such that Theorem (Nisan-Szegedy 1994): Observation: Is that lower bound tight? Yes, because of Grover’s algorithm!

To prove deg (OR)= ( n), we need to revisit our good friend Markov… Theorem (Markov): If p is a degree-d real polynomial, then Another convenient form: for all n>0,

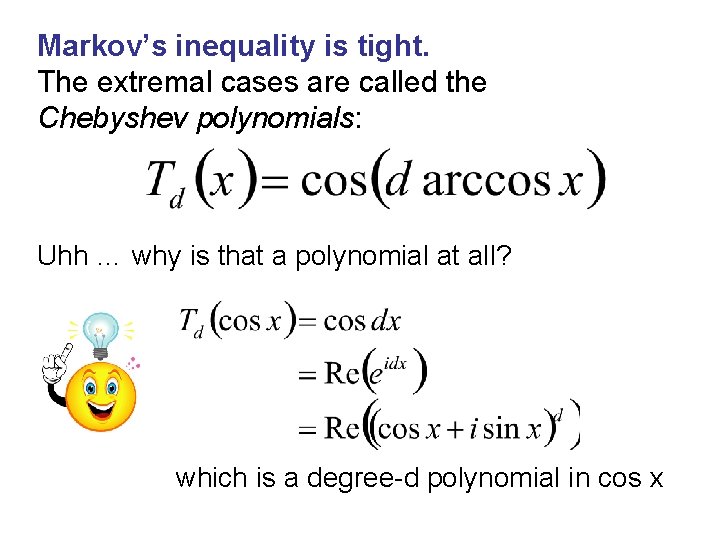
Markov’s inequality is tight. The extremal cases are called the Chebyshev polynomials: Uhh … why is that a polynomial at all? which is a degree-d polynomial in cos x

Let p satisfy We want to lower-bound deg(p) Symmetrize: 1 0

1 So by Markov’s inequality, 0 One remaining problem: q(x) need not be bounded at non-integer x Solution: Notice

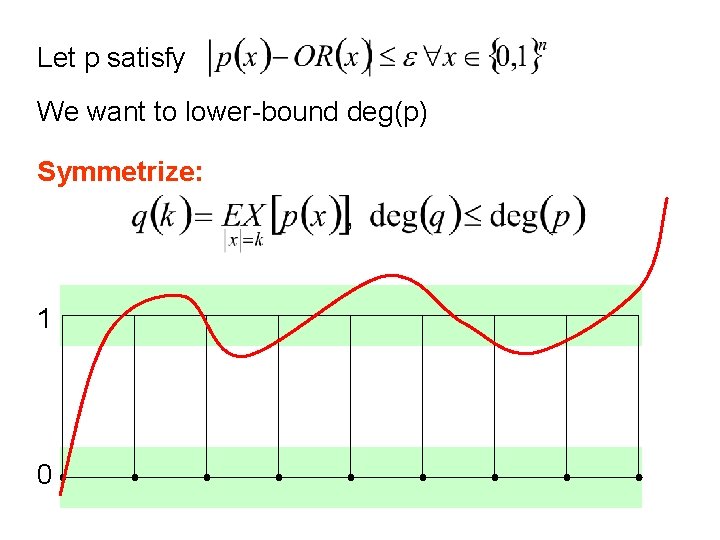
Collision Problem Illustrates the amazing reach of the polynomial method Problem: Given f: [n], decide whether f is 1 -to-1 or 2 -to-1, promised it’s one or the other By the Birthday Paradox, ~ n queries to f are necessary and sufficient classically [Brassard et al. 1997] gave a quantum algorithm making O(n 1/3) queries [A. 2002]: Any quantum algorithm needs (n 1/5) queries. Improved to (n 1/3) by Shi

Lower bound by polynomial method Let Lemma (following Beals et al. ): If a quantum algorithm makes T queries to f, the probability p(f) that it accepts is a degree-2 T polynomial in the (x, h)’s Now let be the expected acceptance probability on a random k-to-1 function

The Miracle: q(k) is itself a polynomial in k, of degree at most 2 T

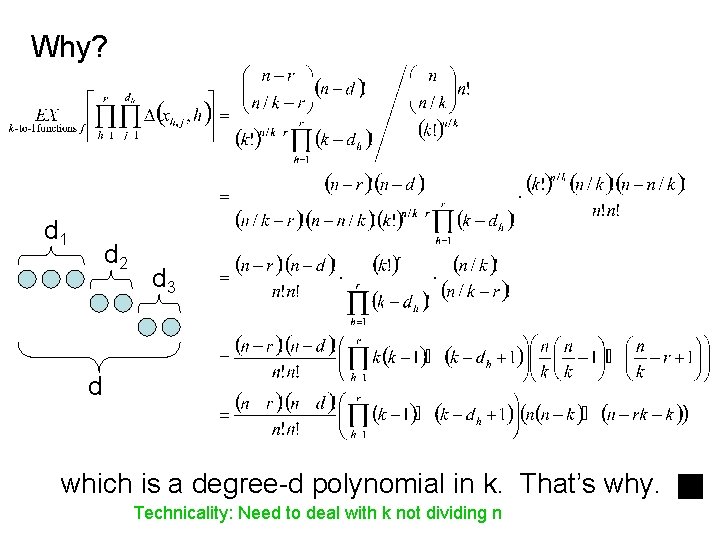
Why? d 1 d 2 d 3 d which is a degree-d polynomial in k. That’s why. Technicality: Need to deal with k not dividing n

Another Useful Hammernomial: Bernstein’s Inequality Application: Any quantum algorithm to compute the MAJORITY of n bits requires (n) queries Ouch, that really hurts the degree!

Oh, and don’t forget the inequality of V. A. Markov—A. A. ’s younger brother! Application [A. 2004]: Direct product theorem for quantum search. After T queries, the probability that a quantum algorithm finds K marked items out of N is at most (c. T 2/N)K 0 1 K N

3. POLYNOMIALS IN CIRCUIT COMPLEXITY

Linial-Mansour-Nisan 1993: If a Boolean function f is computable by an AC 0 circuit of size s and depth k, then we can find a degree-d real polynomial p such that Proof uses the Switching Lemma to upper-bound high-degree Fourier coefficients By Nisan-Szegedy, the above theorem would be false if we wanted |p(x)-f(x)| to be small for every x

Bazzi 2007: Let F=C 1 Cm be a DNF formula. Then we can find degree-d real polynomials p and q such that Implies that polylog-wise independent distributions “fool” small DNFs. The proof takes 64 8] 0 0 2 v o r [Razbo pages

4. POLYNOMIALS EVERYWHERE

Polynomials in Oracle-Building Beigel 1992: There exists an oracle relative to which PNP PP Use the following problem: Given exponentially-long integers x=x 1…x. N and y=y 1…y. N, is x y? It’s in PNP, since we can use binary search to find the leftmost i such that xi yi But is there a low-degree polynomial p such that

Sure: But by clever repeated use of Markov’s inequality, one can show that any such polynomial must take on huge (doubly-exponentially-large) values This means the problem can’t be in PP [A. 2006] generalized Beigel’s result to give an oracle relative to which PP has linear-size circuits Requires handling many polynomials simultaneously

Slide of Guilt: The Polynomial Method in Communication Complexity Razborov 2002: Any quantum protocol for the Disjointness problem requires ( n) qubits of Razborov and Sherstov, this very FOCS: communication An AC 0 function with large unbounded-error communication complexity Sherstov, this very FOCS: Characterizes the unboundederror communication complexity Chattopadhyay-Ada, Lee-Shraibman 2008: Lower of symmetric functions bounds for the k-party communication complexity of Disjointness in the Number-On-Forehead And model more!

Some Positive Uses of Polynomials Harvey-Nelson-Onak, this very FOCS: Chebyshev polynomials used to give a streaming algorithm for approximating the Shannon entropy Beigel-Reingold-Spielman 1991: PP is closed under intersection

Future Direction 1: Beyond Symmetrization Find better techniques to lower-bound the degrees of multivariate polynomials. OR Upper bound: O( n) n AND AND n (from quantum algorithm) Lower bound: (n 1/3) (can be proved using the n 1/3 collision lower bound) deg(f)=O(deg (f)2) for all Boolean functions f? Best known relation: deg(f)=O(deg (f)6) (Beals et al. )

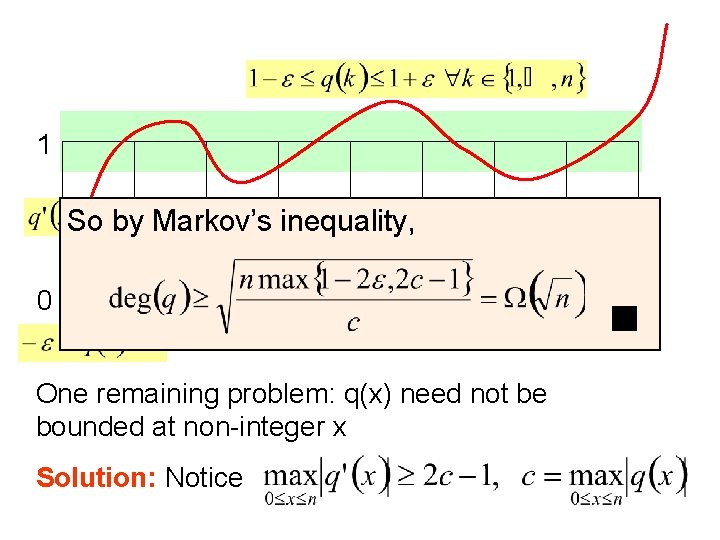
Future Direction 2: Understanding Bounded Real Polynomials Conjecture. Let p: Rn [0, 1] be a real polynomial of degree d. Suppose EXx, y[|p(x)-p(y)|]= (1). Then there exists an i [n] such that EXx[|p(x)-p(xi)|]= (1/poly(d)). Would have major implications for quantum! e. g. , for P vs. BQP relative to a random oracle Given a partial function f: S {0, 1} (S {0, 1}n), let deg (f) be the minimum degree of a polynomial p such that (1) 0 p(x) 1 for all x {0, 1}n, (2) |p(x)-f(x)| for all x S. Is there a partial f for which deg (f) is exponentially smaller than Q(f)?

Future Direction 3: Matrix- Valued Polynomials What Boolean functions can we approximate as Would imply an oracle relative to which SZK QMA (i. e. , “there are no succinct quantum proofs for problems like graph non-isomorphism”) Conjecture. Suppose max(A(x)) [0, 1] for all x {0, 1}n max(A(x)) 2/3 for all x encoding a 1 -to-1 function max(A(x)) 1/3 for all x encoding a 2 -to-1 function Then d 2(d+log m)= (n).

Future Direction 4: Extending Bazzi’s Theorem to AC 0 (the Linial-Nisan Conjecture) Problem: Given f AC 0, construct polylog(n)-degree polynomials p, q: Rn R such that If p, q have the further property that then we get an oracle relative to which BQP PH.

The polynomial method: the choice of hardworking American lowerboundsmen I approve! OPEN PROBLEM