The Polynomial Hierarchy 7 3 2 Enumeration Problems

The Polynomial Hierarchy 7. 3. 2 Enumeration Problems 7. 3. 3 R. Anderson, S. Dugginapeddi, and V. Gadde

7. 3. 2 POLYNOMIAL HIERARCHY

Polynomial Hierarchy • • Class co. NP NP co. NP and NP co. NP Dp Polynomial hierarchy

What about? But how? Not clear on…Hmmm • Is problem A in NP? – Turing reductions – Many-one reductions • What about ~A (co. A)? – Reductions • But how to distinguish the differences? – In general, difference between NP and co. NP – Reductions, no clear distinction • Hmmm…. let’s classify co. NP

The Class co. NP • Class co. NP (Definition 7. 2) – Composed of the complements of problems in NP – The natural complement of NP problems • Same set of valid problem instances • “yes” and “no” NP problem answers reversed – Negation of the problem question • Conjecture – NP and co. NP are distinct

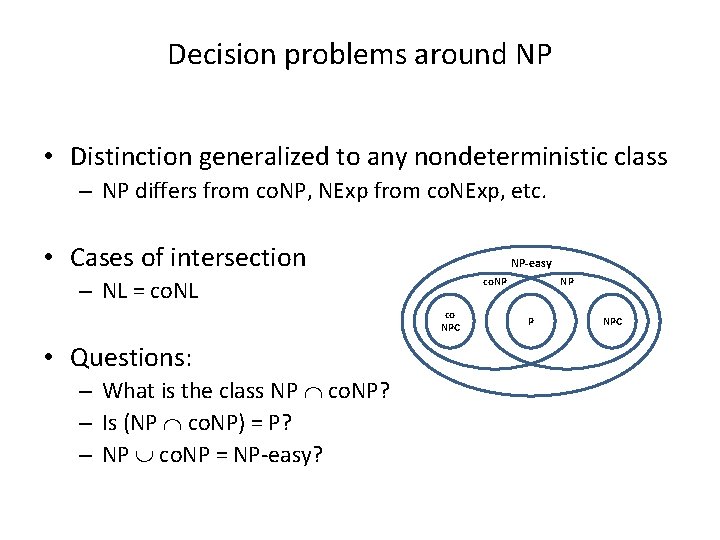
Decision problems around NP • Distinction generalized to any nondeterministic class – NP differs from co. NP, NExp from co. NExp, etc. • Cases of intersection NP-easy co. NP – NL = co. NL co NPC • Questions: – What is the class NP co. NP? – Is (NP co. NP) = P? – NP co. NP = NP-easy? NP P NPC

The NP co. NP class • What is NP co. NP? – problems in NP whose compliment is also in NP • Linear programming, primality testing • Is (NP co. NP) = P? – Not proven – Conjecture P (NP co. NP) • Duality of linear programs • Compositness and primality – Could indicate problem is in P

The Dp class • NP co. NP = NP-easy? – No – Dp • Class Dp (Definition 7. 3 p. 268) – Class of all sets Z that can be written as Z=X Y, for X NP and Y co. NP. • i. e. for any X in NP there is a problem Y in co. NP where the intersect of the two result in a “yes” instance. • Dp contains both NP and co. NP

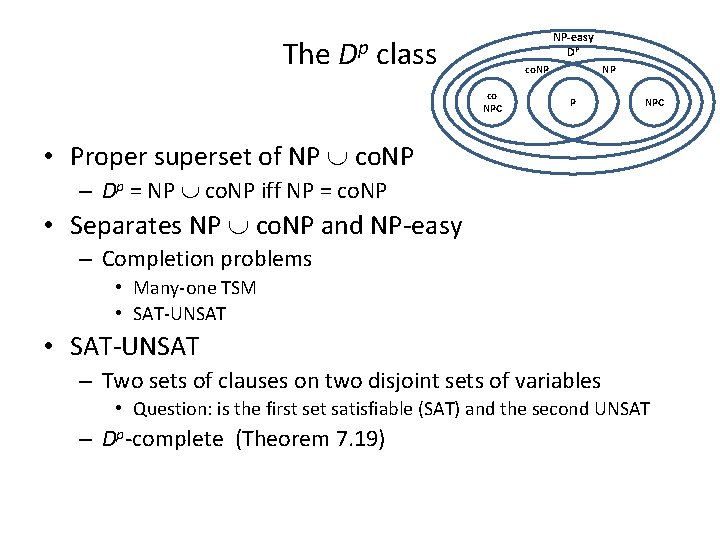
The Dp NP-easy DP class co. NP co NPC NP P NPC • Proper superset of NP co. NP – Dp = NP co. NP iff NP = co. NP • Separates NP co. NP and NP-easy – Completion problems • Many-one TSM • SAT-UNSAT – Two sets of clauses on two disjoint sets of variables • Question: is the first set satisfiable (SAT) and the second UNSAT – Dp-complete (Theorem 7. 19)

SAT-UNSAT is Dp-complete Proof • Prove that: – SAT-UNSAT is in Dp – Any problem in Dp reduces to it. • SAT-UNSAT is in Dp – Simply the intersection of SAT and UNSAT sets • SAT UNSAT • First set/half satisfiable? Yes • Second set/half unsatisfiable? Yes

SAT-UNSAT is Dp-complete Proof • Any problem in Dp reduces to it – Any problem X Dp can be written as X=Y 1 Y 2 • Problem of Y 1 NP and problem of Y 2 co. NP – SAT is NP-complete while UNSAT co. NP-complete • Y 1 ≤ SAT and Y 2 ≤ UNSAT • SAT ≤ SAT-UNSAT – Adding an UNSAT set of clauses of a different set of variables – Basically same for UNSAT ≤ SAT-UNSAT

SAT-UNSAT is Dp-complete Proof • Given and instance of X, x – x has an instance of Y 1 and Y 2 • Many-one reductions – Y 1 to SAT yields x 1 – Y 2 to UNSAT yields x 2 • The concatenation of yields a new instance of SATUNSAT – z = x 1 #x 2

Polynomial Hierarchy Do NP-easy problems constitute the set of all problems solvable in polynomial time if P equals NP? Any class with the property that collapses into P if P equals NP, exists as a separate entity only under assumption. Potentially infinite hierarchy of such classes is Polynomial hierarchy.

Polynomial Hierarchy Consider a class of NP easy decision problems. -- is a class of all decision problems solvable in polynomial time with the help of one oracle for some suitable NP-complete problem. -- all problems in NP are solvable by an oracle. Denoted by PNP.

Polynomial Hierarchy If P=NP, an oracle for NP would be oracle for P. We can always solve problems in polynomial time i. e. . , PNP = P. Assume P and NP differ and combine non-determinism, co-non-determinism and oracle mechanism and define further classes.

Polynomial Hierarchy Initially use a non deterministic polynomial time TM with oracle for NP. The resulting class would be NPNP. If P = NP then, NPNP = P

Polynomial Hierarchy Problems in NPNP were solvable in polynomial time, so would be problems in NP if and only if P = NP. Consider class containing complements of NPNP, co-NPNP and co-NPNP , both are one level higher in hierarchy. The hierarchies thus can extend to infinite levels.

Polynomial Hierarchy Definition: Is formed of three types of classes, each defined recursively: the deterministic classes, the non-deterministic classes and the co-non-deterministic classes which are recursively defined as follows

• Polynomial Hierarchy The Polynomial Hierarchy – One level

Polynomial Hierarchy If the hierarchy is infinite no complete problem can exist for PH itself. It is not known whether the hierarchy is truly infinite or collapses into some non deterministic class. We could have P =/= NP but NP = co. NP, where the whole hierarchy collapses to NP.

• Polynomial Hierarchy On the whole Polynomial Hierarchy explains the complexity of issues and surrounding the fundamental question of the relationship between P and NP.

7. 3. 3 ENUMERATION PROBLEMS

CONTENTS • Enumerations versions • #P class and significance • Completeness for #P - Using Parsimonious transformations • #P Complete related to NP and P • Comparison of #P complete problems

Enumeration vs Decision • Decision computes boolean valued function • Enumeration includes all integer valued functions • Presents number of Optimal or feasible solutions for given instance of problem • Defined for either decision, search or optimization problems • Enumeration leads to uncountable infinity of different solutions

• Enumeration versions are significantly harder - Hamiltonian circuits for a graph • Simple decision problems leads to harder enumeration -counting different spanning trees compared to finding single spanning tree • Some enumeration tasks can be solved in polynomial time -counting eulerian paths of graph -counting number of spanning trees

#P class • Def 7. 5 An integer-valued function f belongs to # p if there exists a deterministic Turing machine T and a polynomial p() such that , for each input string x, the value of the function f(x), is exactly equal to the number of distinct concise certificates for x. • NTM accepts x in exactly f(x) different ways • #P is the enumeration version of any problem in NP

• Set of counting problems associated with decision problems in set NP • NP is related with format “are there any” -Are there any subsets of a list of integers that add up to zero? -Are there any Hamiltonian cycles in a given graph with cost less than 100? (traveling salesman problem) • Corresponding #P asks “how many” -How many subsets of a list of integers add up to zero? -How many Hamiltonian cycles in a given graph have cost less than 100?

#P - Complete • Completeness of #P is defined based on polynomial reductions and transformations -What is the permanent of given matrix? -How many perfect matchings are there for a given bipartite graph? • Parsimonious defines the equality of solutions between original and transformed instance • Parsimonious transformation acts both reduction and transformation • Weakly parsimonious serves to prove #P completeness

• #P complete defines enumeration version of all NP-complete problems • Decision problems in P which are #P complete rises particular interest • Finding one perfect matching is solvable in polynomial time • Counting number of perfect matching in bipartite graph is #P complete

Comparing #P Complete • #P- complete problems are NP- hard • Solvability is based on the equality of P and NP • If P= NP , #P complete may remains intractable • #P-hardness acts as strong evidence of intractability • #P is difficult to compare with other complexity classes • #P-easy is used to compare

• Many counting problems in #P , hard don’t seem to #P complete • Counting the number of distinct isomorphism's between two graphs are NP-easy