The Poisson and Jump Processes Charles S Tapiero

The Poisson and Jump Processes Charles S. Tapiero

• Underlying the Poisson process are behavioral assumptions which are often justified in practice and used to characterize the mathematical representation of such processes. • There are two assumptions which lead to the Poisson process : • (1) Events are independent • (2) Events occur one at a time.

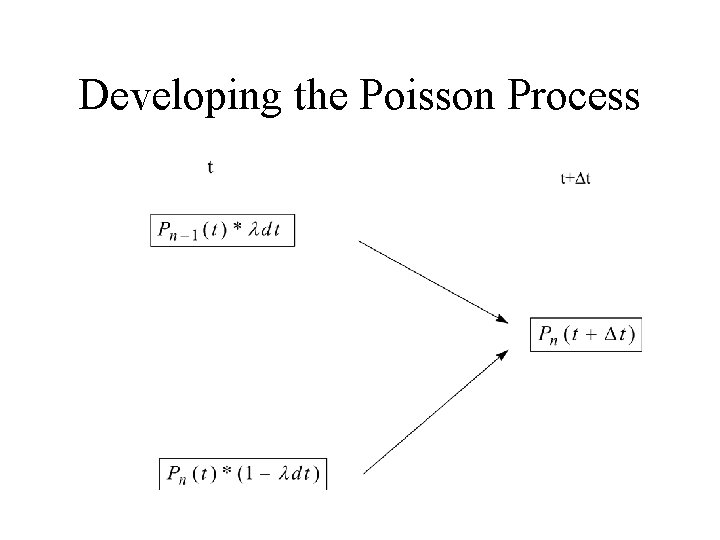
Developing the Poisson Process

The transition Probabilities

The solution

Verification

The Poisson process properties • independence • memory-less properties. • inter-event times are independently and identically distributed as exponential prob. distr. • This means that if we assume that the number of claims incoming to an insurance firm has a Poisson distribution, then this implies that the time between two consecutive claims are both independent and have an exponential probability distribution.

Mathematical Properties • The sums of Poisson generated events is also Poisson. • « fractionating » a Poisson process whose mean is m by a Bernoulli distribution with parameter p yields also a Poisson process with parameter mp.

Problem :

Collective risk and the compound Poisson process • In actuarial mathematics, a risk is a random variable on some probability space consisting of the claim size, and the number of claims. Thus, a risk is an independent sequence • where N is the number of claims (given by a Poisson distribution for example) and the claims which are assumed statistically independent. In this case, the risk defined by the total claims is given by : •

• Risk management consists in devising a number of rules which can reduce the risk. For example, if individual claims are limited to a maximal amount of a, then the risk is :

• while the complements may be insured by some reinsurer (who assumes this risk for a given premium which is negotiated between the first insurer and the reinsurer). • Credit unions are also, in some ways, similar to collective risk (mutual) insurance firms. They provide credit to consumers, particularly those with low incomes who are unable to pay the substantially higher fees and interest rates charged by banks.

• The mathematical analysis of such claim processes can be treated by the compound Poisson process. It is defined by

The study of processes is easily performed by using the probability generating function. For the Poisson distribution it is given by :

Thus, the probability generating function of the compound Poisson process is given by :

Using the formulas for mean and variance in terms of the probability generating function of random sums,

• Thus, if we were to consider again an insurance claim process where claim events occur at the Poisson rate • with a probability distribution for claim magnitudes given by • with mean and variance given by • then the mean and the expectation of claims and their variance over a period of time (0, t) are given by :

Note that if the claims process has a self participation clause of a and insurance covers all claims up to and including the amount b, the mean and the variance of the claim process are instead

Other and Generalized Jump Processes

Jump processes applications • Rare events • Imperfect markets price mechanims • ….