The PlanarReflective Symmetry Transform Princeton University Motivation Symmetry

The Planar-Reflective Symmetry Transform Princeton University

Motivation Symmetry is everywhere

Motivation Symmetry is everywhere Perfect Symmetry [Blum ’ 64, ’ 67] [Wolter ’ 85] [Minovic ’ 97] [Martinet ’ 05]

Motivation Symmetry is everywhere Local Symmetry [Blum ’ 78] [Mitra ’ 06] [Simari ’ 06]

Motivation Symmetry is everywhere Partial Symmetry [Zabrodsky ’ 95] [Kazhdan ’ 03]

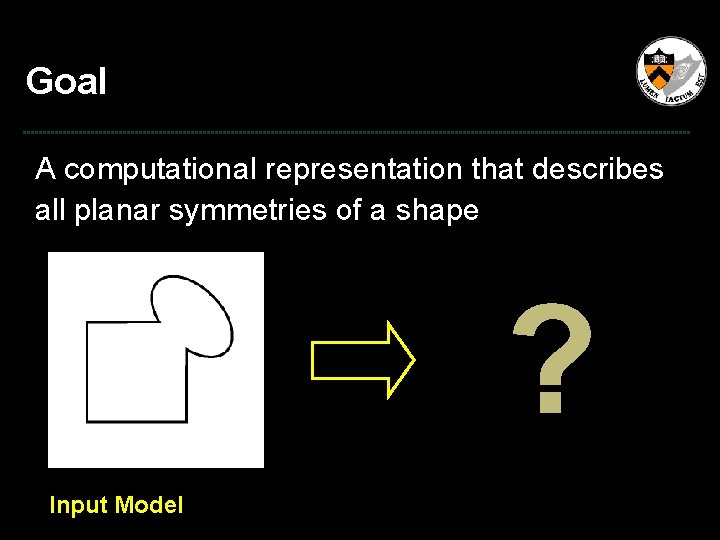
Goal A computational representation that describes all planar symmetries of a shape ? Input Model

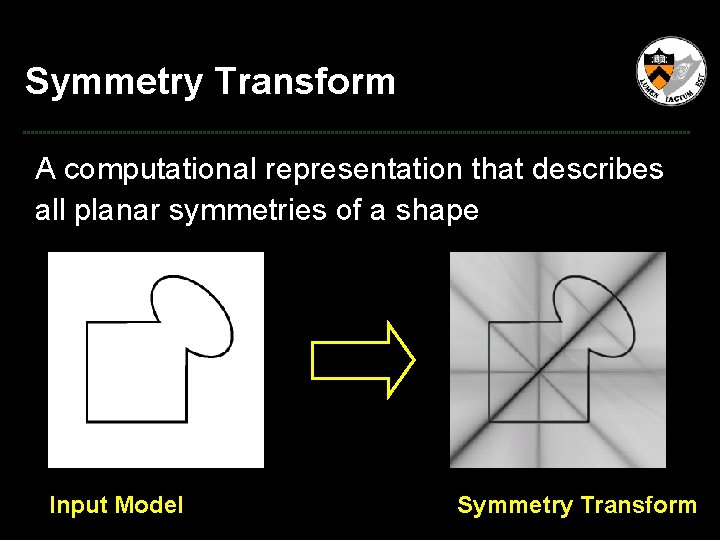
Symmetry Transform A computational representation that describes all planar symmetries of a shape ? Input Model Symmetry Transform

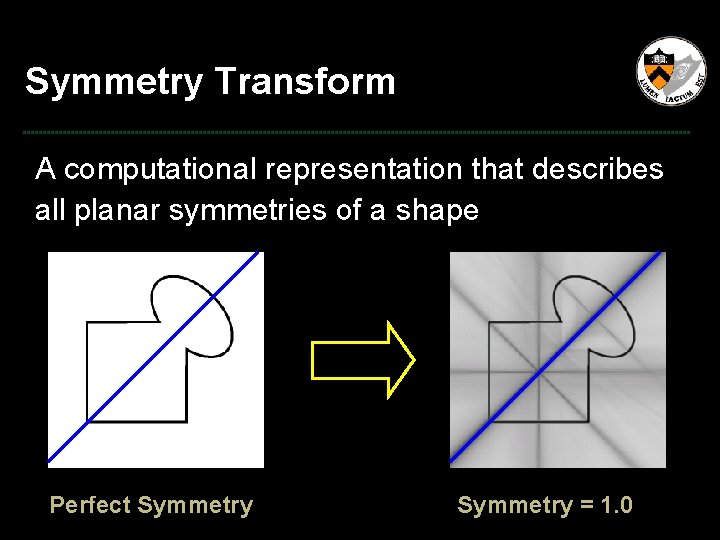
Symmetry Transform A computational representation that describes all planar symmetries of a shape ? Perfect Symmetry = 1. 0

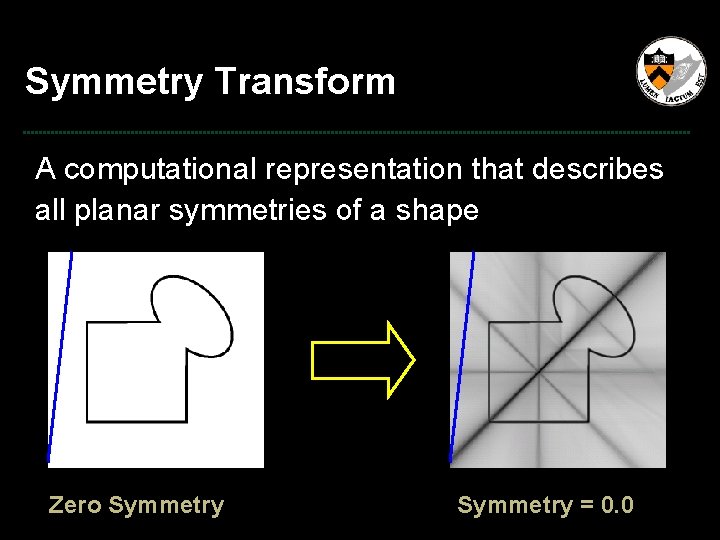
Symmetry Transform A computational representation that describes all planar symmetries of a shape ? Zero Symmetry = 0. 0

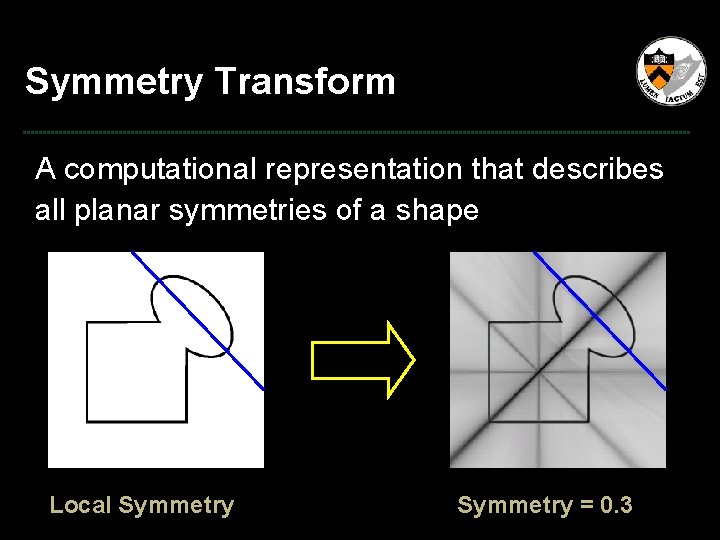
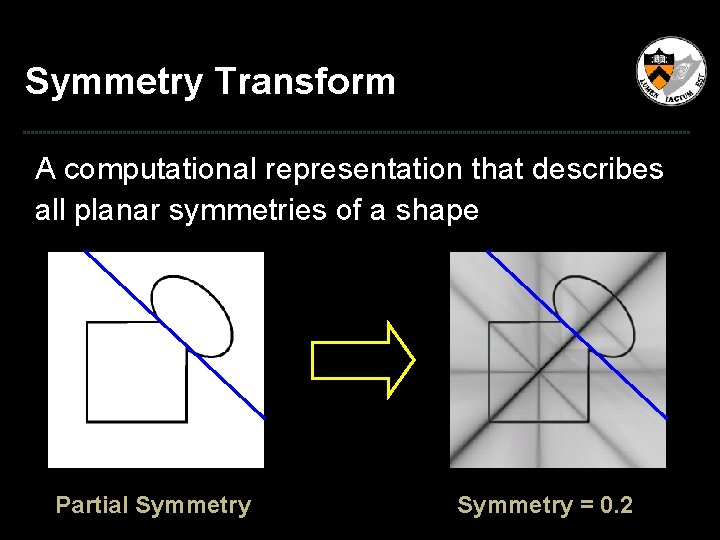
Symmetry Transform A computational representation that describes all planar symmetries of a shape ? Local Symmetry = 0. 3

Symmetry Transform A computational representation that describes all planar symmetries of a shape ? Partial Symmetry = 0. 2

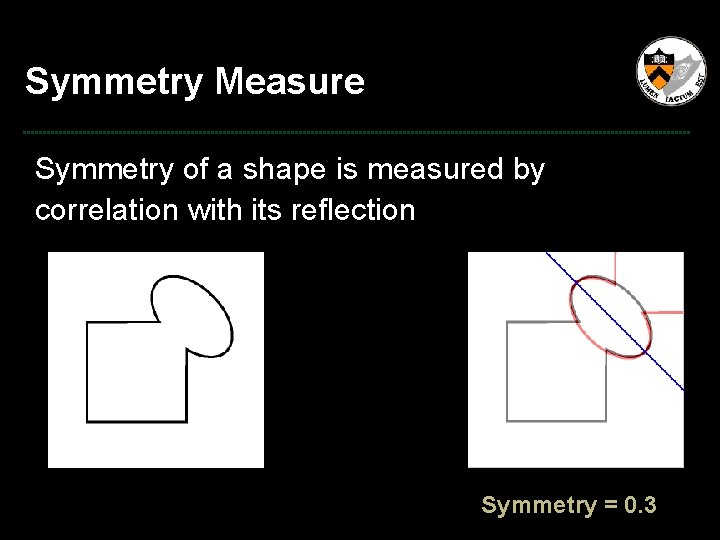
Symmetry Measure Symmetry of a shape is measured by correlation with its reflection

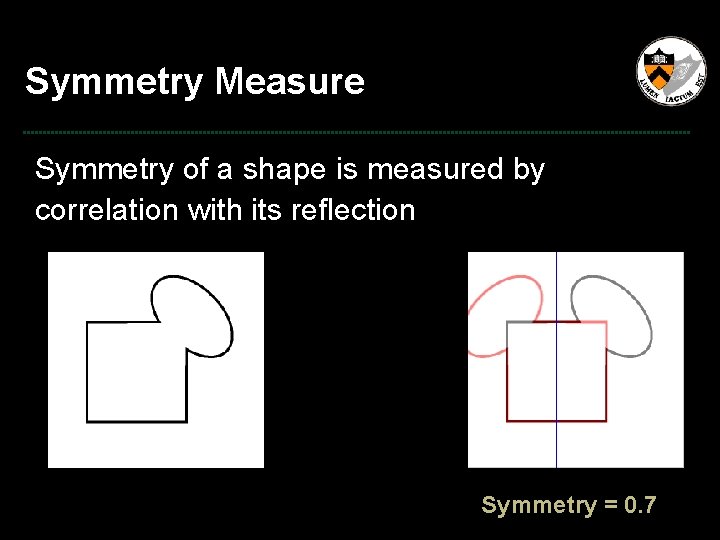
Symmetry Measure Symmetry of a shape is measured by correlation with its reflection Symmetry = 0. 7

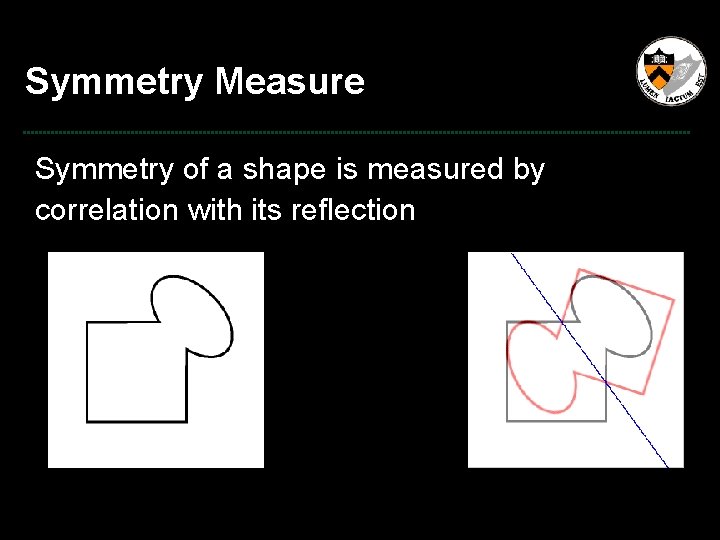
Symmetry Measure Symmetry of a shape is measured by correlation with its reflection Symmetry = 0. 3

Symmetry Measure Symmetry of a shape is measured by correlation with its reflection

Symmetry Measure Symmetry of a shape is measured by correlation with its reflection Symmetry = 0. 1

Outline • Introduction • Algorithm – Computing Discrete Transform – Finding Local Maxima Precisely • Applications – Alignment – Segmentation • Summary – Matching – Viewpoint Selection

Computing Discrete Transform n planes • Brute Force • Convolution • Monte-Carlo

Computing Discrete Transform O(n 3) planes X = O(n 6) O(n 3) dot product O(n 6) n planes • Brute Force • Convolution • Monte-Carlo

Computing Discrete Transform O(n 2) normal directions X = O(n 5 log n) O(n 3 log n) per direction O(n 6) O(n 5 Log n) n planes • Brute Force • Convolution • Monte-Carlo

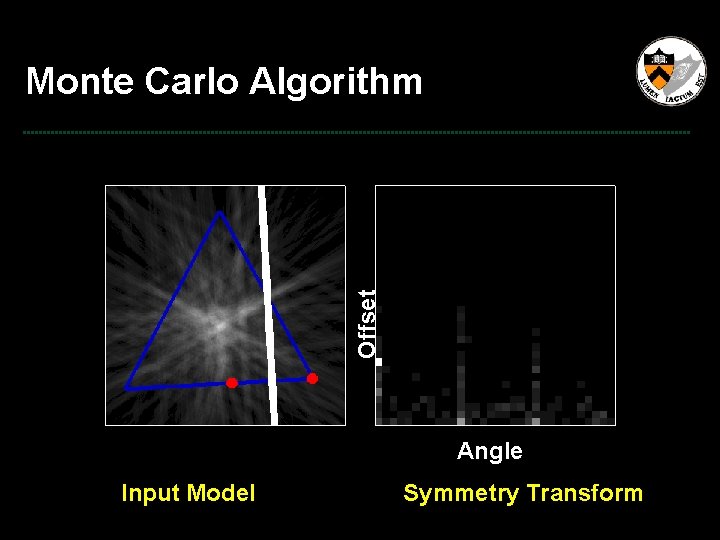
Computing Discrete Transform • Brute Force • Convolution • Monte-Carlo O(n 6) O(n 5 Log n) O(n 4) For 3 D meshes – Most of the dot product contains zeros. – Use Monte-Carlo Importance Sampling.

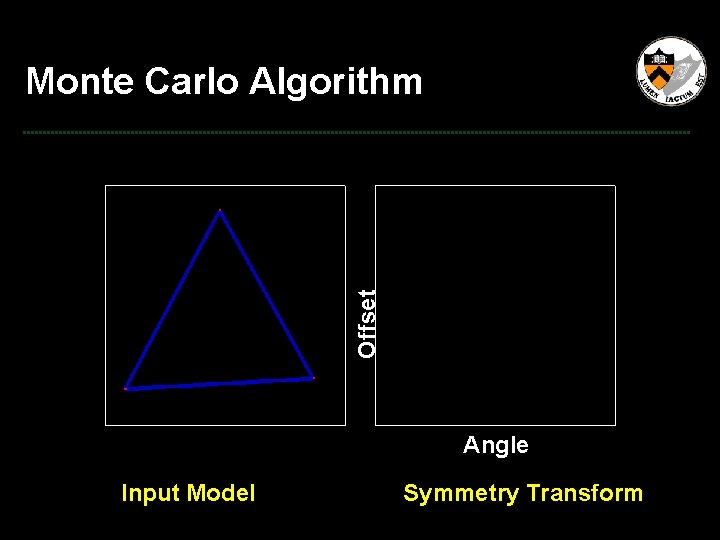
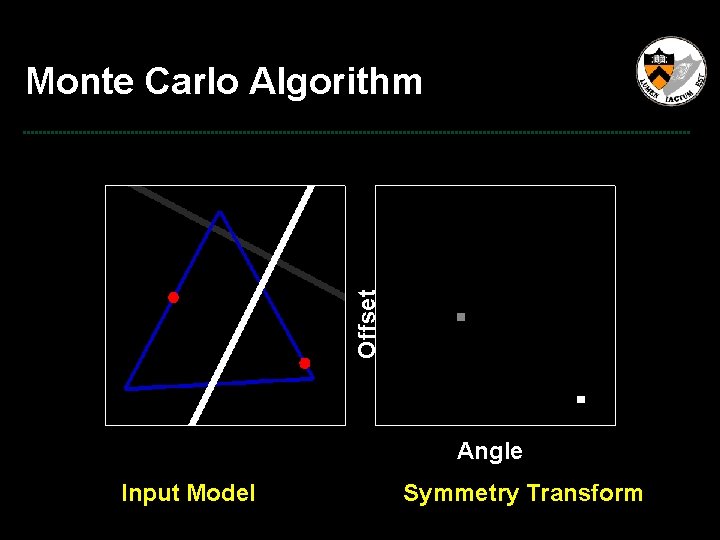
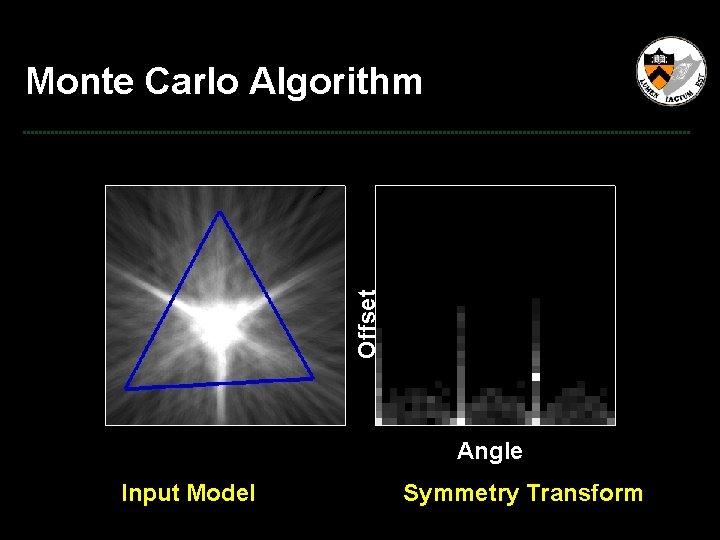
Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

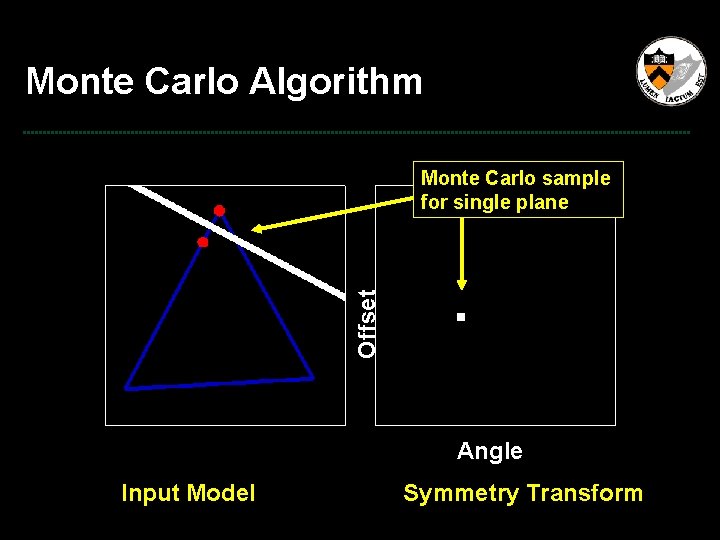
Monte Carlo Algorithm Offset Monte Carlo sample for single plane Angle Input Model Symmetry Transform

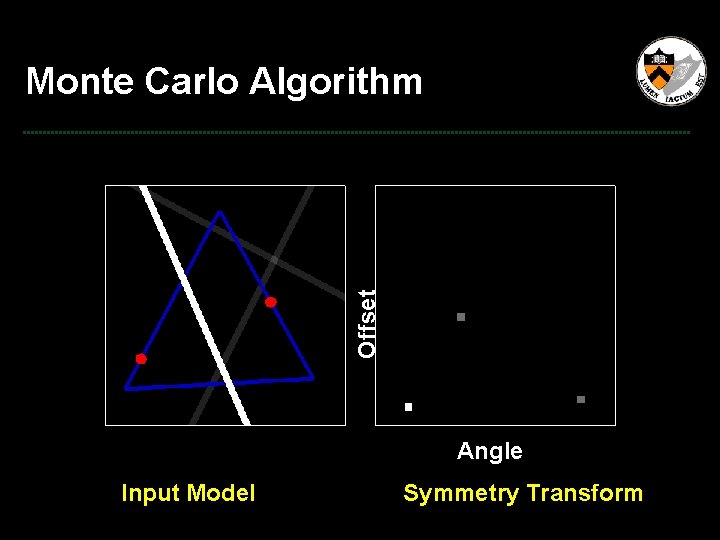
Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

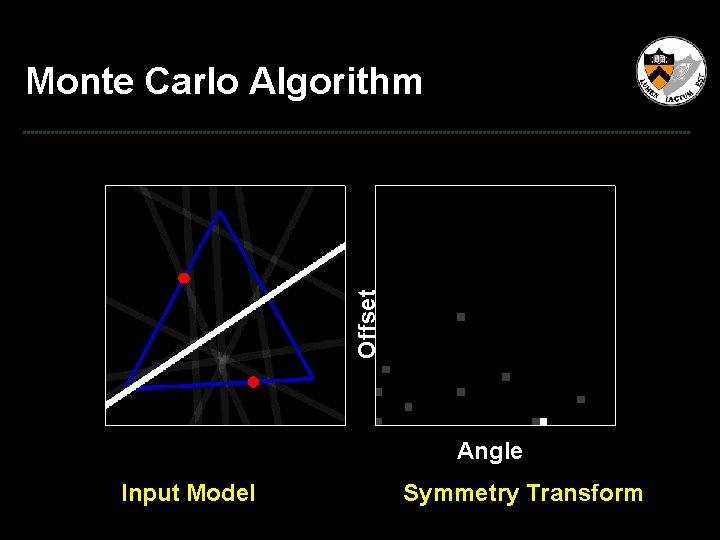
Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

Offset Monte Carlo Algorithm Angle Input Model Symmetry Transform

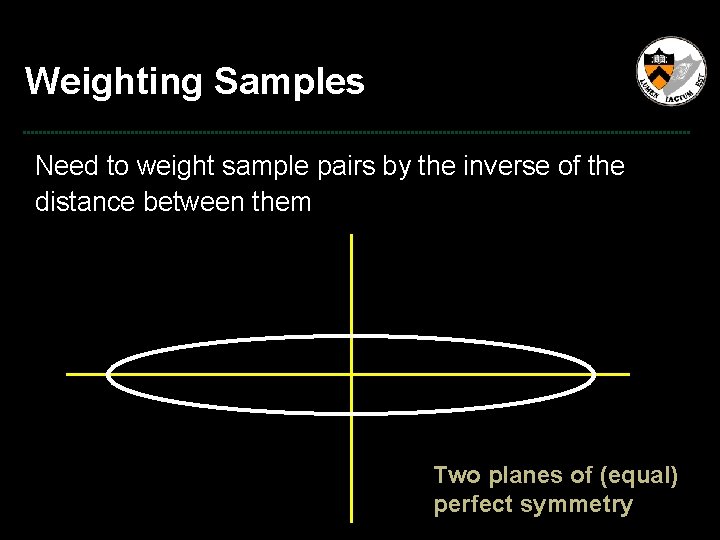
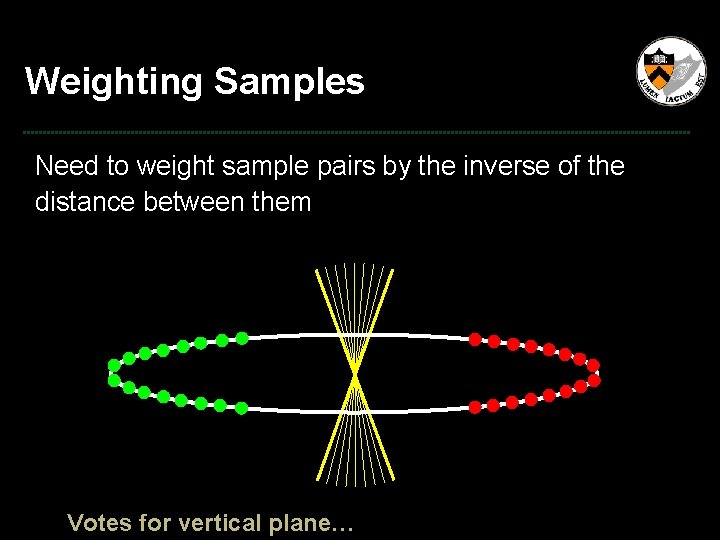
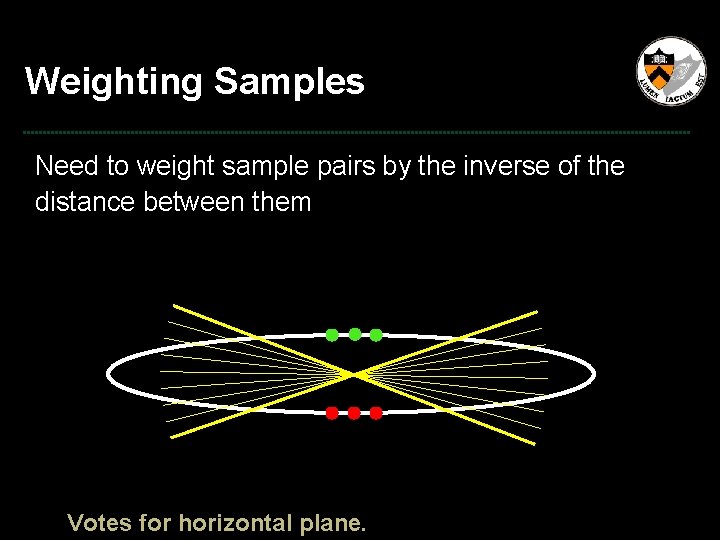
Weighting Samples Need to weight sample pairs by the inverse of the distance between them P 2 d P 1

Weighting Samples Need to weight sample pairs by the inverse of the distance between them Two planes of (equal) perfect symmetry

Weighting Samples Need to weight sample pairs by the inverse of the distance between them Votes for vertical plane…

Weighting Samples Need to weight sample pairs by the inverse of the distance between them Votes for horizontal plane.

Outline • Introduction • Algorithm – Computing Discrete Transform – Finding Local Maxima Precisely • Applications – Alignment – Segmentation • Summary – Matching – Viewpoint Selection

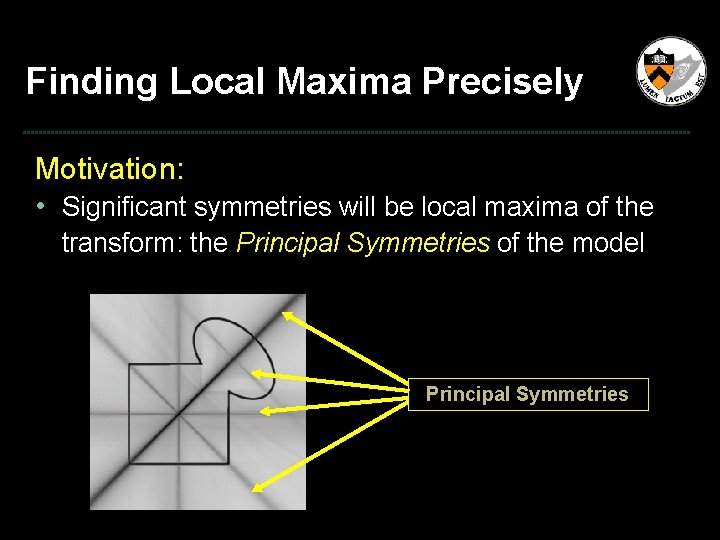
Finding Local Maxima Precisely Motivation: • Significant symmetries will be local maxima of the transform: the Principal Symmetries of the model Principal Symmetries

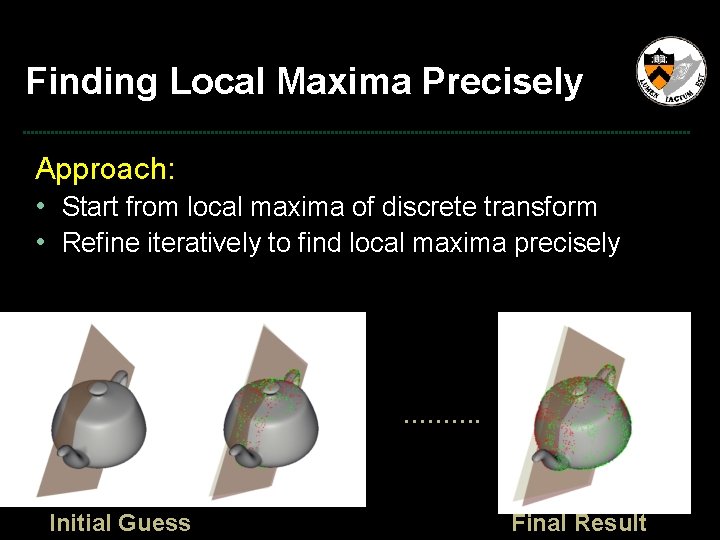
Finding Local Maxima Precisely Approach: • Start from local maxima of discrete transform

Finding Local Maxima Precisely Approach: • Start from local maxima of discrete transform • Refine iteratively to find local maxima precisely ………. Initial Guess Final Result

Outline • Introduction • Algorithm – Computing discrete transform – Finding Local Maxima Precisely • Applications – Alignment – Segmentation • Summary – Matching – Viewpoint Selection

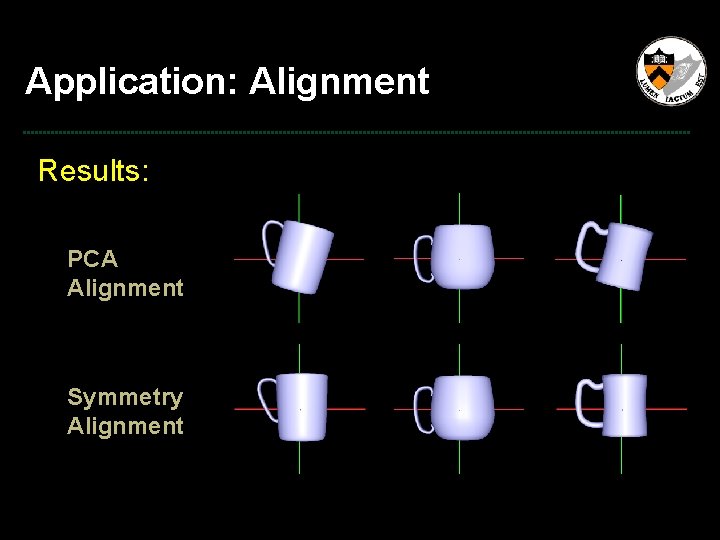
Application: Alignment Motivation: • Composition of range scans • Feature mapping PCA Alignment

Application: Alignment Approach: • Perpendicular planes with the greatest symmetries create a symmetry-based coordinate system.

Application: Alignment Approach: • Perpendicular planes with the greatest symmetries create a symmetry-based coordinate system.

Application: Alignment Approach: • Perpendicular planes with the greatest symmetries create a symmetry-based coordinate system.

Application: Alignment Approach: • Perpendicular planes with the greatest symmetries create a symmetry-based coordinate system.

Application: Alignment Results: PCA Alignment Symmetry Alignment

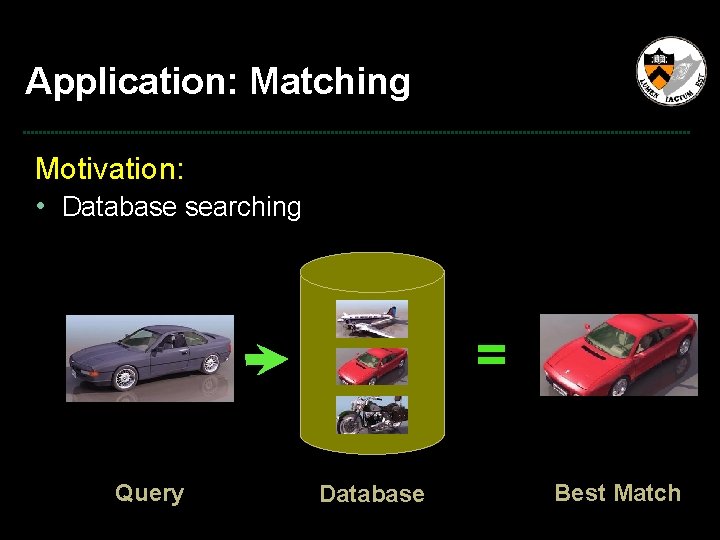
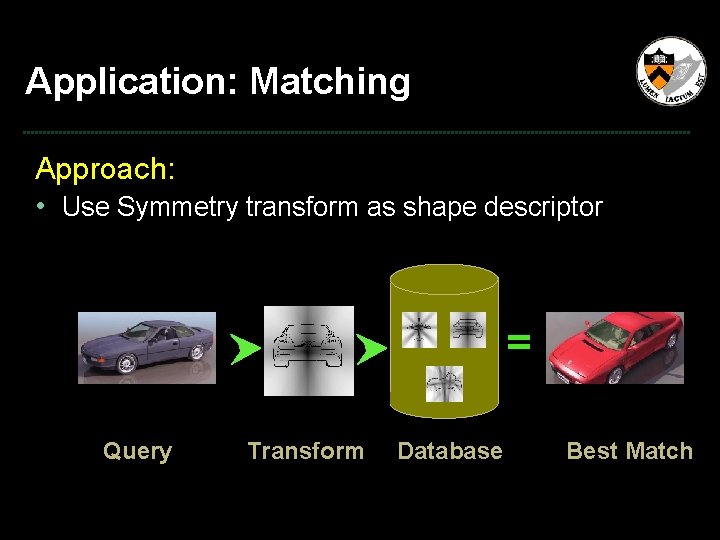
Application: Matching Motivation: • Database searching = Query Database Best Match

Application: Matching Observation: • All chairs display similar principal symmetries

Application: Matching Approach: • Use Symmetry transform as shape descriptor = Query Transform Database Best Match

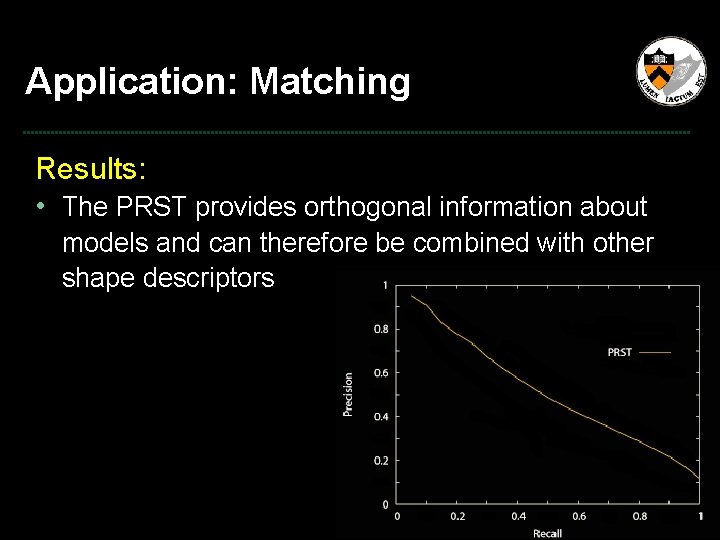
Application: Matching Results: • The PRST provides orthogonal information about models and can therefore be combined with other shape descriptors

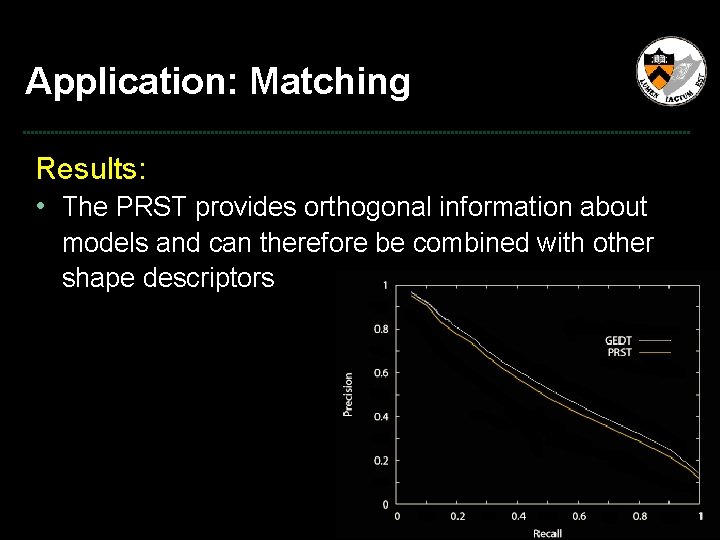
Application: Matching Results: • The PRST provides orthogonal information about models and can therefore be combined with other shape descriptors

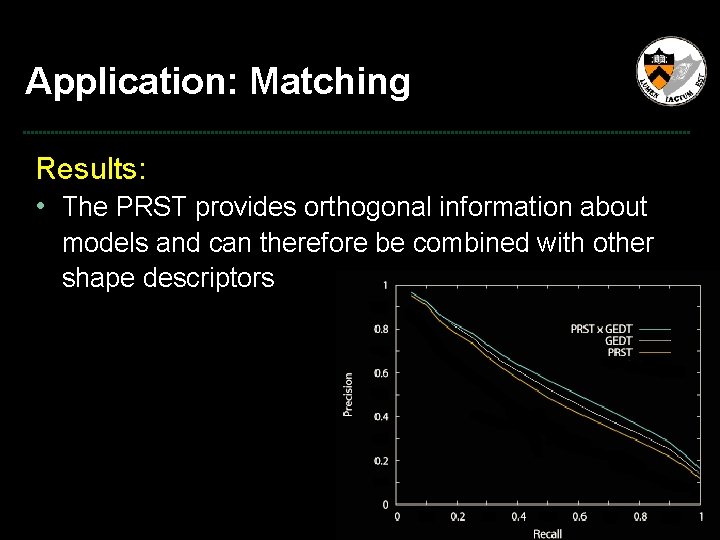
Application: Matching Results: • The PRST provides orthogonal information about models and can therefore be combined with other shape descriptors

Application: Segmentation Motivation: • Modeling by parts • Collision detection [Chazelle ’ 95][Li ’ 01] [Mangan ’ 99][Garland ’ 01] [Katz ’ 03]

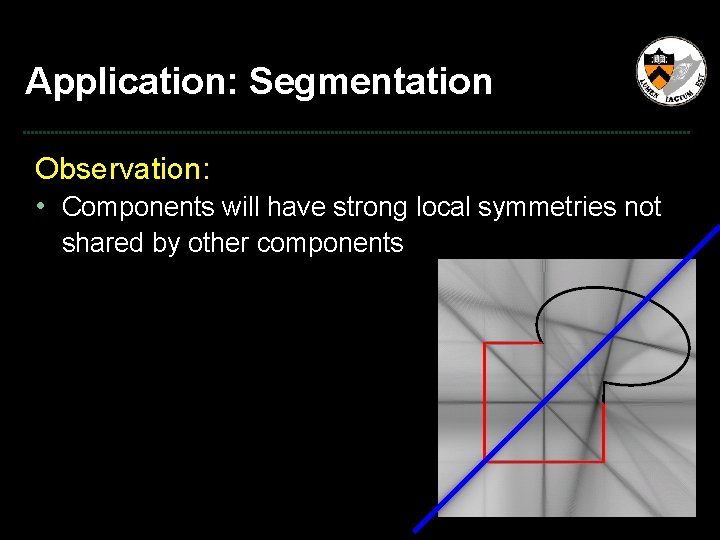
Application: Segmentation Observation: • Components will have strong local symmetries not shared by other components

Application: Segmentation Observation: • Components will have strong local symmetries not shared by other components

Application: Segmentation Observation: • Components will have strong local symmetries not shared by other components

Application: Segmentation Observation: • Components will have strong local symmetries not shared by other components

Application: Segmentation Observation: • Components will have strong local symmetries not shared by other components

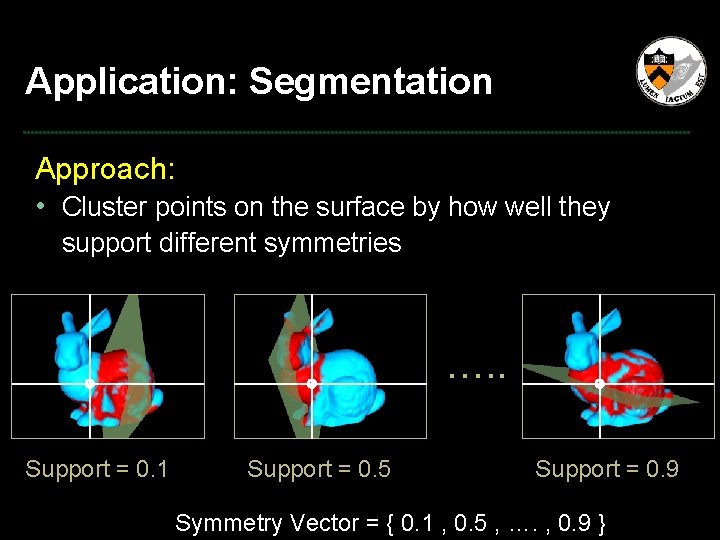
Application: Segmentation Approach: • Cluster points on the surface by how well they support different symmetries …. . Support = 0. 1 Support = 0. 5 Support = 0. 9 Symmetry Vector = { 0. 1 , 0. 5 , …. , 0. 9 }

Application: Segmentation Results:

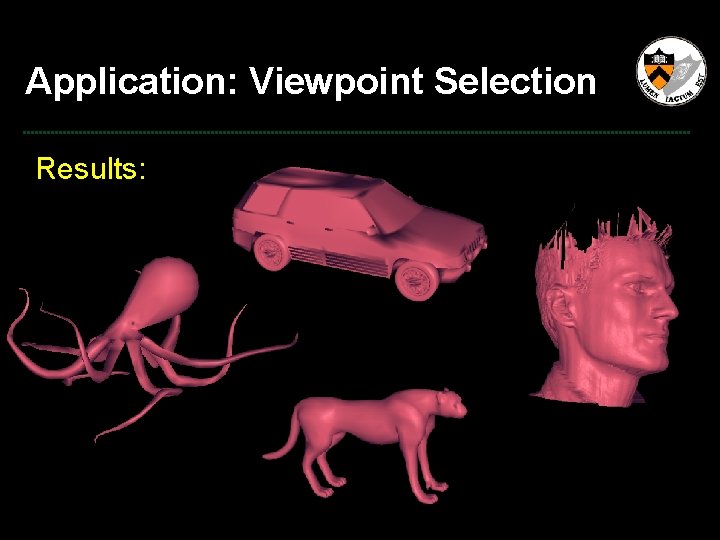
Application: Viewpoint Selection Motivation: • Catalog generation • Image Based Rendering [Blanz ’ 99][Vasquez ’ 01] [Lee ’ 05][Abbasi ’ 00] Picture from Blanz et al. ‘ 99

Application: Viewpoint Selection Approach: • Symmetry represents redundancy in information.

Application: Viewpoint Selection Approach: • Symmetry represents redundancy in information • Minimize the amount of visible symmetry • Every plane of symmetry votes for a viewing direction perpendicular to it Best Viewing Directions

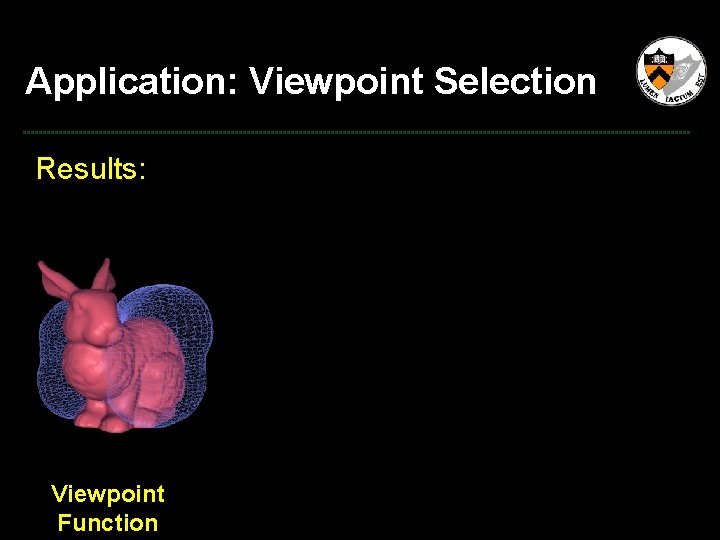
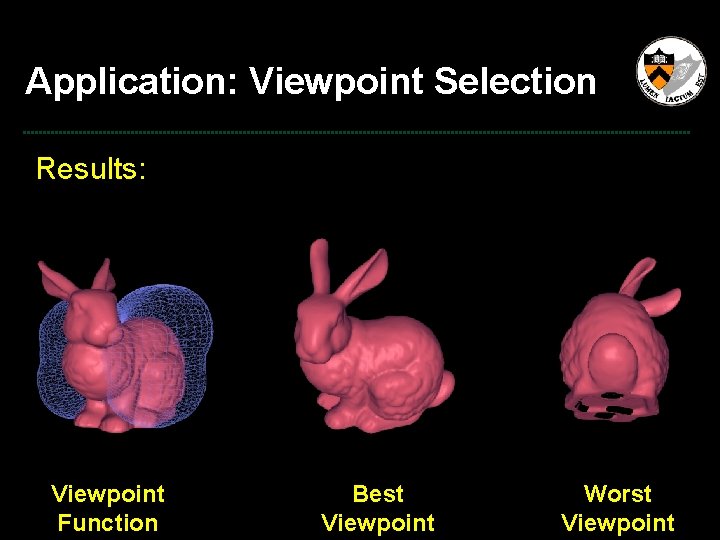
Application: Viewpoint Selection Results: Viewpoint Function

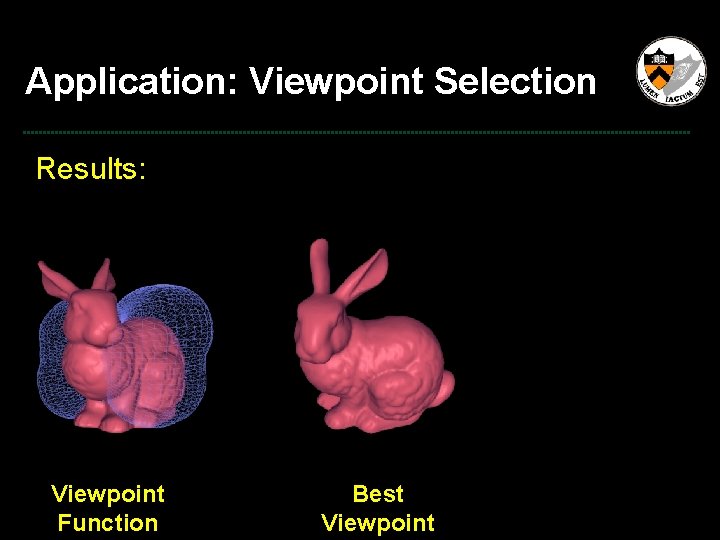
Application: Viewpoint Selection Results: Viewpoint Function Best Viewpoint

Application: Viewpoint Selection Results: Viewpoint Function Best Viewpoint Worst Viewpoint

Application: Viewpoint Selection Results:

Summary • Symmetry Transform – Symmetry measure for all planes in space • Algorithms – Discrete set of planes – Finding local maxima precisely • Applications – Alignment – Matching – Segmentation – Viewpoint Selection

Future Work Extended forms of symmetry • Rotational symmetry • Point symmetry • General transform symmetry Signal processing Further applications • Compression • Constrained editing • Etc.

Acknowledgements: Princeton Graphics • Chris De. Coro • Michael Kazhdan Funding • Air Force Research Lab grant #FA 8650 -04 -1 -1718 • NSF grant #CCF-0347427 • NSF grant #CCR-0093343 • NSF grant #IIS-0121446 • The Sloan Foundation

The End

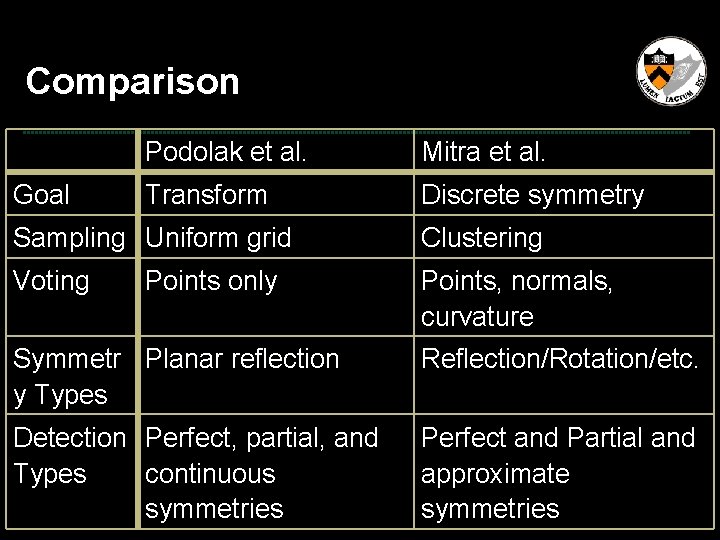
Comparison Goal Podolak et al. Mitra et al. Transform Discrete symmetry Sampling Uniform grid Clustering Voting Points, normals, curvature Points only Symmetr Planar reflection y Types Reflection/Rotation/etc. Detection Perfect, partial, and Types continuous symmetries Perfect and Partial and approximate symmetries