The Physics of Synchrotron Radiation Sources An Introduction

The Physics of Synchrotron Radiation Sources: An Introduction Pedro F. Tavares MAX IV Laboratory Lund, Sweden Nathiagali Summer College, June 2013 38 th Nathiagali Summer School

The Physics of Synchrotron Radiation Sources: An Introduction Prerequisites: Classical electromagnetism, Relativistic mechanics, a bit of quantum mechanics. No specific knowledge of accelerators is assumed. Objectives Review the fundamentals of Synchrotron Light Sources. Highlight recent trends in Light Source Design and Development. Focus on SR based sources. Illustrate how diverse and exciting are the challenges faced by today’s light source designers. June 2013 38 th Nathiagali Summer School

The Physics of Synchrotron Radiation Sources: An Introduction References H. Wiedemann, Particle Accelerator Physics I and II, Springer Verlag. M. Sands, The Physics of Electron Storage Rings D. A. Edwards and M. J. Syphers, An Introduction to the Physics of High Energy Accelerators, Wiley CAS – CERN Accelerator Schools (Basic and Advanced) USPAS – US Particle Accelerator School June 2013 38 th Nathiagali Summer School

The Physics of Synchrotron Radiation Sources: An Introduction Lecture #1 – Synchrotron Radiation and its Properties. Why do it ? Lecture #2 – The Physics of Electron Storage Rings. How to do it ? Lecture #3 – Recent Trends in Storage Ring Based Source Design: The MAX IV Project. A new wave of light sources. June 2013 38 th Nathiagali Summer School

Lecture #1: Properties of Synchrotron Radiation What is Synchrotron Radiation ? Why Synchrotron Radiation ? Synchrotron Radiation Sources and their properties. Bending Magnet Radiation: the basics. Insertion Device Radiation: incoherent sum vs coherent superposition. Light Source Figures of Merit: comparing light sources. Coherent Synchrotron Radiation Sources: when 1+1 is 4 ! Other Types of Light Sources: Free Electron Lasers : making instabilities work for you. Energy Recovery Linacs: the best of two worlds June 2013 38 th Nathiagali Summer School

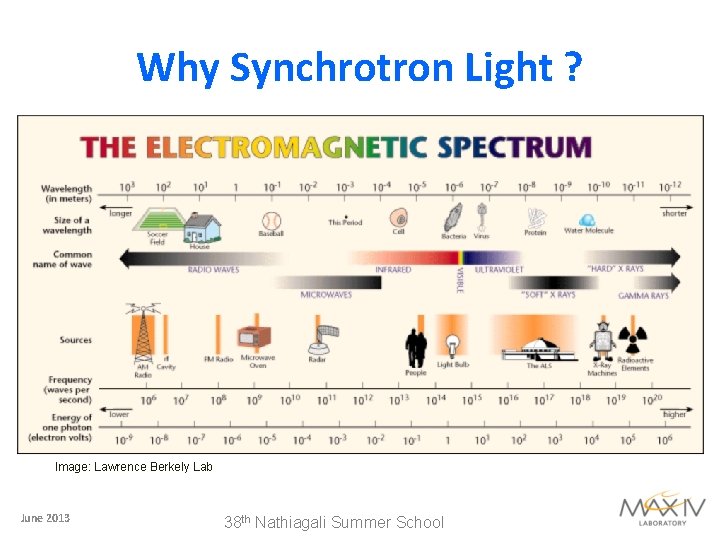
What is Synchrotron Radiation? EM radiation from accelerated charged particles Properties: Wide band High intensity/Brilliance www. lightsources. org June 2013 Polarization 38 th Nathiagali Summer School Time structure

Using Light To Understand the World Anton van Leeuwenhoek 1632 -1723 Galileo 1564 - 1642 The telescope is presented to the Doge of Venice June 2013 38 th Nathiagali Summer School

Why Synchrotron Light ? Image: Lawrence Berkely Lab June 2013 38 th Nathiagali Summer School

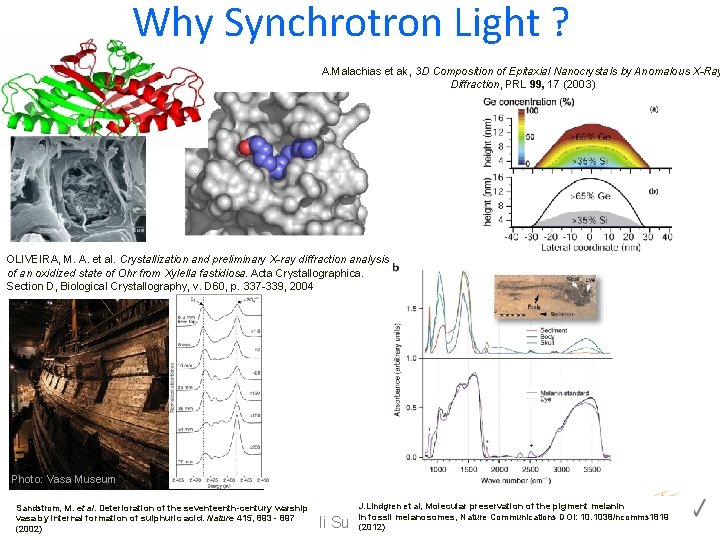
Why Synchrotron Light ? A. Malachias et ak, 3 D Composition of Epitaxial Nanocrystals by Anomalous X-Ray Diffraction, PRL 99, 17 (2003) OLIVEIRA, M. A. et al. Crystallization and preliminary X-ray diffraction analysis of an oxidized state of Ohr from Xylella fastidiosa. Acta Crystallographica. Section D, Biological Crystallography, v. D 60, p. 337 -339, 2004 Photo: Vasa Museum Sandstrom, M. et al. Deterioration of the seventeenth-century warship vasa internal formation of sulphuric acid. Nature 415, Juneby 2013 th 893 - 897 (2002) J. Lindgren et al, Molecular preservation of the pigment melanin in fossil melanosomes, Nature Communications DOI: 10. 1038/ncomms 1819 (2012) 38 Nathiagali Summer School

June 2013 38 th Nathiagali Summer School

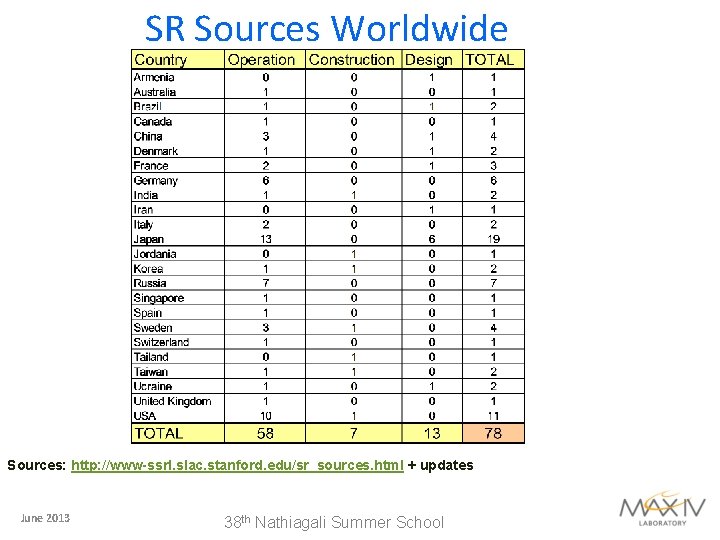
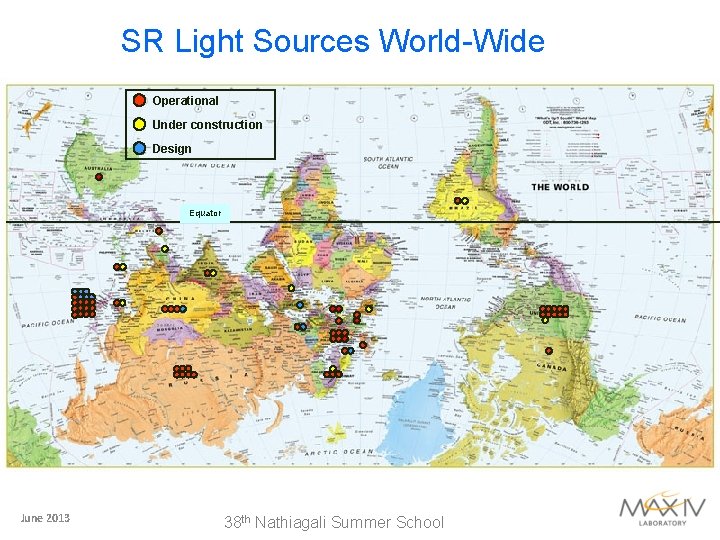
SR Sources Worldwide Sources: http: //www-ssrl. slac. stanford. edu/sr_sources. html + updates June 2013 38 th Nathiagali Summer School

SR Light Sources World-Wide Operational Under construction Design Equator June 2013 38 th Nathiagali Summer School

SR in nature too ! Jupiter Crab Nebula Image: Imke de Pater June 2013 38 th Nathiagali Summer School From hyperphysics. phy-astr. gsu. edu

The Larmor Formula E. M. Purcell, Electricity and Magnetism June 2013 38 th Nathiagali Summer School

E. M. Emission from Accelerated Charged Particles Basic Properties June 2013 38 th Nathiagali Summer School

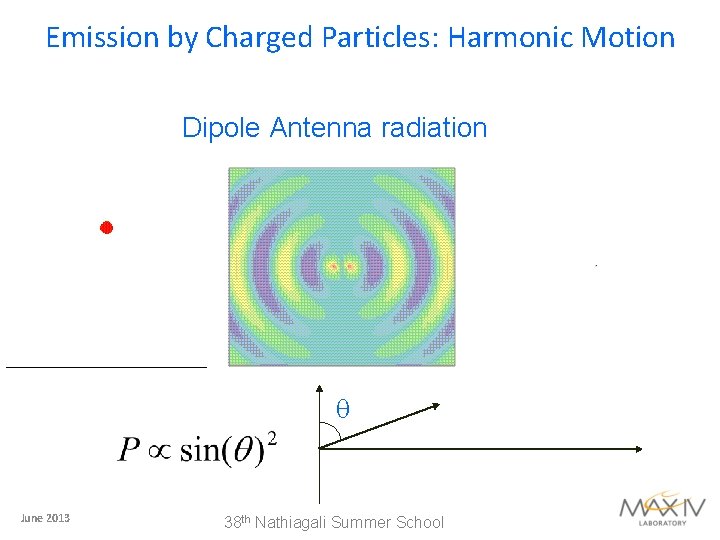
Emission by Charged Particles: Harmonic Motion Dipole Antenna radiation q June 2013 38 th Nathiagali Summer School

Emission by particle in circular motion v<<c June 2013 38 th Nathiagali Summer School v=0. 7 c

Angular Distribution Acceleration perpendicular to velocity Pic from H. Wiedemann Non-relativistic Ultra-relativistic For E=3 Ge. V June 2013 38 th Nathiagali Summer School

Total Power Transverse Longitudinal For relativistic velocities: Fixed radius/momentum: June 2013 38 th Nathiagali Summer School Electrons>>protons

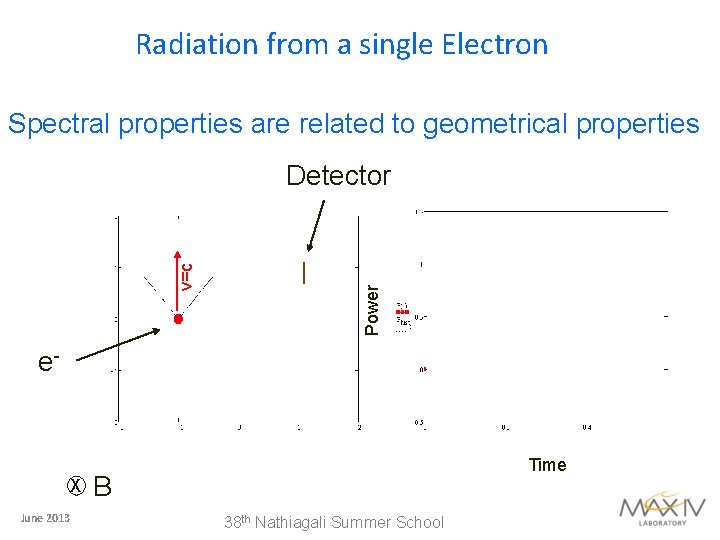
Radiation from a single Electron Spectral properties are related to geometrical properties Power v=c Detector e- X June 2013 Time B 38 th Nathiagali Summer School

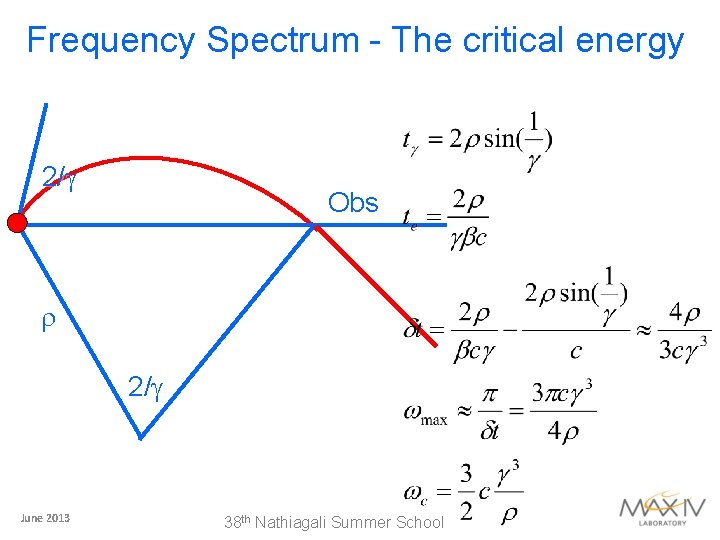
Frequency Spectrum - The critical energy 2/g Obs r 2/g June 2013 38 th Nathiagali Summer School

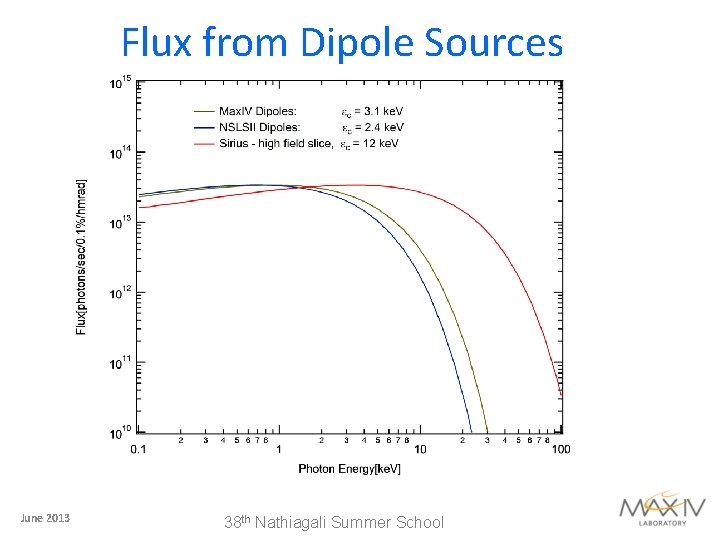
Flux from Dipole Sources June 2013 38 th Nathiagali Summer School

Insertion Devices Undulator Periodic arrays of magnets cause the beam to “undulate” Photo E. Wallen Wiggler www. lightsources. org June 2013 38 th Nathiagali Summer School

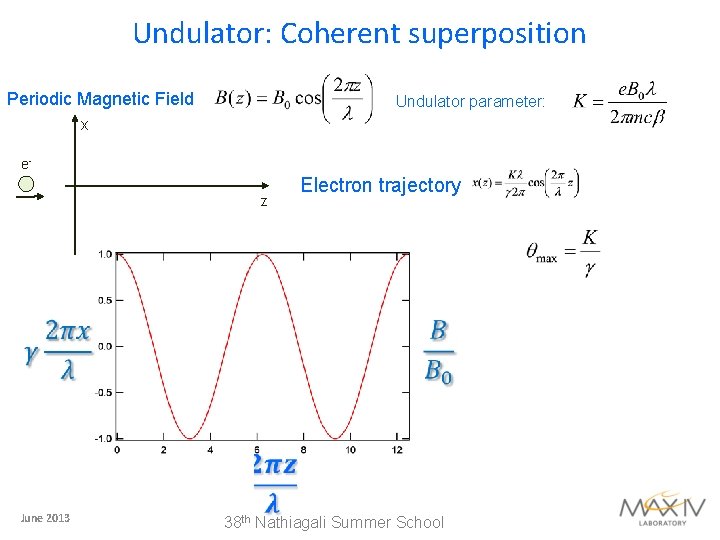
Undulator: Coherent superposition Periodic Magnetic Field Undulator parameter: x ez June 2013 Electron trajectory 38 th Nathiagali Summer School

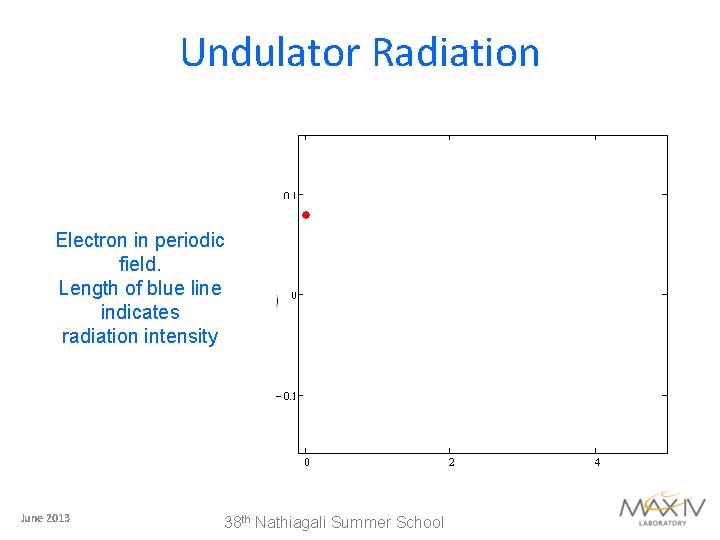
Undulator Radiation Electron in periodic field. Length of blue line indicates radiation intensity June 2013 38 th Nathiagali Summer School

Undulator Radiation Detector Power Photons emitted at each pole Time domain signal is a periodic sequence of pulses – in the frequency domain: emission at a fundamental frequency. June 2013 38 th Nathiagali Summer School

Undulator Radiation trajectory Electron path length Photon Path length slope Electron time Time Difference Undulator Fundamental June 2013 38 th Nathiagali Summer School Photon time

Undulator Radiation Alternative views: Electromagnetic waves emitted from different periods interfere constructively at chosen wavelengths • For K<<1, motion in a frame moving along with the average longitudinal electron velocity is harmonic. • A single frequency is generated. • Period is Lorentz contracted in moving frame. Radiation frequency is doppler shifted in the lab frame. • As K increases : the transverse motion is perturbed harmonics of the fundamental frequency show up. (Since the perturbation is symmetric only ODD harmonics appear in the forward direction). Coherent superposition is only possible if the angular aperture of the radiation is much larger than maximum orbit angular deviation. H. Wiedemann, Part. Acc. Physics, Vol I June 2013 38 th Nathiagali Summer School

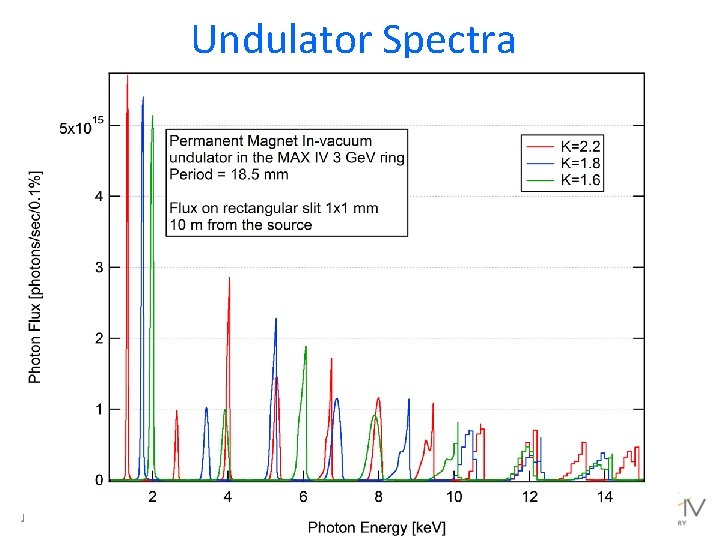
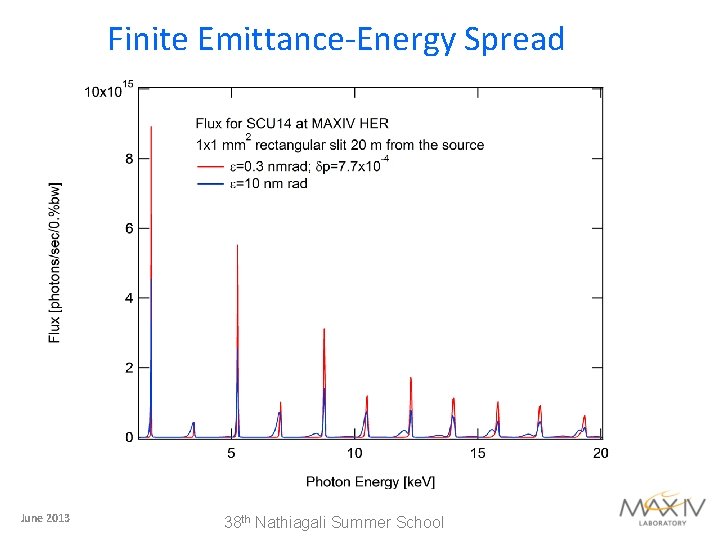
Undulator Spectra For a single electron: In a real beam, this deteriorates due to the finite spatial and angular extent (emittance) and energy spread June 2013 38 th Nathiagali Summer School

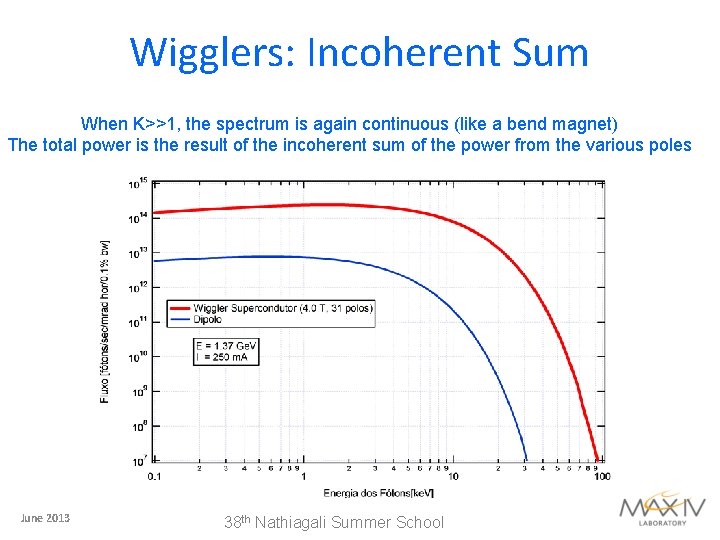
Wigglers: Incoherent Sum When K>>1, the spectrum is again continuous (like a bend magnet) The total power is the result of the incoherent sum of the power from the various poles June 2013 38 th Nathiagali Summer School

Engineering compromises in ID Design Hybrid PM device June 2013 38 th Nathiagali Summer School

June 2013 38 th Nathiagali Summer School

Light Source Figures of Merit Intensity and spectral range Time structure Brilliance/Brightness Flux density Average vs Peak Values Polarization Coherence Stability June 2013 38 th Nathiagali Summer School

Spectral Brightness Photon Phase Space Density in photon phase space In an ideal optical transport system, brightness is conserved – a property of the source. Several derived quantities are often used Central Brightness Angular density of flux H. Wiedemann, Part. Acc. Phys, Vol II June 2013 38 th Nathiagali Summer School

Brightness from a real beam Convolute the angular distribution of radiation from a single electron with the electron beam transverse spatial and angular distributions For the n-th harmonic of an undulator of length L Spectral flux (E, I, B, n) Electron beam Effective source size and divergence Diffraction Limit: June 2013 e-beam emittance 38 th Nathiagali Summer School

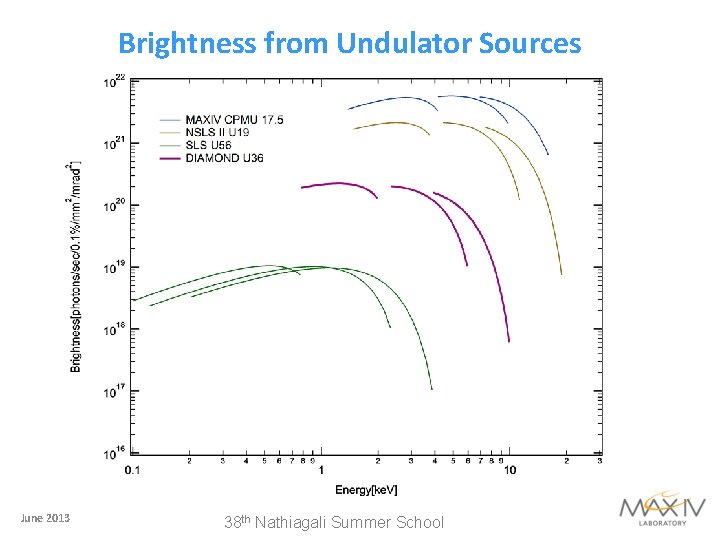
Brightness from Undulator Sources June 2013 38 th Nathiagali Summer School

Finite Emittance-Energy Spread June 2013 38 th Nathiagali Summer School

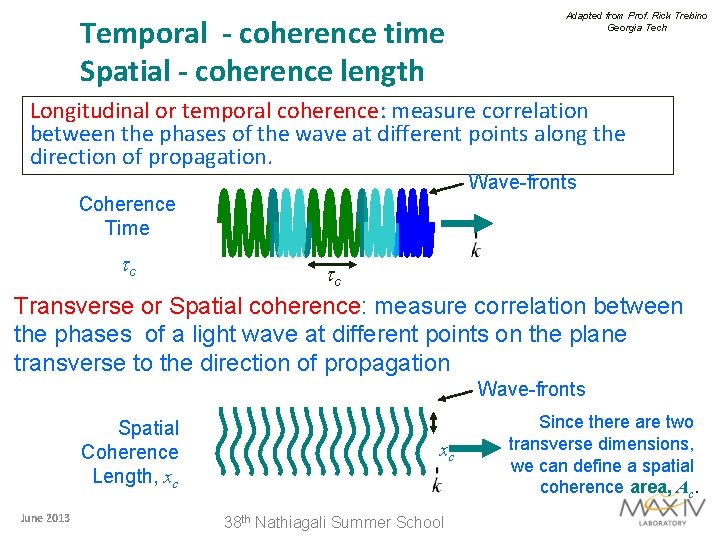
Temporal - coherence time Spatial - coherence length Adapted from Prof. Rick Trebino Georgia Tech Longitudinal or temporal coherence: measure correlation between the phases of the wave at different points along the direction of propagation. Wave-fronts Coherence Time tc tc Transverse or Spatial coherence: measure correlation between the phases of a light wave at different points on the plane transverse to the direction of propagation Wave-fronts Spatial Coherence Length, xc June 2013 xc 38 th Nathiagali Summer School Since there are two transverse dimensions, we can define a spatial coherence area, Ac.

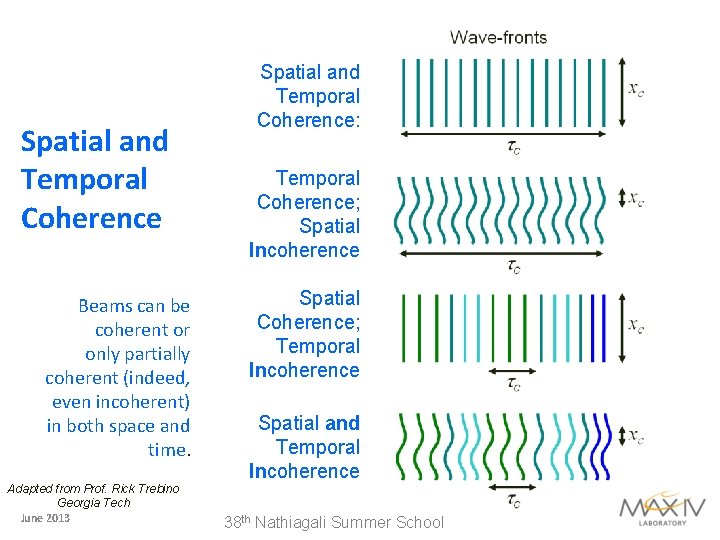
Spatial and Temporal Coherence Beams can be coherent or only partially coherent (indeed, even incoherent) in both space and time. Adapted from Prof. Rick Trebino Georgia Tech June 2013 Spatial and Temporal Coherence: Temporal Coherence; Spatial Incoherence Spatial Coherence; Temporal Incoherence Spatial and Temporal Incoherence 38 th Nathiagali Summer School

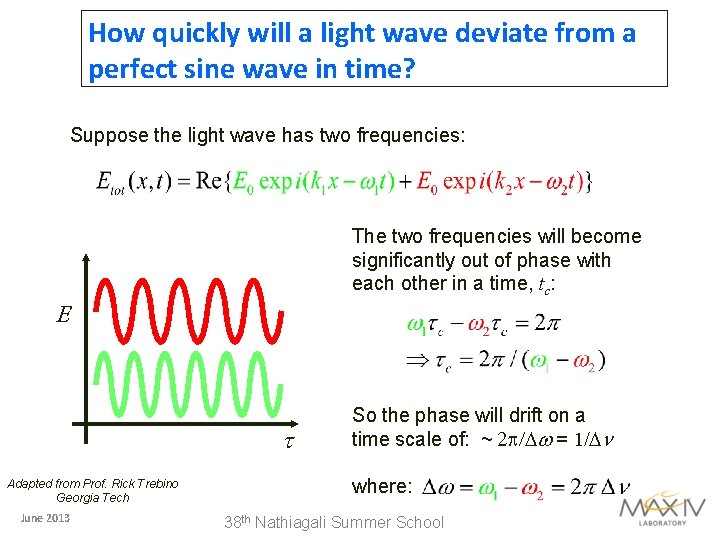
How quickly will a light wave deviate from a perfect sine wave in time? Suppose the light wave has two frequencies: The two frequencies will become significantly out of phase with each other in a time, tc: E t Adapted from Prof. Rick Trebino Georgia Tech June 2013 So the phase will drift on a time scale of: ~ 2 p/Dw = 1/Dn where: 38 th Nathiagali Summer School

Transverse Coherence and Brightness Coherence of electromagnetic perturbations at two points on a plane perpendicular to the direction of propagation. Relates to the capability to generate interference patterns Maximum Brightness (diffraction limited source): Coherent Flux: Harder for short wavelengths June 2013 38 th Nathiagali Summer School

Recap Realizing Synchrotron Radiation Properties • Wide-Band • High Brightness • Coherence • High energy, Low emittance stored electron beam • Optimized Insertion Devices June 2013 38 th Nathiagali Summer School

Coherent Emission of Synchrotron Radiation: when 1+1=4 Electron bunch Emission from kth electron: z s Total power Form Factor Gaussian bunch June 2013 38 th Nathiagali Summer School

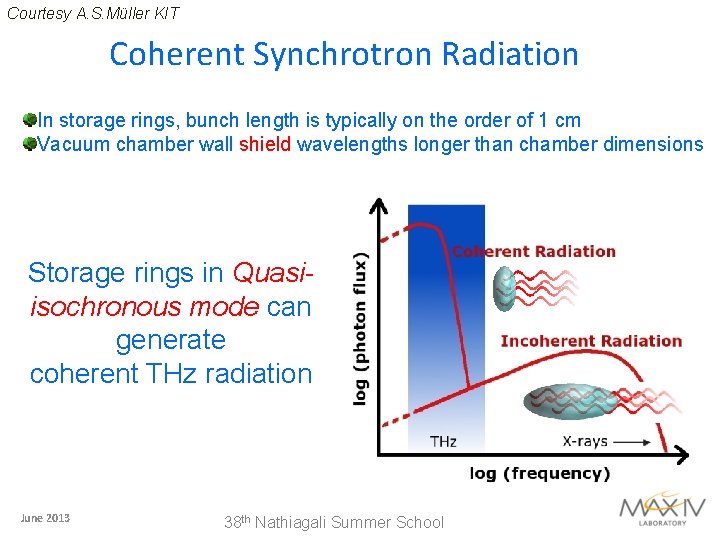
Courtesy A. S. Müller KIT Coherent Synchrotron Radiation In storage rings, bunch length is typically on the order of 1 cm Vacuum chamber wall shield wavelengths longer than chamber dimensions Storage rings in Quasiisochronous mode can generate coherent THz radiation June 2013 38 th Nathiagali Summer School

Courtesy A. S. Müller KIT Coherent THz Radiation At ANKA Q. I. mode Setup of beam line and detector : measurement behind a Si or Ca. F 2 vacuum window room temperature pneumatic (Golay) detector and aperture are mounted on a x-y imaging stage and scanned vs distance and lateral position relative to the vacuum window June 2013 38 th Nathiagali Summer School

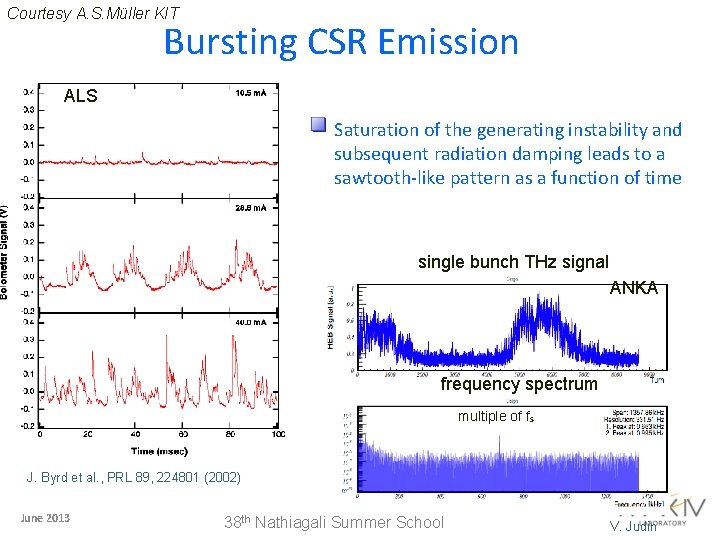
Courtesy A. S. Müller KIT Bursting CSR Emission ALS Saturation of the generating instability and subsequent radiation damping leads to a sawtooth-like pattern as a function of time single bunchspectrum THz signal frequency ANKA frequency spectrum multiple of fs J. Byrd et al. , PRL 89, 224801 (2002) June 2013 38 th Nathiagali Summer School V. Judin

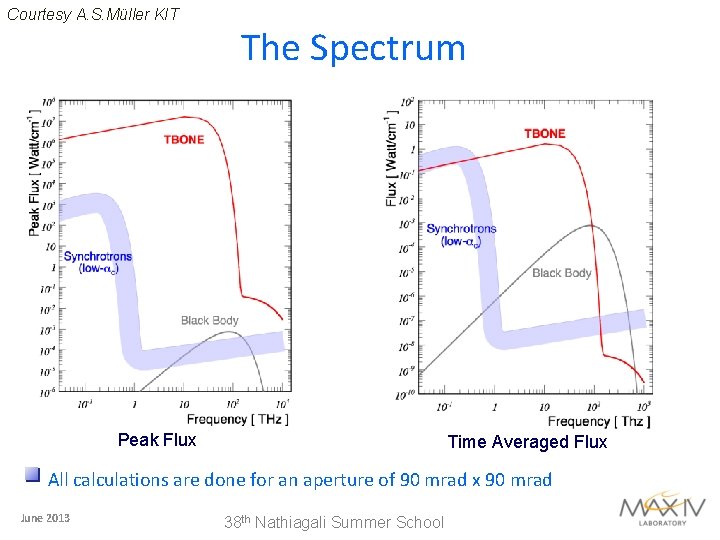
Courtesy A. S. Müller KIT The Spectrum Peak Flux Time Averaged Flux All calculations are done for an aperture of 90 mrad x 90 mrad June 2013 38 th Nathiagali Summer School

Free Electron Lasers Making Instabilities work for you E-beam emits radiation in the undulator. Radiation interacts with the beam generating energy and then density modulations – electrons group together in micro-bunches. The grouped electrons radiate in-phase leading to an increase of the fields. Field amplitude grows exponentially up to saturation C. Pellegrini, J. Stör, Beamline Vol. 32 N. 1, 2002 June 2013 38 th Nathiagali Summer School

Free Electron Lasers Various possible configurations Oscillator/Amplifier/SASE High-Gain Harmonic-Generation Free-Electron Laser, L. H. Yu et al, Science Vol. 289 p. 932 (2000) June 2013 38 th Nathiagali Summer School

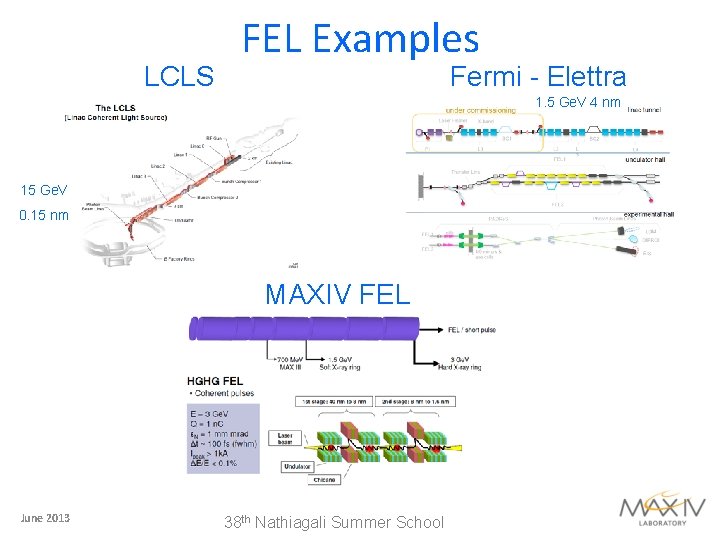
LCLS FEL Examples Fermi - Elettra 1. 5 Ge. V 4 nm 15 Ge. V 0. 15 nm MAXIV FEL June 2013 38 th Nathiagali Summer School

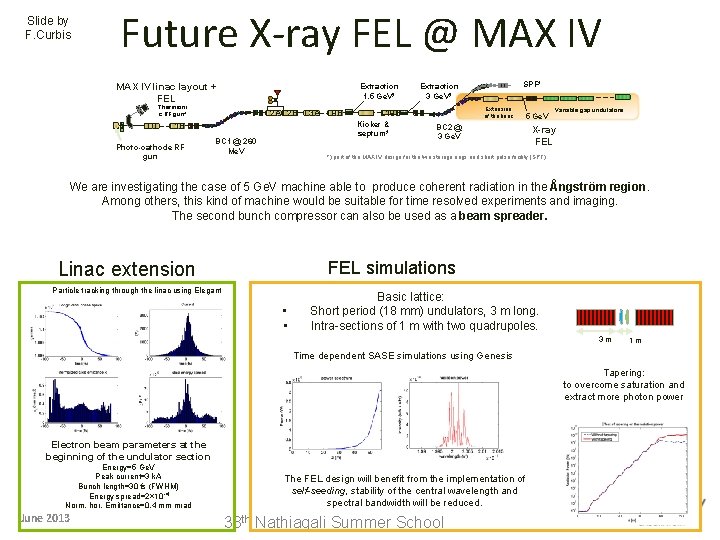
Slide by F. Curbis Future X-ray FEL @ MAX IV linac layout + FEL Extraction 1. 5 Ge. V* Thermioni c RF gun* L 0 L 2 AL 2 B L 3 A L 9 B L 1 B Photo-cathode RF gun BC 1 @ 260 Me. V Extension of the linac L 19 B Kicker & septum* SPF* Extraction 3 Ge. V* 5 Ge. V BC 2 @ 3 Ge. V Variable gap undulators X-ray FEL *) part of the MAX IV design for the two storage rings and short pulse facility (SPF) We are investigating the case of 5 Ge. V machine able to produce coherent radiation in the Ångström region. Among others, this kind of machine would be suitable for time resolved experiments and imaging. The second bunch compressor can also be used as a beam spreader. FEL simulations Linac extension Particle tracking through the linac using Elegant • • Basic lattice: Short period (18 mm) undulators, 3 m long. Intra-sections of 1 m with two quadrupoles. 3 m 1 m Time dependent SASE simulations using Genesis Tapering: to overcome saturation and extract more photon power Electron beam parameters at the beginning of the undulator section Energy=5 Ge. V Peak current=3 k. A Bunch length=30 fs (FWHM) Energy spread=2× 10 -4 Norm. hor. Emittance=0. 4 mm mrad June 2013 The FEL design will benefit from the implementation of self-seeding, stability of the central wavelength and spectral bandwidth will be reduced. 38 th Nathiagali Summer School

Free Electron Lasers Pros&Cons In LINACS: – – – Emittance and pulse length limited only by source properties. High brightness short pulses and coherence Relatively few light ports (high cost per experiment) Wave length limitations (mirror, availability of seed lasers). Low repetition rates (SC technology). In rings: – – – Natural synchronization (Pump and Probe) High repetition rate. Share the e-beam with many other users. Limited gain. Wavelength limitations June 2013 38 th Nathiagali Summer School

Energy Recovery LINACS Use a high quality beam from a LINAC and radiation from several undulators reaching high repetion rates by recovering the energy from the electrons Rings : recirculates the beam ERLs: recovers the energy but throws away the electrons June 2013 38 th Nathiagali Summer School

And that´s all for today…. . Thank you for your attention ! June 2013 38 th Nathiagali Summer School