The Physics of Cosmic Ray Acceleration Tony Bell

The Physics of Cosmic Ray Acceleration Tony Bell University of Oxford with Brian Reville Klara Schure Gwenael Giacinti Anabella Araudo Katherine Blundell SN 1006: A supernova remnant 7, 000 light years from Earth X-ray (blue): NASA/CXC/Rutgers/G. Cassam-Chenai, J. Hughes et al; Radio (red): NRAO/AUI/GBT/VLA/Dyer, Maddalena & Cornwell; Optical (yellow/orange): Middlebury College/F. Winkler. NOAO/AURA/NSF/CTIO Schmidt & DSS

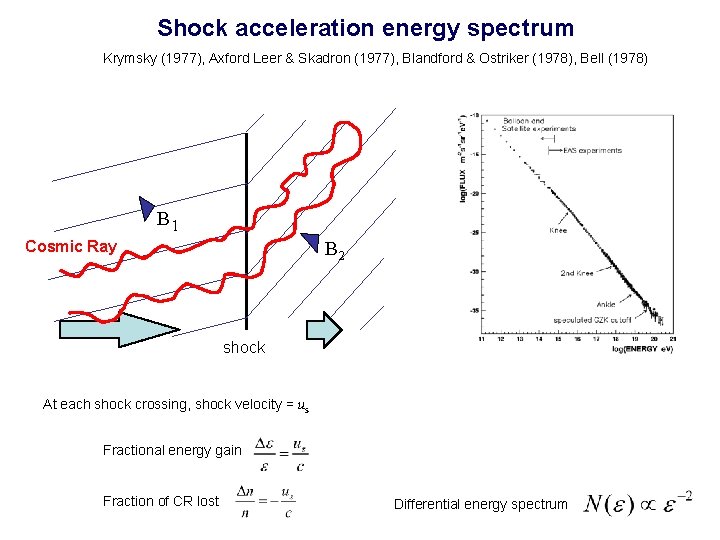
Shock acceleration energy spectrum Krymsky (1977), Axford Leer & Skadron (1977), Blandford & Ostriker (1978), Bell (1978) B 1 B 2 Cosmic Ray shock Low velocity High velocity plasma At each shock crossing, shock velocity = u s Fractional energy gain Fraction of CR lost Differential energy spectrum

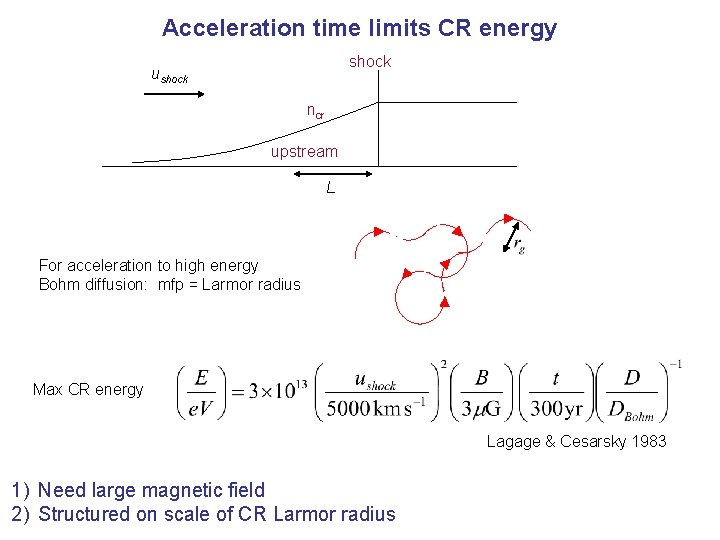
Acceleration time limits CR energy shock ushock ncr upstream L For acceleration to high energy Bohm diffusion: mfp = Larmor radius Max CR energy Lagage & Cesarsky 1983 1) Need large magnetic field 2) Structured on scale of CR Larmor radius

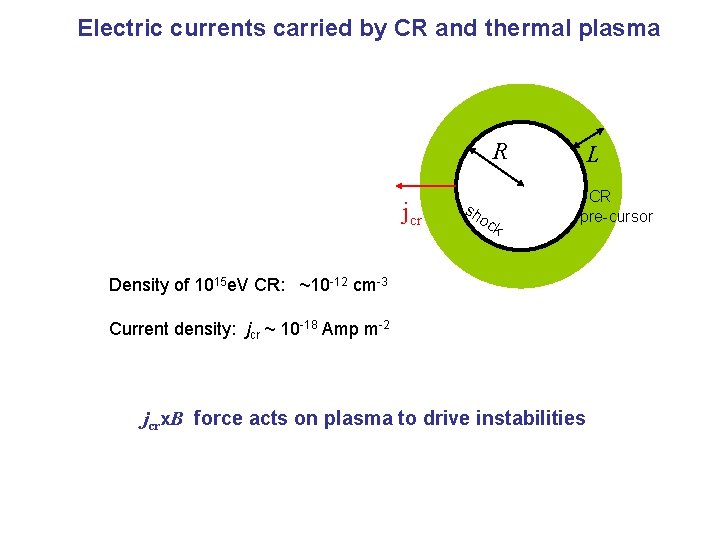
Electric currents carried by CR and thermal plasma R jcr sh oc k L CR pre-cursor Density of 1015 e. V CR: ~10 -12 cm-3 Current density: jcr ~ 10 -18 Amp m-2 jcrx. B force acts on plasma to drive instabilities

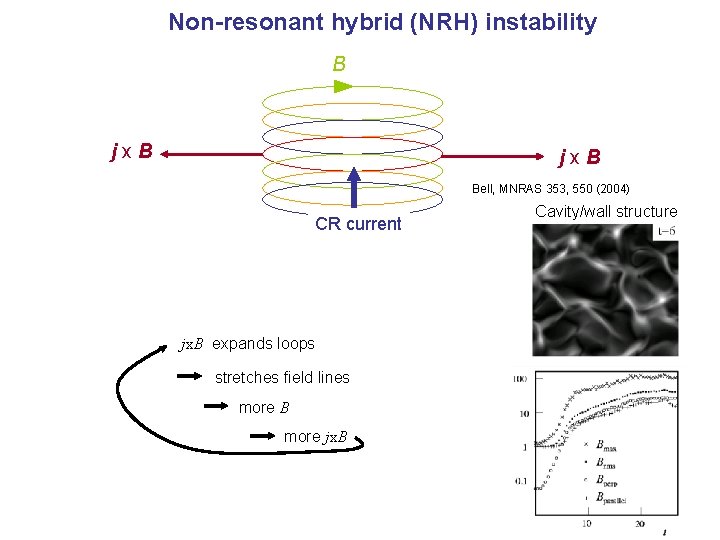
Non-resonant hybrid (NRH) instability B jx. B Bell, MNRAS 353, 550 (2004) CR current jx. B expands loops stretches field lines more B more jx. B Cavity/wall structure

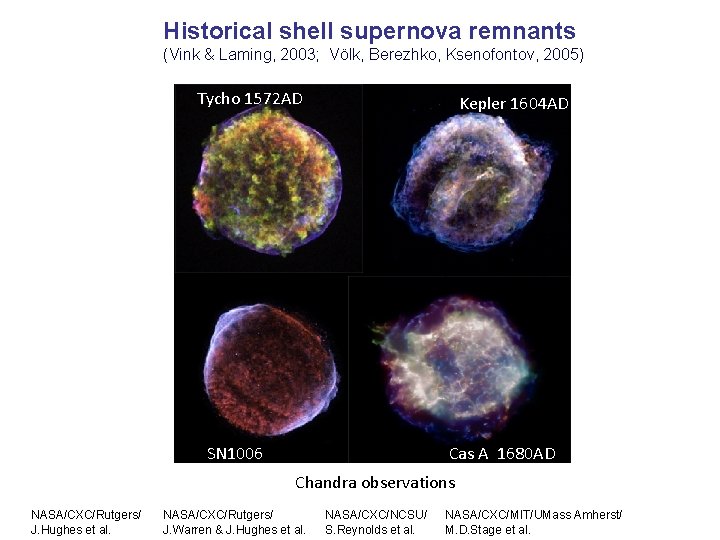
Historical shell supernova remnants (Vink & Laming, 2003; Völk, Berezhko, Ksenofontov, 2005) Tycho 1572 AD Kepler 1604 AD SN 1006 Cas A 1680 AD Chandra observations NASA/CXC/Rutgers/ J. Hughes et al. NASA/CXC/Rutgers/ J. Warren & J. Hughes et al. NASA/CXC/NCSU/ S. Reynolds et al. NASA/CXC/MIT/UMass Amherst/ M. D. Stage et al.

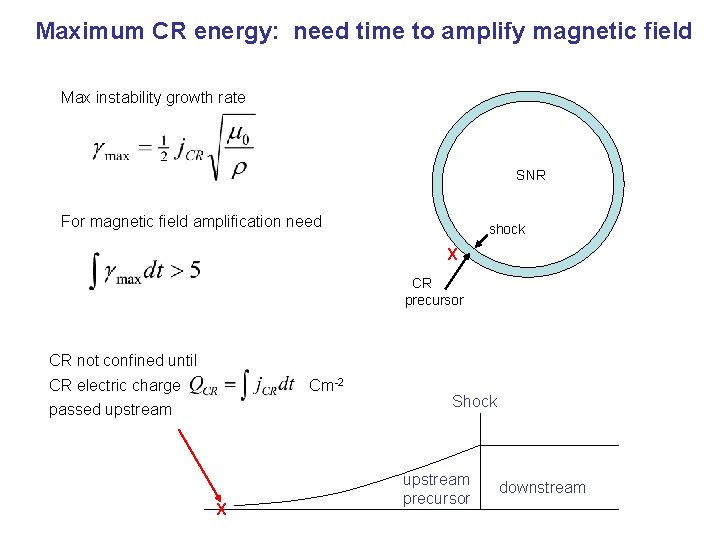
Maximum CR energy: need time to amplify magnetic field Max instability growth rate SNR For magnetic field amplification need shock X CR precursor CR not confined until CR electric charge Cm-2 passed upstream X Shock upstream precursor downstream

Maximum CR energy: need time to amplify magnetic field Cas A Already too slow Sedov phase shock vel in 1000 km s-1 Blast wave energy in 1044 J SN expansion into circumstellar wind shock vel in 30, 000 km s-1 wind mass loss in 10 -5 solar masses yr-1 wind vel in 10 km s-1

CR need to escape efficiently into ISM 90% of CR energy confined with Low energy CR cool adiabatically as SNR expands Energy drives blast wave Given to new generation of CR 10% of CR energy escapes with

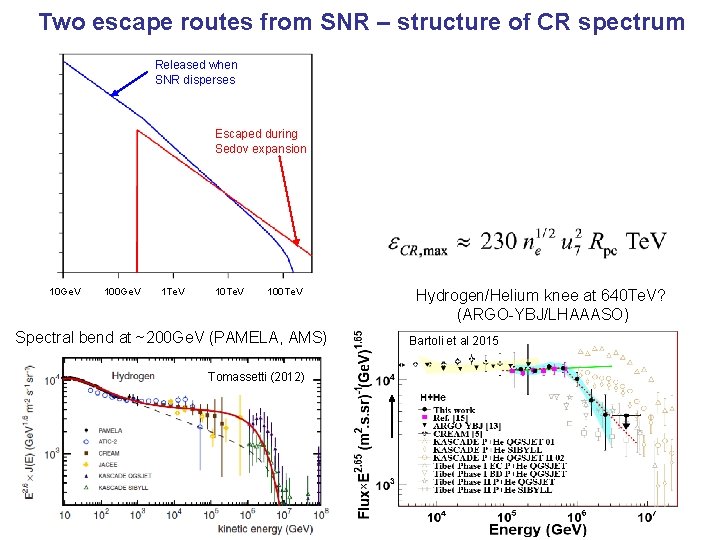
Two escape routes from SNR – structure of CR spectrum Released when SNR disperses Escaped during Sedov expansion 10 Ge. V 100 Ge. V 1 Te. V 100 Te. V Spectral bend at ~200 Ge. V (PAMELA, AMS) Tomassetti (2012) Hydrogen/Helium knee at 640 Te. V? (ARGO-YBJ/LHAAASO) Bartoli et al 2015

Particle acceleration in radio galaxies Image Credit: X-ray: NASA/CXC/SAO; Optical: NASA/STSc. I; Radio: NSF/NRAO/AUI/VLA

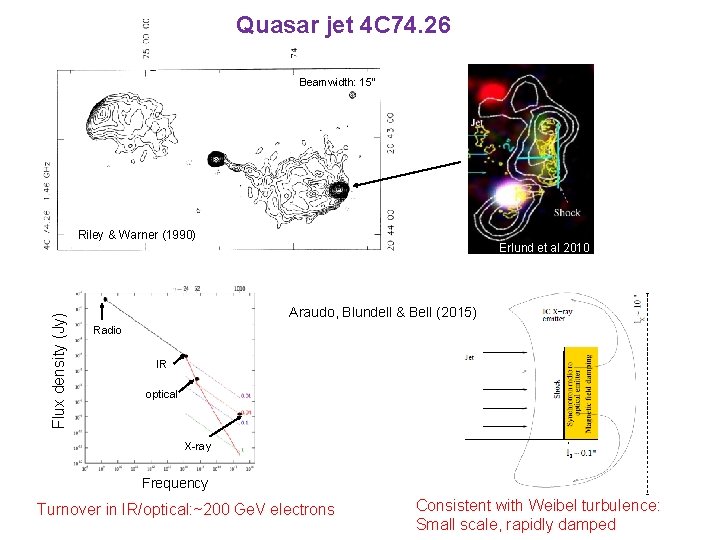
Quasar jet 4 C 74. 26 Beamwidth: 15” Flux density (Jy) Riley & Warner (1990) Erlund et al 2010 Erlund et et al al 2010 Erlund 2010 Araudo, Blundell & Bell (2015) Radio IR optical X-ray Frequency Turnover in IR/optical: ~200 Ge. V electrons Consistent with Weibel turbulence: Small scale, rapidly damped

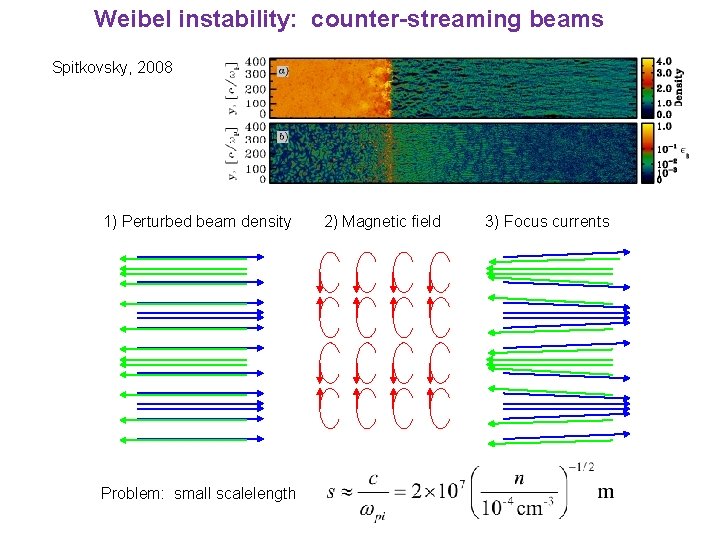
Weibel instability: counter-streaming beams Spitkovsky, 2008 1) Perturbed beam density Problem: small scalelength 2) Magnetic field 3) Focus currents

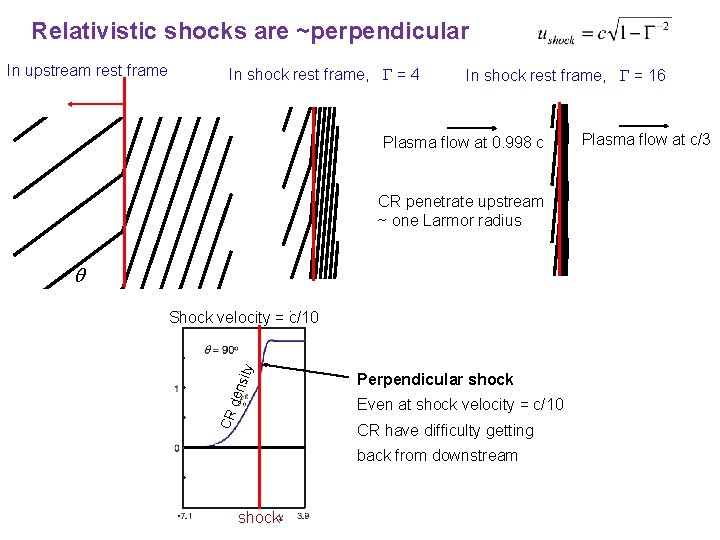
Relativistic shocks are ~perpendicular In upstream rest frame In shock rest frame, G = 4 In shock rest frame, G = 16 Plasma flow at 0. 998 c CR penetrate upstream ~ one Larmor radius q CR den sity Shock velocity = c/10 Perpendicular shock Even at shock velocity = c/10 CR have difficulty getting back from downstream shock Plasma flow at c/3

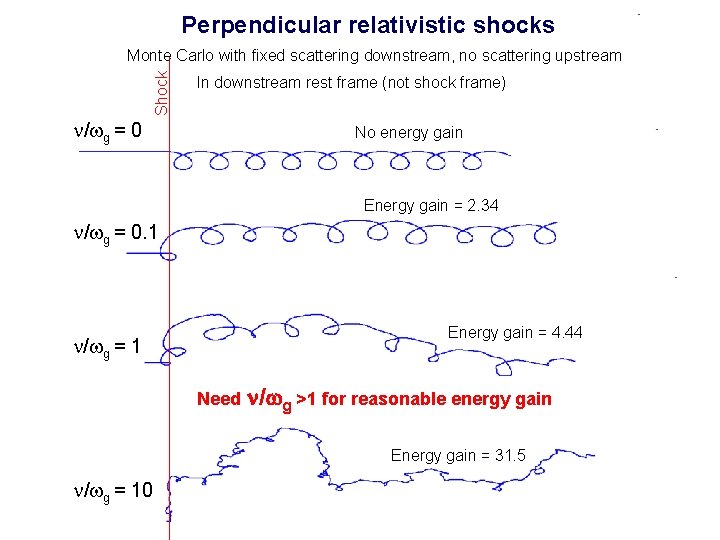
Perpendicular relativistic shocks Shock Monte Carlo with fixed scattering downstream, no scattering upstream In downstream rest frame (not shock frame) n/wg = 0 No energy gain Energy gain = 2. 34 n/wg = 0. 1 Energy gain = 4. 44 n/wg = 1 Need n/wg >1 for reasonable energy gain Energy gain = 31. 5 n/wg = 10

Limitations of Weibel instability Well-recognised Lemoine & Pelettier (2010), Sironi, Spitkovsky & Arons (2013), Reville & Bell (2014) Imagine turbulence consisting of random cells of size s Each cell deflects through angle Characteristic scalelength Larmor radius

Non-resonant hybrid (NRH) instability – can this help? Expands non-linearly, Condition for CR confinement: Disordered amplified magnetic field dominates initial field Maximum CR energy capable of exciting turbulence (assuming ~E-2. 4 CR spectrum) Turbulence can accelerate CR to higher energy

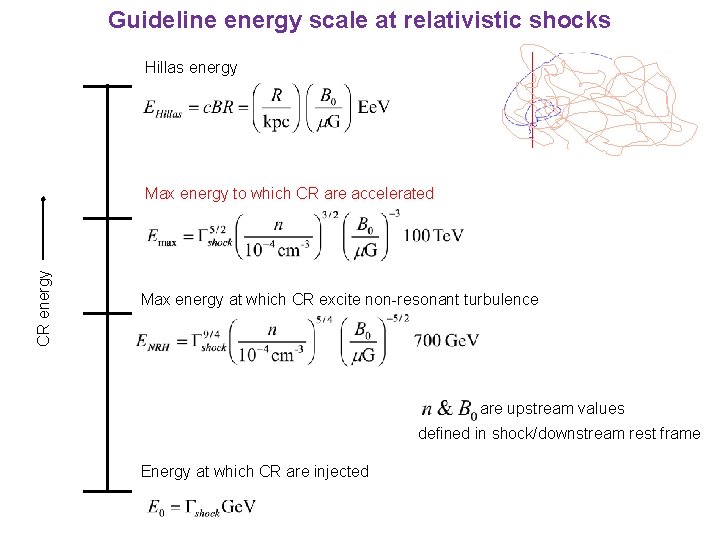
Guideline energy scale at relativistic shocks Hillas energy CR energy Max energy to which CR are accelerated Max energy at which CR excite non-resonant turbulence are upstream values defined in shock/downstream rest frame Energy at which CR are injected

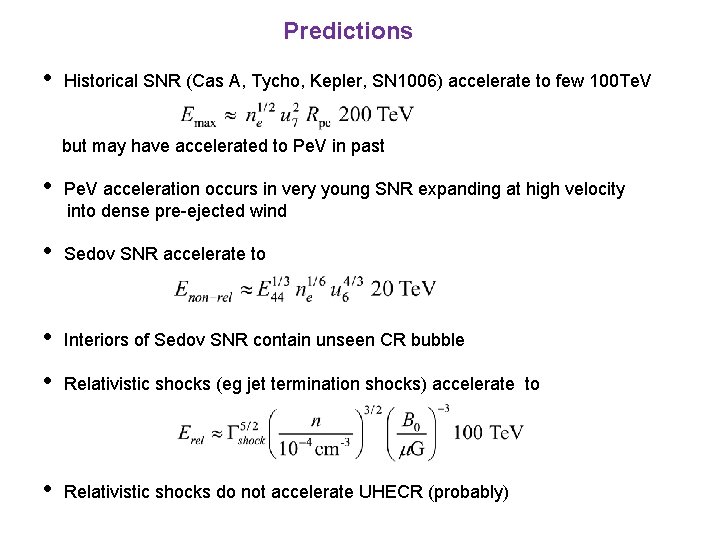
Predictions • Historical SNR (Cas A, Tycho, Kepler, SN 1006) accelerate to few 100 Te. V but may have accelerated to Pe. V in past • Pe. V acceleration occurs in very young SNR expanding at high velocity into dense pre-ejected wind • Sedov SNR accelerate to • Interiors of Sedov SNR contain unseen CR bubble • Relativistic shocks (eg jet termination shocks) accelerate to • Relativistic shocks do not accelerate UHECR (probably)