The photoelectric effect Contents Einsteins proposed experiment Solving

The photoelectric effect Contents: • Einstein’s proposed experiment • Solving photoelectric problems • Example 1 | Example 2 • Whiteboard • Photon vs wave theory

Light Waves Wavelength Changes Color small = blue Photons Energy per photon changes E = hf Radio waves vs X-rays big = red Amplitude Changes Brightness small = dim big = bright # of photons changes many = bright few = dim CCD Devices, High speed film

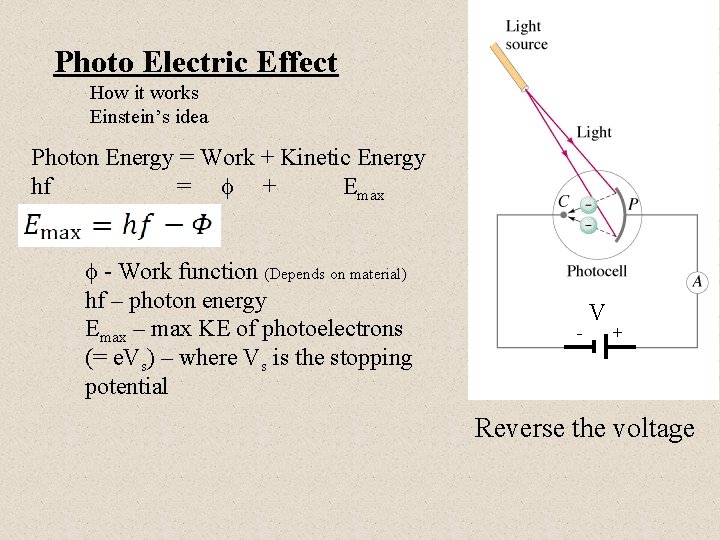
Photo Electric Effect How it works Einstein’s idea Photon Energy = Work + Kinetic Energy hf = + Emax - Work function (Depends on material) hf – photon energy Emax – max KE of photoelectrons (= e. Vs) – where Vs is the stopping potential - V + Reverse the voltage

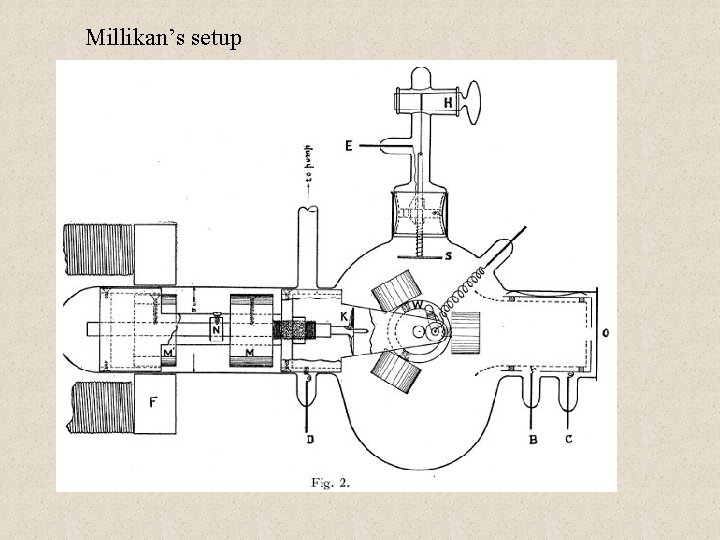
Millikan’s setup

Photon Energy = Work + Kinetic Energy hf = + Emax Example 1: A certain metal has a work function of 3. 25 e. V. When light of an unknown wavelength strikes it, the electrons have a stopping potential of 7. 35 V. What is the wavelength of the light? 117 nm

Photon Energy = Work + Kinetic Energy hf = + Emax Example 2: 70. 9 nm light strikes a metal with a work function of 5. 10 e. V. What is the maximum kinetic energy of the ejected photons in e. V? What is the stopping potential? 12. 4 V

Photon Energy = Work + Kinetic Energy hf = + Emax hf = hfo + e. V - Work function (Depends on material) fo - Lowest frequency that ejects e - Electron charge V - The uh stopping potential Example 1: A certain metal has a work function of 3. 25 e. V. When light of an unknown wavelength strikes it, the electrons have a stopping potential of 7. 35 V. What is the wavelength of the light? Photon energy = Work + Kinetic Energy Photon Energy = 3. 25 e. V + 7. 35 e. V = 10. 60 e. V Convert to J: (10. 60 e. V)(1. 602 E-19 J/e. V) = 1. 69812 E-18 J E = hf = hc/ , = hc/E = (6. 626 E-34 Js)(3. 00 E 8 m/s)/(1. 69812 E-18 J) = 1. 17059 E-07 m = 117 nm

Photon Energy = Work + Kinetic Energy hf = + Emax hf = hfo + e. V - Work function (Depends on material) fo - Lowest frequency that ejects e - Electron charge V - The uh stopping potential Example 2: 70. 9 nm light strikes a metal with a work function of 5. 10 e. V. What is the maximum kinetic energy of the ejected photons in e. V? What is the stopping potential? E = hf = hc/ = (6. 626 E-34 Js)(3. 00 E 8 m/s)/(70. 9 E-9) = 2. 80367 E-18 J Convert to e. V: (2. 80367 E-18 J)/(1. 602 E-19 J/e. V) = 17. 5 e. V Photon Energy = Work + Kinetic Energy 17. 5 e. V = 5. 10 + Kinetic Energy = 12. 4 e. V, so 12. 4 V would stop the electrons.

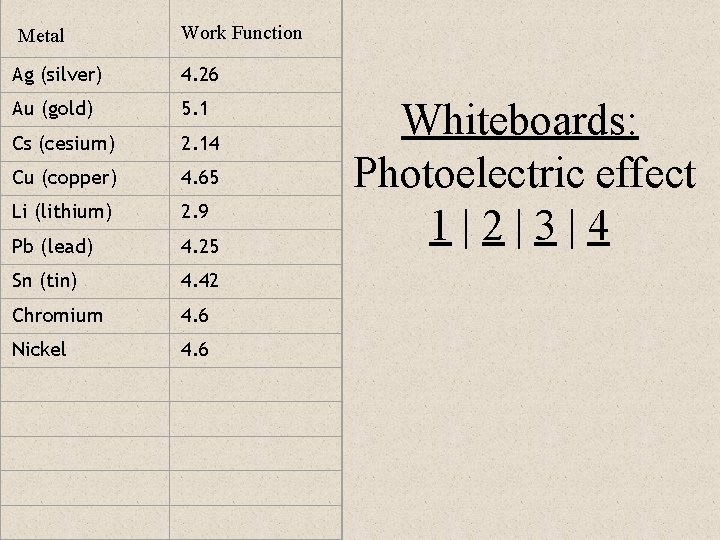
Metal Work Function Ag (silver) 4. 26 Au (gold) 5. 1 Cs (cesium) 2. 14 Cu (copper) 4. 65 Li (lithium) 2. 9 Pb (lead) 4. 25 Sn (tin) 4. 42 Chromium 4. 6 Nickel 4. 6 Whiteboards: Photoelectric effect 1|2|3|4

Photons of a certain energy strike a metal with a work function of 2. 15 e. V. The ejected electrons have a kinetic energy of 3. 85 e. V. (A stopping potential of 3. 85 V) What is the energy of the incoming photons in e. V? Photon energy = Work function + Kinetic energy of electron Photon energy = 2. 15 e. V + 3. 85 e. V = 6. 00 e. V

Another metal has a work function of 3. 46 e. V. What is the wavelength of light that ejects electrons with a stopping potential of 5. 00 V? (2) E = hf = hc/ , Photon energy = Work function + Kinetic energy of electron Photon energy = 3. 46 e. V + 5. 00 e. V = 8. 46 e. V E = (8. 46 e. V)(1. 602 x 10 -19 J/e. V) = 1. 3553 x 10 -18 J E = hf = hc/ , = hc/E = (6. 626 x 10 -34 Js)(3. 00 x 108 m/s)/(1. 3553 x 10 -18 J) = 1. 4667 x 10 -07 m = 147 nm

112 nm light strikes a metal with a work function of 4. 41 e. V. What is the stopping potential of the ejected electrons? (2) E = hf = hc/ , 1 e. V = 1. 602 x 10 -19 J Photon energy = Work function + Kinetic energy of electron E = hf = hc/ = (6. 626 x 10 -34 Js)(3. 00 x 108 m/s)/(112 x 10 -9 m) E = 1. 7748 x 10 -18 J E = (1. 7748 x 10 -18 J)/(1. 602 x 10 -19 J/e. V) = 11. 079 e. V Photon energy = Work function + Kinetic energy of electron 11. 079 e. V = 4. 41 e. V + e. Vs 11. 079 e. V - 4. 41 e. V = 6. 6688 e. V = e. Vs Vs = 6. 67 V

256 nm light strikes a metal and the ejected electrons have a stopping potential of 1. 15 V. What is the work function of the metal in e. V? (2) E = hf = hc/ , 1 e. V = 1. 602 x 10 -19 J Photon energy = Work function + Kinetic energy of electron E = hf = hc/ = (6. 626 x 10 -34 Js)(3. 00 x 108 m/s)/(256 x 10 -9 m) E = 7. 7648 x 10 -19 J E = (7. 7648 x 10 -19 J)/(1. 602 x 10 -19 J/e. V) = 4. 847 e. V Photon energy = Work function + Kinetic energy of electron 4. 847 e. V = Work function + 1. 15 e. V 11. 079 e. V - 1. 15 e. V = 3. 70 e. V

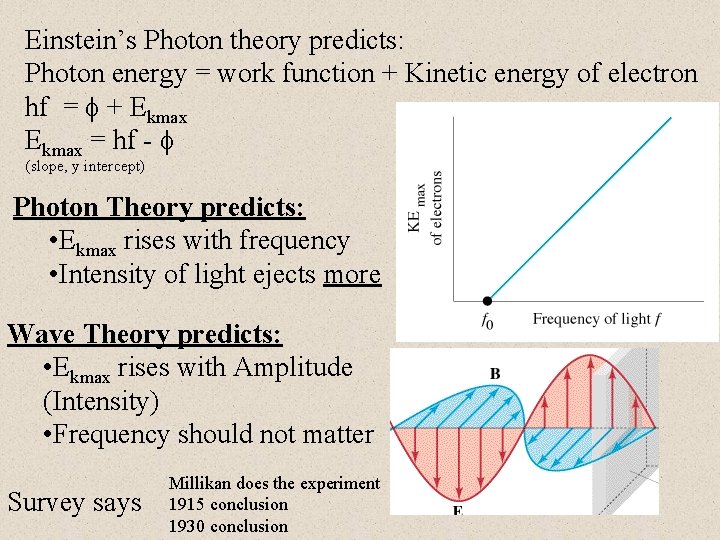
Einstein’s Photon theory predicts: Photon energy = work function + Kinetic energy of electron hf = + Ekmax = hf - (slope, y intercept) Photon Theory predicts: • Ekmax rises with frequency • Intensity of light ejects more Wave Theory predicts: • Ekmax rises with Amplitude (Intensity) • Frequency should not matter Survey says Millikan does the experiment 1915 conclusion 1930 conclusion