The Petri Net Method By Dr Chris Ling

The Petri Net Method By Dr Chris Ling School of Computer Science & Software Engineering Monash University Chris. Ling@csse. monash. edu. au

Introduction 4 First introduced by Carl Adam Petri in 1962. 4 A diagrammatic tool to model concurrency and synchronization in distributed systems. 4 Very similar to State Transition Diagrams. 4 Used as a visual communication aid to model the system behaviour. 4 Based on strong mathematical foundation. (C) Copyright 2001, Chris Ling
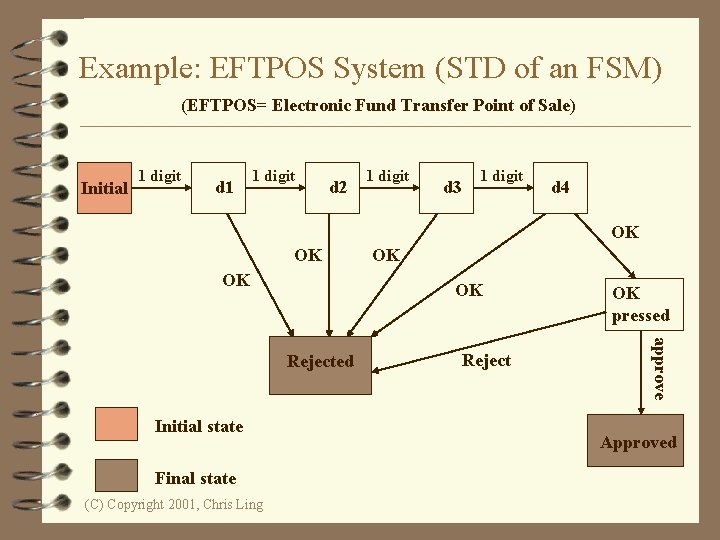
Example: EFTPOS System (STD of an FSM) (EFTPOS= Electronic Fund Transfer Point of Sale) Initial 1 digit d 1 1 digit d 2 1 digit d 3 1 digit d 4 OK OK Final state (C) Copyright 2001, Chris Ling Reject OK pressed approve Rejected Initial state OK Approved
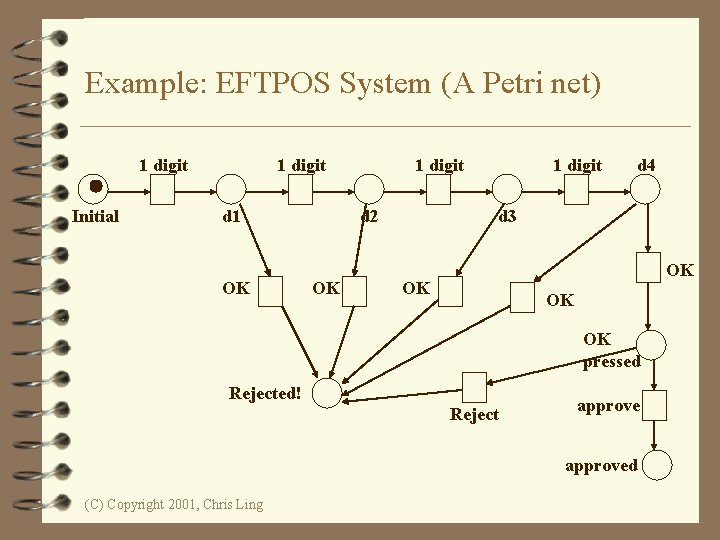
Example: EFTPOS System (A Petri net) 1 digit Initial 1 digit d 1 OK 1 digit d 2 OK 1 digit d 4 d 3 OK OK pressed Rejected! Reject approved (C) Copyright 2001, Chris Ling

EFTPOS System 4 Scenario 1: Normal – Enters all 4 digits and press OK. 4 Scenario 2: Exceptional – Enters only 3 digits and press OK. (C) Copyright 2001, Chris Ling
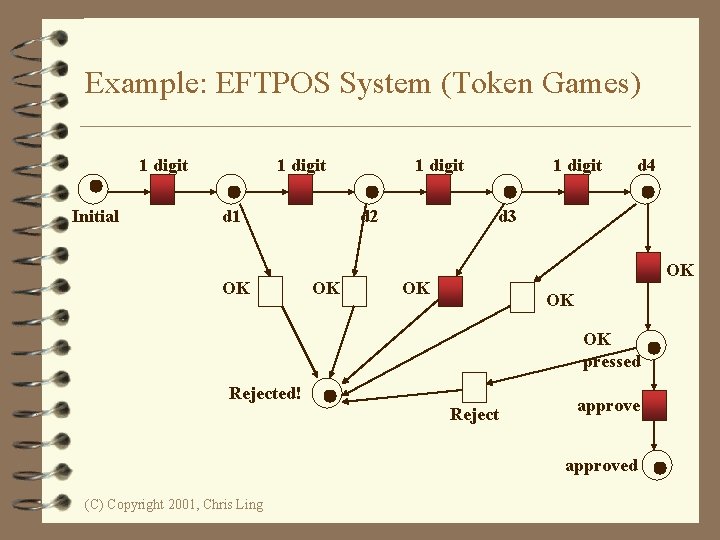
Example: EFTPOS System (Token Games) 1 digit Initial 1 digit d 1 OK 1 digit d 2 OK 1 digit d 4 d 3 OK OK pressed Rejected! Reject approved (C) Copyright 2001, Chris Ling

A Petri Net Specification. . . 4 consists of three types of components: places (circles), transitions (rectangles) and arcs (arrows): – Places represent possible states of the system; – Transitions are events or actions which cause the change of state; And – Every arc simply connects a place with a transition or a transition with a place. (C) Copyright 2001, Chris Ling

A Change of State … 4 is denoted by a movement of token(s) (black dots) from place(s) to place(s); and is caused by the firing of a transition. 4 The firing represents an occurrence of the event or an action taken. 4 The firing is subject to the input conditions, denoted by token availability. (C) Copyright 2001, Chris Ling

A Change of State 4 A transition is firable or enabled when there are sufficient tokens in its input places. 4 After firing, tokens will be transferred from the input places (old state) to the output places, denoting the new state. 4 Note that the EFTPOS example is a Petri net representation of a finite state machine (FSM). (C) Copyright 2001, Chris Ling

Example: Vending Machine 4 The machine dispenses two kinds of snack bars – 20 c and 15 c. 4 Only two types of coins can be used – 10 c coins and 5 c coins. 4 The machine does not return any change. (C) Copyright 2001, Chris Ling
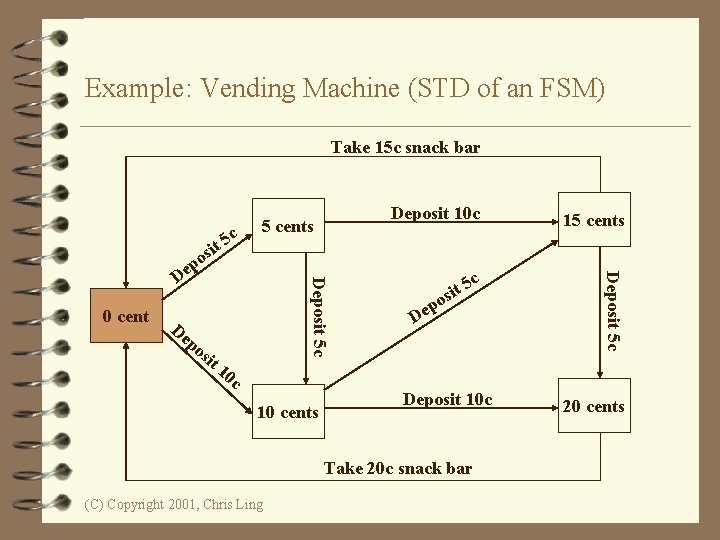
Example: Vending Machine (STD of an FSM) Take 15 c snack bar sit De po sit c t 5 i s o ep D 15 cents Deposit 5 c 0 cent Deposit 5 c po e D 5 c Deposit 10 c 5 cents 10 cents Deposit 10 c Take 20 c snack bar (C) Copyright 2001, Chris Ling 20 cents
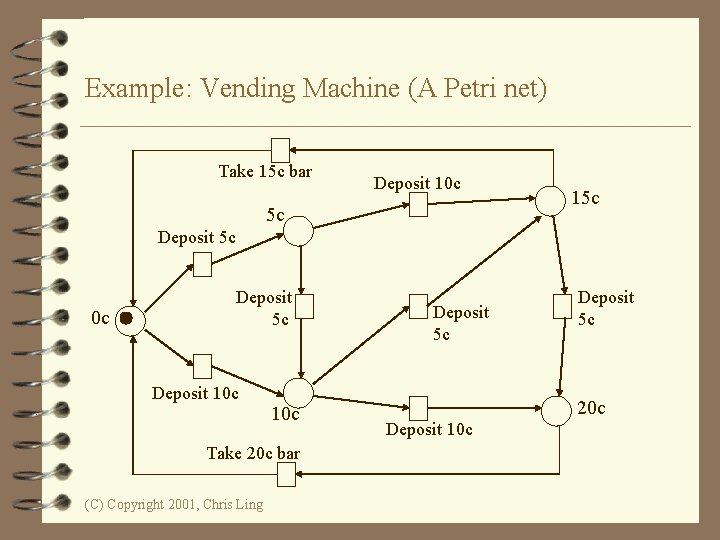
Example: Vending Machine (A Petri net) Take 15 c bar Deposit 10 c 5 c 15 c Deposit 5 c 0 c Deposit 5 c Deposit 10 c Take 20 c bar (C) Copyright 2001, Chris Ling Deposit 5 c 20 c Deposit 10 c

Example: Vending Machine (3 Scenarios) 4 Scenario 1: – Deposit 5 c, deposit 5 c, take 20 c snack bar. 4 Scenario 2: – Deposit 10 c, deposit 5 c, take 15 c snack bar. 4 Scenario 3: – Deposit 5 c, deposit 10 c, deposit 5 c, take 20 c snack bar. (C) Copyright 2001, Chris Ling
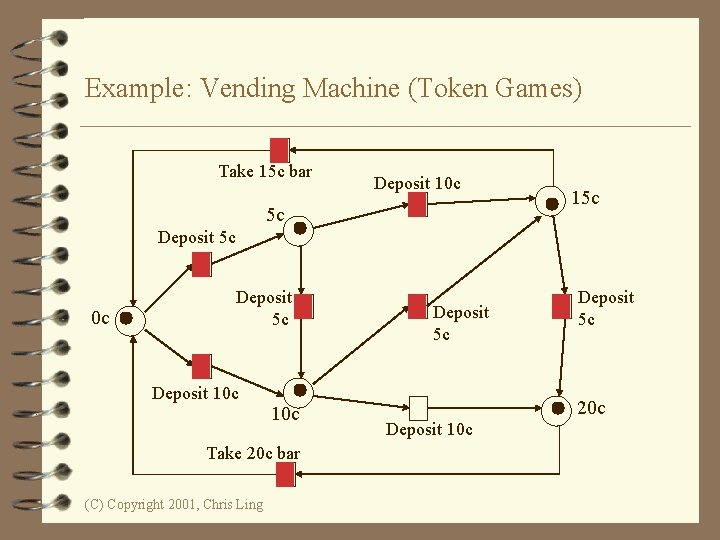
Example: Vending Machine (Token Games) Take 15 c bar Deposit 10 c 5 c 15 c Deposit 5 c 0 c Deposit 5 c Deposit 10 c Take 20 c bar (C) Copyright 2001, Chris Ling Deposit 5 c 20 c Deposit 10 c

Multiple Local States 4 In the real world, events happen at the same time. 4 A system may have many local states to form a global state. 4 There is a need to model concurrency and synchronization. (C) Copyright 2001, Chris Ling

Example: In a Restaurant (A Petri Net) Waiter free Customer 1 Customer 2 Take order wait eating Serve food (C) Copyright 2001, Chris Ling Order taken Tell kitchen wait eating Serve food
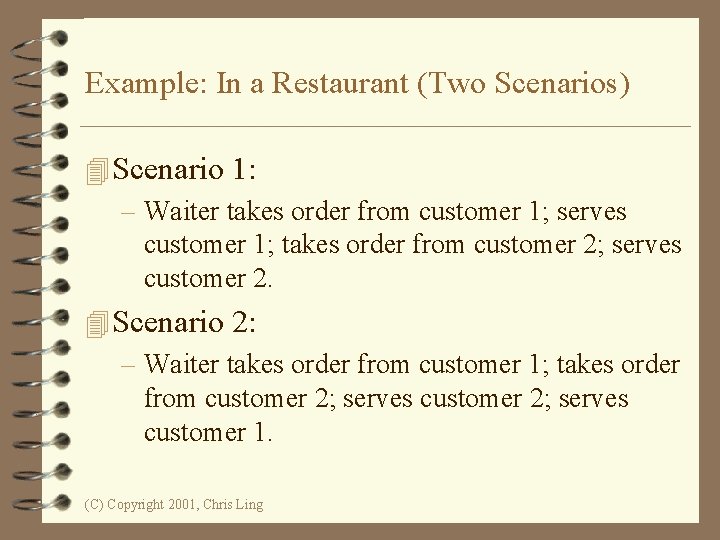
Example: In a Restaurant (Two Scenarios) 4 Scenario 1: – Waiter takes order from customer 1; serves customer 1; takes order from customer 2; serves customer 2. 4 Scenario 2: – Waiter takes order from customer 1; takes order from customer 2; serves customer 1. (C) Copyright 2001, Chris Ling
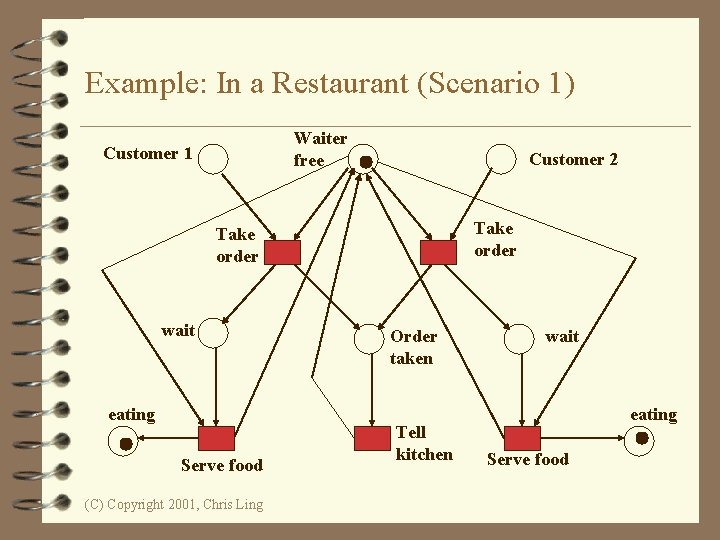
Example: In a Restaurant (Scenario 1) Waiter free Customer 1 Customer 2 Take order wait eating Serve food (C) Copyright 2001, Chris Ling Order taken Tell kitchen wait eating Serve food
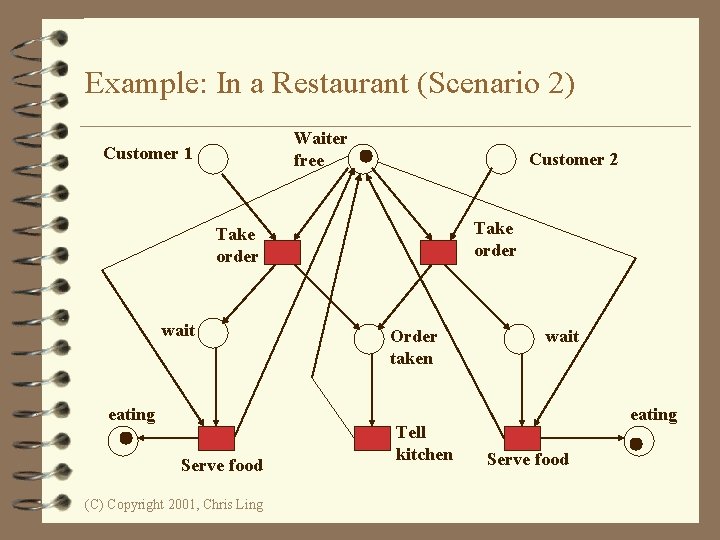
Example: In a Restaurant (Scenario 2) Waiter free Customer 1 Customer 2 Take order wait eating Serve food (C) Copyright 2001, Chris Ling Order taken Tell kitchen wait eating Serve food
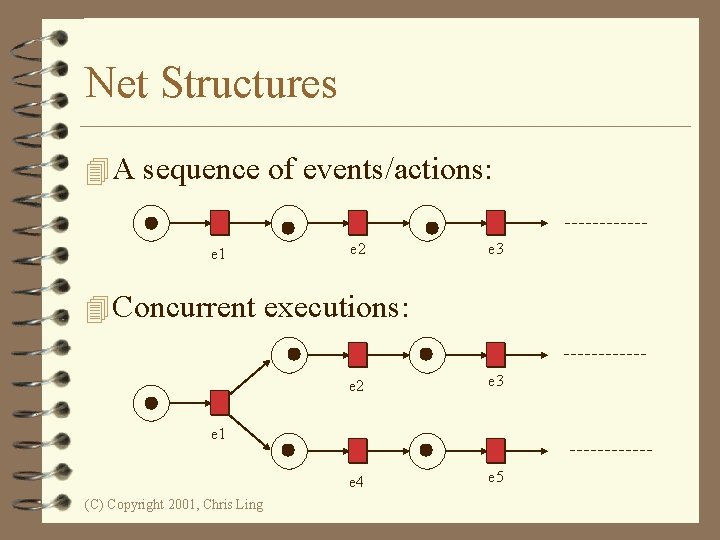
Net Structures 4 A sequence of events/actions: e 1 e 2 e 3 4 Concurrent executions: e 2 e 3 e 4 e 5 e 1 (C) Copyright 2001, Chris Ling
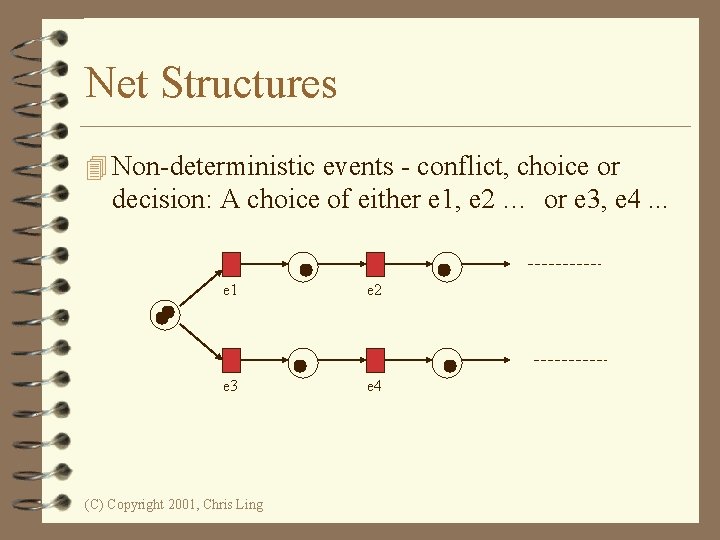
Net Structures 4 Non-deterministic events - conflict, choice or decision: A choice of either e 1, e 2 … or e 3, e 4. . . e 1 e 2 e 3 e 4 (C) Copyright 2001, Chris Ling
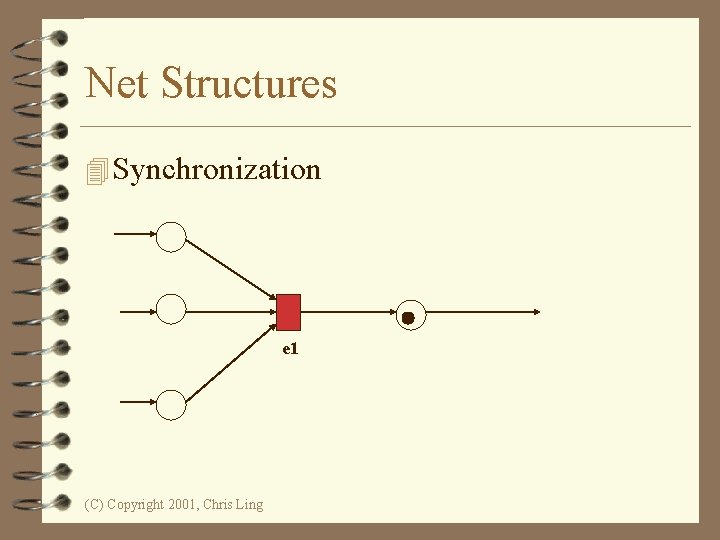
Net Structures 4 Synchronization e 1 (C) Copyright 2001, Chris Ling
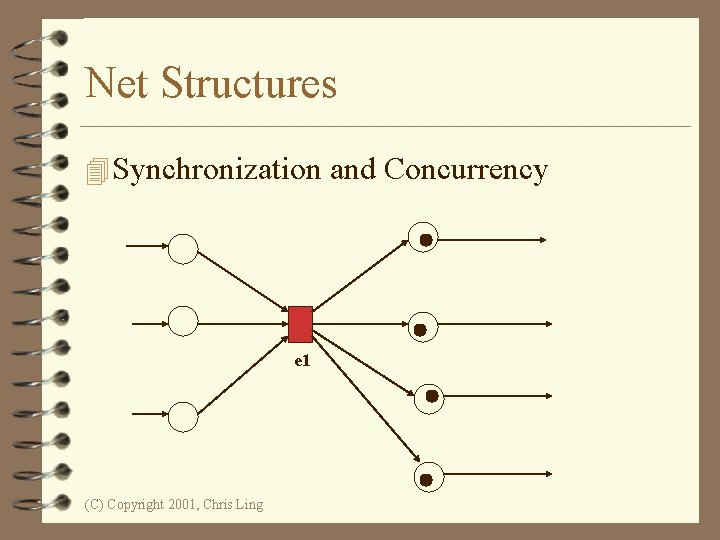
Net Structures 4 Synchronization and Concurrency e 1 (C) Copyright 2001, Chris Ling

Another Example • A producer-consumer system, consist of one producer, two consumers and one storage buffer with the following conditions: • The storage buffer may contain at most 5 items; • The producer sends 3 items in each production; • At most one consumer is able to access the storage buffer at one time; • Each consumer removes two items when accessing the storage buffer (C) Copyright 2001, Chris Ling
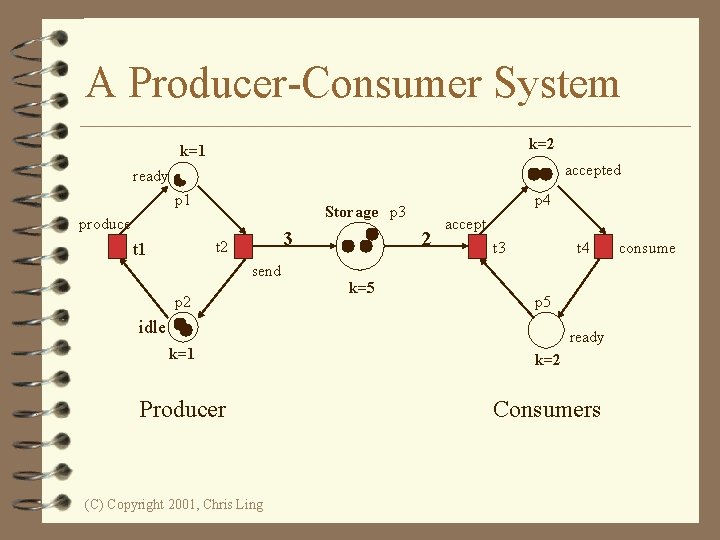
A Producer-Consumer System k=2 k=1 accepted ready p 1 produce 3 t 2 t 1 p 4 Storage p 3 send p 2 2 k=5 accept t 3 t 4 p 5 idle ready k=1 k=2 Producer Consumers (C) Copyright 2001, Chris Ling consume

A Producer-Consumer Example • In this Petri net, every place has a capacity and every arc has a weight. • This allows multiple tokens to reside in a place to model more complex behaviour. (C) Copyright 2001, Chris Ling

Behavioural Properties • Reachability • “Can we reach one particular state from another? ” • Boundedness • “Will a storage place overflow? ” • Liveness • “Will the system die in a particular state? ” (C) Copyright 2001, Chris Ling
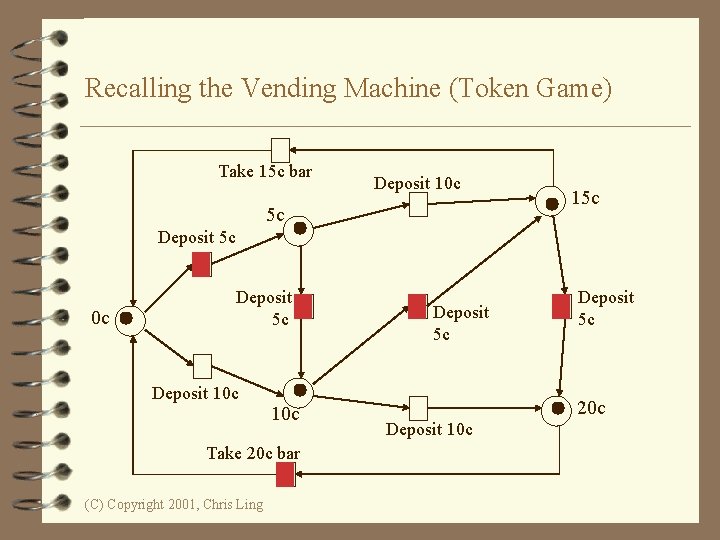
Recalling the Vending Machine (Token Game) Take 15 c bar Deposit 10 c 5 c 15 c Deposit 5 c 0 c Deposit 5 c Deposit 10 c Take 20 c bar (C) Copyright 2001, Chris Ling Deposit 5 c 20 c Deposit 10 c
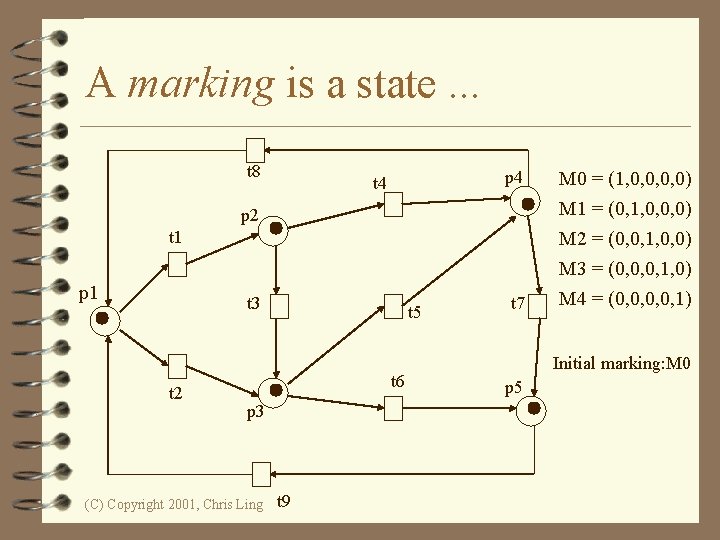
A marking is a state. . . t 8 t 4 p 4 M 0 = (1, 0, 0) M 1 = (0, 1, 0, 0, 0) M 2 = (0, 0, 1, 0, 0) M 3 = (0, 0, 0, 1, 0) t 7 M 4 = (0, 0, 1) p 2 t 1 p 1 t 3 t 2 t 5 t 6 p 3 (C) Copyright 2001, Chris Ling t 9 Initial marking: M 0 p 5
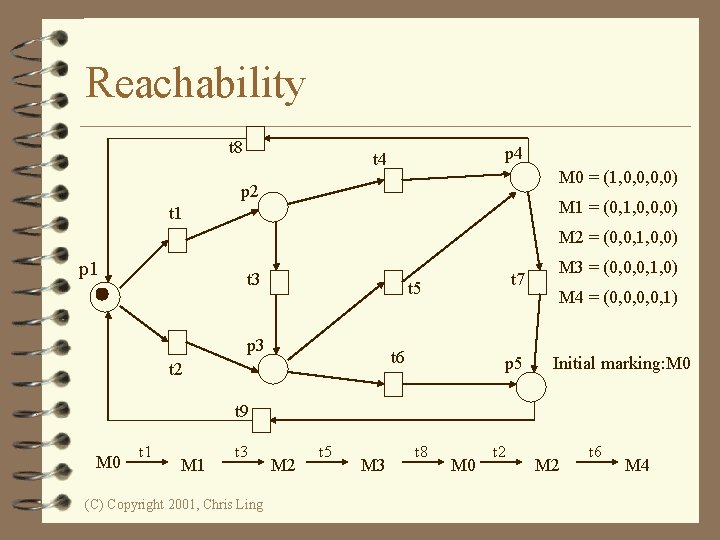
Reachability t 8 p 4 t 4 M 0 = (1, 0, 0) p 2 M 1 = (0, 1, 0, 0, 0) t 1 M 2 = (0, 0, 1, 0, 0) p 1 t 3 t 7 t 5 p 3 t 6 t 2 p 5 M 3 = (0, 0, 0, 1, 0) M 4 = (0, 0, 1) Initial marking: M 0 t 9 M 0 t 1 M 1 t 3 (C) Copyright 2001, Chris Ling M 2 t 5 M 3 t 8 M 0 t 2 M 2 t 6 M 4

Reachability A firing or occurrence sequence: M 0 t 1 M 1 t 3 M 2 t 5 M 3 t 8 M 0 t 2 M 2 t 6 M 4 • “M 2 is reachable from M 1 and M 4 is reachable from M 0. ” • In fact, in the vending machine example, all markings are reachable from every marking. (C) Copyright 2001, Chris Ling

Boundedness • A Petri net is said to be k-bounded or simply bounded if the number of tokens in each place does not exceed a finite number k for any marking reachable from M 0. • The Petri net for vending machine is 1 bounded. • A 1 -bounded Petri net is also safe. (C) Copyright 2001, Chris Ling

Liveness • A Petri net with initial marking M 0 is live if, no matter what marking has been reached from M 0, it is possible to ultimately fire any transition by progressing through some further firing sequence. • A live Petri net guarantees deadlock-free operation, no matter what firing sequence is chosen. (C) Copyright 2001, Chris Ling

Liveness • The vending machine is live and the producer-consumer system is also live. • A transition is dead if it can never be fired in any firing sequence. (C) Copyright 2001, Chris Ling
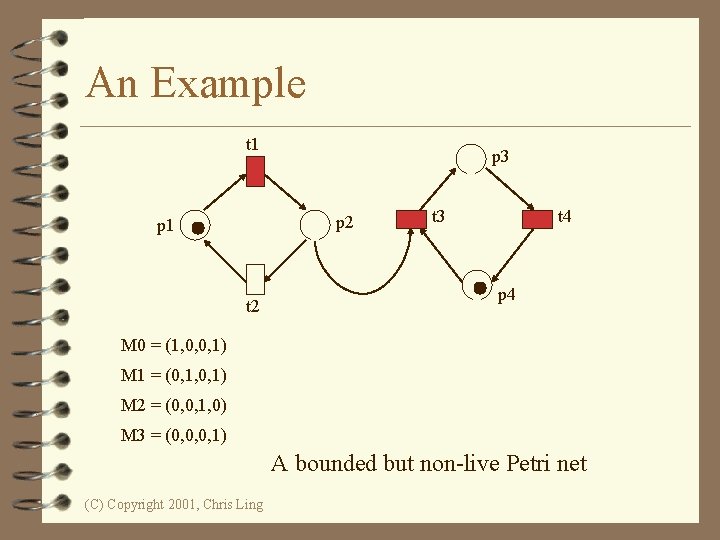
An Example t 1 p 3 p 2 p 1 t 2 t 3 t 4 p 4 M 0 = (1, 0, 0, 1) M 1 = (0, 1, 0, 1) M 2 = (0, 0, 1, 0) M 3 = (0, 0, 0, 1) A bounded but non-live Petri net (C) Copyright 2001, Chris Ling
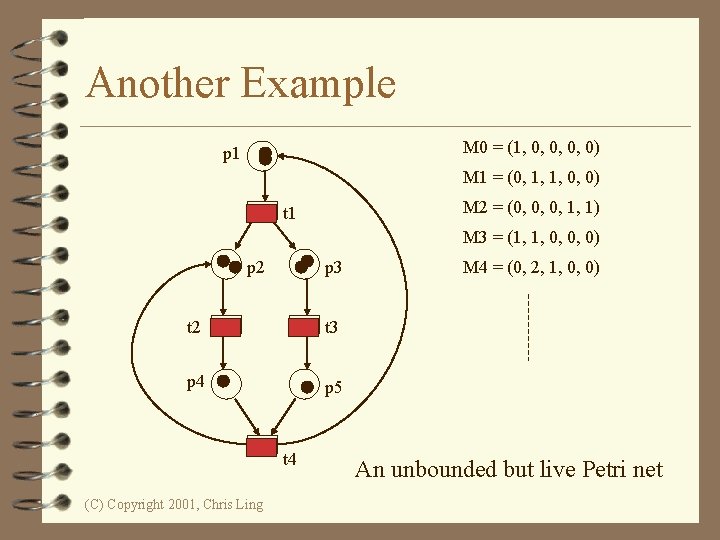
Another Example M 0 = (1, 0, 0) p 1 M 1 = (0, 1, 1, 0, 0) M 2 = (0, 0, 0, 1, 1) t 1 M 3 = (1, 1, 0, 0, 0) p 2 p 3 t 2 t 3 p 4 p 5 t 4 (C) Copyright 2001, Chris Ling M 4 = (0, 2, 1, 0, 0) An unbounded but live Petri net

Analysis Methods • Reachability Analysis: • Reachability or coverability tree. • State explosion problem. • Incidence Matrix and State Equations. • Structural Analysis • Based on net structures. (C) Copyright 2001, Chris Ling

Other Types of Petri Nets • High-level Petri nets • Tokens have “colours”, holding complex information. • Timed Petri nets • Time delays associated with transitions and/or places. • Fixed delays or interval delays. • Stochastic Petri nets: exponentially distributed random variables as delays. (C) Copyright 2001, Chris Ling

Other Types of Petri Nets • Object-Oriented Petri nets • Tokens are instances of classes, moving from one place to another, calling methods and changing attributes. • Net structure models the inner behaviour of objects. • The purpose is to use object-oriented constructs to structure and build the system. (C) Copyright 2001, Chris Ling
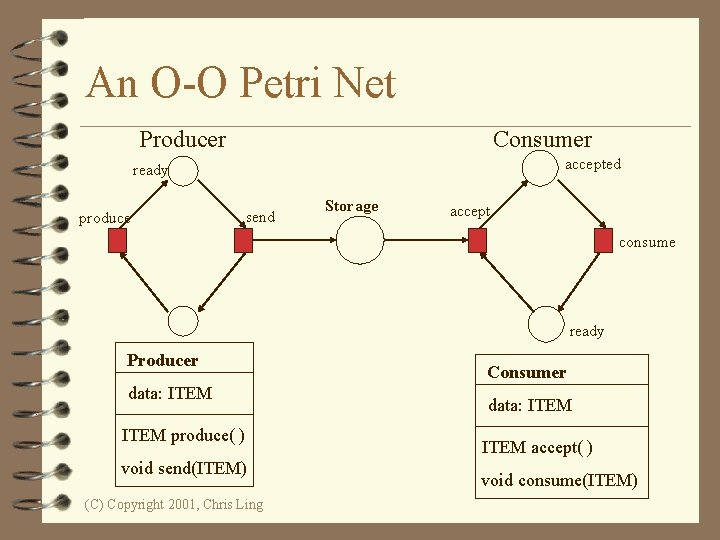
An O-O Petri Net Producer Consumer accepted ready produce send Storage accept consume ready Producer data: ITEM produce( ) void send(ITEM) (C) Copyright 2001, Chris Ling Consumer data: ITEM accept( ) void consume(ITEM)

Petri Net References i Murata, T. (1989, April). Petri nets: properties, analysis and applications. Proceedings of the IEEE, 77(4), 541 -80. i Peterson, J. L. (1981). Petri Net Theory and the Modeling of Systems. Prentice-Hall. i Reisig, W and G. Rozenberg (eds) (1998). Lectures on Petri Nets 1: Basic Models. Springer-Verlag. i The World of Petri nets: http: //www. daimi. au. dk/Petri. Nets/ (C) Copyright 2001, Chris Ling
- Slides: 41