The Parent Function can be transformed by using

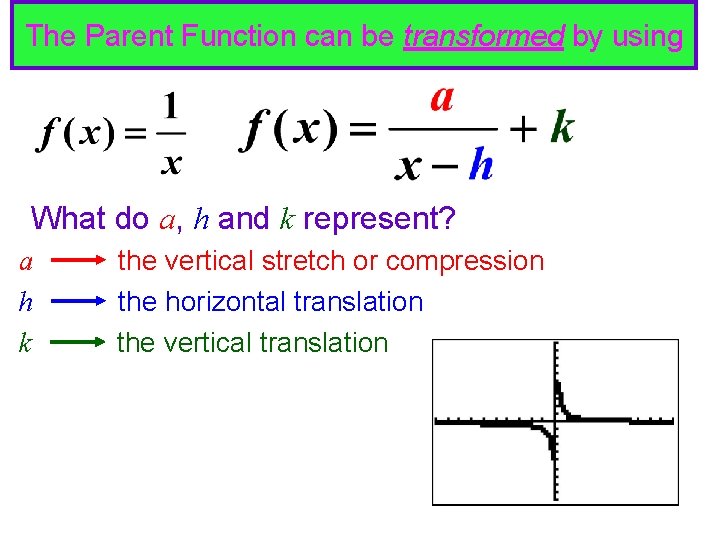
The Parent Function can be transformed by using What do a, h and k represent? a h k the vertical stretch or compression the horizontal translation the vertical translation

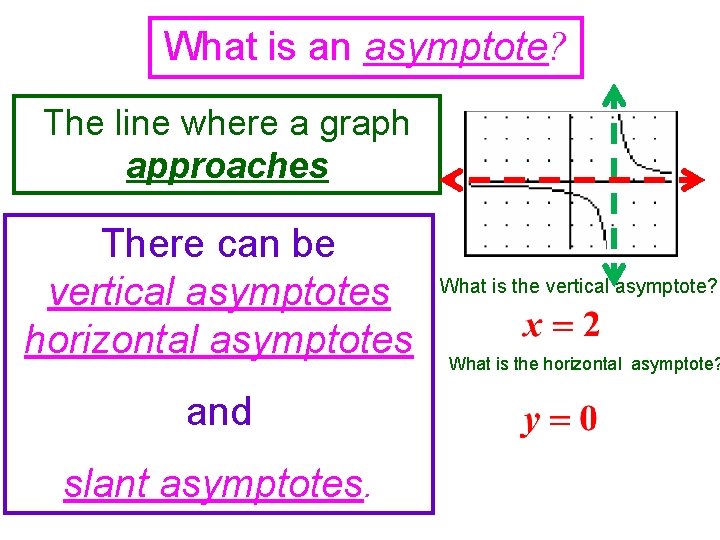
What is an asymptote? The line where a graph approaches There can be vertical asymptotes horizontal asymptotes and slant asymptotes. What is the vertical asymptote? What is the horizontal asymptote?

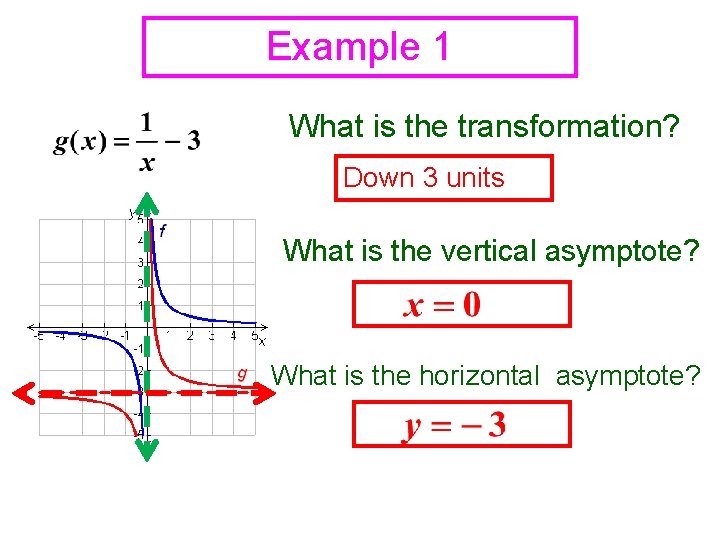
Example 1 What is the transformation? Down 3 units What is the vertical asymptote? What is the horizontal asymptote?

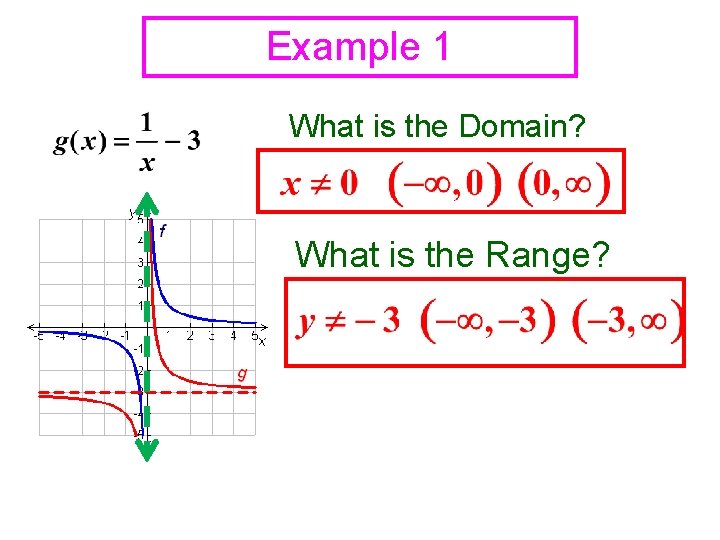
Example 1 What is the Domain? What is the Range?

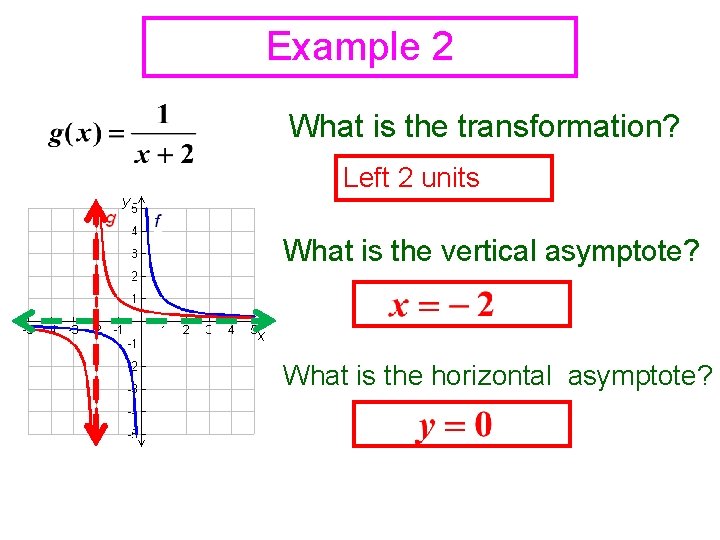
Example 2 What is the transformation? Left 2 units What is the vertical asymptote? What is the horizontal asymptote?

To Graph Rational Functions 1. Factor Completely 2. Vertical Asymptotes: set the denominator equal to zero. It is stated as an equation The vertical asymptotes are the domain exclusions. • 3. Horizontal Asymptotes: compare the degrees of the numerator and denominator.

Horizontal Asymptote If then HA: y = 0 If you look at then HA: y = 2 If then there is NO horizontal asymptote HA: none

Graphing continued 4. Roots: set the numerator = 0 What is another name for the x-intercepts? Roots What does it mean on the graph? Where the graph crosses the x-axis

Graphing continued 5. Holes: Look at factors that are common to numerator and denominator. Set those equal to 0 and solve. Vertical Asymptotes do NOT include the holes.

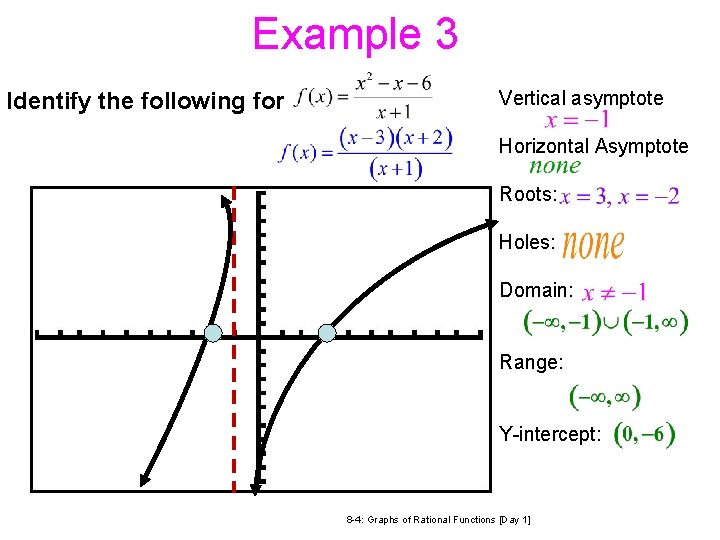
Example 3 Identify the following for Vertical asymptote Horizontal Asymptote Roots: Holes: Domain: Range: Y-intercept: 12/23/2021 3: 47 PM 8 -4: Graphs of Rational Functions [Day 1] 10

Example 4 Identify the following for Vertical asymptote Roots Horizontal Asymptote Roots: Holes: Y-intercept: Horizontal Asymptote look at the degrees Same Degree Divide the leading coefficients. 12/23/2021 3: 48 PM 8 -4: Graphs of Rational Functions [Day 1] 11

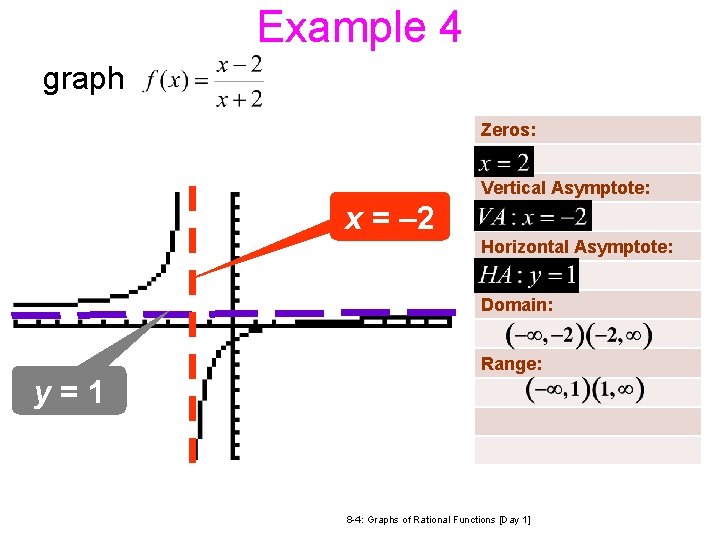
Example 4 graph Zeros: Vertical Asymptote: x = – 2 Horizontal Asymptote: Domain: Range: y=1 8 -4: Graphs of Rational Functions [Day 1]

Example 5 Identify the following for Vertical asymptote Roots Vertical asymptote Horizontal Asymptote Roots: Horizontal Asymptote look at the degrees Holes: Y-intercept: 12/23/2021 3: 48 PM 8 -4: Graphs of Rational Functions [Day 1] 13

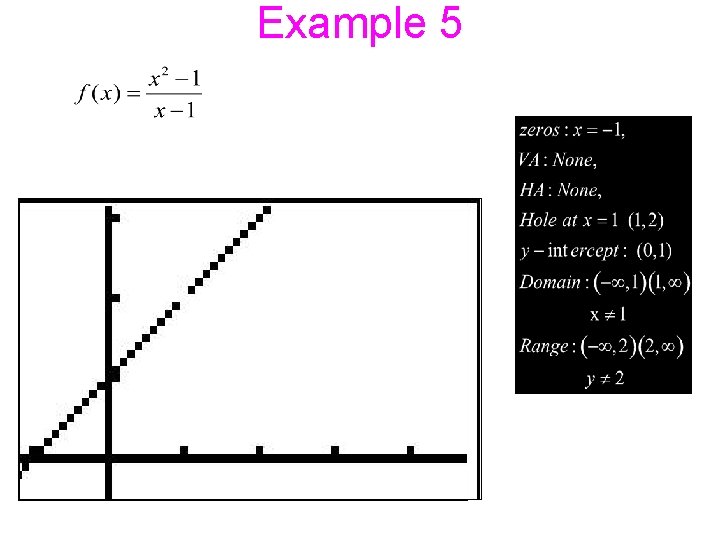
Example 5 12/23/2021 3: 48 PM 8. 4 - Graphs of Rational Functions [Day 2] 14

Example 6 Identify the following for Vertical asymptote Roots Vertical asymptote Horizontal Asymptote Roots: Horizontal Asymptote look at the degrees 12/23/2021 3: 48 PM Holes: 8 -4: Graphs of Rational Functions [Day 1] 15

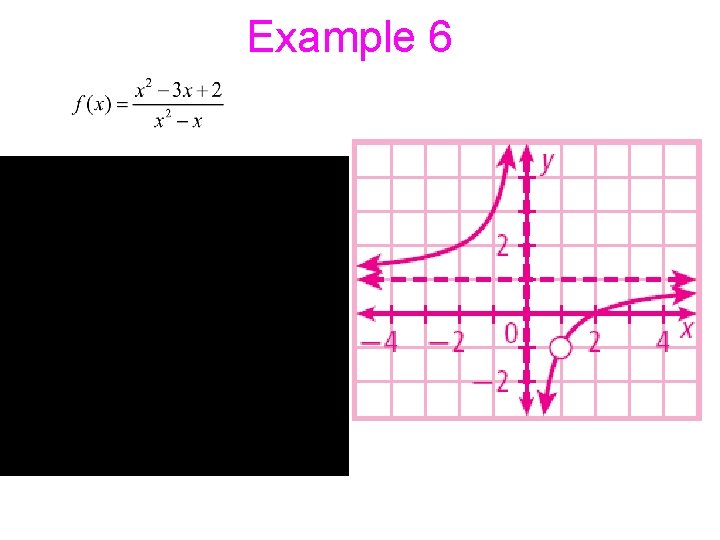
Example 6 12/23/2021 3: 48 PM 8. 4 - Graphs of Rational Functions [Day 2] 16

Extra problems following this slide

Example 7 Given, graph, determine the zeros, all asymptotes/holes, and domain 12/23/2021 3: 48 PM 8. 4 - Graphs of Rational Functions [Day 2] 18

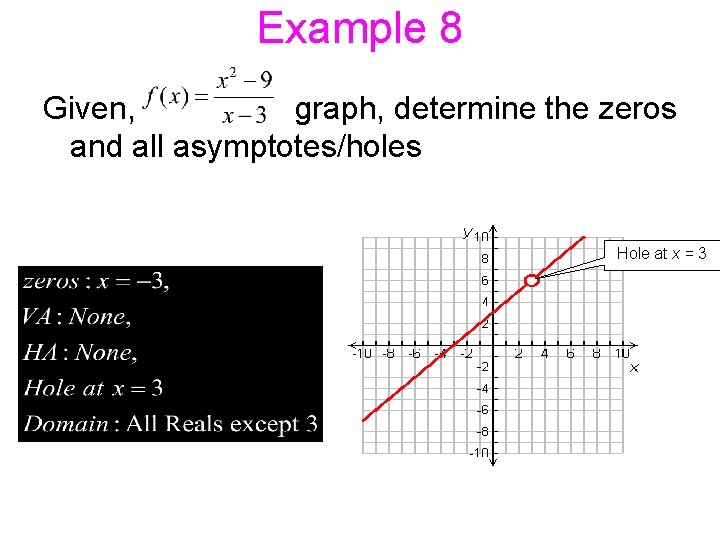
Example 8 Given, graph, determine the zeros and all asymptotes/holes Hole at x = 3 12/23/2021 3: 48 PM 8. 4 - Graphs of Rational Functions [Day 2] 19

Without a Calculator Identify the zeros and determine all of the asymptotes to the following: 4 x – 12 1. f(x) = x– 1 (x + 2)(x – 3) 2. f(x) = x +1 x – 2 3. f(x) = 2 x +x 12/23/2021 3: 48 PM 8. 4 - Graphs of Rational Functions [Day 2] 20

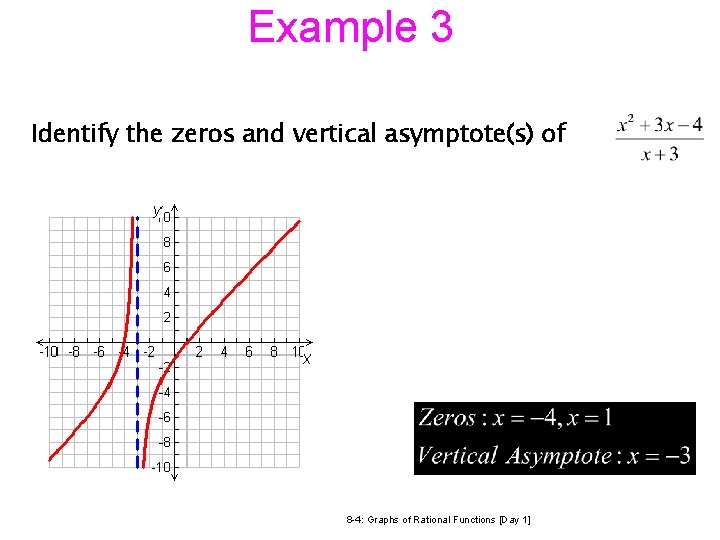
Example 3 Identify the zeros and vertical asymptote(s) of 12/23/2021 3: 48 PM 8 -4: Graphs of Rational Functions [Day 1] 21

• Horizontal Asymptotes: compare the degrees of the numerator and denominator. • Degree of Numerator > Degree of Denominator – Top bigger---NO…means NO horizontal asymptotes. Must find Oblique asymptote. • Degree of Denominator > Degree of Numerator – Bottom bigger---OH…means horizontal asymptote is y=0. Degree of Numerator = Degree of Denominator -CO…means find ratio of leading coefficients

Example 5 Identify the following for Vertical asymptote Roots Vertical asymptote Horizontal Asymptote Roots: look at the degrees Same Degree Holes: Divide the leading coefficients. 12/23/2021 3: 48 PM 8 -4: Graphs of Rational Functions [Day 1] 23

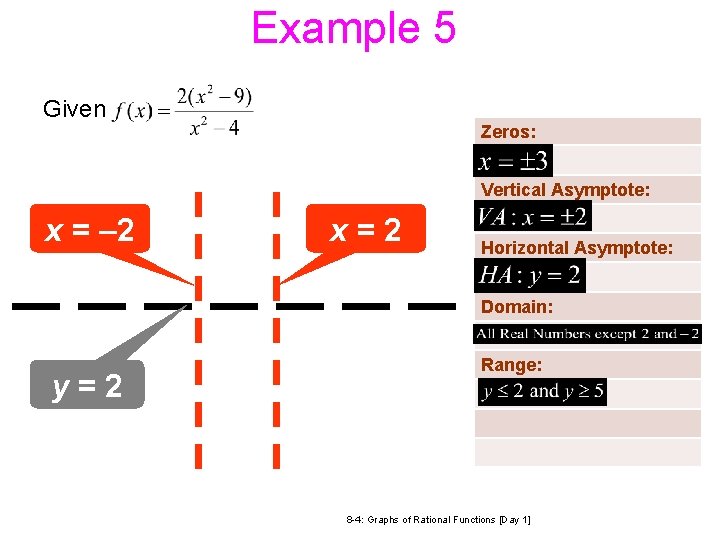
Example 5 Given Zeros: Vertical Asymptote: x = – 2 x=2 Horizontal Asymptote: Domain: Range: y=2 12/23/2021 3: 48 PM 8 -4: Graphs of Rational Functions [Day 1] 24