The Origins of Quantum Mechanics 1900 Max Planck

The Origins of Quantum Mechanics

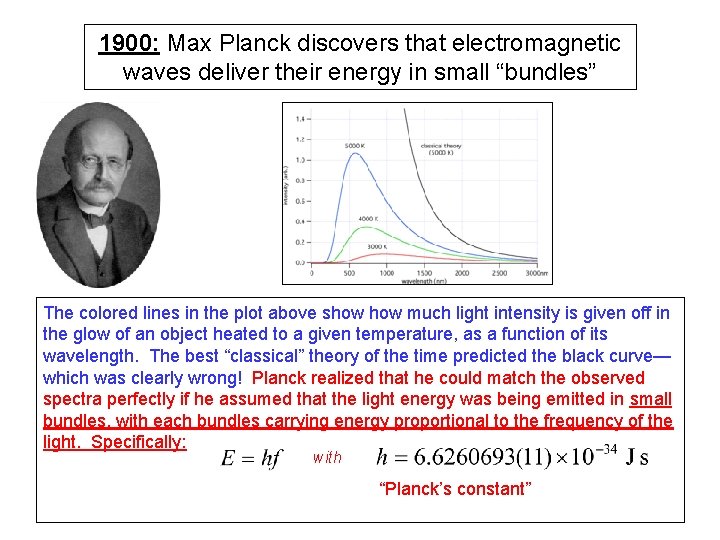
1900: Max Planck discovers that electromagnetic waves deliver their energy in small “bundles” The colored lines in the plot above show much light intensity is given off in the glow of an object heated to a given temperature, as a function of its wavelength. The best “classical” theory of the time predicted the black curve— which was clearly wrong! Planck realized that he could match the observed spectra perfectly if he assumed that the light energy was being emitted in small bundles, with each bundles carrying energy proportional to the frequency of the light. Specifically: with “Planck’s constant”

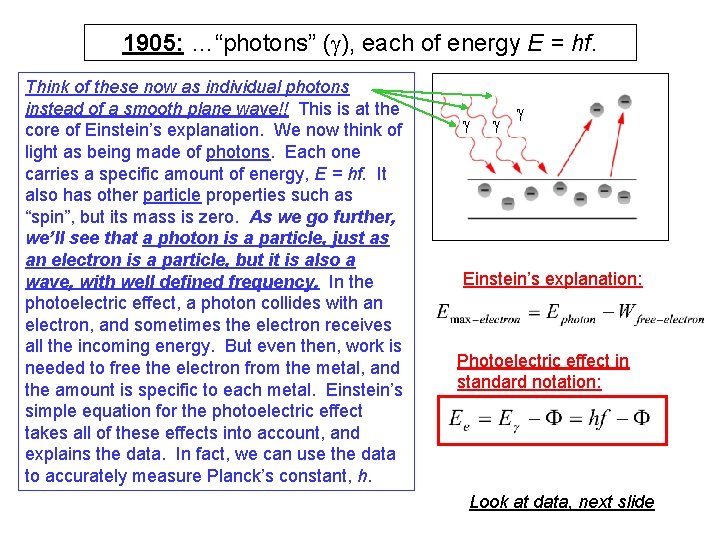
1905: Albert Einstein shows that electromagnetic waves are composed of particles, “photons” (g), each of energy E = hf. He did this by explaining the photoelectric effect, shown at right. Light of a single frequency is shined onto a metal plate, ejecting electrons from the plate. The experiment measures the rate of electrons arriving, and their maximum energy. Classical Picture At t = 0, light is shined on the plate. The E field of the electromagnetic wave causes the atomic electrons to oscillate. The oscillations build up until the electrons break way from their atoms and leave the metal. What is observed When the light is turned on, even at low intensity, electrons begin to emerge from the plate—with no time delay. Their rate depends on the light intensity, but their maximum energy depends only on the frequency of the light.

1905: …“photons” (g), each of energy E = hf. Think of these now as individual photons instead of a smooth plane wave!! This is at the core of Einstein’s explanation. We now think of light as being made of photons. Each one carries a specific amount of energy, E = hf. It also has other particle properties such as “spin”, but its mass is zero. As we go further, we’ll see that a photon is a particle, just as an electron is a particle, but it is also a wave, with well defined frequency. In the photoelectric effect, a photon collides with an electron, and sometimes the electron receives all the incoming energy. But even then, work is needed to free the electron from the metal, and the amount is specific to each metal. Einstein’s simple equation for the photoelectric effect takes all of these effects into account, and explains the data. In fact, we can use the data to accurately measure Planck’s constant, h. g g g Einstein’s explanation: Photoelectric effect in standard notation: Look at data, next slide

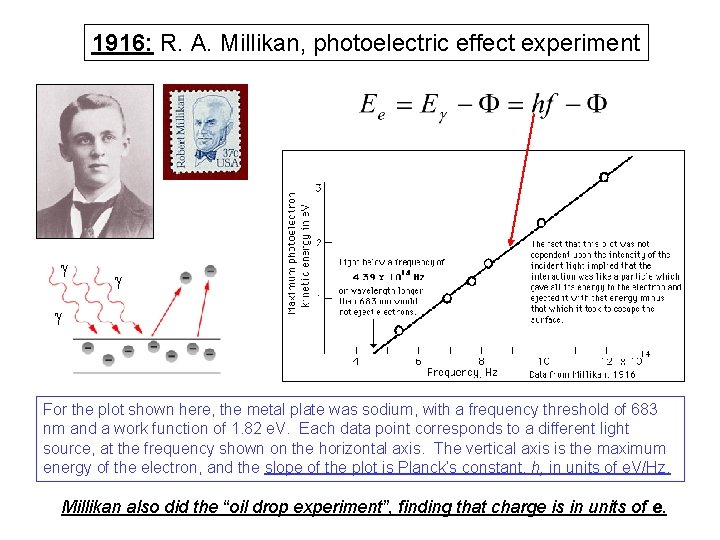
1916: R. A. Millikan, photoelectric effect experiment g g g For the plot shown here, the metal plate was sodium, with a frequency threshold of 683 nm and a work function of 1. 82 e. V. Each data point corresponds to a different light source, at the frequency shown on the horizontal axis. The vertical axis is the maximum energy of the electron, and the slope of the plot is Planck’s constant, h, in units of e. V/Hz. Millikan also did the “oil drop experiment”, finding that charge is in units of e.

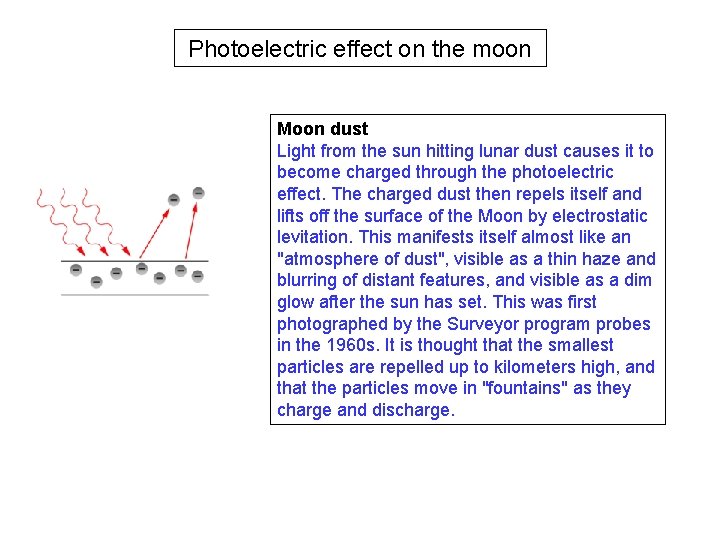
Photoelectric effect on the moon Moon dust Light from the sun hitting lunar dust causes it to become charged through the photoelectric effect. The charged dust then repels itself and lifts off the surface of the Moon by electrostatic levitation. This manifests itself almost like an "atmosphere of dust", visible as a thin haze and blurring of distant features, and visible as a dim glow after the sun has set. This was first photographed by the Surveyor program probes in the 1960 s. It is thought that the smallest particles are repelled up to kilometers high, and that the particles move in "fountains" as they charge and discharge.

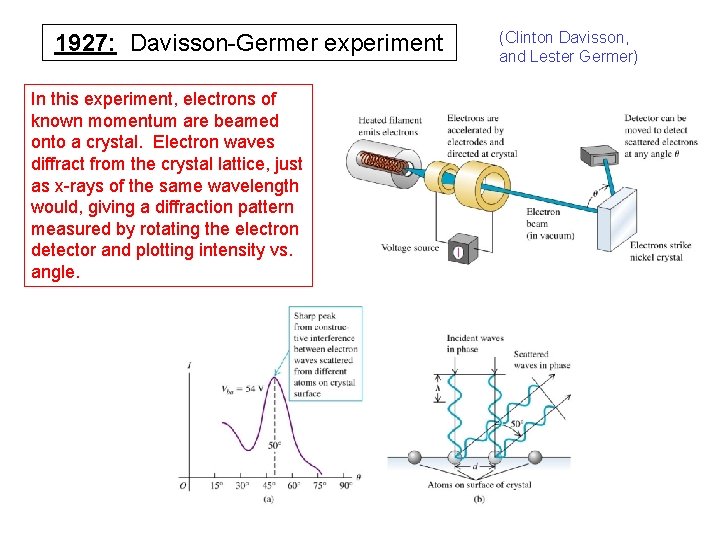
1924: Louis de Broglie puts forth the hypothesis that particles, such as the electron, are also waves of wavelength l = h/p p = h/l Notice that de Broglie put forth this idea almost 20 years after Einstein’s postulate that electromagnetic waves are photons. But we’re purposely taking this out of historical order to make it easy to understand the Bohr model of the atom (that appeared in the intervening years). De Broglie announced this idea in his Ph. D. thesis, perhaps the most spectacular Ph. D. in all of physics! (Story. ) How was the hypothesis verified? By the Davisson-Germer experiment (next slide)

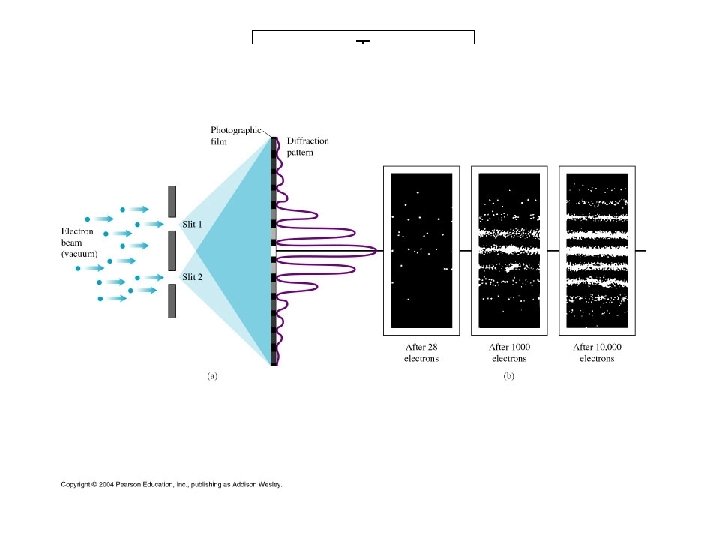
1927: Davisson-Germer experiment In this experiment, electrons of known momentum are beamed onto a crystal. Electron waves diffract from the crystal lattice, just as x-rays of the same wavelength would, giving a diffraction pattern measured by rotating the electron detector and plotting intensity vs. angle. (Clinton Davisson, and Lester Germer)

Quanta Waves are particles, and particle are waves. They are really all “one type” of object, that we call “quanta”. All quanta have energy E = hf and momentum p=h/l. What makes them differ as particles is “additional” properties: spin, mass, electric charge, weak charge, strong charge, parity, etc. (Photons are an example of a mass-less particle. ) Nature forces us to the conclusion that quanta are real, but offers no additional “guidance” to help us create a mental picture of how quanta act as both waves and particles. The best we can do currently is to label this two-sided behavior as “wave particle duality”. Quantum mechanics still fascinates and mystifies the people who work most closely with it. (Feynman quotes. )

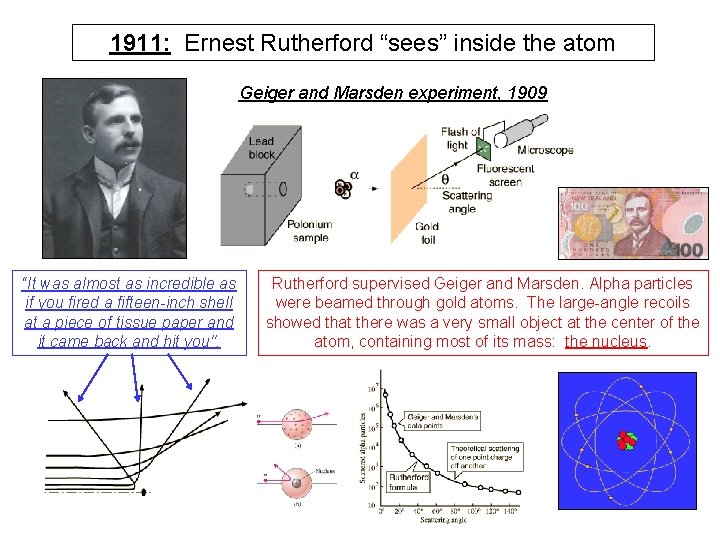
1911: Ernest Rutherford “sees” inside the atom Geiger and Marsden experiment, 1909 “It was almost as incredible as if you fired a fifteen-inch shell at a piece of tissue paper and it came back and hit you". Rutherford supervised Geiger and Marsden. Alpha particles were beamed through gold atoms. The large-angle recoils showed that there was a very small object at the center of the atom, containing most of its mass: the nucleus.

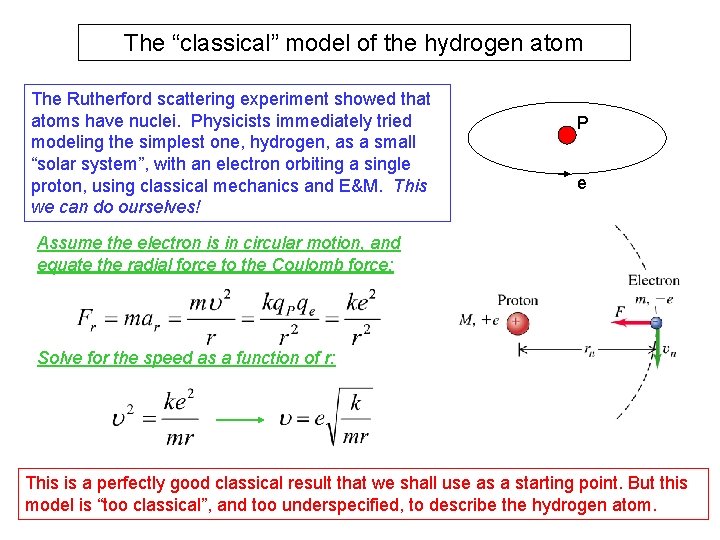
The “classical” model of the hydrogen atom The Rutherford scattering experiment showed that atoms have nuclei. Physicists immediately tried modeling the simplest one, hydrogen, as a small “solar system”, with an electron orbiting a single proton, using classical mechanics and E&M. This we can do ourselves! P e Assume the electron is in circular motion, and equate the radial force to the Coulomb force: Solve for the speed as a function of r: This is a perfectly good classical result that we shall use as a starting point. But this model is “too classical”, and too underspecified, to describe the hydrogen atom.

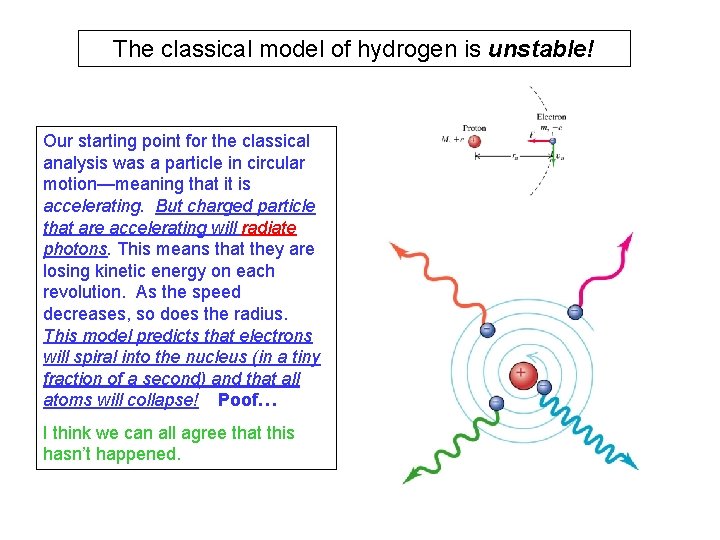
The classical model of hydrogen is unstable! Our starting point for the classical analysis was a particle in circular motion—meaning that it is accelerating. But charged particle that are accelerating will radiate photons. This means that they are losing kinetic energy on each revolution. As the speed decreases, so does the radius. This model predicts that electrons will spiral into the nucleus (in a tiny fraction of a second) and that all atoms will collapse! Poof… I think we can all agree that this hasn’t happened.

The long-standing mystery of dark lines in solar spectra The English chemist William Hyde Wollaston was in 1802 the first person to note the appearance of a number of dark features in the solar spectrum. In 1814, Fraunhofer independently rediscovered the lines and began a systematic study and careful measurement of the wavelength of these features. In all, he mapped over 570 lines, and designated the principal features with the letters A through K, and weaker lines with other letters. It was later discovered by Kirchoff and Bunsen that each chemical element was associated with a set of spectral lines, and deduced that the dark lines in the solar spectrum were caused by absorption by those elements in the upper layers of the sun. Some of the observed features are also caused by absorption in oxygen molecules in the Earth's atmosphere.

1915: Niels Bohr “figures out” the hydrogen atom, and “explains” absorption and emission lines Bohr started from the classical model, but then added what was known from solar spectrum lines: (1) all hydrogen atoms must be identical, and (2) they absorb and emit light only at specific frequencies (corresponding to specific energies, Eg = hf). His major insight was that different electron orbits correspond to different electron total energy. The atom would emit and absorb at specific frequencies if (1) orbits would be “allowed” only at certain radii, (2) photons were emitted or absorbed when electrons “jump” from one orbit to another. An electron jumping from large radius to small would emit a photon of energy equal to the energy difference between orbits. Absorption is the inverse process.

1915: Niels Bohr “figures out” the hydrogen atom, but we’ll calculate it as de Broglie would. Bohr fished around and found that, by restricting the angular momentum of the orbits to certain values, he could reproduce the hydrogen spectrum. But we are going to start out with de Broglie’s equation for momentum, because it is easy to see why only certain orbits are allowed. In de Broglie’s picture, we should treat the electrons as particle waves traveling in a circle around the nucleus. Each orbit, these waves return on themselves, and if they are not in phase, they will destructively interfere. Constructive in interference will occur only when the waves are in phase after one revolution. This means for an orbit of a given radius, an integral number of wavelengths must fit into one circumference: n = 1, 2, 3, …

Solving for the Bohr orbits of hydrogen Standing waves of the electron in circular orbit: n = 1, 2, 3, … Classical circular orbits of the electron in the Coulomb field of the proton Take the two formulas above, square the velocity, and equate: “Bohr radii” of hydrogen, n = 1, 2, 3 … Bohr radius of the “ground state” of hydrogen (n = 1): o Insert the Bohr radii, rn, into the first equation for v: “Bohr velocities” of hydrogen, n = 1, 2, 3 … (Note how the Bohr radii and velocities change with n. )

The emission and absorption spectrum of hydrogen Light is emitted when an electron jumps from an orbit of large radius to a smaller one. It is absorbed in jumps from a small radius to a larger one. The photon energy equals the magnitude of the electron energy difference before and after the jump, which in turn sets the photon wavelength. The pattern of wavelengths for hydrogen was measured in the early 1800’s, and is summarized by the formula at the right, found by Rydberg in the 1890’s. (Also Balmer. ) With n > m: m=1: Lyman series (ultraviolet) m=2: Balmer series (visible) m=3: Paschen series (infrared)

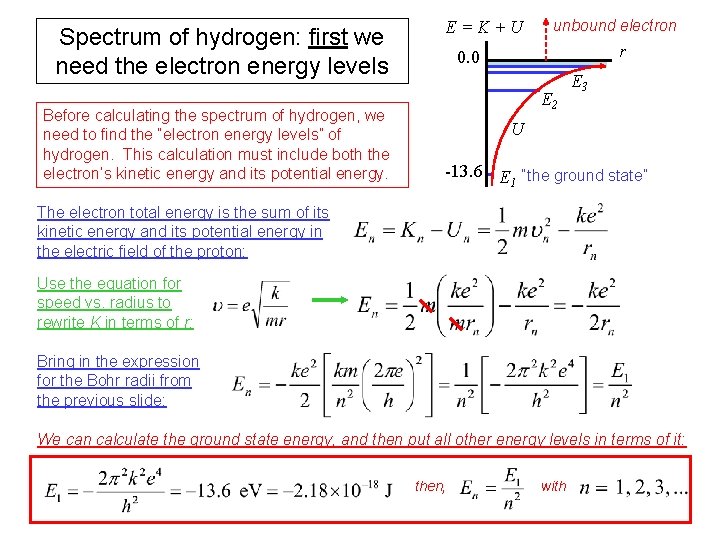
Spectrum of hydrogen: first we need the electron energy levels Before calculating the spectrum of hydrogen, we need to find the “electron energy levels” of hydrogen. This calculation must include both the electron’s kinetic energy and its potential energy. E = K + U unbound electron r 0. 0 E 2 E 3 U -13. 6 E “the ground state” 1 The electron total energy is the sum of its kinetic energy and its potential energy in the electric field of the proton: Use the equation for speed vs. radius to rewrite K in terms of r: Bring in the expression for the Bohr radii from the previous slide: We can calculate the ground state energy, and then put all other energy levels in terms of it: then, with

Now to derive the spectrum of hydrogen Light is emitted or absorbed when an electron jumps from one Bohr orbit to another. The energy of the photon equals the difference in electron total energy between the two orbits: Bring in the electron energy levels from the previous slide: then, with So that: Solving for the wavelength and putting in the numbers, we match the experimental result! It is amazing, and somewhat lucky, that Bohr’s model—containing a mixture of classical and quantum ideas—actually got the right result! But it gave people the courage to press forward with a more fundamental description (2 slides away).

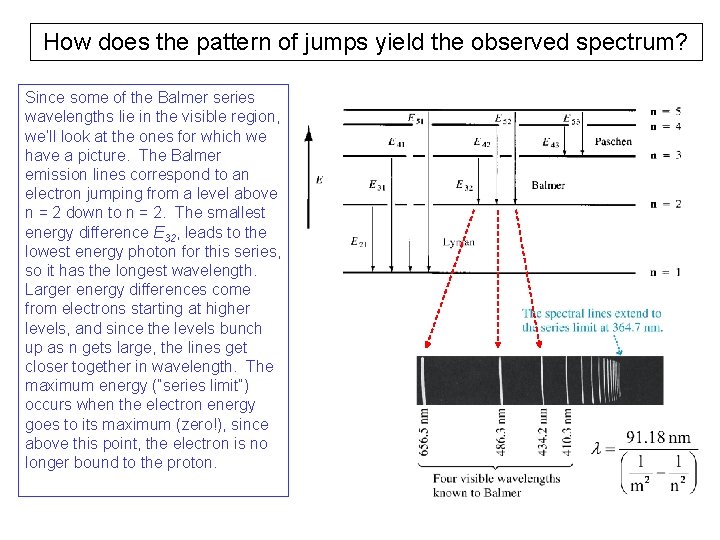
How does the pattern of jumps yield the observed spectrum? Since some of the Balmer series wavelengths lie in the visible region, we’ll look at the ones for which we have a picture. The Balmer emission lines correspond to an electron jumping from a level above n = 2 down to n = 2. The smallest energy difference E 32, leads to the lowest energy photon for this series, so it has the longest wavelength. Larger energy differences come from electrons starting at higher levels, and since the levels bunch up as n gets large, the lines get closer together in wavelength. The maximum energy (“series limit”) occurs when the electron energy goes to its maximum (zero!), since above this point, the electron is no longer bound to the proton.

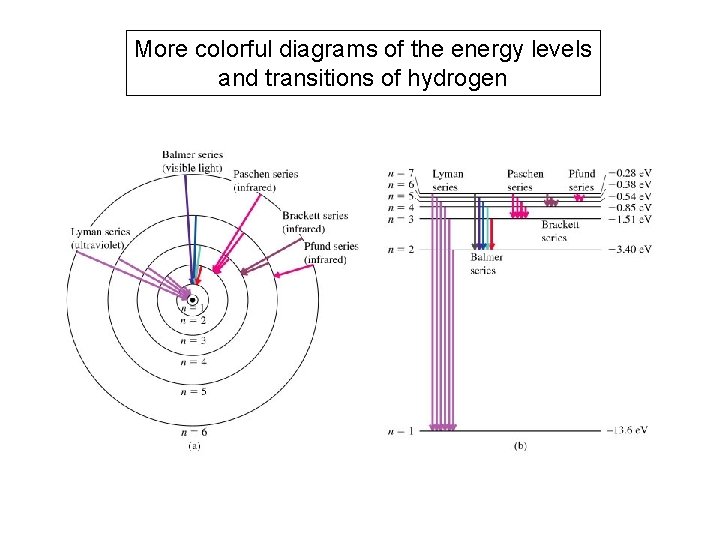
More colorful diagrams of the energy levels and transitions of hydrogen

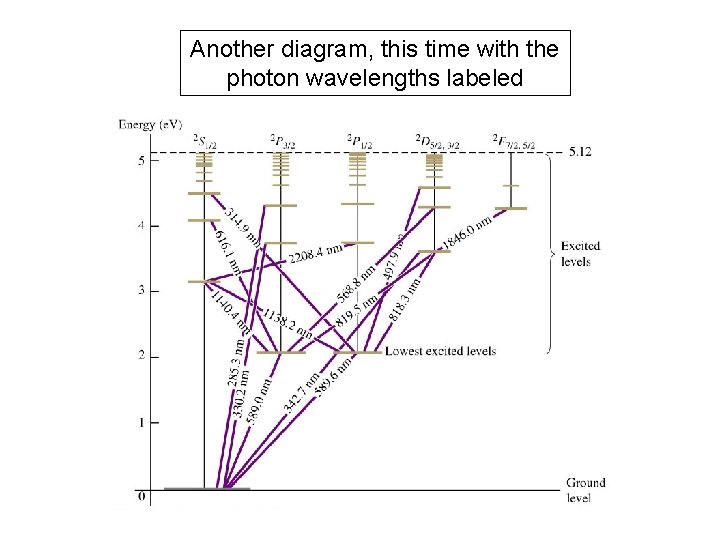
Another diagram, this time with the photon wavelengths labeled

1926: Max Born figures out how to interpret quantum waves. Max Born (1882 - 1970) was a German mathematician and physicist. He won the 1954 Nobel Prize in Physics, and was also the maternal grandfather of the British-born Australian singer and actress Olivia Newton-John. The picture above is an example of a particle “wave packet” or “wave function”. It has a length—the region where we might find the particle—and a wavelength that determines its momentum (from the de Broglie equation). In general, wave functions can be complex, with imaginary parts. The plot above is of the real part only, and there is some imaginary part which might look similar, but offset in phase. Max Born realized that if one takes the “square” of the wave function, in the complex sense, what results is a probability density, telling where the particle might be found, and with what probability: Notice how similar this procedure is to squaring a wave amplitude to find the intensity of the wave. In this case, the amplitude has no reasonable “meaning” until it is squared. This mathematical procedure always yields a positive probability density, which is essential!

1926: Erwin Schrodinger figures out the wave equation for particles, using the probabilistic wave function of Max Born Erwin Schrödinger (1887 -1961) was an Austrian physicist who achieved fame for his contributions to quantum mechanics, especially the Schrödinger equation, for which he received the Nobel Prize in 1933. In 1935, he proposed the Schrödinger's cat thought experiment. To cut down on so many factors of 2 p: Schrodinger started with conservation of energy: He created an operator equation, where space and time derivatives act on the wave function. The left hand side has units of E = hf, and the first term on the right has units of (p = h/l) squared. This is the one dimensional version: 3 D version adds y and z derivatives. One can now describe quantum waves traveling or standing in 3 D: When this is applied to the hydrogen atom—by making V the Coulomb potential energy—the result is standing waves in 3 D, the “orbitals” of hydrogen.

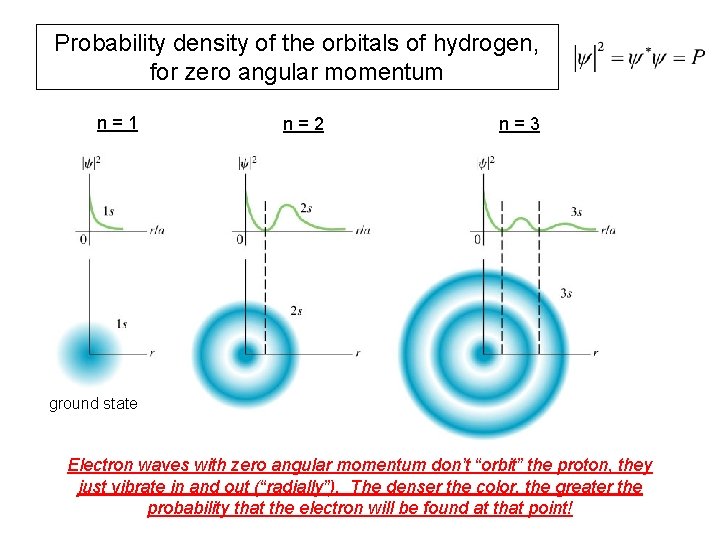
Probability density of the orbitals of hydrogen, for zero angular momentum n=1 n=2 n=3 ground state Electron waves with zero angular momentum don’t “orbit” the proton, they just vibrate in and out (“radially”). The denser the color, the greater the probability that the electron will be found at that point!

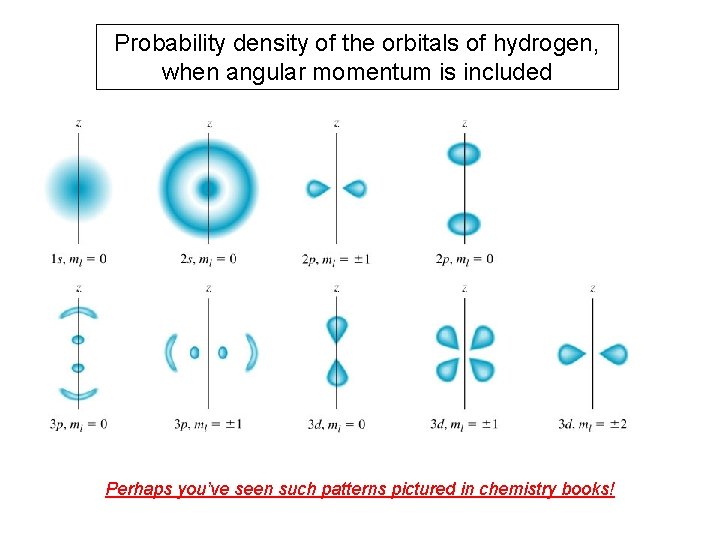
Probability density of the orbitals of hydrogen, when angular momentum is included Perhaps you’ve seen such patterns pictured in chemistry books!

Notice how the wave-particle duality has been dealt with mathematically (1) The wave function, Y, is a smooth wave (not “grainy”), with real and imaginary parts that may oscillate just like any classical wave. (2) Wave functions propagate according to Huygen’s principle, and they may be superposed to give all the interference and diffraction effects we have studied in optics. So they can describe the intensity patterns of photons, electrons, and other particles. As we’ve seen, quantum waves may be traveling, or standing. (3) To find out where a given particle might be, we square the wave function to find the probability density. Until we interact with it, and measure its location, it could be anywhere that this density is non-zero.

Solvay Conference, 1927 A. Piccard, E. Henriot, P. Ehrenfest, Ed. Herzen, Th. De Donder, E. Schrödinger, E. Verschaffelt, W. Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin, P. Debye, M. Knudsen, W. L. Bragg, H. A. Kramers, P. A. M. Dirac, A. H. Compton, L. de Broglie, M. Born, N. Bohr, I. Langmuir, M. Planck, M. Curie, H. A. Lorentz, A. Einstein, P. Langevin, Ch. E. Guye, C. T. R. Wilson, O. W. Richardson

A footnote on quantum mechanics… Einstein could never accept some of the revolutionary ideas of quantum mechanics ("God does not play dice"). When reminded in 1927 that he revolutionized science 20 years earlier, Einstein replied, "A good joke should not be repeated too often. "

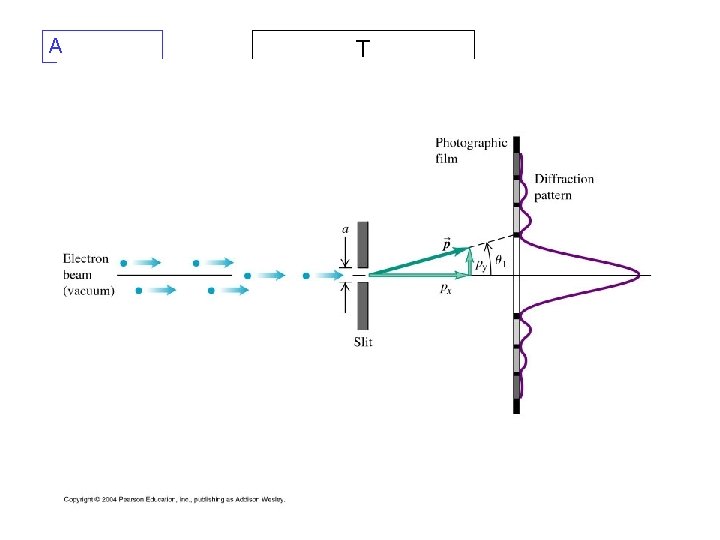
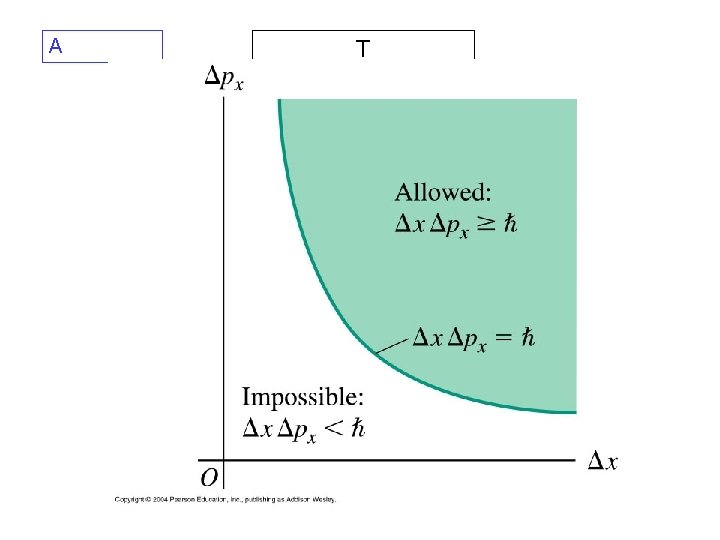
A T

A T

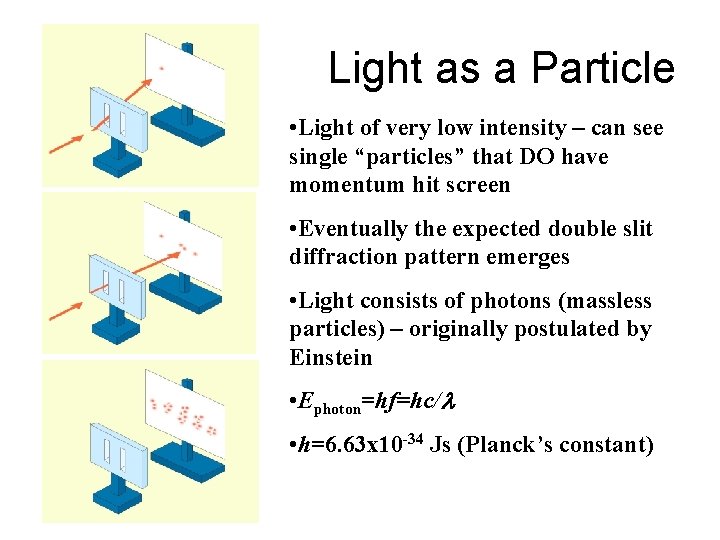
Light as a Particle • Light of very low intensity – can see single “particles” that DO have momentum hit screen • Eventually the expected double slit diffraction pattern emerges • Light consists of photons (massless particles) – originally postulated by Einstein • Ephoton=hf=hc/l • h=6. 63 x 10 -34 Js (Planck’s constant)

T

Matter as a Wave • Originally postulated by de Broglie in 1924 – NO evidence at this point – He surmised that l=h/p: E=1/2 mv 2=p 2/2 m • Davison-Germer (1924) – Electron diffraction – Found by accident (“faulty” nickel target) – “ruined” Germer’s second honeymoon • G. P. Thompson – Went through the crystal

Particle Waves ln=2 L/n Since l=h/mv, vn=nv 1 v 1=h/(2 Lm) En=½mvn 2 En=n 2 E 1 E 1=h 2/(8 m. L 2) Me: l=10 -34 m, E 1=10 -38 J, n=1035 (n BIG, classical) Electrons not!!!

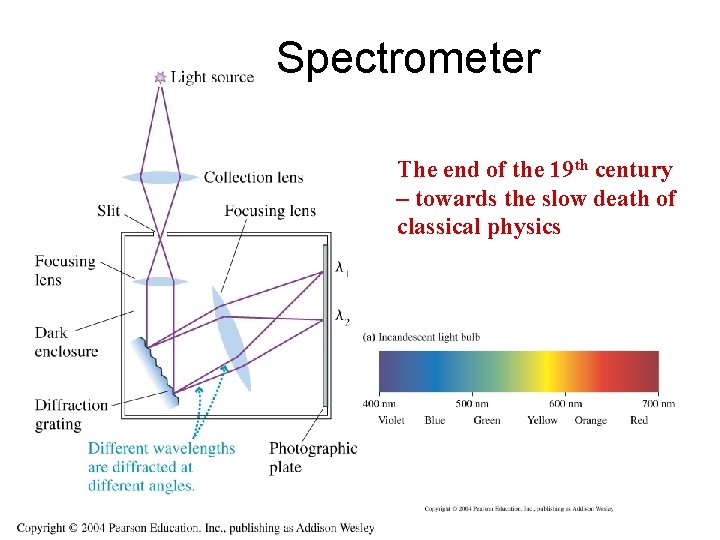
Spectrometer The end of the 19 th century – towards the slow death of classical physics