The OrbitStabilizer Theorem Stabilizers n n Let G

The Orbit-Stabilizer Theorem

Stabilizers n n Let G be a group of permutations on a set S. For each i in S, let stab. G(i) be the set of permutations π in G that fix i. That is, stab. G(i) = {π in G | π(i) = i}

Visual Stabilizers n n Think of D 4 as a group of permutations acting on a square region, S. Let p be the point in S indicated by the red dot. p S n Find stab (p) D 4

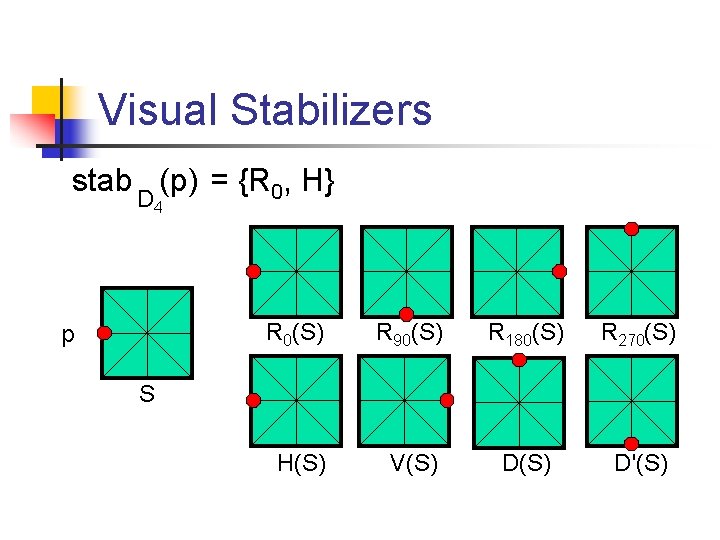
Visual Stabilizers stab (p) = {R 0, H} D 4 p R 0(S) R 90(S) R 180(S) R 270(S) H(S) V(S) D'(S) S

Visual Stabilizers stab (p) = {R 0, D} D 4 p R 0(S) R 90(S) R 180(S) R 270(S) H(S) V(S) D'(S) S

More Stabilizers n n n Let G be the group of permutations: = (1) π2 = (124) π3 = (142) π4 = (35) π5 = (124)(35) π6 = (142)(35) stab. G(1) = { , π4} stab. G(3) = { , π2, π3}

stab. G(a) is a subgroup of G. n Proof: Let us use the two-step test. (a) = a, so stab. G(a) is not empty. Choose any in stab. G(a). Then (a) = (a) since in stab. G(a). =a since in stab. G(a). So stab. G(a) is closed. Since (a) = a, -1(a) = a, so stab. G(a) is closed under inverses. By the two-step test, stab. G(a) ≤ G.

Orbits n n Let G be a group of permutations on a set S. For each s in S, the orbit of s under G, denoted orb. G(s) = {π(s) | π in G}

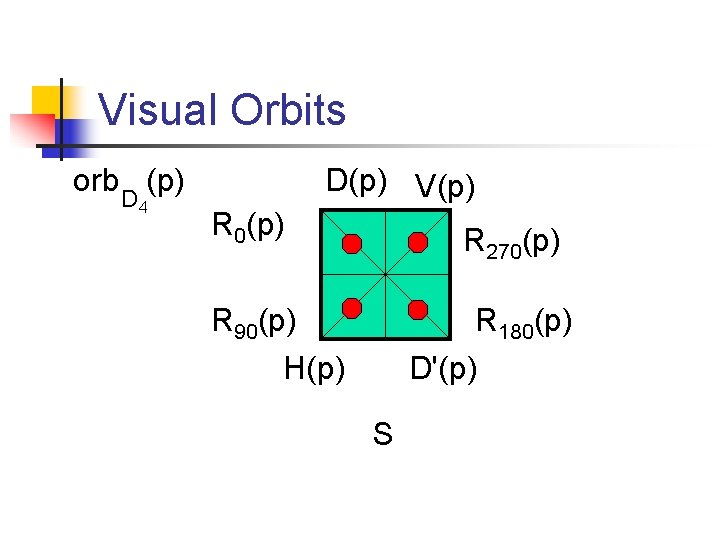
Visual Orbits orb (p) D 4 D(p) V(p) R 0(p) R 270(p) R 90(p) H(p) R 180(p) D'(p) S

More Orbits n n n Let G be the group of permutations: = (1) π2 = (124) π3 = (142) π4 = (35) π5 = (124)(35) π6 = (142)(35) stab. G(1) = { , π4} orb. G(1) = {1, 2, 4} stab. G(3) = { , π2, π3} orb. G(3) = {3, 5}

Orbit-Stabilizer Theorem n n Let G be a finite group of permutations on a set S. Then for any i in S, |G| =|orb. G(i)| |stab. G(i)| Proof: We will show there is a one-to-one correspondence between orb. G(i) and the cosets of stab. G(i). Then |orb. G(i)| = |G: stab. G(i)|. But |G| = |G: stab. G(i)| |stab. G(i)| by Lagrange, and the result follows.

The correspondence n Let H = stab. G(i), and choose any permutation π in H. The correspondence between orb. G(i) and the cosets of stab. G(i) is given by where (π(i)) = πH. In case there is another permutation with (i) = π(i), we need to show is really a function, that is, that (π(i)) = ( (i)).

Show is one-to-one and onto n n But if π(i) = (i), then -1π(i) = i so -1π is in stab. G(i) = H. Hence πH = H So (π(i)) = ( (i)) as required. To show is one-to-one, reverse the steps. Clearly is onto. This completes the proof.