The optimal path to turbulence in shear flows

The optimal path to turbulence in shear flows Dan Henningson Collaborators: Antonios Monokrousos, Luca Brandt, Alex Bottaro, Andrea Di Vita Monokrousos et al. PRL 106, 134502, 2011

Outline • Transition scenarios and threshold amplitudes for subcritical transition - How low amplitude can a disturbance have and still cause transition to turbulence? Mechanisms? • Optimal control theory applied to transition optimization - Objective function from thermodynamic considerations • Results for transition optimization in plane Couette flow - Analysis of non-linear optimal disturbance evolution • Conclusions

Transition thresholds and basin of attraction • Lundbladh, Kreiss, Henningson JFM 1994 - Transition thresholds in plane Couette flow, incl NL bound • Reddy, Schmid, Bagget, Henningson JFM 1998 - Transition thresholds for streaks and oblique waves in channel flows • Bottin and H. Chaté EPJB 1998 - Statistical analysis of the transition to turbulence in plane Couette flow • Hof, Juel, Mullin PRL 2002 - Scaling of the Turbulence Transition Threshold in a Pipe • Faisst, Eckhardt JFM 2004; Lebovitz NL 2009 - Complex boundary of basin of attraction – varying lifetimes • Viswanath & Cvitanovic JFM 2009 - Low amplitude disturbances evolving into lower branch travelling waves • Duguet, Brandt, Larsson PRE 2010 - Optimal perturbations combination of linear optimal modes • Pringle, Kerswell PRL 2011 - Non-linear optimal disturbance (optimization not including transition)

Shear flow transition scenarios, BL example Non-modal instability Modal instability Subcritical bypass transition Classical supercritical transition Low disturbance levels High disturbance levels Consider small periodic box as model problem Simulations performed by Philipp Schlatter

Bypass transition: 2 main scenarios Streak breakdown Oblique transition streak/vortex oblique mode fundamental mode induced streak fundamental mode

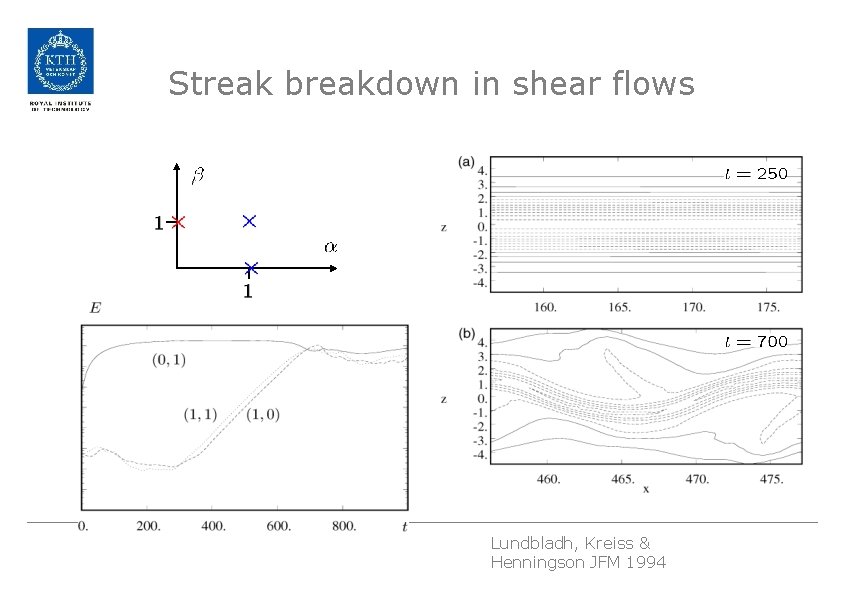
Streak breakdown in shear flows Lundbladh, Kreiss & Henningson JFM 1994

Oblique transition in shear flows Schmid & Henningson PF 1992 streaks are triggered by a pair of oblique waves

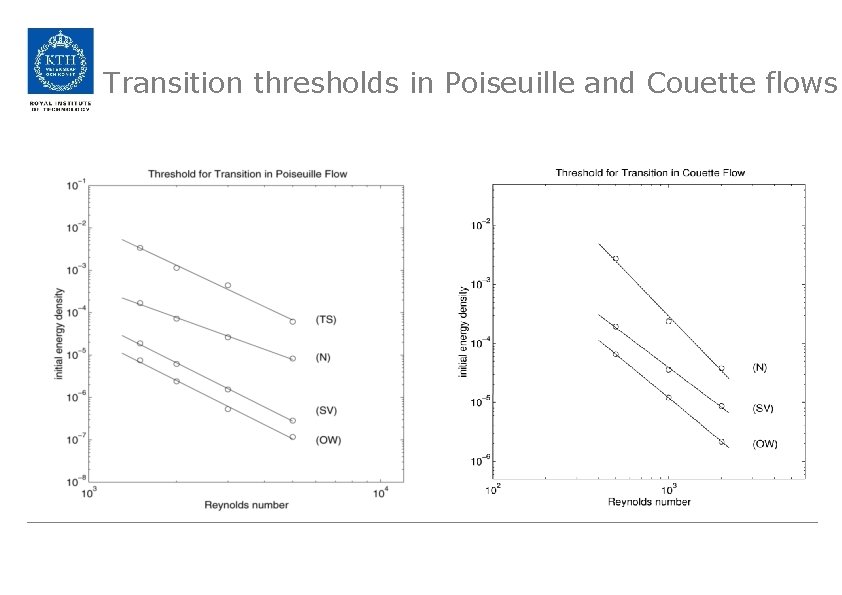
Transition thresholds in Poiseuille and Couette flows

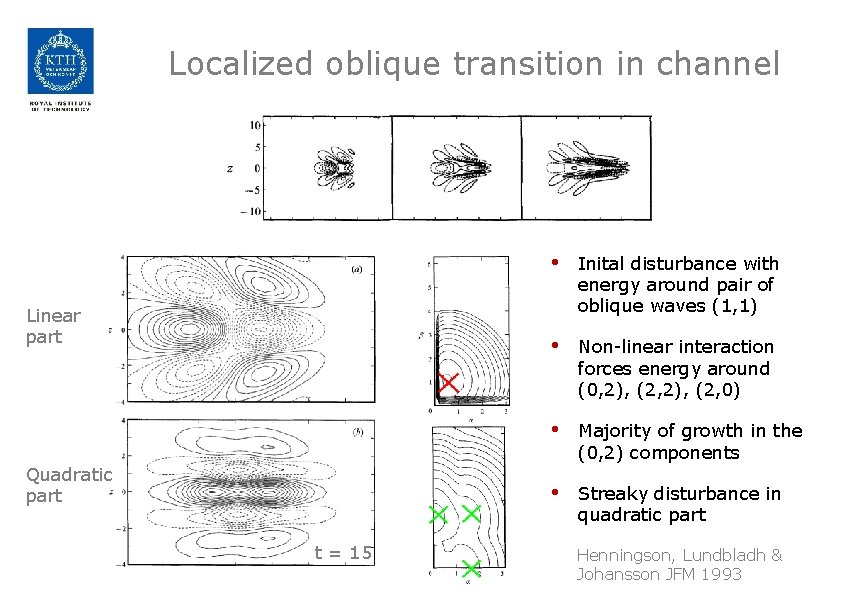
Localized oblique transition in channel Linear part Quadratic part t = 15 • Inital disturbance with energy around pair of oblique waves (1, 1) • Non-linear interaction forces energy around (0, 2), (2, 0) • Majority of growth in the (0, 2) components • Streaky disturbance in quadratic part Henningson, Lundbladh & Johansson JFM 1993

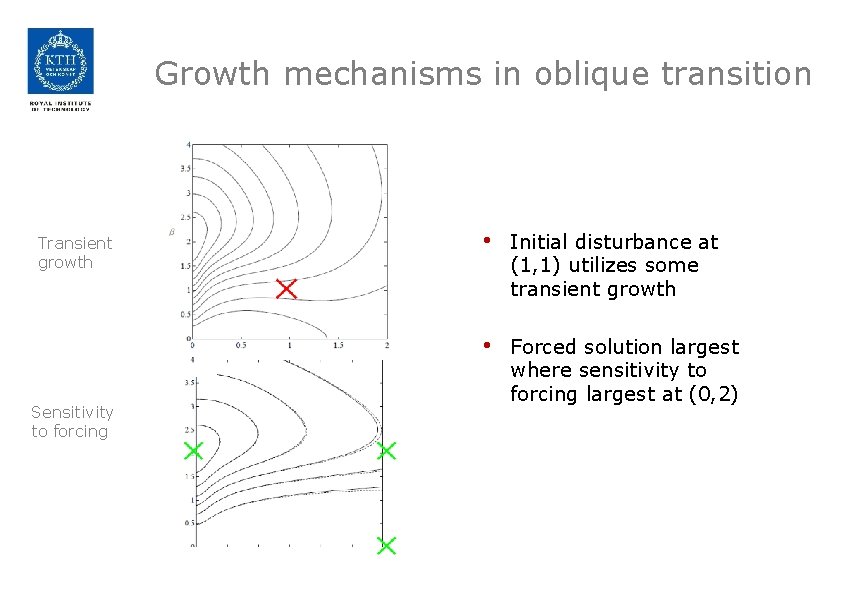
Growth mechanisms in oblique transition Transient growth Sensitivity to forcing • Initial disturbance at (1, 1) utilizes some transient growth • Forced solution largest where sensitivity to forcing largest at (0, 2)

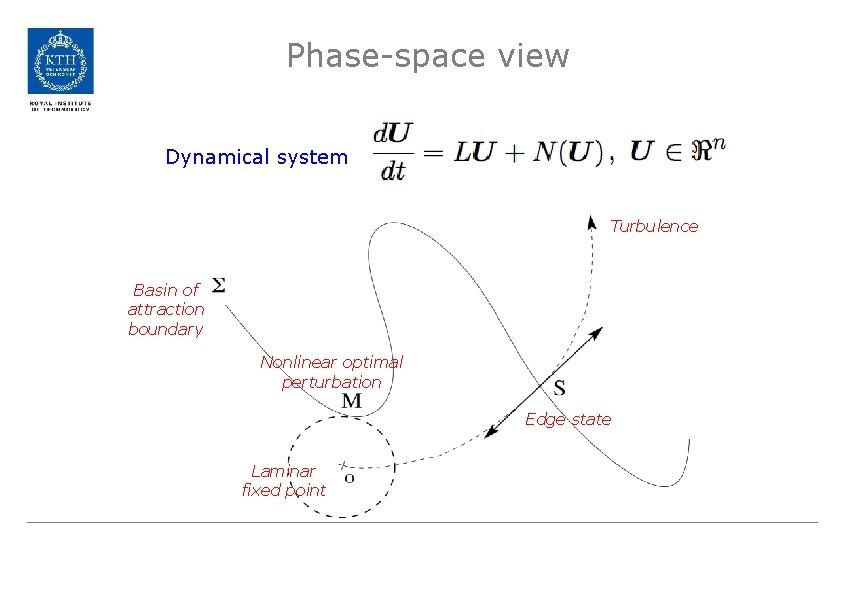
Phase-space view Dynamical system Turbulence Basin of attraction boundary Nonlinear optimal perturbation Edge state Laminar fixed point

Non-linear optimal disturbances • Searching for the optimal path to transition - Initial disturbances with minimum energy • Objective function: time average including turbulent flow - Disturbance kinetic energy - Viscous dissipation • Flow: Plane Couette

Objective function from Malkus principle • Malkus 1956 - Outline of a theory of turbulent shear flow Malkus heuristic principle: A viscous turbulent incompressible Channel flow in statistically steady state maximizes viscous dissipation • Glansdorff, Prigogine 1964 - On a general evolution criterion in macroscopic physics Di Vita (2010) derived a general criterion for stability in several diverse physical systems far from equilibrium in a statistically steady state, used by to show Malkus principle

Optimization using a Lagrange multiplier technique – Lagrange Function: • Find extrema of functional Constraint under specific constrains

Optimal initial condition Looking for the initial condition that maximizes the time integral of viscous dissipation Governing equations and objective function Lagrange functional • and : Lagrange multipliers • : very small initial amplitude as close as possible to the laminar – turbulent boundary

Optimal initial condition – Variations of the Lagrange function with respect to each variable – Set each term to zero independently • Standard non-linear Navier-Stokes • Adjoint Navier-Stokes (retrieved using integration by parts) • Normalization condition

Optimal initial condition-Boundary terms – Integration by parts give • Spatial boundary terms – We choose boundary conditions for the adjoint system so that all the terms cancel out, implying same periodic and Dirichlet BC as forward problem. • Temporal boundary terms give the initial conditions for the adjoint and forward problem

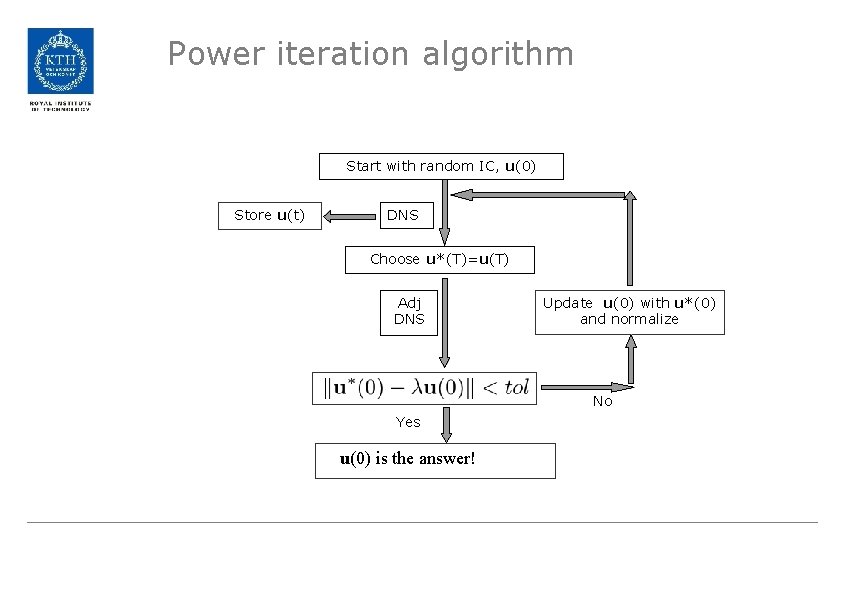
Power iteration algorithm Start with random IC, u(0) Store u(t) DNS Choose u*(T)=u(T) Adj DNS Update u(0) with u*(0) and normalize No Yes u(0) is the answer!

Numerical Code – Fully-Spectral numerical code • Fourier series in the wall-parallel directions • Chebyshev polynomials – MPI parallelization with capabilities more than 104 processors • Open-MP support for smaller scale simulations – Capabilities: • Couette, Plane channel, boundary layers with and without acceleration, sweep, etc. • Suitable for both fully turbulent flows as well as a accurate stability analysis of laminar flows • DNS & LES

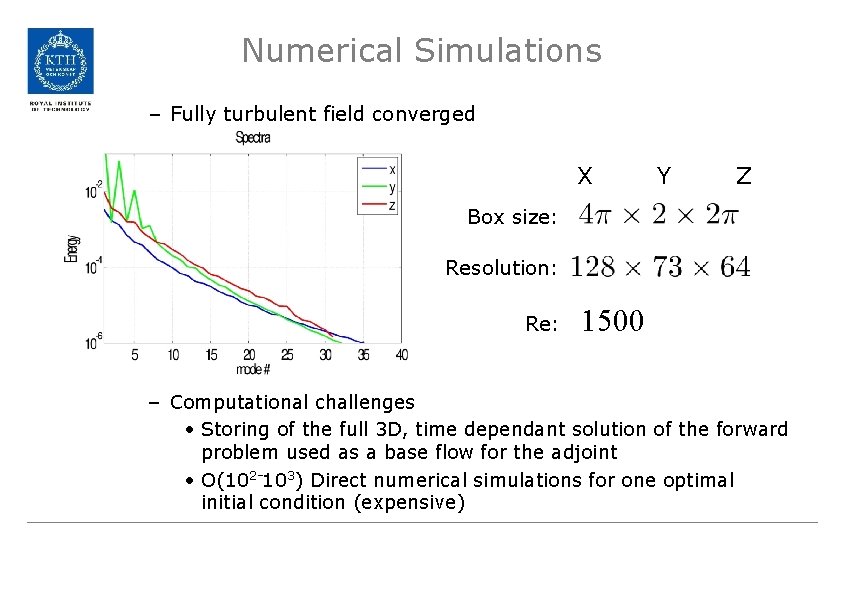
Numerical Simulations – Fully turbulent field converged X Y Z Box size: Resolution: Re: 1500 – Computational challenges • Storing of the full 3 D, time dependant solution of the forward problem used as a base flow for the adjoint • O(102 -103) Direct numerical simulations for one optimal initial condition (expensive)

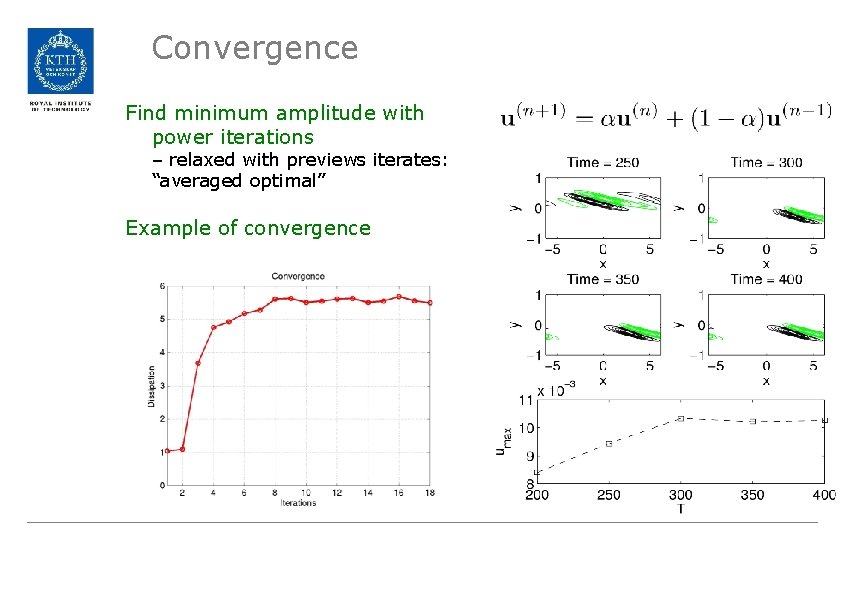
Convergence Find minimum amplitude with power iterations – relaxed with previews iterates: “averaged optimal” Example of convergence

Optimizing for the amplitude • Start with high optimization amplitude run until convergence • Compute transition threshold for optimized disturbance using bisection algorithm lowers amplitude (green circles) • Reduce amplitude and repeat until flow always re-laminarizes. • Lowest amplitude where transition occur is optimal initial condition (red star) • Fastest path to transition is the optimal path for lowest initial amplitude The red star is the optimal! The blue squares correspond to optimisation around the laminar flow (Pringle & Kerswell) • Transition thresholds for lower optimization amplitudes are higher than optimal initial condition (blue squares)

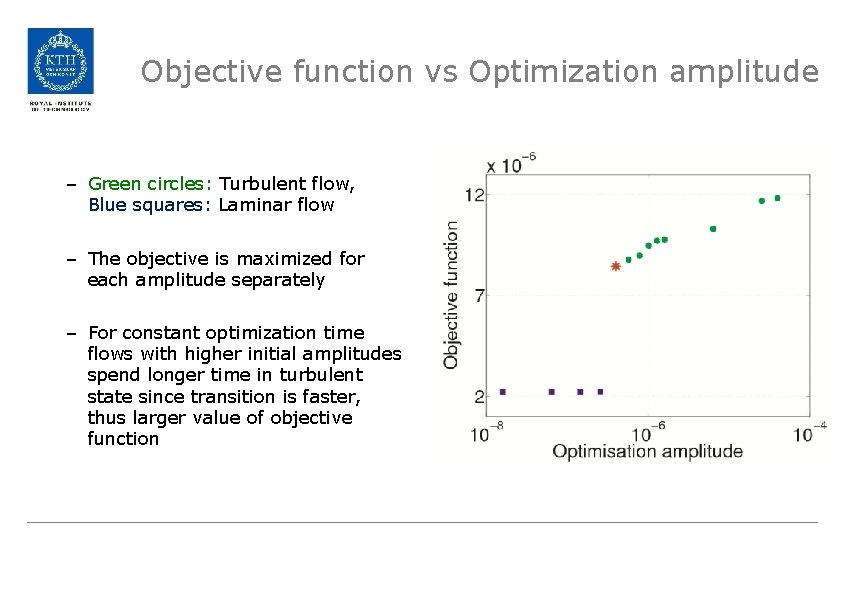
Objective function vs Optimization amplitude – Green circles: Turbulent flow, Blue squares: Laminar flow – The objective is maximized for each amplitude separately – For constant optimization time flows with higher initial amplitudes spend longer time in turbulent state since transition is faster, thus larger value of objective function

Optimal initial condition localized • Total initial energy of disturbance constant during optimization • Local amplitude can be higher for same total energy if initial condition is localized • Transition caused by large local non-linear interactions

Optimal path to turbulence: different Reynolds numbers • Convergence at lower Re more difficult – longer time to transition – timescale larger for reaching statistically steady state • Convergence at larger Re more difficult – higher resolution required • Optimal path close to edge trajectories – steady for lower Re – chaotic for higher Re

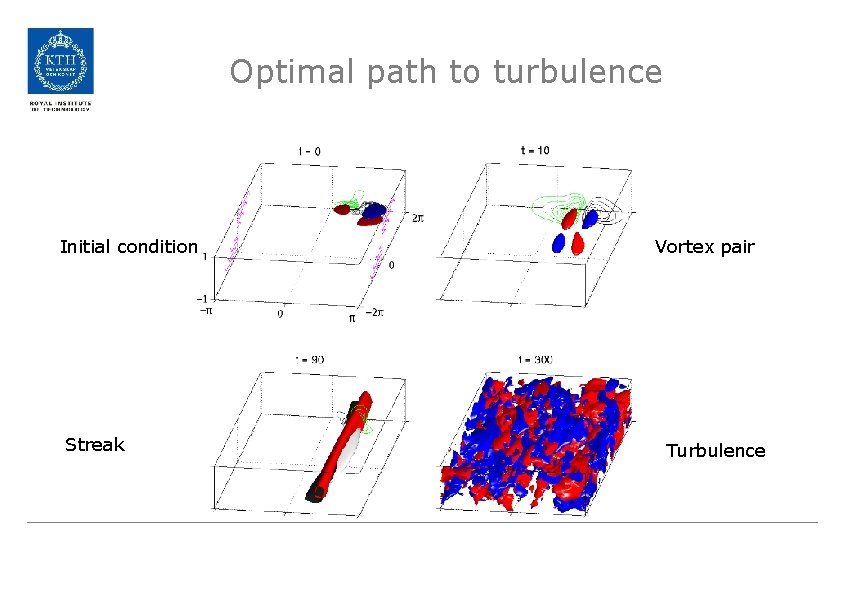
Optimal path to turbulence Initial condition Streak Vortex pair Turbulence

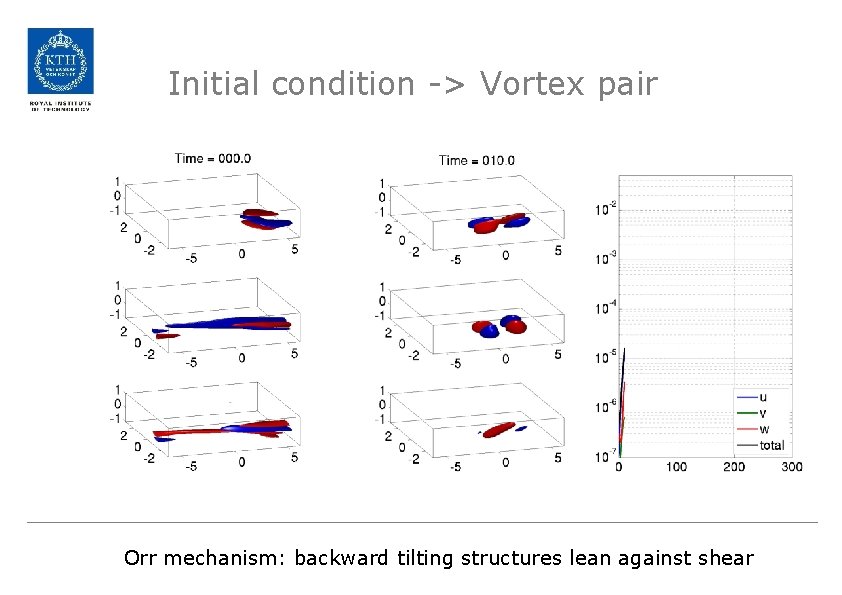
Initial condition -> Vortex pair Orr mechanism: backward tilting structures lean against shear

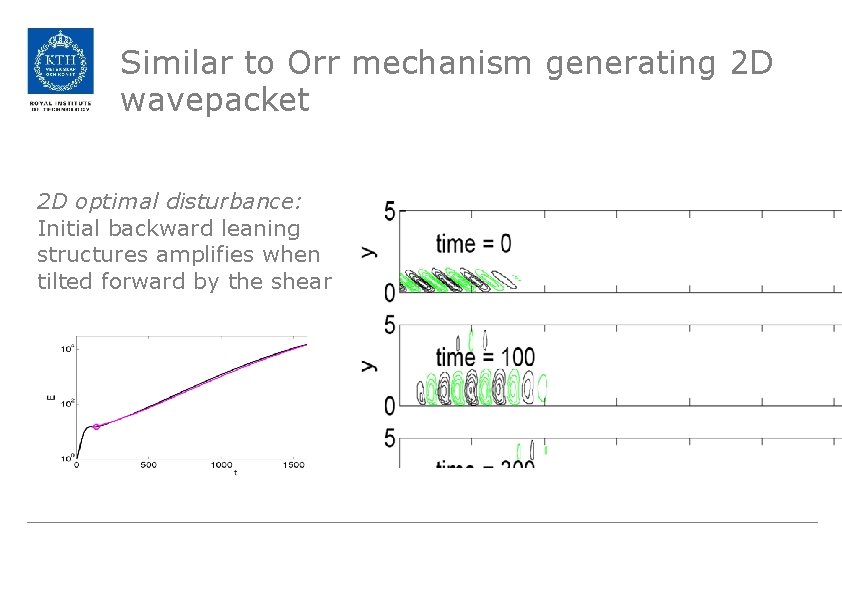
Similar to Orr mechanism generating 2 D wavepacket 2 D optimal disturbance: Initial backward leaning structures amplifies when tilted forward by the shear

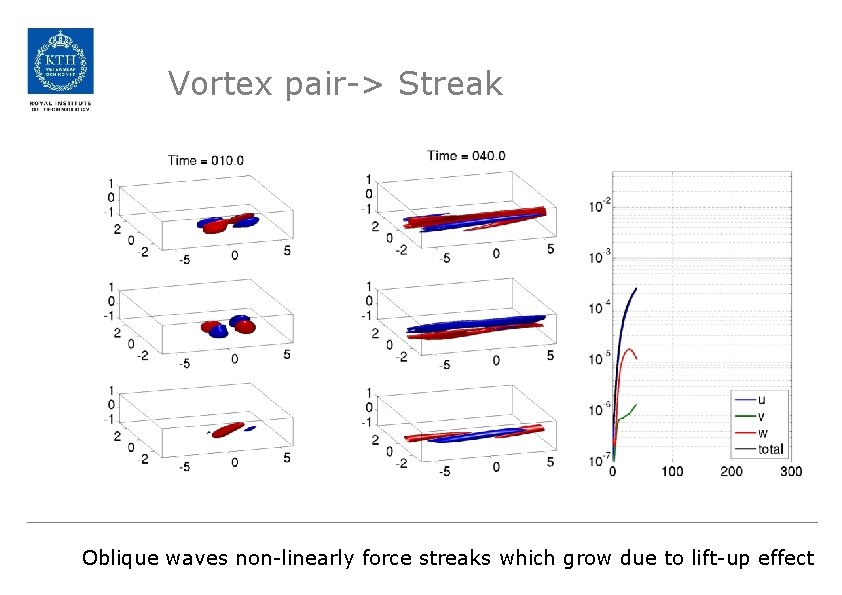
Vortex pair-> Streak Oblique waves non-linearly force streaks which grow due to lift-up effect

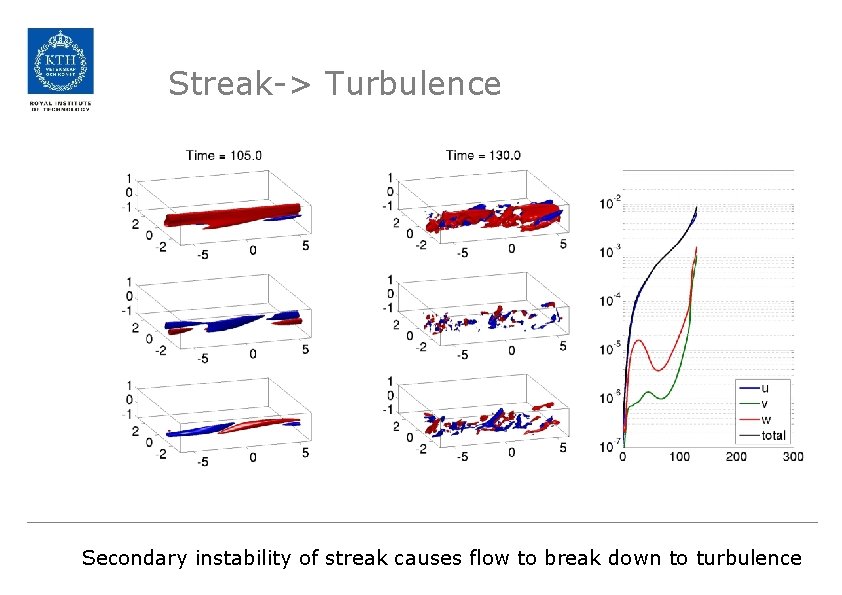
Streak-> Turbulence Secondary instability of streak causes flow to break down to turbulence

Comparison of the threshold values – Reddy, et al 1998 Monokrousos et all 2011 (Re=1500) – The numbers correspond to energy density of the initial disturbance – Significant reduction O(10) from the values relative to previous studies – Combination of several mechanisms to gain more energy (Orr, oblique forcing, lift-up, . . . )

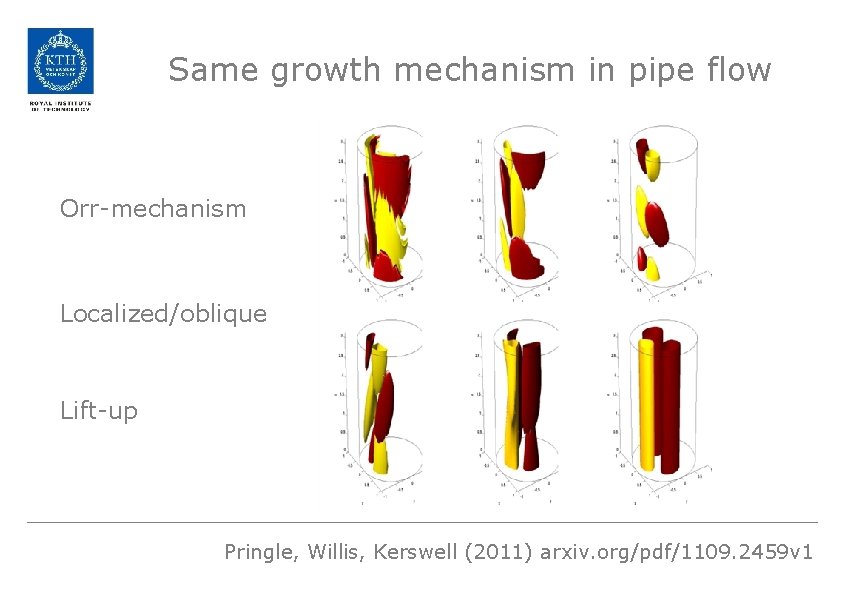
Same growth mechanism in pipe flow Orr-mechanism Localized/oblique Lift-up Pringle, Willis, Kerswell (2011) arxiv. org/pdf/1109. 2459 v 1

Conclusions – Non-linear optimization of turbulent flow using adjoints – Average viscous dissipation better choice than disturbance energy as objective function – Transition threshold reduced relative to previous studies – Fully localized optimal initial condition – Disturbance evolution utilizes combination of several growth mechanisms efficiently triggering turbulence (Orr, oblique, liftup) – Scenario general, also present in pipe flow

Thank you!

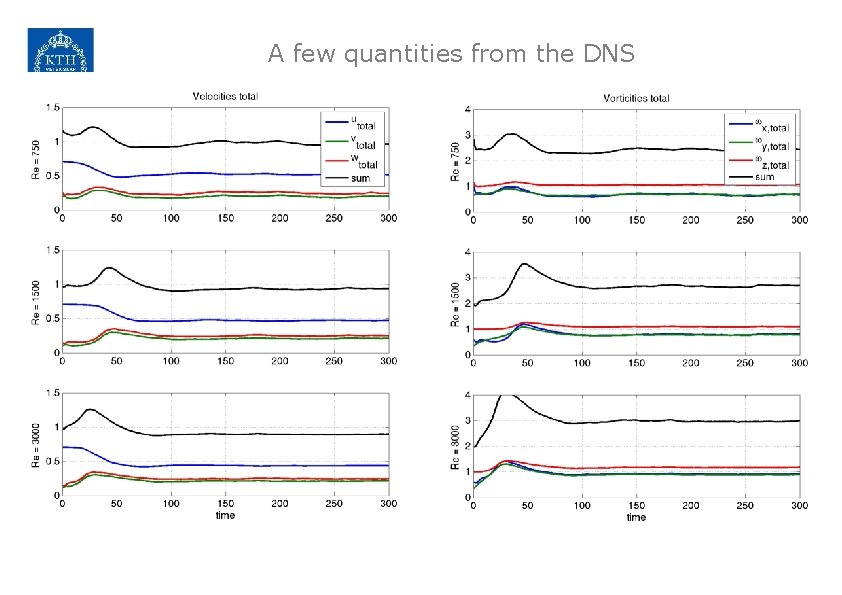
A few quantities from the DNS

Streak breakdown and oblique transition in channel flows

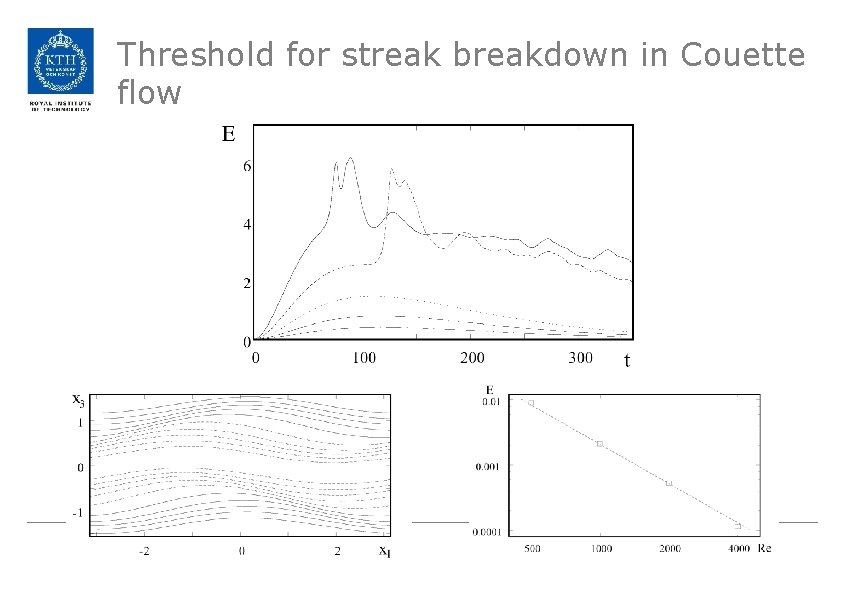
Threshold for streak breakdown in Couette flow

Nonlinear optimals and transition Linear optimals and weakly nonlinear approaches: vortices and streaks Suboptimal perturbations: oblique scenario (Viswanath & Cvitanovic 2010, Duguet et al. 2010) Nonlinear optimization: localized disturbances (Pringle & Kerswell, Cherubini et al. , ) Plane Couette flow: different box size and Re

Basic Formulation-Technique • State-space formulation – Define pressure through Poisson – Norm: – Define the adjoint operator: • Lagrange Function: – Find extrema of functional

Optimal initial condition Looking for the initial condition that maximizes the time integral of viscous dissipation • Governing equations and objective function Lagrange functional • Lagrange multipliers: and • Variations of the Lagrange function DNS of NS DNS of Adjoint NS Set the IC amplitude

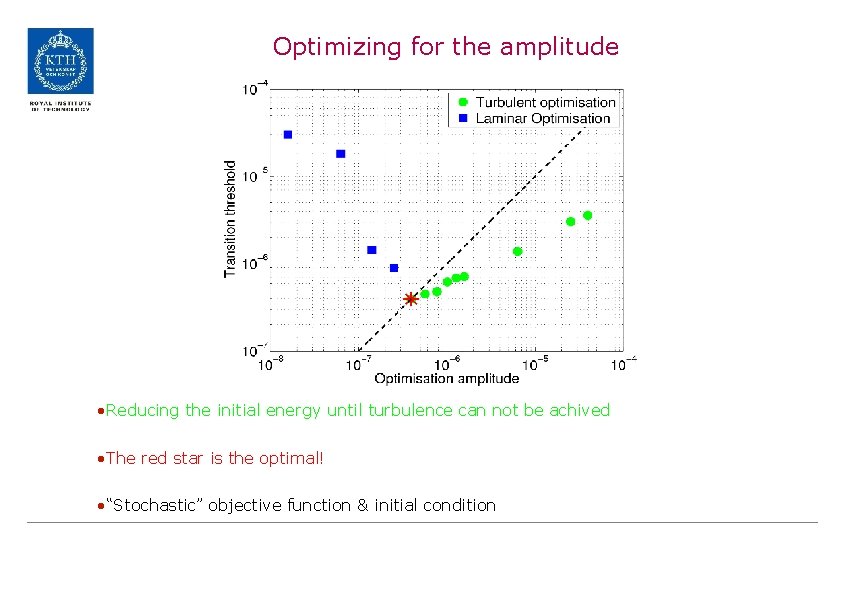
Optimizing for the amplitude • Reducing the initial energy until turbulence can not be achived • The red star is the optimal! • “Stochastic” objective function & initial condition

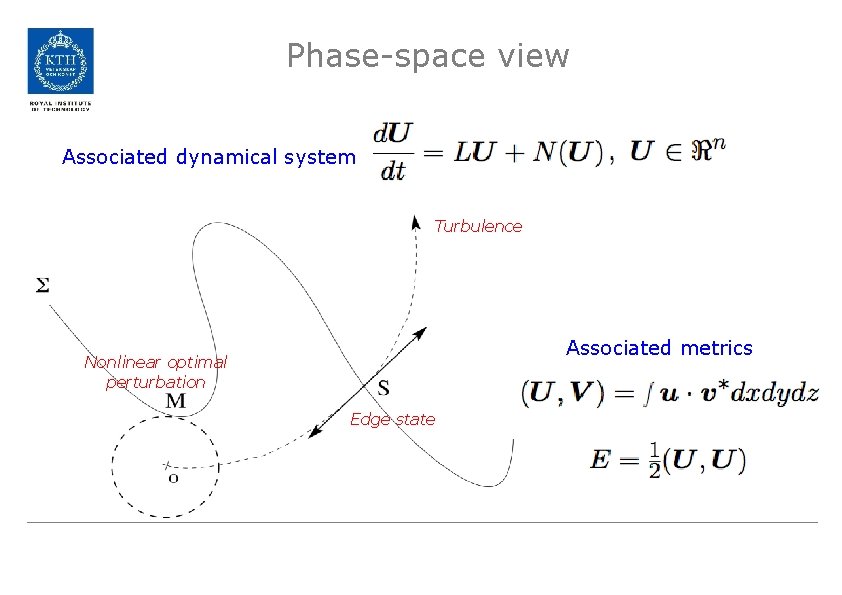
Phase-space view Associated dynamical system Turbulence Associated metrics Nonlinear optimal perturbation Edge state

Non-linear optimals and Transition • Optimization - Power iterations & Conjugate gradient - Time stepper • Different approaches - Linear optimals - Weakly non-linear (extension of the linear problem) - Fully non-linear (Turbulence) • Flow: Plane Couette